J. Cent. South Univ. Technol. (2010) 17: 635-641
DOI: 10.1007/s11771-010-0533-1 ![]()
Natural frequency of tapered high pier considering pile-soil interaction
ZHAO Ming-hua(赵明华), YANG Jing(杨晶), YANG Ming-hui(杨明辉)
Geotechnical Engineering Institute, Hunan University, Changsha 410082, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract:
In seismic design of tapered high pier, the analysis of natural vibration frequency is of great importance. According to the engineering features of tapered high pier in mountainous area, a vibration calculation model was set up considering the tapered pier characteristics and pile-soil interaction. Based on Southwell frequency composition theory, it consists of elastic deformation of bridge pier and the rigid deformation of group piles, which are respectively solved by the finite-element method and energy method, and then the natural frequency is derived. The comparison between the measured and calculated results shows that the calculation errors with and without considering pile-soil interaction are 4.9% and 14.7%, respectively. Additionally, the main parameters (pier height, section variation coefficient and lateral foundation horizontal proportional coefficient) affecting natural frequency were investigated. The result shows that natural frequency ascends with the increase of the lateral foundation horizontal proportional coefficient; and it is quite necessary to consider the pile-soil interaction in natural frequency calculation of tapered high pier.
Key words:
1 Introduction
Tapered high pier supported by pile group foundation is widely used for valleys or rivers in the particularly topographic and geological conditions in mountain areas, such as Longtan River Bridge of the Hu—Rong national highway [1]. So, in engineering field, it is significant to investigate the dynamic response properties of tapered high pier in seismic design [2]. Natural frequency, as an important dynamic property, must be reasonably calculated.
Presently, there are three common approaches for natural frequency calculation: (1) simple calculation model, (2) calculation according to standard empirical formulae, such as Railway and Bridge Checking Standard Rules, and (3) finite-element method or boundary element method [3-9]. CHEN [10] deduced natural frequency of pier by translating tapered high pier into a simple cantilever bar. This method is easy for calculation, but the result has a great error from actual value. The natural vibration formulae of high, middle pier, rock foundation and low pier are provided. But, the calculation module and data are not suitable for high pier with group foundation. LENG [11] adopted the equivalent section stiffness to do the three-dimensional space analysis, based on the assumption that the pile group foundation is one single pile. This method has a high accuracy in calculation. However, this complex method does not consider the pier nonlinearity and is limited to middle and low height pier with equal section. GAZETAS [12] presented a simplified calculation method of the pile group foundation in homogeneous soil, but it fails to take the soil-pile interaction into account. MAKRIS and GAZETAS [13] took the foundation as Winkler medium and perfected the simplified method mentioned above considering soil-pile interaction. However, it still fails to consider the linear variation of foundation spring.
Therefore, in order to consider the soil-pile interaction and pier geometry nonlinearity, a simplified calculation method was introduced. On this basis, the deep analysis of the related parameters was conducted, which was useful for high pier anti-seismic design.
2 Analysis model
As shown in Fig.1, the group piles were regarded as one single imaginary entity. And pile-soil interaction was investigated by “m” method.
As shown in Fig.2, the calculation width b(x) and length h(x) of the imaginary entity can be calculated as follows [14]:
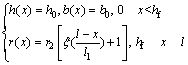
where b0 is the calculation width of the imaginary entity- end, and b0=u+2hftg(Ф/4); h0 is the calculation length of the imaginary entity-end, and h0=s+2hftg(Ф/4); s is the length of slab bottom pile planar contour; u is the width of

Fig.1 Calculation model of tapered high pier

Fig.2 Geometry dimension of calculation model
slab bottom pile planar contour; Ф is the average internal friction angle of soil layers where piles pass through; r(x) is the pier radius of x section, r(hf)=r1, r(l)=r2; and ξ is the circular section variation coefficient, ξ=(r1/r2)-1.
3 Calculation of vibration model
As shown in Fig.3, the calculation model was
decomposed into two parts: ω1 caused by the piles rigid rotation (cθ) and ω2 caused by the pier elastic deformation.
3.1 Calculation of ω1
Due to the fact that the rigid rotation cθ value is small in practical engineering, it satisfies: cθ=sincθ=tancθ. Then, the displacement function of pier can be expressed as follows when pile-end spring rotates:
![]() (1)
(1)
Let y1 be the pier top displacement, which satisfies the following equation: y1=cθl. According to the energy method [15-16], the maximum potential energy of pier can be calculated as follows:
![]() (2)
(2)
where ms is the average foundation proportional coefficient of soil layers where piles pass through; k1 is the rotational spring stiffness of imaginary entity end, which satisfies k1=m0I0 (where m0 is the foundation proportional coefficient of bottom soil; and I0 is the inertia moment of imaginary entity end).
When pier did the simple harmonic motion vibration at circular frequency of ω1, there is
![]() (3)
(3)
where φ is the initial phase.
The pier maximum kinetic energy T1 can be expressed as follows:
![]() (4)
(4)
where ρ1 is the average density of pier above ground or local scour level; ρ2 is the average density of imaginary entity foundation below ground, and A(x) is the area of x section.
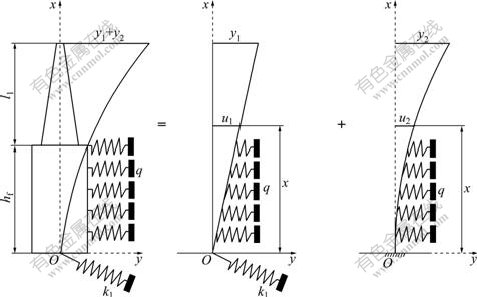
Fig.3 Decomposition of calculation model
According to the relation: V1=T1, by substituting Eq.(1) into Eq.(4), ω1 can be obtained from the following equations:
 (5)
(5)
where


3.2 Calculation of ω2
Due to the assumption of fixed pile-end, which satisfies y(0)=y′(0)=0, k1=0 (Fig.1). Let m(x) be the mass per unit length of arbitrary variable section, m(x)=ρA(x), and E2 the compound elastic modulus of imaginary entity foundation below ground, which satisfies E2=KpEp+ (1-Kp)Ep (where Kp is the foundation replacement ratio: Kp=npπd2/(4b0h0), d is diameter of single pile, and np is the roots number of piles).
According to Ref.[17], the free vibration differential formula can be determined from the following equations:
0≤x<hf
hf≤x<l
 (6)
(6)
where E1 is the elastic-modulus of piers above ground; I(x) is the inertia moment of x section; and ks(x) satisfies ks(x)=msb0(hf-x).
The solution of Eq.(4) is supposed to be as follows:
![]() (7)
(7)
By substituting Eq.(7) into Eq.(6), a simplified formula can be obtained:
0≤x<hf
hf≤x<l
 (8)
(8)
where A0 is the area of imaginary entity end.
Eq.(8) is a four-order variable differential equation set which has no exactly analytical solutions, thus the finite element method is employed to solve Eq.(8).
3.2.1 Element analysis
The ground lower part (hf) and ground upper part (l1) are respectively divided into n and m unites by equal space h. As shown in Fig.4, the local element i consists of two sections with arbitrary nodes i-1, i, i+1. While the value of h is low, the section area A(x) and inertia moment I(x) of element i of the ground upper part (l1) can be respectively estimated as follows: Ai=πr22[ξ(l1- ih)+l1]2/l12, Ii=πr24[ξ(l1-ih)+l1]4/(4l14); and correlated depth of element i of ground lower part (hf) was equal to (hf-ih). Then, Eq.(8) can be transformed into
0≤x<hf
hf≤x<l
 (9)
(9)
where
hf≤x<l, i=1,

0≤x<hf, i=1, 2, …, m
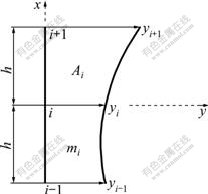
Fig.4 Displacement curve of element i
Because l1i and l2i of local element i are constants, general solution of Eq.(9) can be written as follows:
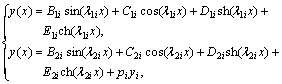 (10)
(10)
where pi=di/λ2i4.
Calculating the derivative of Eq.(10) with respect to x, then:
![]()
![]() (11)
(11)
By means of the element boundary condition, we can obtain: while x=-h, node i-1 satisfies y(x)=yi-1, ![]() while x=h, node i+1 satisfies y(x)=yi+1,
while x=h, node i+1 satisfies y(x)=yi+1, ![]() Then,
Then,
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
where a1,2i=λ1,2ih; and constants of B1,2i, C1,2i, D1,2i, E1,2i are the functions of λ1,2i.
3.2.2 Basic form of element equation
Substituting x=0 into Eqs.(10) and (11), the following equations can be obtained:
![]() (18)
(18)
and
![]() (19)
(19)
B1,2i, C1,2i, D1,2i, E1,2i are substituted into Eqs.(18) and (19), then through transposition of terms, Eqs.(18) and (19) can be written as follows:
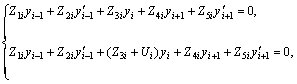 (20)
(20)
and
![]() (21)
(21)
where
Z1i=λ1,2i[(cosa1,2i+sina1,2itha1,2i)tana1,2i+(sha1,2i +
cha1,2i tana1,2i)tha1,2i];
Z2i=(sha1,2i-cosa1,2i)+(cha1,2itana1,2i-sina1,2itha1,2i);
Z3i=-2λ1,2i(sha1,2i +cha1,2i tana1,2i)?
(cosa1,2i +sina1,2i tha1,2i);
Z4i=Z1i; Z5i=-Z3i;
Ui=-pi{Z3i+2λ2i[tana2i (cosa2i+sina2itha2i)+ tha2i (sha2i+
cha2itana2i)]};
W1i=λ1,2i[(cosa1,2i-sina1,2itha1,2i)cota1,2i+(cha1,2i-
sha1,2icota1,2i)ctha1,2i];
W2i=(cha1,2i+cosa1,2i)-(sha1,2icota1,2i+sina1,2ictha1,2i);
W3i=-2(cha1,2i-sha1,2icota1,2i)(cosa1,2i-sina1,2ictha1,2i);
W4i=-W1i; W5i=W2i; and a1,2i=λ1,2ih.
Eqs.(20) and (21) are linear relations respectively about displacement and rotation angle of node i. They are all the functions of λ1,2i.
3.2.3 Boundary condition and continuity conditions of x=hf
(1) Continuity conditions of x=hf (as shown in Fig.5)
For ground lower part (hf), the corresponding analysis element is the mth unit (di=0). While x=-h, it?satisfies y(x)=ym-1, y′(x)=y′m-1; while x=0, it satisfies y(x)=ym, y′(x)=y′m.
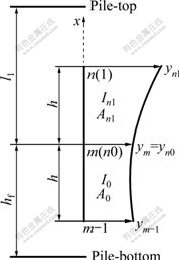
Fig.5 Element analysis at height hf
Simultaneously calculating with Eqs.(10), (11), (20) and (21), then the following equations will be obtained:

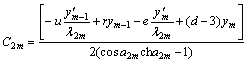
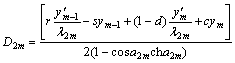

where r=cha2m-cosa2m; s=sha2m+sina2m; u=sha2m-sina2m; v=sina2msha2m+cosa2mcha2m; c=cosa2msha2m+sina2mcha2m; d=cosa2mcha2m-sina2msha2m; e=sina2mcha2m-cosa2msha2m; and a2m=-λ2mh.
Therefore, B2m, C2m, D2m and E2m can be calculated by ym-1, y′m-1, ym and y′m.
For the ground upper part (l1), the corresponding analysis element is the first unit (di=0). While x=0, it satisfies y(x)=yn0, y′(x)=y′n0; while x=h, it satisfies y(x)= yn1, y′(x)=y′n1.
By simultaneously calculating Eqs. (10), (11), (20) and (21), B1,n0, C1,n0, D1,n0, E1,n0 can also be calculated by yn1, y′n1, yn0 and y′n0 (a1,n0=λ1,n0h).
While x=hf, according to the general solution forms, the displacement curve is smooth and continuous, and approximately satisfies ![]() and
and![]() Therefore, the following equations can be obtained while x=0:
Therefore, the following equations can be obtained while x=0:
![]() (22)
(22)
![]() (23)
(23)
By substituting expressions of B2m, C2m, D2m, E2m ; B1,n0, C1,n0, D1,n0, E1,n0 into Eqs.(22) and (23), two linear formulas about ym and y′m (or yn0 and y′n0) can be derived.
(2) Fixation pile tips
Because of the fixation of pile tips, there exists y0=![]() =0.
=0.
(3) Cantilever end
For cantilever end (x=l), moment and shear force are both zero, namely, ![]()
3.2.4 Solution of ω2
Summarizing above equations, non-boundary-nodes displacement expressions of tapered high pier can be derived, which are similar to the displacement of Eqs.(20) and (21). Meanwhile, with considering the boundary conditions and continuity condition at x=hf, the 2(m+n) linear equations can be written on matrix forms as follows:
[K]{Y}2(m+n)={0} (24)
where [K] is 2(m+n)×2(m+n) order matrix, all of which only contain one unknown variable ω2; {Y}2(m+n)= ![]() …,
…, ![]() …, ynn,
…, ynn, ![]() is the generalized matrix of displacement. And when the pier carries the self-vibration, it is not constant for zero, thus matrix [K] must satisfy the following equation:
is the generalized matrix of displacement. And when the pier carries the self-vibration, it is not constant for zero, thus matrix [K] must satisfy the following equation:
|[K]|=0 (25)
Through the solution of Eq.(25), ω2 can be obtained.
3.3 Calculation of compound natural frequency ω
According to the Southwell frequency composition methods [18], the lower limit of compound frequency ω can be calculated as follows:
![]() ≤ω (26)
≤ω (26)
Therefore, summarizing the whole solution, the value of compound frequency w is affected by the following parameters: E1, Ep, Es, np, d; ms, m0, ξ, h, r1, r2; l1, ρ1, ρ2, b0, h0, hf.
4 Engineering application
4.1 Calculation example 1
Taking one pier of a certain bridge of Jiaozhi—Zhiliu railway for engineering calculation (detailed size information is shown in Fig.6) [19], which is circular pier with group piles foundation (four circular piles with pile length of 20 m, pile diameter of 0.76 m and the pile space of 2.76 m×2.76 m). The pier body material uses C15 slabstone concrete (unit weight is 24 kN/m3 and Ep is 2.06×104 MPa). Pallet and top cap use C18 concrete (unit weight is 26 kN/m3 and Ep is 2.4×104 MPa). Dimension of platform is 4.8 m×4.8 m×1.5 m, which uses C18 concrete. The average unit weight of foundation soil (Es is 15 MPa) is 20 kN/m3 and the internal friction angle is 18?.

Fig.6 Dimension of pier and calculation model
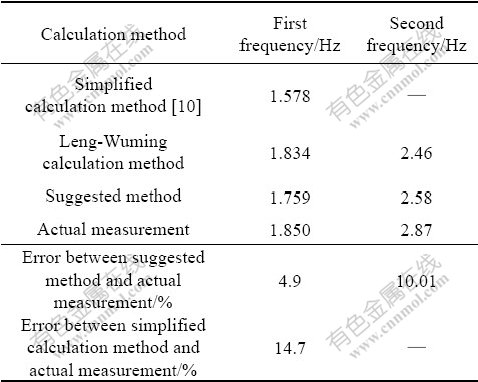
According to Specifications for Design of Ground Base and Foundation of Highway Bridges and Culverts, the dimensions of imaginary entity foundation are 6.144 m×6.144 m×21.5 m; ms=3 000 kN/m4; and m0= 1×104 kN/m3. Let equal space h be 0.5 m. With the relevant Matlab programs worked out, the calculation results can be obtained, which are shown in Table 1.
Table 1 indicates that simplified calculation method in Ref.[10] is easy; and the calculation result has great difference from measured values. The Leng-Wuming calculation method can obtain the results close to measured values and suggested calculation results, but the calculation process is very complex and it cannot take the nonlinearity of pier body into account. It is obvious that the calculation approach suggested in this work is more practical and more accurate.
4.1 Calculation example 2
The No.12 pier of Lan river bridge of Beijing—
Table 1 Results of frequency calculation
Qinhuangdao railway is taken for engineering calculation, which is circular pier with group piles foundation (eight circular piles with pile length of 21.13 m and pile diameter of 1.55 m; distribution form is 2×4; and Ep is 2.9×104 MPa). Foundation soil consists of 2 layers: the upper layer is land pebble with thickness of 18.67 m (internal friction angle 28?; unit weight 25 kN/m3; Es 15 MPa; and ms 5×104 kN/m4); the lower layer is base rock (m0 1.2×105 kN/m3); and the pile tip socketed depth is 2.46 m. The height of pier cap from platform bottom is 18.5 m; the elastic modulus of pier body is 2.4×104 MPa; and the inertia moment I of cross section is 184.48 m4.
As for ω1, by substituting the above data into Eq.(5), we can obtain the value of ω1, which is 28.592 6 rad/s. Due to the non-variable section of pier body, the equal space h1 of pier body is taken as 18.5 m; simultaneously, the equal space h2 of piles group (imaginary entity foundation) is taken as 1.5 m. According to Eq.(25), the solution of ω2 is 17.73 rad/s. And then the compound frequency ω can be calculated by Eq.(26), which is 2.398 3 Hz. The actually measured frequency is 2.2 Hz. An error of 9.01% indicates that the suggested calculation result is consistent with the actual measurement. While according to the calculation equation of Test Specification of Railway Bridge, the minimum relevant limit value of pier frequency fz0 is 4.7 Hz, which has a great deviation from the actual measured value.
In order to analyze the influence of the prime parameters on structure natural frequency, the first engineering example is taken as calculation mode.
5.1 Effect of section variation coefficient
Fig.7 shows the curve of section variation coefficient ξ vs natural frequency at a certain pier height. From Fig.7, it can be seen that natural frequency slightly decreases with the increases of section variation coefficient ξ, while keeping the sum of r2 and r1 unchanged.

Fig.7 Curve of section variation coefficient ξ vs natural frequency
5.2 Effect of pile lateral foundation horizontal proportional coefficient
Fig.8 shows the curve of pile lateral foundation horizontal proportional coefficient ms vs natural frequency, which presents that natural frequency increases with the increase of ms. According to the principle of energy conservation, the maximum vibration system potential energy ascends with the increase of the maximum kinetic energy, which is caused by the increase of ms.

Fig.8 Curve of pile lateral horizontal proportional coefficient ms vs natural frequency
5.3 Effect of pier height l1
Fig.9 describes the curve of height of pier vs natural frequency while keeping r2 and r1 invariant, which represents the gradual decrease of natural frequency with the increase of pier height. With the reduction of structural stiffness and the increases of structural weight when the pier height grows, the natural frequency of pier decreases.
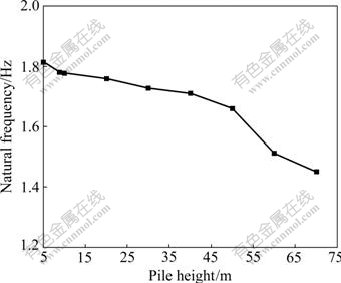
Fig.9 Curve of pier height vs natural frequency
6 Conclusions
(1) By simplifying group piles foundation of tapered high pier into a single entity foundation and considering soil-pile interactions by “m” method, a simple self- vibration model is established. According to the Southwell frequency composition theory, the vibration model is decomposed into two parts: the rigid rotation model of piles and elastic deformation model of pier respectively solved by the energy method and finite- element method.
(2) The engineering calculation results demonstrate that the suggested calculation methods can be applied to natural frequency solution of engineering high pier. And compared with the known methods, more influencing factors are taken into account.
(3) Section variation coefficient, ξ , has little effect on natural frequency of pier at a certain height. Natural frequency gradually decreases with the increases of pier height. However, natural frequency ascends dramatically with the increase of pile lateral horizontal proportional coefficient, which suggests that soil-pile interaction cannot be neglected in dynamic calculation of tapered high pier.
References
[1] LUO Yu-ke, FENG Peng-cheng. Design of Longtanhe river bridge [J]. Bridge Construction, 2005(2): 29-32. (in Chinese)
[2] WANG Ke-hai, LI Qian. Analysis of seismic response of bridges with high rise piers [J]. World Bridges, 2006(1): 29-32. (in Chinese)
[3] KAYNIA A M, KAUSEL E. Dynamic stiffness and seismic response of pile groups [R]. R82-03, Massachusetts Institute of Technology, 1982.
[4] POULOS H G. Analysis of the settlement of pile groups [J]. Geotechnique, 1988, 38(4): 449-471.
[5] MAMOON S M, KAYNIA A M, BANERJEE P K. Frequency- domain dynamic analysis of piles and pile groups [J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1990, 116(10): 2273-2257.
[6] SEN R, DAVIS G, BANERJEE P K. Dynamic analysis of piles and pile groups embedded in homogeneous soils [J]. Earthquake Engng Struction Dyn, 1985, 13: 53-65.
[7] JU S H. Three-dimension analysis of wave barriers for reduction of train-induced vibration [J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2004, 130(7): 740-748.
[8] ANDRSEN L, NIELSEN S R K. Reduction of ground vibration by means of barriers or soil improvement along a railway track [J]. Soil Dynamic and Earthquake Engineering, 2005, 25(7): 701-716.
[9] YAU J D, YANG Y B. Vibration reduction forcable stayed bridges traveled by high-speed trains [J]. Finite Element in Analysis and Design, 2004, 40: 341-359.
[10] CHEN Xing-chong. Formulae of energy method for the natural frequency of brigde piers [J]. China Civil Engineering Journal, 1999, 32(5): 76-80. (in Chinese)
[11] LENG Wu-ming. Study on natural frequency of bridge pier supported by group pile foundation [J]. Journal of the China Railway Society, 1999, 21(4): 72-76. (in Chinese)
[12] GAZETAS D R. Simple method for dynamic stiffness and damping of floating pile groups [J]. Geotechnique, 1988, 38(4): 557-574.
[13] MAKRIS N, GAZETAS G. Dynamic pile soil pile interaction (Part II): Lateral and seismic response [J]. Earthquake Energy Struct Dyn, 1992, 21(2): 145-162.
[14] The Professional Standards Compilation Group of People’s Republic of China. Specifications for Design of Ground Base and Foundation of Highway Bridges and Culverts (JTJ024-85) [S]. Beijing: China Communications Press, 1985. (in Chinese)
[15] GROSSI R O, AIBARRACIN C M. Some observations on the application of the Rayleigh-Ritz method [J]. Applied Acoustics, 2001(62): 1171-1182.
[16] BAI Qing-xia, SONG Yi-fan. Energy method for the geometric non-linear analysis of higher bridge piers [J]. Journal of Xi’an Highway Transportation University, 2001, 21(2): 50-52. (in Chinese)
[17] ZHANG Rong-shan. Engineering vibration and control [M]. Beijing: China Architecture Industry Press, 2003. (in Chinese)
[18] NALLIM L G, GROSSI R O. A general algorithm for the study of dynamical behavior of beams [J]. Applied Acoustics, 1999(57): 345-356.
[19] ZHOU Hai-lin, LENG Wu-ming. Computation of dynamic behavior of bridge pier supported by group pile [J]. China Railway Science, 2001, 22(3): 51-56. (in Chinese)
Foundation item: Project(50708033) supported by the National Natural Science Foundation of China
Received date: 2009-06-17; Accepted date: 2009-10-19
Corresponding author: ZHAO Ming-hua, PhD, Professor; Tel: +86-731-88821590; E-mail: mhzhaohd@21cn.com
(Edited by YANG Bing)
Abstract: In seismic design of tapered high pier, the analysis of natural vibration frequency is of great importance. According to the engineering features of tapered high pier in mountainous area, a vibration calculation model was set up considering the tapered pier characteristics and pile-soil interaction. Based on Southwell frequency composition theory, it consists of elastic deformation of bridge pier and the rigid deformation of group piles, which are respectively solved by the finite-element method and energy method, and then the natural frequency is derived. The comparison between the measured and calculated results shows that the calculation errors with and without considering pile-soil interaction are 4.9% and 14.7%, respectively. Additionally, the main parameters (pier height, section variation coefficient and lateral foundation horizontal proportional coefficient) affecting natural frequency were investigated. The result shows that natural frequency ascends with the increase of the lateral foundation horizontal proportional coefficient; and it is quite necessary to consider the pile-soil interaction in natural frequency calculation of tapered high pier.


