
J. Cent. South Univ. (2018) 25: 169-184
DOI: https://doi.org/10.1007/s11771-018-3727-6

Asymmetric Green’s functions for exponentially graded transversely isotropic substrate–coating system
F. Akbari1, A. Khojasteh2, M. Rahimian1
1. School of Civil Engineering, College of Engineering, University of Tehran, Tehran 11155-4563, Iran;
2. School of Engineering Science, College of Engineering, University of Tehran, Tehran 11155-4563, Iran
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract:
By virtue of a complete set of two displacement potentials, an analytical derivation of the elastostatic Green’s functions of an exponentially graded transversely isotropic substrate–coating system is presented. Three-dimensional point–load and patch–load Green’s functions for stresses and displacements are given in line-integral representations. The formulation includes a complete set of transformed stress–potential and displacement–potential relations, with utilizing Fourier series and Hankel transforms. As illustrations, the present Green’s functions are degenerated to the special cases such as an exponentially graded half-space and a homogeneous two-layered half-space Green’s functions. Because of complicated integrand functions, the integrals are evaluated numerically and for numerical computation of the integrals, a robust and effective methodology is laid out which gives the necessary account of the presence of singularities of integration. Comparisons of the existing numerical solutions for homogeneous two-layered isotropic and transversely isotropic half-spaces are made to confirm the accuracy of the present solutions. Some typical numerical examples are also given to show the general features of the exponentially graded two-layered half-space Green’s functions that the effect of degree of variation of material properties will be recognized.
Key words:
Cite this article as:
F. Akbari, A. Khojasteh, M. Rahimian. Asymmetric Green’s functions for exponentially graded transversely isotropic substrate–coating system [J]. Journal of Central South University, 2018, 25(1): 169–184.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-018-3727-61 Introduction
Continuously varying mechanical characteristics of functionally graded composite materials have broad application in industrial engineering including thermal barriers, abradable seals, wear-resistant and oxidation resistant coatings due to better residual stress distribution, thermal properties and greater fracture toughness. This advantage eliminates the interface problems of traditional laminated composites and therefore the stress distribution will be continuous and smooth [1]. Also, functionally graded materials (FGMs) having the desired variation of material properties in spatial directions are widely used in different applications such as aerospace and automobile industries [2]. It is important to note that in some cases, before trying to produce such materials for specific application, the applicability and efficiency of such special variation should be examined through exact theoretical and numerical schemes.
KIEBACK et al [3] discussed the processing scheme by SOBCZAK and DRENCHEV [4] and investigated the production methods mainly for metal based FGMs and the experimental and theoretical estimation of graded properties by. Also, for the experimental and theoretical investigations of the calculation and predication of material properties of functionally graded materials, one might refer to CHO and ODEN [5], HORI and NEMAT-NASSER [6], RAHMAN and CHAKRABORTY [7]. For an inclusive review of the recent developments in the theory and application of FGMs and the subjects of further research, one might refer to BIRMAN and BYRD [8]. In addition to manufactured functionally graded composite materials, the deeper understanding of the deposited soil and rock formations have attracted researchers to the area of analysis of stress transfer in this type of materials and utilization of their advantages. It is noteworthy that in the formwork of classical elasticity, the exponential relation would simplify the mathematical formulation. The assumption of exponential transition function for the material properties of the medium has been employed in several studies. This assumption is widely used for FGMs in the engineering literature [9].
WANG et al [10] presented the problem of an exponentially graded transversely half-space subjected to a uniform vertical circular load. MARTIN et al [9] presented a Green’s function of three-dimensional exponentially graded elastic isotropic solids. CHAN et al [11] presented general analytical technique for obtaining the Green’s function for two-dimensional exponentially graded elastic isotropic solids. KASHATALYAN and RUSHCHITSKY [12] presented a displacement function in three-dimensional elasticity of transversely isotropic inhomogeneous media with assuming constant Poisson ratio and functionally graded elastic and shear moduli. SALLAH et al [13] obtained the Green’s function for three-dimensional exponentially graded elasticity. ESKANDARI and SHODJA [2] derived an exponentially graded transversely isotropic half-space Green’s functions. ESKANDARI- GHADI and AMIRI-HEZAVEH [14] presented the wave propagations in exponentially graded transversely isotropic half-space with potential function method with the aid of Fourier series and Hankel transform. KATEBI and SELVADURAI [15] examined the axisymmetric interior loading problem for an incompressible isotropic elastic half-space where the linear elastic shear modulus varies exponentially with depth.
On the other hand, nowadays, coatings are used to modify surface properties of engineering materials and components [16]. In other situations, due to corrosion, polishing, and chemical reactions, the material properties of thin layer on the surface of half-space may be completely altered, resulting in a two-phase material [17]. Pavements, slabs on grounds, and mat foundations are known as the classical example of coating application in civil engineering. Therefore, analysis of a coating- substrate system with dissimilar material properties is also of practical interest to material scientists. The degree of complexity of the problem depends on the material properties of the layers, number, nature of the interfacial conditions and loading conditions, and the degree of the material inhomogeneity, among other factors.
There are plenty of works in the literature dealing with the problems of an isotropic coating-substrate subjected to surface or buried loads. Apart from the isotropic materials, the static and dynamic response of anisotropic materials is of major concern because of high performance in the technological application. Most innovative, smart, and intelligent materials such as composites, piezomagnetics, and piezoelecterics are anisotropic, and in application they are often modeled as transversely isotropic or orthotropic materials. RAHMAN and NEWAZ [17] considered the surface displacement of a transversely isotropic half-space with a thin-film coating layer under static surface loading. SHODJA and ESKANDARI [18] derived the axisymmetric time-harmonic response of a coated transversely isotropic half- space by means of three potential functions. KHOJASTEH et al [19] presented elastodynamic Green’s functions for a transversely isotropic layer underlain by a transversely isotropic half-space under point-loads and patch loads. KHOJASTEH et al [20, 21] derived three-dimensional Green’s functions in a transversely isotropic bi-material full- space and tri-material full-space. PAN and YANG [22] derived three-dimensional static interfacial Green’s functions in anisotropic bi-materials. ESKANDARI-GHADI et al [23] presented the dynamic response of a transversely isotropic, linearly elastic layer bonded to the surface of a half-space of a different transversely isotropic material under surface loads. KHOJASTEH et al [24] presented an efficient and accurate analytical derivation of three-dimensional dynamic Green’s functions for a transversely isotropic multi-layered half-space with the aid of displacement potential method. ESKANDARI and AHMADI [25] derived Green’s functions of a transversely isotropic half- space overlaid by a thin coating layer and the surface coating is modeled by a Kirchhoff thin plate perfectly bonded to the half-space. The existing works in this area related to anisotropic FGM materials are very limited.
Green’s function is the key solution for many problems in linear elasticity, applied and theoretical studies on the physics on solids, and various numerical methods based on the integral-equation- formulation such as the well-known boundary element method. Green’s functions are the foundation of further works.
In this work the, Green’s function of an exponentially graded transversely isotropic two- layered half-space is presented. To this end, the potential method presented by RAHIMIAN et al [26] for transversely isotropic and new displacement potentials presented by ESKANDARI-GHADI and AMIRI-HEZAVEH [14] are utilized. An arbitrary point load or patch-load is assumed to be applied at surface or interface of two media. The formulation includes a complete set of transformed stress–potential and displacement–potential relations, with utilizing Fourier series and Hankel transforms. The complete set of point-load and patch-load Green’s functions of displacements and stresses are given in terms of line-integral representations. The elastic constants of materials are assumed varying exponentially along the axis of symmetry of the solid. The formulation and numerical implementation are examined and verified by comparisons of their degenerate forms to some benchmark solution such as static Green’s functions for a two-layered transversely isotropic half-space. The effect of material inhomogeneity is elucidated by several numerical displays. Green’s functions presented in this paper are of great value in developing boundary-integral- equation for analysis of soil-structure interaction and composites relevant problems.
2 Governing equations in displacement potentials
The governing equilibrium equations for a vertically heterogeneous transversely isotropic elastic solid which its material properties vary exponentially along the axis of symmetry of the solid, in terms of displacements and in the absence of the body forces can be expressed as [26]

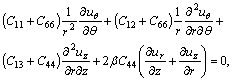
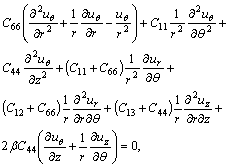
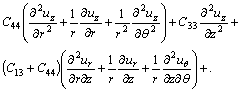
 (1)
(1)
in a cylindrical coordinate system (r, θ, z); where z-axis is the axis of symmetry of the solid, ur, uθ and uz are the displacement components in the r, θ and z directions, respectively; Cij are elasticity constants of the solid whit C66=(C11–C12)/2; and β is the exponential factor characterizing the degree of material gradient in the z-direction. Here, it is assumed that the elastic constants of the medium vary exponentially in the z-direction as
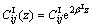 (2)
(2)
in medium Ⅰ, and
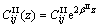 (3)
(3)
in medium Ⅱ, where 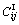 and
and 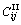 indicate the z-independent elastic constant corresponding to the surface of each layer. It is obvious that β=0 corresponds to the homogeneous transversely isotropic two-layered half-space. In order to solve the coupled partial differential Eq. (1), a set of complete potential functions F and χ introduced by ESKANDARI- GHADI and AMIRI-HEZAVEH [14] is used. These two potential functions are related to displacement components, ur, uθ and uz as follows:
indicate the z-independent elastic constant corresponding to the surface of each layer. It is obvious that β=0 corresponds to the homogeneous transversely isotropic two-layered half-space. In order to solve the coupled partial differential Eq. (1), a set of complete potential functions F and χ introduced by ESKANDARI- GHADI and AMIRI-HEZAVEH [14] is used. These two potential functions are related to displacement components, ur, uθ and uz as follows:
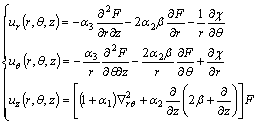 (4)
(4)
where
 (5)
(5)
and
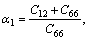
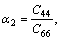
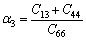 (6)
(6)
Substituting Eq. (4) into Eq. (1) results in two separate partial differential equations (PDEs) as the governing equations for potential function F and χ:
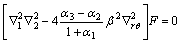 (7)
(7)
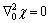 (8)
(8)
where
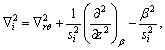 i=0, 1, 2 (9)
i=0, 1, 2 (9)
 (10)
(10)
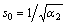 and s1 and s2 are the roots of the following equation which in view of the positive- definiteness of the strain energy are not zero or pure imaginary numbers [27].
and s1 and s2 are the roots of the following equation which in view of the positive- definiteness of the strain energy are not zero or pure imaginary numbers [27].
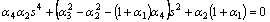 (11)
(11)
By virtue of Fourier expansion with respect to the angular coordinate θ, one may express [28]
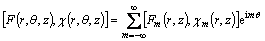 (12)
(12)
with similar expressions for the displacement and stress components. Moreover, utilizing the mth order Hankel transform pair sufficiently regular function f(r, z) with respect to the radial coordinate as [29]
 (13)
(13)
the following ordinary differential equations for F and χ can be obtained:
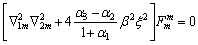 (14)
(14)
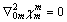 (15)
(15)
where
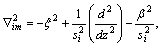 i=0, 1, 2 (16)
i=0, 1, 2 (16)
The general solution of Eqs. (14) and (15) can be written as
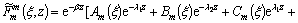
 (17)
(17)
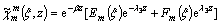 (18)
(18)
where
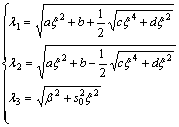 (19)
(19)
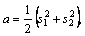
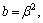
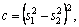
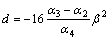 (20)
(20)
and Am, …, Fm are constants of integration to be determined from boundary conditions. The values of λ1, λ2 and λ3 are selected in such a way that Re(λj)≥|β| satisfies radiation conditions.
By means of Eq. (4) and the identities involving Hankel transforms, the transformed displacement-potential relations may expressed compactly as follows:
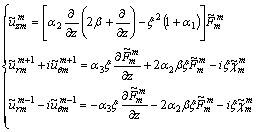 (21)
(21)
while the transformed stress-potential relationships can be written as follows:


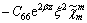 (22)
(22)
With the aid of Eqs. (17), (18), (20) and (22), the imposition of the loading, interfacial and regularity conditions associated with a two-layered FGM is greatly facilitated, as will be illustrated in the ensuing sections.
3 Statement of problem
A two-layered FGM system is shown in Figure 1, composed of an exponentially graded transversely isotropic elastic layer of arbitrary thickness h perfectly bonded to an exponentially graded transversely isotropic half-space of another transversely isotropic material, along their common interface. Figure 1 depicts a cylindrical coordinate system (r, θ, z) in such a way that z-axis is normal to the horizontal interface of the domain, and so it is the common axis of symmetry of both media. Let the upper layer (0<>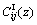 and the ones of the lower layer (referred to as medium Ⅱ) as
and the ones of the lower layer (referred to as medium Ⅱ) as 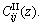 Hereafter, the superscripts Ⅰ and Ⅱ denote the quantities in media Ⅰ and Ⅱ, respectively. Applying an arbitrary traction on a finite region
Hereafter, the superscripts Ⅰ and Ⅱ denote the quantities in media Ⅰ and Ⅱ, respectively. Applying an arbitrary traction on a finite region 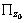 which is located at depth z=z0, z0=0 or h, gives the traction boundary conditions as follows:
which is located at depth z=z0, z0=0 or h, gives the traction boundary conditions as follows:
 (23-1)
(23-1)

Figure 1 Functionally graded transversely isotropic substrate-coating system under arbitrary load
when the load is applied at the surface and
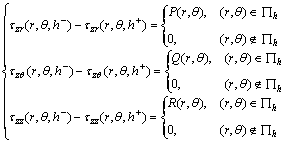 (23-2)
(23-2)
when the load is applied at the interface where P(r, θ), Q(r, θ) and R(r, θ) are the specified interfacial traction distributions in radial, angular, and axial directions, respectively. Consistent with the regularity condition at infinity the general solutions (17) and (18) for F and χ can be rearranged as
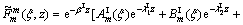
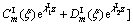 (24)
(24)
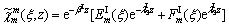 (25)
(25)
in medium Ⅰ, and
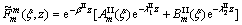 (26)
(26)
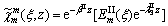 (27)
(27)
in medium Ⅱ. In the above,  …,
…,  are the integration constants to be determined using the boundary conditions. The
are the integration constants to be determined using the boundary conditions. The 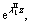
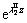 and
and 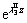 terms in medium II become inadmissible due to radiation conditions and are thus omitted. For the general exponentially graded two-layered half- space problem of interest, an exact solution therefor requires the determination of nine coefficients. With the aid of Eqs. (21) and (22), interfacial traction conditions (23) together with the continuity of displacements across the plane z=h provide nine equations required for the solution of the nine unknown coefficients
terms in medium II become inadmissible due to radiation conditions and are thus omitted. For the general exponentially graded two-layered half- space problem of interest, an exact solution therefor requires the determination of nine coefficients. With the aid of Eqs. (21) and (22), interfacial traction conditions (23) together with the continuity of displacements across the plane z=h provide nine equations required for the solution of the nine unknown coefficients  …,
…,  as follows:
as follows:
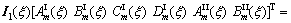
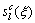 (28)
(28)
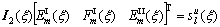 (29)
(29)
where
 (30)
(30)
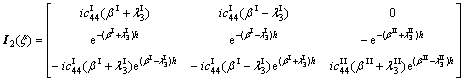 (31)
(31)
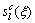 and
and  are source vectors given by
are source vectors given by
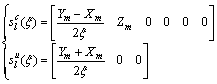 (32)
(32)
when the load is applied at the surface and
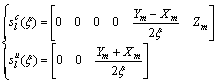 (33)
(33)
when the load is applied at the interface.
Here
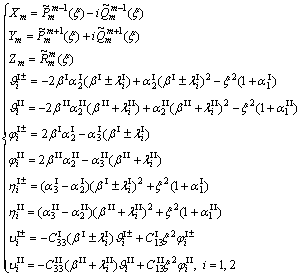 (34)
(34)
In expressions (28)–(31), Cij are the piecewise constant elastic moduli given by
 (35)
(35)
upon setting βI=βII=0. The above equations lead exactly to the one proposed by KHOJASTEH et al [19] for the homogeneous case in the static condition.
On substituting the inverted Fourier components of the displacements and stresses into the corresponding angular eigenfunction expansion, the desired formal solution to the general exponentially graded two-layered half-space problem under consideration can be obtained.
4 Point-load Green’s function
In the preceding sections, the general solution has been formulated for an arbitrary source distributed on the plane z=z0. To obtain the point-load Green’s functions, which are useful for integral formulations of boundary value problems, one may define the distributed traction source as [19]
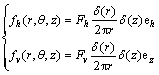 (36)
(36)
in the horizontal and vertical directions, respectively, where δ is the one-dimensional Dirac delta function; eh is the unit horizontal vector in the θ=θ0 direction given by
 (37)
(37)
(see Figure 2); er, eθ and ez are the unit vectors in the radial, angular, and vertical directions, respectively; and Fh and Fv are the point-load magnitudes. By virtue of the angular expansions of the stress discontinuities across the plane z=z0 and the orthogonality of the angular eigenfunctions 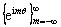 , one finds
, one finds
 (38)
(38)
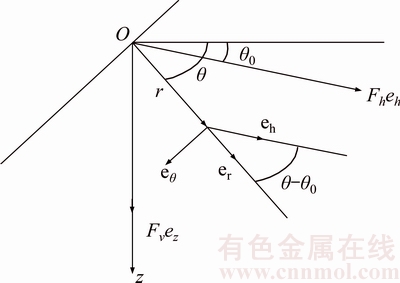
Figure 2 Vertical and horizontal point-load configurations
for the point-load in Eq. (36). Subsequently, the transformed loading coefficients Xm, Ym and Zm can be expressed as [20]
 (39)
(39)
Upon inverting the transformed expressions (20) and (21) and using (39), the displacement and stress point-load Green’s functions may be written as

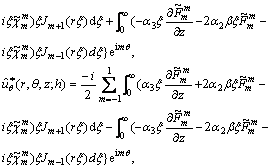
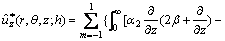
 (40)
(40)
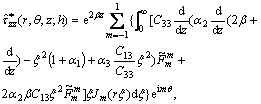

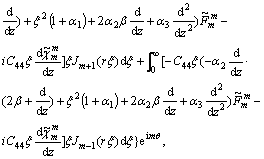
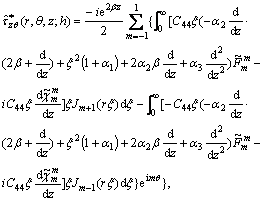

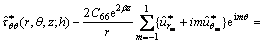

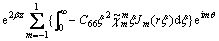 (41)
(41)
In the above, the symbols “ ” and “
” and “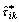 ” (i, k=r, θ, z) denote, respectively, the displacement and stress Green’s function, with the superscript “*” denoting the direction of the point-load upon appropriate specifications of Fh, Fv and θ0 in Eq. (36).
” (i, k=r, θ, z) denote, respectively, the displacement and stress Green’s function, with the superscript “*” denoting the direction of the point-load upon appropriate specifications of Fh, Fv and θ0 in Eq. (36).
The solutions for displacement and stress Green’s functions due to a circular patch load of radius a with resultant Fh and Fv in horizontal and vertical directions, respectively, can also be expressed by Eqs. (40) and (41). In this case, the following relations for loading coefficient Xm, Ym and Zm in the source terms Eqs. (32) and (33) should be used:
 (42)
(42)
5 Special cases
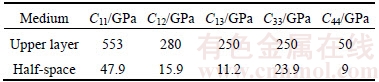
In this section, it is relevant to examine four degenerate cases: 1) when the exponential variation of the material properties for both of layers is zero, i.e., βI=βII=0, 2) when the exponential variation of the material properties for lower layer (z>h) is zero, i.e., βI=0, 3) when the elastic constants of the two layers 5.1 Homogeneous transversely isotropic two- layered half-space Upon setting βI=βII=0, the corresponding solution leads exactly to the one in KHOJASTEH et al [19], for the homogeneous transversely isotropic Two-layered half space in the static condition. 5.2 Homogeneous transversely half-space overlaid by an exponentially graded transversely isotropic coating layer Upon setting βII=0, the general solution leads to a homogeneous substrate with a FGM coating problem that solved for the first time in terms of transversely isotropic solids in this paper. Note that this special case is widely used for FGM coating- substrate systems in the engineering literature. 5.3 Exponentially graded transversely isotropic half- space Taking 5.4 Exponentially graded transversely isotropic bi-material Upon setting h→∞, the general solution leads to an exponentially graded transversely isotropic bi-material problem that solved for the first time in terms of transversely isotropic solids in this paper. 6 Numerical evaluation In the previous section, the point-load Green’s functions were expressed in terms of one- dimensional semi-infinite integrals. As the integrations generally cannot be carried out in exact closed-forms [24, 26, 30–32], a numerical quadrature technique usually has to be adopted in such evaluation. In order to evaluate the integrals accurately, it is very important to pay attention to the oscillatory nature of the integrands because of the presence of Bessel functions. In the present work, an adaptive quadrature rule demonstrated in RAHIMIAN et al [26] has been incorporated and used successfully. Several numerical examples are carried out to compare the present solution with the existing numerical solutions, with satisfactory results. A comparison has been carried out for the degenerate case of vertical displacements due to the vertical point-load at the (z=h) for an exponentially graded half-space with the results given in ESKANDARI and SHODJA [2], whose material properties are C11=41.3, C12=14.7, C13=10.1, C33= 36.2, C44=10.0. The evaluation was plotted in Figure 3, where a perfect agreement has been attained. Another comparison has been carried out for a surface load on an incompressible exponentially graded isotropic soil, with the initial shear modulus μ0=3.33, with result obtained by SELVADURAI and KATEBI [33]. The material constants for an isotropic medium can be reduced to C11=C33=λ+2μ, C12=C13=λ, C44=C66=μ, where λ and μ are the Lame’s constants of the isotropic solid. The results are shown in Figures 4 and 5, where an excellent agreement is observed between two results. For the third case, the thickness of upper layer h is equal to 1.5a. The value of engineering elastic constants for transversely isotropic materials are given in Table 1 [34], where Eh and Ev are the elastic moduli with respect to directions lying in the plane of isotropy and perpendicular to it; vh and vhv are Poisson ratios which characterize the effect of the horizontal strain on its orthogonal counterpart and the vertical strain (i.e., the z-direction strain), respectively; vvh is the Poisson ratio which characterizes the effect of the vertical strain on horizontal strains; and f/2 is the shear modulus for the planes normal to the plane of isotropy. Upon converting to the elasticity moduli Cij and choosing Figure 3 Displacement Green’s function Figure 4 Displacement Green’s function uz along z-axis obtained in this study compared with result reported by SELVADORAI and KATEBI [33] for static case due to uniform vertical surface load Figure 5 Displacement Green’s function uz at surface along r-axis obtained in this study compared with result reported by SELVADORAI and KATEBI [33] for static case due to uniform vertical surface load Table 1 Engineering constants of transversely isotropic materials Table 2 Elastic constants of transversely isotropic materials To illustrate the results obtained in previous sections, some typical point-load and circular patch-load Green’s functions are presented in Figures 9–25 for an exponentially graded transversely isotropic two-layered half-space. The values of the engineering elastic constants for considered transversely isotropic materials are given in Table 1. Figure 6 Comparison of stress Green’s function Table 3 Material constants of PAN problem Figure 7 Comparison of displacement Green’s function The four cases considered here are: Case 1: Exponentially graded two-layered with material 1 together βI in medium Ⅰ and material 2 together βII in medium Ⅱ. Figure 8 Comparison of stress Green’s function Figure 9 Displacement Green’s function Figure 10 Displacement Green’s function Case 2: Exponentially graded coating- substrate with material 1 together βI in medium Ⅰ and material 2 together βII=0 in medium Ⅱ. Figure 11 Displacement Green’s function Figure 12 Displacement Green’s function Figure 13 Displacement Green’s function Fig. 14 Stress Green’s function Figure 15 Stress Green’s function Figure 16 Displacement Green’s function Case 3: Exponentially graded half-space with material 2 in both media Ⅰ and Ⅱ Figure 17 Displacement Green’s function Figure 18 Stress Green’s function Figure 19 Contour of displacement Green’s function Figure 20 Contour of displacement Green’s function Figure 21 Amplitude of Case 4: Exponentially graded bi-material with material 1 together βI in medium Ⅰ and material 2 together βII in medium Ⅱ (h→∞). The thickness of the upper layer in cases 1 and 2 is taken equal to h=a where a is the radius of the circular patch load. The load is applied at the interface (z0=h) or surface (z0=0). It needs to be pointed out that all numerical results presented here are dimensionless, with a nondimensional inhomogeneity factor as β. The effects of inhomogeneity for five different cases of β=0, 0.1, 0.25, 0.5 and 1 on the Green’s functions are addressed. The displacement Green’s function Figure 22 Amplitude of Figure 23 Amplitude of The displacement Green’s functions are singular at the loading plane z=z0 and tend to zero with increasing depth. It is also observed that the displacement Green’s functions in three cases and two loading types generally decrease with increasing inhomogeneity factor β. The distributions of the stress Green’s functions Figure 24 Amplitude of Figure 25 Amplitude of Furthermore to provide further insight into the problem, the distributions of The effect of the upper layer together with inhomogeneity of layers on the response of the system is also of particular interest. For this purpose, the displacement Green’s functions 7 Conclusions The three-dimensional static Green’s functions of an exponentially graded transversely isotropic two-layered half-space due to the point-load and patch-load are derived by means of integral transforms and the method of displacement potentials. They are expressed in the form of explicit line-integral representations which are essential for the efficient boundary element formulations of the related elastoestatic problems and use in developing better evaluation of composites and anisotropic media. It is shown that the present exponentially graded transversely isotropic two-layered Green’s functions can analytically and numerically be degenerated to special transversely isotropic cases such as the solution for an exponentially graded bi-material and an exponentially graded coating on the homogeneous half-space. Numerical examples are also presented to elucidate the influence of the degree of non-homogeneity of the materials. References [1] SBURLATI R. Elastic solutions in a functionally graded coating subjected to a concentrated force [J]. Journal of Mechanics of Materials and Structures, 2012, 7: 401–412. [2] ESKANDARI M, SHODJA H M. Green’s functions of an exponentially graded transversely isotropic half-space [J]. International Journal of Solids and Structures, 2010, 47: 1537–1545. [3] KIEBACK B, NEUBRAND A, RIEDEL H. Processing techniques for functionally graded materials [J]. Materials Science and Engineering A, 2003, 362: 81–105. [4] SOBCZAK J, DRENCHEV L. Metallic functionally graded materials: A specific class of advanced composites [J]. Journal of Materials Science and Technology, 2013, 29(4): 297–316. [5] CHO J, ODEN J. Functionally graded material: a parametric study on thermal stress characteristics using the Crank-Nicolson-Galerkin scheme [J]. Computer Methods in Applied Mechanics and Engineering, 2000, 188: 17–38. [6] HORI M, NEMAT-NASSER S. On two micromechanics theories for determining micromacro relations in heterogeneous solids [J]. Mechanics of Materials, 1999, 31: 667–682. [7] RAHMAN S, CHAKRABORTY A. A stochastic micromechanical model for elastic properties of functionally graded materials [J]. Mechanics of Materials, 2007, 39: 548–563. [8] BIRMAN V, BYRD L W. Modeling and analysis of functionally graded materials and structures [J]. Applied Mechanics Reviews, ASME, 2007, 60(5): 195–216. [9] MARTIN P A, RICHARDSON J D, GRAY L J, BERGER J R. On Green’s function for a three-dimensional exponentially graded elastic solid [J]. Proceeding of the Royal Society of London, Series A, 2002, 458: 1931–1947. [10] WANG C D, PAN E, TZENG C S, HAN F, LIAO J J. Displacements and stresses due to a uniform vertical circular load in an inhomogeneous cross-anisotropic half-space [J]. International Journal of Geomechanic, 2006, 6(1): 110. [11] CHAN Y S, GREY L J, KAPLAN T, PAULINO G H. Green’s function for a two-dimensional exponentially graded elastic medium [J]. Proceefings of the Royal Society of London, Series A, 2004, 460: 1689–1706. [12] KASHTALYAN M, RUSHCHITSKY J J. Revisiting displacement functions in threedimensional elasticity of inhomogeneous media [J]. International Journal of Solids and Structures, 2009, 46: 3463–3470. [13] SALLAH O M, GRAY L J, AMER M A, MATBULY M S. Green’s function expantion for exponentially graded elasticity [J]. International Journal for Numerical Method in Engineering, 2010, 82: 756–772. [14] ESKANDARI-GHADI M, AMIRI-HEZAVEH A. Wave propagations in exponentially graded transversely isotropic half-space with potential function method [J]. Mechanics of Materials, 2014, 68: 275–292. [15] KATEBI A, SELVADURAI A P S. Undrained behaviour of a non-homogeneous elastic medium: the influence of variations in the elastic shear modulus with depth [J]. Geotechnique, 2013, 63(13): 1159–1169. [16] NING X, LOVELL M, SLAUGHTER W S. Asymptotic solutions for axisymmetric contact of thin, transversely isotropic elastic layer [J]. Wear, 2006, 260: 693–698. [17] RAHMAN M, NEWAZ G. Boussinesq type solution for a transversely isotropic half-space coated with a thin film [J]. International Journal of Engineering Science, 2000, 38: 807–822. [18] SHODJA H M, ESKANDARI M. Axisymmetric time-harmonic response of a transversely isotropic substrate–coating system [J]. International Journal of Engineering Science, 2007, 45: 272–287. [19] KHOJASTEH A, RAHIMIAN M, PAK R Y S, ESKADARI M. Asymmetric dynamic Green’s functions in a two-layered transversely isotropic half-space [J]. International Journal of Engineering science, ASCE, 2008, 134(9): 777–787. [20] KHOJASTEH A, RAHIMIAN M, PAK R Y S. Three-dimensional dynamic Green’s functions in transversely isotropic bi-materials [J]. International Journal of Solids and Structures, 2008, 45: 4952–4972. [21] KHOJASTEH A, RAHIMIAN M, ESKANDARI M. Three- dimensional dynamic Green’s functions in transversely isotropic tri-materials [J]. Applied Mathematical Modelling, 2013, 37: 3164–3180. [22] PAN E, YANG B. Three-dimensional interfacial Green’s functions in anisotropic bimaterials [J]. Applied Mathematical Modeling, 2003, 27: 307–326. [23] ESKANDARI-GHADI M, PAK R Y S, ARDESHIR- BEHRESTAGHI A. Transversely isotropic elastodynamic solution of a finite layer on an infinite subgrade under surface loads [J]. Soil Dynamics and Earthquake Engineering, 2008, 28: 986–1003. [24] KHOJASTEH A, RAHIMIAN M, ESKANDARI M, PAK R Y S. Three-dimensional dynamic Green’s functions for a multilayered transversely isotropic half-space [J]. International Journal of Solids and Structures, 2011, 48: 1349–1361. [25] ESKANDARI M, AHMADI S F. Green’s function of a surface-stiffened transversely isotropic half-space [J]. International Journal of Solids and Structures, 2012, 49: 3282–3290. [26] RAHIMIAN M, ESKANDARI-GHADI M, PAK R Y S, KHOJASTEH A. Elastodynamic potential method for transversely isotropic solid [J]. Journal of Engineering Mechanics, ASCE, 2007, 133(10): 1134–1145. [27] LEKHNITSKII S G. Theory of elasticity of an anisotropic elastic body [M]. San Francisco: Holden Day, 1963. [28] SNEDDON I N. Fourier transforms [M]. New York: Mcgraw-Hill, 1951. [29] SNEDDON I N. The use of integral transforms [M]. New York: Mcgraw-Hill, 1972. [30] APSEL R J, LUCO J E. On the Green’s functions for a layered half space [J]. Part II. Bulletin of the Seismological Society of America, 1983, 73(4): 931–951. [31] PAK R Y S, GUZINA B B. Three-dimensional Green’s functions for a multi-layered half-space displacement potentials [J]. Journal of Engineering Mechanics, ASCE, 2002, 128(4): 449–461. [32] RAJAPAKSE R K N D, WANG Y. Green’s functions for transversely isotropic elastic half-space [J]. Journal of Engineering Mechanics, ASCE, 1993, 119(9): 1724–1746. [33] SELVADURAI A P S, KATEBI A. Mindlin’s problem for an incompressible elastic half-space with an exponential variation in the linear elastic shear modulus [J]. International Journal of Engineering Science, 2013, 65: 9–21. [34] POULOS H G, DAVIS E H. Elastic solutions for soil and rock mechanics [M]. New York: Wiley, 1974. [35] PAN E. Static response of a transversely isotropic and layered half-space to general surface loads [J]. Physics of the Earth and Planetary Interiors, 1989, 54: 353–363. (Edited by HE Yun-bin) 中文导读 非对称格林函数的指数梯度横向各向同性基体涂层系统 摘要:通过研究一组完整的两个位移势,推导了指数梯度横向各向同性基体涂层系统弹性静力学格林函数的解析式。以线积分的形式表示三维点荷载和片荷载格林函数的应力和位移。该公式基于傅里叶级数和汉克尔变换,包括一组完整的转换应力-位移和位移-位势关系。为了便于说明,格林函数被简化为特殊情况,如指数级半空间和均匀双层半空间格林函数。由于被积函数的复杂性,对积分进行了数值计算,并且针对积分的数值计算,提出了一个强有力有效的方法,该方法考虑了积分奇点存在的情况。对现有的均匀双层各向同性和各向同性的半空间数值解进行比较,以确定本方案的准确性。通过典型的数值分析的例子,展示了指数梯度双层半空间格林函数的一般特征,据此可以识别材料性能变化程度。 关键词:功能梯度材料; 横向各向同性; 双材料; 格林函数; 涂层-基体; 位移势 Received date: 2016-08-29; Accepted date: 2017-12-01 Corresponding author: A. Khojasteh, PhD, Assistant Professor; Tel: +98–2161112174; E-mail: akhojasteh@ut.ac.ir; ORCID: 0000- 0002-6369-536x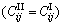 are equal, and 4) when the thickness of the upper layer (0<>
are equal, and 4) when the thickness of the upper layer (0<>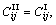 the corresponding solution leads exactly to the one in ESKANDARI and SHODJA [2], for the exponentially graded half- space problem with buried point and patch-loads.
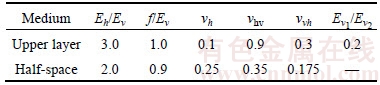
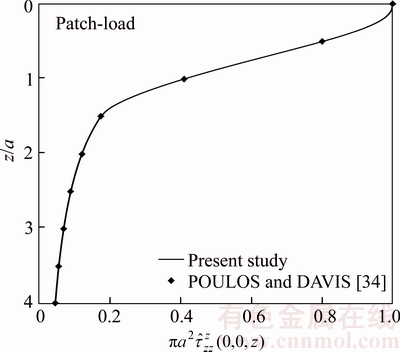
the corresponding solution leads exactly to the one in ESKANDARI and SHODJA [2], for the exponentially graded half- space problem with buried point and patch-loads. GPa, the pertinent elastic constants Cij can be stated as those given in Table 2. The normalized stress Green’s functions
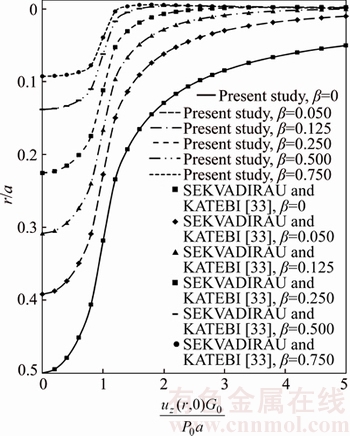
GPa, the pertinent elastic constants Cij can be stated as those given in Table 2. The normalized stress Green’s functions 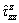 are compared as a function of depth z/a. The present results are compared with those reported by POULOS and DAVIS [34] in Figure 6 which are in an excellent agreement. To provide another comparison of the result for the homogeneous case, the thickness of upper layer h is equal to 2a. The value of the pertinent elastic constants Cij for this case is given in Table 3. The normalized displacement
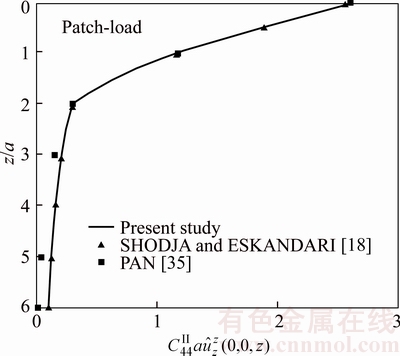
are compared as a function of depth z/a. The present results are compared with those reported by POULOS and DAVIS [34] in Figure 6 which are in an excellent agreement. To provide another comparison of the result for the homogeneous case, the thickness of upper layer h is equal to 2a. The value of the pertinent elastic constants Cij for this case is given in Table 3. The normalized displacement  and the stress component
and the stress component 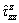 are computed as a function of depth z/a. The results are compared with those obtained by PAN [35] and SHODJA and ESKANDARI [18] in Figures 7 and 8, which are in a good agreement.
are computed as a function of depth z/a. The results are compared with those obtained by PAN [35] and SHODJA and ESKANDARI [18] in Figures 7 and 8, which are in a good agreement.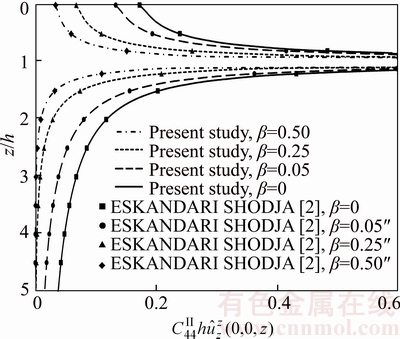
 along z-axis obtained in this study compared with result reported by ESKANDARI and SHODJA [2] under buried load
along z-axis obtained in this study compared with result reported by ESKANDARI and SHODJA [2] under buried load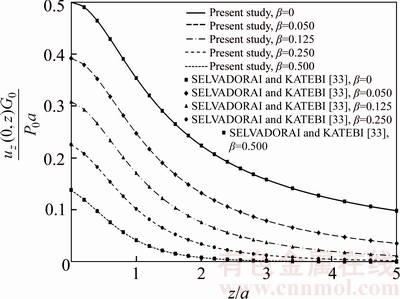
 of homogeneous transversely isotropic two-layered subjected to a surface patch-load of radius a and unit resultant
of homogeneous transversely isotropic two-layered subjected to a surface patch-load of radius a and unit resultant
 of homogeneous transversely isotropic multilayered half-space subjected to a surface patch-load of radius a and unit resultant
of homogeneous transversely isotropic multilayered half-space subjected to a surface patch-load of radius a and unit resultant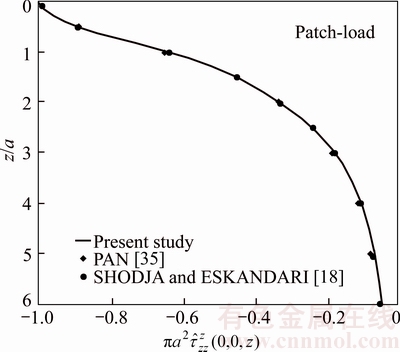
 of homogeneous transversely isotropic multilayered half- space subjected to a surface patch-load of radius a and unit resultant
of homogeneous transversely isotropic multilayered half- space subjected to a surface patch-load of radius a and unit resultant
 along z-axis due to unit point-load applied at interface (Case 1)
along z-axis due to unit point-load applied at interface (Case 1)
 along z-axis due to unit point-load applied at interface (Case 1)
along z-axis due to unit point-load applied at interface (Case 1)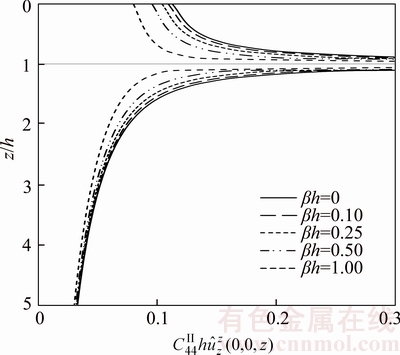
 along z-axis due to unit point-load applied at the interface (Case 2)
along z-axis due to unit point-load applied at the interface (Case 2)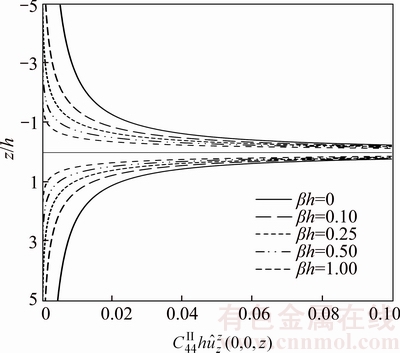
 along z-axis due to unit point-load applied at the interface (Case 4)
along z-axis due to unit point-load applied at the interface (Case 4)
 along z-axis due to patch-load with unit resultant applied at the interface (Case 2)
along z-axis due to patch-load with unit resultant applied at the interface (Case 2)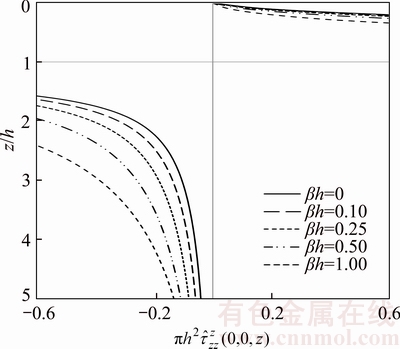
 along z-axis due to unit point-load applied at the interface (Case 1)
along z-axis due to unit point-load applied at the interface (Case 1)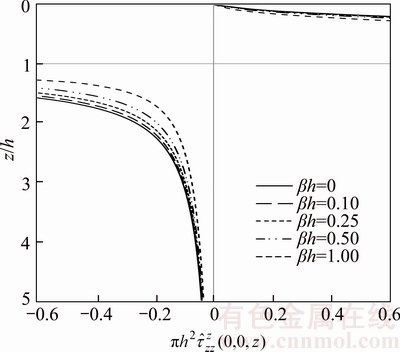
 along z-axis due to unit point-load applied at the interface (Case 2)
along z-axis due to unit point-load applied at the interface (Case 2)
 at interface along r-axis due to patch-load with radius a=h with unit resultant applied at interface (Case 2)
at interface along r-axis due to patch-load with radius a=h with unit resultant applied at interface (Case 2)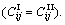
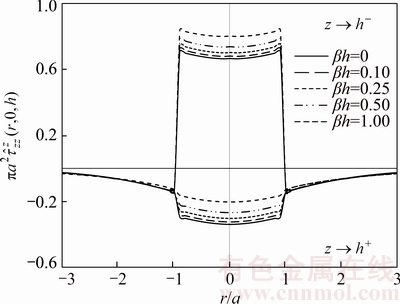
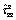 at interface along r-axis due to patch-load with radius a=h with unit resultant applied at interface (Case 2)
at interface along r-axis due to patch-load with radius a=h with unit resultant applied at interface (Case 2)
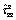 at the interface as a function of thickness h due to patch-load with unit resultant applied at interface (Case 2)
at the interface as a function of thickness h due to patch-load with unit resultant applied at interface (Case 2)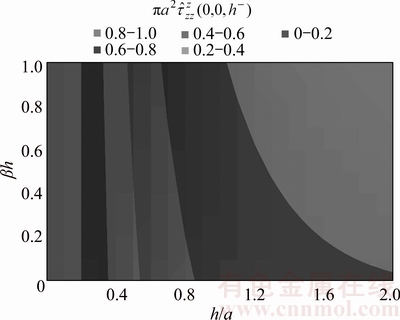
 as a function of thickness h and degree of inhomogeneity β due to patch-load with unit resultant applied at interface (Case 2)
as a function of thickness h and degree of inhomogeneity β due to patch-load with unit resultant applied at interface (Case 2)
 as a function of thickness h and degree of inhomogeneity β due to patch-load with unit resultant applied at interface (Case 2)
as a function of thickness h and degree of inhomogeneity β due to patch-load with unit resultant applied at interface (Case 2)
 along z-axis for Case 1, Case 2, and Case 3 due to unit point-load applied at interface
along z-axis for Case 1, Case 2, and Case 3 due to unit point-load applied at interface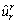 for case 1 due to the unit point-load in the r-direction at the interface are delineated in Fig. 9. Figures 10–12 depict the displacement Green’s functions
for case 1 due to the unit point-load in the r-direction at the interface are delineated in Fig. 9. Figures 10–12 depict the displacement Green’s functions 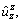 for three cases, due to the unit point-load in the z-direction at the interface. The displacement Green’s function
for three cases, due to the unit point-load in the z-direction at the interface. The displacement Green’s function 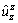 for case 2 due to the unit patch-load in the z-direction at the interface is delineated in Figure 13.
for case 2 due to the unit patch-load in the z-direction at the interface is delineated in Figure 13.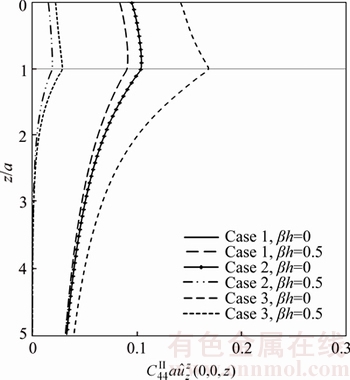
 along z-axis for Case 1, Case 2, and Case 3 due to unit patch-load applied at interface
along z-axis for Case 1, Case 2, and Case 3 due to unit patch-load applied at interface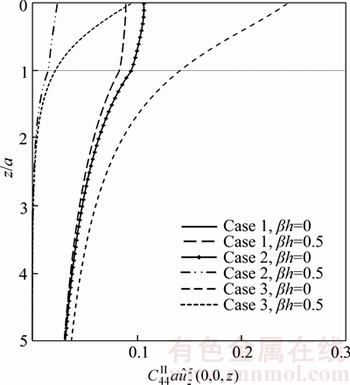
 along z-axis for Case 1, Case 2, and Case 3 due to unit patch-load applied at surface
along z-axis for Case 1, Case 2, and Case 3 due to unit patch-load applied at surface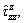 for cases 1 and 2, due to the unit point-load in the z-direction at the interface are plotted in Figures 14 and 15. Similar to the displacement Green’s functions, the stress Green’s functions are singular at the loading plane z=z0 and tend to zero with increasing depth. As inhomogeneity factor β increases, the stress Green’s functions increase in some parts graded. The reason of this increase is existence the factor eβz in stress Green’s functions.
for cases 1 and 2, due to the unit point-load in the z-direction at the interface are plotted in Figures 14 and 15. Similar to the displacement Green’s functions, the stress Green’s functions are singular at the loading plane z=z0 and tend to zero with increasing depth. As inhomogeneity factor β increases, the stress Green’s functions increase in some parts graded. The reason of this increase is existence the factor eβz in stress Green’s functions.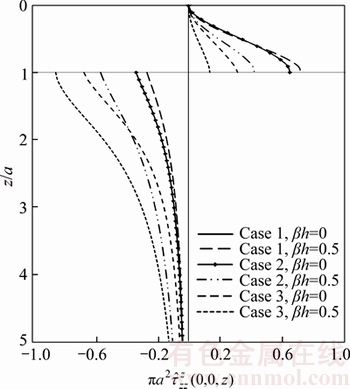
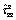 along z-axis for Case 1, Case 2, and Case 3 due to unit patch-load applied at interface
along z-axis for Case 1, Case 2, and Case 3 due to unit patch-load applied at interface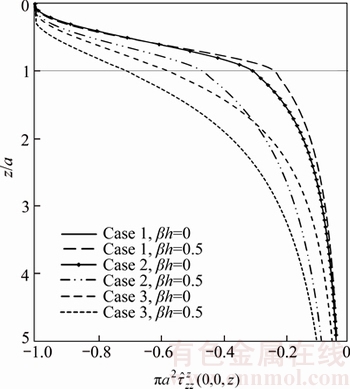
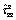 along z-axis for Case 1, Case 2, and Case 3 due to unit patch-load applied at surface
along z-axis for Case 1, Case 2, and Case 3 due to unit patch-load applied at surface and
and 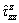 for case 2, due to the patch-load applied at the z0=h, along the r-axis are shown in Figures 16 and 17, respectively. Figrue 18 depicts stress Green’s functions
for case 2, due to the patch-load applied at the z0=h, along the r-axis are shown in Figures 16 and 17, respectively. Figrue 18 depicts stress Green’s functions 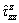 for case 2 due to the patch-load with unit resultant in the z-direction applied at the interface, as a function of dimensionless thickness h for different β. Figures 19 and 20 display contours of nondimensional displacement and stress Green’s functions due to the patch-load applied at the interface, and show evidently the effects of both thickness h and inhomogeneity β.
for case 2 due to the patch-load with unit resultant in the z-direction applied at the interface, as a function of dimensionless thickness h for different β. Figures 19 and 20 display contours of nondimensional displacement and stress Green’s functions due to the patch-load applied at the interface, and show evidently the effects of both thickness h and inhomogeneity β. and stress Green’s functions
and stress Green’s functions 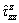 pertinent to cases 1, 2, and the FGM half-space with medium II properties are also examined. The unit point-load and patch-load applied at z=z0 with inhomogeneity factor β=0, 0.5 are considered. Figures 21–25 depict these results. From Figures 21–23, it is evident that insertion of a hard upper layer results in a substantial decrease in
pertinent to cases 1, 2, and the FGM half-space with medium II properties are also examined. The unit point-load and patch-load applied at z=z0 with inhomogeneity factor β=0, 0.5 are considered. Figures 21–25 depict these results. From Figures 21–23, it is evident that insertion of a hard upper layer results in a substantial decrease in 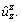
Abstract: By virtue of a complete set of two displacement potentials, an analytical derivation of the elastostatic Green’s functions of an exponentially graded transversely isotropic substrate–coating system is presented. Three-dimensional point–load and patch–load Green’s functions for stresses and displacements are given in line-integral representations. The formulation includes a complete set of transformed stress–potential and displacement–potential relations, with utilizing Fourier series and Hankel transforms. As illustrations, the present Green’s functions are degenerated to the special cases such as an exponentially graded half-space and a homogeneous two-layered half-space Green’s functions. Because of complicated integrand functions, the integrals are evaluated numerically and for numerical computation of the integrals, a robust and effective methodology is laid out which gives the necessary account of the presence of singularities of integration. Comparisons of the existing numerical solutions for homogeneous two-layered isotropic and transversely isotropic half-spaces are made to confirm the accuracy of the present solutions. Some typical numerical examples are also given to show the general features of the exponentially graded two-layered half-space Green’s functions that the effect of degree of variation of material properties will be recognized.


