Trans. Nonferrous Met. Soc. China 29(2019) 775-784
Prediction of grain scale plasticity of NiTi shape memory alloy based on crystal plasticity finite element method
Li HU1, Shu-yong JIANG 2, Lai-xin SHI1, Yan-qiu ZHANG2
1. College of Material Science and Engineering, Chongqing University of Technology, Chongqing 400054, China;
2. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China
Received 27 May 2018; accepted 9 July 2018
Abstract:
Grain scale plasticity of NiTi shape memory alloy (SMA) during uniaxial compression deformation at 400 °C was investigated through two-dimensional crystal plasticity finite element simulation and corresponding analysis based on the obtained orientation data. Stress and strain distributions of the deformed NiTi SMA samples confirm that there exhibits a heterogeneous plastic deformation at grain scale. Statistically stored dislocation (SSD) density and geometrically necessary dislocation (GND) density were further used in order to illuminate the microstructure evolution during uniaxial compression. SSD is responsible for sustaining plastic deformation and it increases along with the increase of plastic strain. GND plays an important role in accommodating compatible deformation between individual grains and thus it is correlated with the misorientation between neighboring grains, namely, a high GND density corresponds to large misorientation between grains and a low GND density corresponds to small misorientation between grains.
Key words:
grain scale plasticity; NiTi shape memory alloy; crystal plasticity finite element method; plastic deformation; microstructure evolution;
1 Introduction
By virtue of a reversible martensite phase transformation between a high-symmetry austenite B2 phase and a low-symmetry martensite B19′ phase, NiTi-based shape memory alloys (SMAs) are exploited for a plenty of applications in different fields including materials science and engineering [1,2]. As a widely used kind of NiTi-based SMAs, binary NiTi SMAs have attracted much attention in fundamental material studies due to their excellent superelasticity, outstanding shape memory effect and perfect biological compatibility [3,4]. Plastic deformation plays a dominant role in manufacturing workpieces of NiTi SMA products. It is worth mentioning that plastic deformation has a strong impact on the microstructure evolution of NiTi SMAs, and therefore further affects the mechanical properties and shape memory effect [5,6]. So far, investigations have been conducted mainly in the fields of superelastic deformation and transformation-induced plasticity of NiTi SMAs [7-10]. Notwithstanding small plastic deformation involved in these studies, previous researches contributed to clarifying the nature and significance of various deformation mechanisms, and further clearly discerned the plastic deformation occurred in NiTi SMAs under different deformation conditions. However, literatures are still scarce in terms of mechanical response and microstructure evolution of NiTi SMAs subjected to large plastic deformation.
It is generally accepted that experimental methods suffer from a few drawbacks about revealing plastic deformation mechanisms and microstructure evolution of metallic alloys during plastic deformation, so numerical simulation technique, particularly the crystal plasticity finite element method (CPFEM), has become an efficient and versatile simulation tool for clarifying plastic deformation mechanisms and microstructure evolution of metallic alloys [11,12]. CPFEM refers to the particular mechanical regime addressed by means of the crystal plasticity (CP) theory as well as the approach on the basis of finite element method (FEM). As to crystal plasticity theory, the pioneering work was made by TAYLOR [13], and this theory is on the basis of rather simple boundary condition that the grains suffer from homogeneous deformation. Then, based on Taylor model, HILL and RICE [14], and ASARO and RICE [15] successfully described the geometry and kinematics of crystal plastic deformation. Afterwards, a rigorous constitutive framework established by PEIRCE et al [16], and ASARO and NEEDLEMAN [17] was put forward to simulate material response and texture evolution in finite deformation. Thereafter, the crystal plasticity theory is incorporated into finite element method, forming the CPFEM, which can meet the requirements for the equilibrium of the forces and the compatibility of the displacements using a weak form of the principle of virtual work in a given finite-volume element [18]. More recent researches have been conducted in consideration of various deformation modes, including dislocation slip [19,20], martensite transformation [21,22] as well as deformation twinning [23,24] in order to capture the global mechanical response, the intra-granular and inter-granular heterogeneities in polycrystal as well as texture evolution during plastic deformation [25,26]. In conclusion, CPFEM contributes to better understanding plastic deformation of metallic alloys at grain scale.
In the present study, crystal plasticity finite element (CPFE) simulation and corresponding analysis on the basis of the meshed orientation data obtained from simulation results were performed in order to investigate microstructure evolution and inhomogeneous plastic deformation throughout uniaxial compression of NiTi SMA at 400 °C.
2 Crystal plasticity model
2.1 Constitutive model
It has been confirmed that there is not deformation twinning in the Ni50.9Ti49.1 (at.%) SMA sample suffered from uniaxial compression at 400 °C [27]. Moreover, martensite desist temperature Md is lower than 400 °C. Consequently, martensite phase transformation does not occur at 400 °C and there are totally 24 individual slip systems to contribute to satisfying requirements for generalized plasticity, including {110}<100>, {010}<100> and {110}<111> slip modes [3].
The constitutive behavior of NiTi SMA was illuminated by crystal plasticity theory to capture the slip-based plastic deformation of polycrystal. Therefore, the code initially developed by HUANG [28] was used in the present study in order to capture the material flow via dislocation motion. The detailed content with respect to equations of crystal plasticity theory and numerical implementation as user-supplied subroutine UMAT in the finite element code ABAQUS are not specified here. However, to be self-consistent, only the key equations are reported.
The total deformation gradient F can be multiplicatively decomposed into the elastic component and plastic component [14,15].
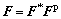(1)
where F* represents the elastic deformation gradient incorporating the elastic stretch and rigid body rotation of a crystal lattice, and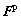 
stands for the plastic deformation gradient and it delegates the dislocation slip in slip planes.
The velocity gradient L can also be decomposed into two components as follows:
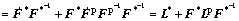(2)
where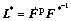 
represents an elastic part and 
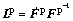stands for a plastic part. Moreover, 
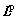reflects the slipping rate 
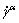of α slip system and it can be calculated by the following equation:
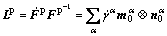(3)
where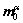 
is the unit vector standing for the slip direction, 
is the unit vector representing the normal to the slip plane in the intermediate configuration,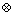 
denotes the dyadic product of two vectors. Moreover, vectors 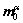and in the intermediate configuration correlate with the corresponding vectors 
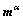and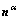 
in the current configuration by the following equation:
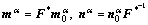(4)
The slipping shear rate 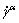on α slip system can be calculated by a power law relation proposed by PEIRCE et al [16] via the resolved shear stress 
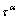and the slip resistance gα:
(5)
where n denotes the rate dependency. ABDOLVAND et al [23] have reported that if the material is rate-independent, a large value of n can be chosen up to 50, whereas if the material is highly rate-dependent, a typical value of 10 can be used. In the present study, the value of n is chosen to be 20, indicating a certain rate dependency of the adopted NiTi SMA [4]. 
is a reference shear strain rate and its value is chosen to be 0.001 s-1 and it is consistent with the macroscopic strain rate.
During the plastic deformation, the evolution of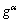 
through a phenomenological model proposed by PEIRCE et al [16] is shown as follows:
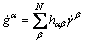(6)
where N stands for the number of all slip systems used in crystal plasticity finite element simulation and its value is 24. hαβ is the slip hardening modulus including self-hardening modulus hαβ (α=β) and latent-hardening modulus hαβ (α≠β). Furthermore, the hardening model is given by the following equation:
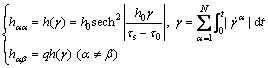(7)
where h0 is the initial hardening modulus, τ0 is the initial yield stress and its value equals the initial value of the strength gα, τs denotes the saturation stress, γ is the cumulative shear strain on all slip systems, q is the ratio of latent hardening to self hardening and q=1.4 is adopted in the present study.
2.2 Finite element model based on Voronoi tessellation
Emphases of the present study were focused on understanding the inhomogeneous plastic deformation and microstructure evolution at grain scale. Therefore, representative volume element (RVE) model with refined mesh by means of Voronoi tessellation was used in the present study and was constructed via a free open source software package NEPER [29]. In addition, the constructed model is based on the electron backscattered diffraction (EBSD) experiments conducted on two cross-sections of the initial specimen, i.e. the rolling direction and normal direction (RD-ND) and transverse direction and normal direction (TD-ND) sections, as shown in Fig. 1. The scan step was chosen to be 2 μm in synthetical consideration of scanning resolution and scanning time. It is obvious in Fig. 1 that the initial microstructure consists of equiaxed grains and the equivalent grain diameter is finally determined to be about 25 μm. Moreover, in the constructed RVE model, each grain is grouped into element sets and assigned to a specific crystallographic orientation by means of discretizing the orientation distribution function (ODF) of EBSD data. Specific details about orientation discretization and orientation assignment can be found in Ref. [30]. In addition, the boundary condition applied in the adopted RVE model is the simplified periodic boundary condition as specified in Ref. [31] and the RVE model would be compressed in y direction at the strain rate of 0.001 s-1. It is worth mentioning that this kind of boundary condition can be established easily. Moreover, it has been verified that there is no great difference in the result of material response anyway [31,32].
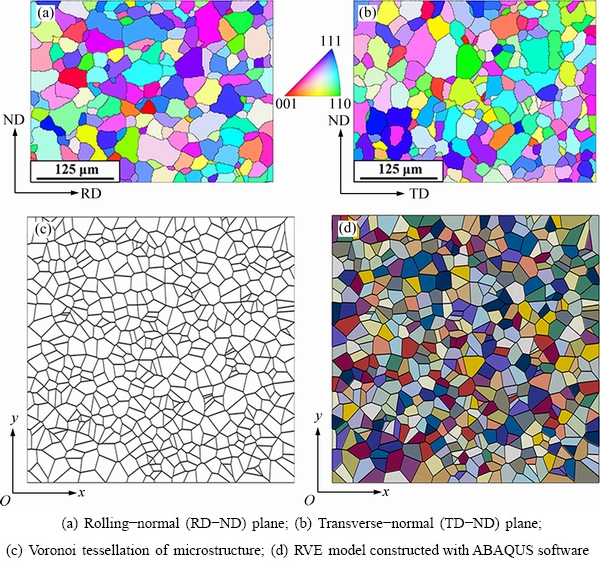
Fig. 1 RVE model for NiTi SMA on basis of Voronoi tessellation and statistical analysis of individual grains in two EBSD scan areas
2.3 Parameters calibration
Anisotropic values of elastic parameters, C11, C12 and C44, for NiTi SMA are determined as C11=130 GPa, C12=98 GPa and C44=34 GPa [9]. Using these elastic constants, finite element analysis of the RVE model subjected to uniaxial compression gives a global elastic modulus of 77 GPa for NiTi SMA at 400 °C, which matches the experimental measurement.
A validation of the constructed RVE model is given according to the following two aspects: (1) whether it reflects the characteristic of individual grains in NiTi SMA, and (2) whether the model consists of enough grains and finite elements. Figure 2(a) shows the statistical analysis of equivalent grain diameter in the constructed microstructure. It can be found that the equivalent grain diameter is about 25 μm, and it is similar to the corresponding value obtained by virtue of the statistical analysis of individual grains in each scanning area in Fig. 1. Moreover, Figs. 2(b) and (c) show the convergence analysis of the grain number and finite elements, and it can be confirmed that the constructed RVE model, which contains 512 grains and 130915 plane strain elements, finally meets the requirement for simulation convergence. After the validation of adopted RVE model, a “trial-error” procedure is used to optimize the numerical result, which is compared with the mechanical response in experiment. The specific details about uniaxial compression experiment of NiTi SMA samples at 400 °C are not specified here and these contents can be found in Ref. [33]. Finally, in this way, a good accordance is achieved between the predicted stress-strain curve and the experimental stress-strain curve, as shown in Fig. 2(d), and thus a set of adopted material parameters are shown in Table 1.
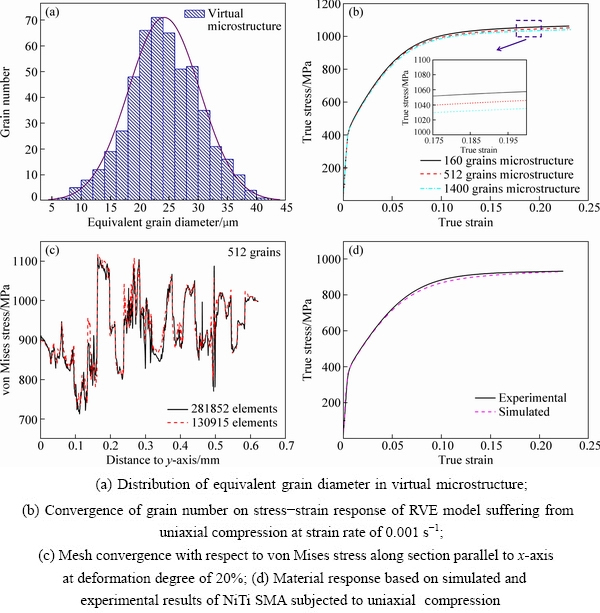
Fig. 2 Validity of constructed RVE model and material response based on experiment and CPFEM
Table 1 Adopted material parameters of NiTi SMA
3 Results and discussion
3.1 Distributions of strain and stress during plastic deformation
Figure 3(a-d) depicts the evolution of maximum principal strain at different deformation degrees. It can be seen that the distribution of maximum principal strain is inhomogeneous at grain scale and the maximum value in the color bar tends to appear within the shear bands across multiple grains. The shear bands are of the most typical feature in the contour plots of maximum principal strain, and they are aligned with the compression axis by an angle of 45°. This observation is consistent with that obtained from the macroscopic uniaxial compression. Similarly, heterogeneous stress distribution can also be clearly observed in Figs. 3(e-h). The grains with harder and softer orientations reach correspondingly higher and lower level of stress, respectively. Furthermore, the stress concentrations with the highest values trend to emerge near the grain boundaries, and this aspect has been confirmed in Ref. [34].
3.2 Coupling crystal plasticity finite element model with EBSD measurement
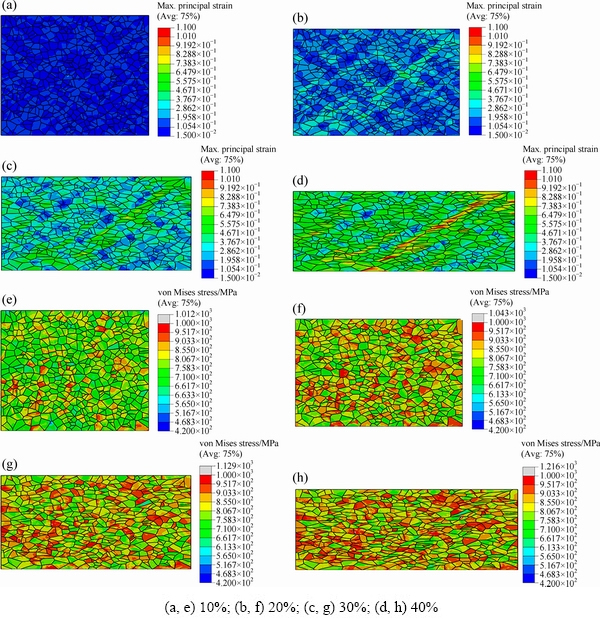
Fig. 3 Contour plots of maximum principal strain (a-d) and von Mises stress (e-h) of constructed RVE model under uniaxial compression at different deformation degrees
Based on the aforementioned results, the heterogeneous distributions of strain and stress during uniaxial compression of NiTi SMA can be predicted by means of CPFE simulation. State variables including maximum principal strain, von Mises stress, three Euler angles and so on, prove to be valuable in demonstrating information at a material point. A drawback of CPFE simulation is that some features with respect to microstructure evolution, are unable to be predicted during plastic deformation because the Euler angles are not able to be directly analyzed in crystal plasticity finite element simulation. It is generally accepted that EBSD measurement is a perfect candidate for capturing the evolution of microstructure in metallic alloys during plastic deformation. The format of data used in EBSD measurement is regular and equally spaced according to the scanning area and scanning step size. Therefore, if the data obtained from finite element simulation can be analyzed in a way which is used to handle EBSD data, a deep-insight investigation can be performed to characterize the microstructure features during plastic deformation. It is worth mentioning that these state variables involving in CPFE simulation are provided at the spatial positions of the integration points within the distorted finite elements. Thus, the format of data directly obtained from finite element model is not matched with the format of data used in EBSD analysis. Therefore, it is necessary to map the crystal orientations and other state variables from the irregular points in CPFE model onto the regular points in the mesh, which can be used to conduct EBSD analysis. The mapping procedure is realized by directly interpolating the finite element data linearly and the details of the adopted method can be found in Ref. [35]. Subsequently, a comparison is conducted between the distribution of the maximum principal strain obtained from CPFE simulation and the corresponding one by means of linear interpolation approach, as shown in Fig. 4. Obviously, the contour plot directly obtained from CPFE simulation is in accordance with the linearly interpolated one. This fact provides a favorable proof on the validity of adopted mapping approach.
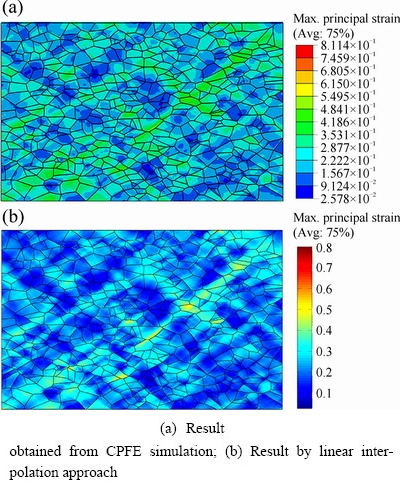
Fig. 4 Comparison between contour plots of maximum principal strain at deformation degree of 20%
3.3 Effect of statistically stored dislocation during plastic deformation
Using the method adopted in Ref. [35], statistically stored dislocation (SSD) density at each integration point can be calculated via the following equation:
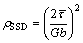(8)
where b denotes the magnitude of Burgers vector, G represents the shear modulus, and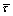 
stands for the average resolved shear stress with respect to all activated slip systems and it is calculated by the following equation:
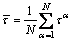(9)
Figure 5 shows the evolution of SSD density during plastic deformation. The simulated results denote that the distributions of SSD density at different deformation degrees are highly inhomogeneous. It can be noted that the high SSD density is not only concentrated near some grain boundaries, but also concentrated within some grain interiors. This observation can be enhanced by the fact that SSD is the dominant carrier to sustain plastic deformation and heterogeneous plastic deformation at grain scale is unavoidable due to different grain morphologies and grain orientations. Another interesting result in Fig. 5 is that the locations with large value of SSD density are similar to those with large plastic strain within the shear bands in Fig. 3. Consequently, it can be deduced that on the one hand, some areas of individual grains suffer from large plastic deformation, thus they possess large SSD density. On the other hand, some areas of individual grains sustain small plastic deformation, thus they have relatively small SSD density.
3.4 Effect of geometrically necessary dislocation during plastic deformation
It is generally accepted that the geometrically necessary dislocation (GND) plays an indispensable role in accommodating plastic deformation between individual grains. The GND density can be estimated from an EBSD measurement [36]. Since there are orientation differences θ of neighboring measurement pixels in scanning area, GND is required to compensate the orientation gradient in the crystal lattice. Its density is defined as υ, which can be estimated by the following equation.
(10)
where p stands for the size of a pixel. From the orientation differences between neighboring pixels, the dislocation tensor (Nye tensor) can be derived and its corresponding entry-wise norm gives a scalar GND density.
(11)
Figure 6 shows the maps of GND density measured from EBSD experiments, where the grain boundaries are superimposed. The corresponding calculation is also performed through the MATLAB toolbox MTEX. The maps of GND density indicate that with the progression of plastic deformation, GND density is dominant at grain boundaries and some areas inside individual grains also possess high GND density. The corresponding maps of GND density on the basis of the regular orientation data obtained by means of mapping approach are shown in Fig. 7. Features of the simulated GND density distribution are consistent with the experimental observations. Furthermore, it can be seen that the simulated GND density is about three orders of magnitude higher than the experimental one. This phenomenon is mainly attributed to the fact that the CPFE simulation has been performed under the condition of two-dimensional uniaxial compression. Therefore, the grain rotation has been limited within the two-dimension plane, which results in larger GND density to accommodate the compatible deformation among individual grains.
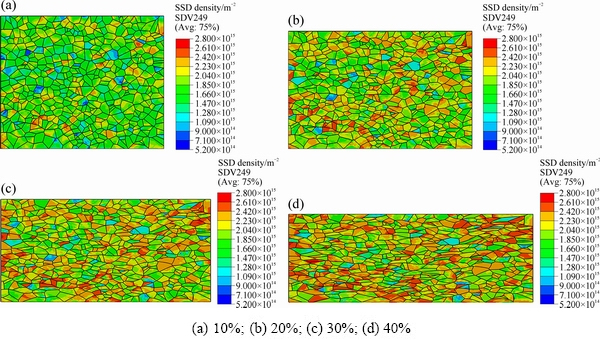
Fig. 5 Contour plots of SSD density of adopted RVE model under uniaxial compression at different deformation degrees
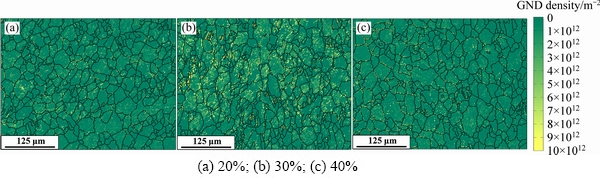
Fig. 6 Distributions of GND density in scanning areas within microstructures of NiTi SMA under uniaxial compression at different deformation degrees
Fig. 7 Distributions of GND density in adopted RVE model under uniaxial compression at different deformation degrees
Figure 8 shows the evolution of grain boundary misorientation between individual grains at different deformation degrees. By comparing Fig. 7 with Fig. 8, it can be obviously seen that the grain boundary corresponding to large grain boundary misorientation possesses relatively high GND density, whereas the grain boundary corresponding to small grain boundary misorientation possesses relatively low GND density. This observation is in good accordance with the results reported in Ref. [37].
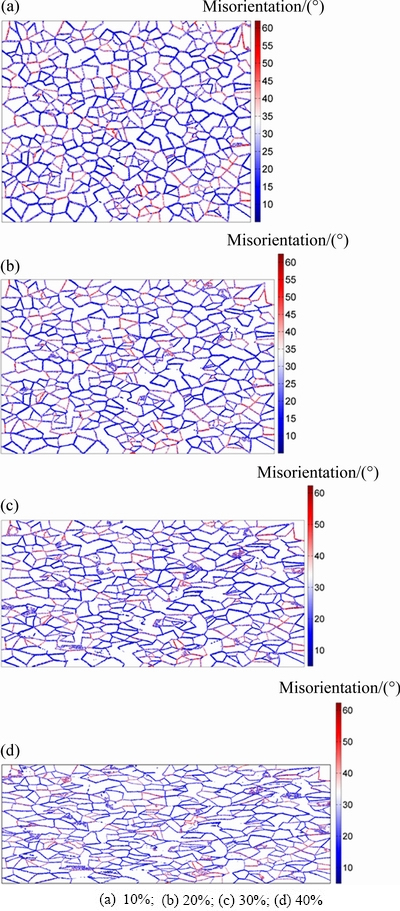
Fig. 8 Distributions of grain boundary misorientation between individual grains in adopted RVE model under uniaxial compression at different deformation degrees
4 Conclusions
(1) Inhomogeneous plastic deformation and microstructure evolution of NiTi SMA suffering from uniaxial compression deformation at 400 °C are investigated at grain scale via two-dimensional CPFE simulation.
(2) According to stress and strain distributions, it can be noted that NiTi SMA exhibits an inhomogeneous plastic deformation at grain scale. As a result of heterogeneous plastic deformation, the shear bands are aligned with the compression axis by an angle of 45°.
(3) The distribution of SSD density is inhomogeneous at grain scale during uniaxial compression. Moreover, SSD plays a significant role in sustaining plastic deformation, and consequently SSD density increases with increasing the plastic deformation degree.
(4) GND contributes to accommodating the compatible deformation between grains and thus the distribution of GND density is consistent with that of misorientation between grains. High GND density corresponds to large misorientation between grains and low GND density corresponds to small misorientation between grains.
References
[1] JANI J M, LEARY M, SUBIC A, GIBSON M A. A review of shape memory alloy research, applications and opportunities [J]. Materials & Design, 2014, 56: 1078-1113.
[2] JIANG P C, ZHENG Y F, TONG Y X, CHEN F, TIAN B, LI L, GUNDEROV D V, VALIEV R Z. Transformation hysteresis and shape memory effect of an ultrafine-grained TiNiNb shape memory alloy [J]. Intermetallics, 2014, 54: 133-135.
[3] BENAFAN O, NOEBE R, PADULA S, GARG A, CLAUSEN B, VOGEL S, VAIDYANATHAN R. Temperature dependent deformation of the B2 austenite phase of a NiTi shape memory alloy [J]. International Journal of Plasticity, 2013, 51: 103-121.
[4] JIANG S Y, ZHANG Y Q, ZHAO Y N, TANG M, YI W L. Constitutive behavior of Ni-Ti shape memory alloy under hot compression [J]. Journal of Central South University, 2013, 20(1): 24-29.
[5] MIRZADEH H, PARSA M H. Hot deformation and dynamic recrystallization of NiTi intermetallic compound [J]. Journal of Alloys and Compounds, 2014, 614: 56-59.
[6] BASU R, JAIN L, MAJI B, KRISHNAN M. Dynamic recrystallization in a Ni-Ti-Fe shape memory alloy: Effects on austenite–martensite phase transformation [J]. Journal of Alloys and Compounds, 2015, 639: 94-101.
[7] YU C, KANG G, KAN Q. A micromechanical constitutive model for anisotropic cyclic deformation of super-elastic NiTi shape memory alloy single crystals [J]. Journal of the Mechanics and Physics of Solids, 2015, 82: 97-136.
[8] YIN H, HE Y, SUN Q. Effect of deformation frequency on temperature and stress oscillations in cyclic phase transition of NiTi shape memory alloy [J]. Journal of the Mechanics and Physics of Solids, 2014, 67: 100-128.
[9] MANCHIRAJU S, ANDERSON P M. Coupling between martensitic phase transformations and plasticity: A microstructure-based finite element model [J]. International Journal of Plasticity, 2010, 26(10): 1508-1526.
[10] MAO S, LI H, LIU Y, DENG Q, WANG L, ZHANG Y, ZHANG Z, HAN X. Stress-induced martensitic transformation in nanometric NiTi shape memory alloy strips: An in situ TEM study of the thickness/size effect [J]. Journal of Alloys and Compounds, 2013, 579: 100-111.
[11] ARDELJAN M, BEYERLEIN I J, MCWILLIAMS B A, KNEZEVIC M. Strain rate and temperature sensitive multi-level crystal plasticity model for large plastic deformation behavior: Application to AZ31 magnesium alloy [J]. International Journal of Plasticity, 2016, 83: 90-109.
[12] LATYPOV M I, SHIN S, de COOMAN B C, KIM H S. Micromechanical finite element analysis of strain partitioning in multiphase medium manganese TWIP+TRIP steel [J]. Acta Materialia, 2016, 108: 219-228.
[13] TAYLOR G I. Plastic strain in metals [J]. Journal of Institute of Metals, 1938, 62: 307-324.
[14] HILL R, RICE J. Constitutive analysis of elastic-plastic crystals at arbitrary strain [J]. Journal of the Mechanics and Physics of Solids, 1972, 20(6): 401-413.
[15] ASARO R J, RICE J. Strain localization in ductile single crystals [J]. Journal of the Mechanics and Physics of Solids, 1977, 25(5): 309-338.
[16] PEIRCE D, ASARO R, NEEDLEMAN A. An analysis of nonuniform and localized deformation in ductile single crystals [J]. Acta Metallurgica, 1982, 30(6): 1087-1119.
[17] ASARO R J, NEEDLEMAN A. Overview No. 42 texture development and strain hardening in rate dependent polycrystals [J]. Acta Metallurgica, 1985, 33(6): 923-953.
[18] ROTERS F, EISENLOHR P, HANTCHERLI L, TJAHJANTO D D, BIELER T R, RAABE D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications [J]. Acta Materialia, 2010, 58(4): 1152-1211.
[19] ZHANG H M, DONG X H, WANG Q, LI H Z. Micro-bending of metallic crystalline foils by non-local dislocation density based crystal plasticity finite element model [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(11): 3362-3371.
[20] CHEN S D, LIU X H, LIU L Z. Grain statistics effect on deformation behavior in asymmetric rolling of pure copper foil by crystal plasticity finite element model [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(10): 3370-3380.
[21] KAN Q, KANG G. Constitutive model for uniaxial transformation ratchetting of super-elastic NiTi shape memory alloy at room temperature [J]. International Journal of Plasticity, 2010, 26(3): 441-465.
[22] LEE M G, KIM S J, HAN H N. Crystal plasticity finite element modeling of mechanically induced martensitic transformation (MIMT) in metastable austenite [J]. International Journal of Plasticity, 2010, 26(5): 688-710.
[23] ABDOLVAND H, DAYMOND M R, MAREAU C. Incorporation of twinning into a crystal plasticity finite element model: Evolution of lattice strains and texture in Zircaloy-2 [J]. International Journal of Plasticity, 2011, 27(11): 1721-1738.
[24] GAN Y, SONG W, NING J, TANG H, MAO X. An elastic–viscoplastic crystal plasticity modeling and strain hardening for plane strain deformation of pure magnesium [J]. Mechanics of Materials, 2016, 92: 185-197.
[25] SHEIKH H, EBRAHIMI R, BAGHERPOUR E. Crystal plasticity finite element modeling of crystallographic textures in simple shear extrusion (SSE) process [J]. Materials & Design, 2016, 109: 289-299.
[26] SHEIKH H, EBRAHIMI R. Investigation on texture evolution during cyclic expansion-extrusion (CEE) technique using crystal plasticity finite element modeling [J]. Journal of Materials Science, 2016, 51(22): 10178-10190.
[27] HU L, JIANG S Y, ZHANG Y Q, ZHAO Y N, LIU S W, ZHAO C Z. Multiple plastic deformation mechanisms of NiTi shape memory alloy based on local canning compression at various temperatures [J]. Intermetallics, 2016, 70: 45-52.
[28] HUANG Y G. A user-material subroutine incroporating single crystal plasticity in the ABAQUS finite element program [M]. Cambridge: Harvard University Press, 1991.
[29] QUEY R, DAWSON P, BARBE F. Large-scale 3D random polycrystals for the finite element method: Generation, meshing and remeshing [J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(17): 1729-1745.
[30] LI L T, LIN Y, LI L, SHEN L M, WEN D X. Three-dimensional crystal plasticity finite element simulation of hot compressive deformation behaviors of 7075 Al alloy [J]. Journal of Materials Engineering and Performance, 2015, 24(3): 1294-1304.
[31] LI Y, PAN X, WU G, WANG G. Shape-instability life scatter prediction of 40Cr steel: Damage-coupled crystal plastic probabilistic finite element method [J]. International Journal of Plasticity, 2016, 79: 1-18.
[32] ZHANG K S, JU J W, LI Z, BAI Y L, BROCKS W. Micromechanics based fatigue life prediction of a polycrystalline metal applying crystal plasticity [J]. Mechanics of Materials, 2015, 85: 16-37.
[33] HU L, JIANG S Y, ZHANG Y Q, SUN D. Crystal plasticity finite element simulation of NiTi shape memory alloy based on representative volume element [J]. Metals and Materials International, 2017, 23(6): 1075-1086.
[34] KHADYKO M, MARIOARA C D, RINGDALEN I G, DUMOULIN S, HOPPERSTAD O S. Deformation and strain localization in polycrystals with plastically heterogeneous grains [J]. International Journal of Plasticity, 2016, 86: 128-150.
[35] LAN Y, XIAO N, LI D, LI Y. Mesoscale simulation of deformed austenite decomposition into ferrite by coupling a cellular automaton method with a crystal plasticity finite element model [J]. Acta Materialia, 2005, 53(4): 991-1003.
[36] PANTLEON W. Resolving the geometrically necessary dislocation content by conventional electron backscattering diffraction [J]. Scripta Materialia, 2008, 58(11): 994-997.
[37] TOTH L S, GU C. Ultrafine-grain metals by severe plastic deformation [J]. Materials Characterization, 2014, 92: 1-14.
基于晶体塑性有限元法预测NiTi形状记忆合金的晶粒尺度塑性
胡 励1，江树勇2，时来鑫1，张艳秋2
1. 重庆理工大学 材料科学与工程学院，重庆 400054；
2. 哈尔滨工程大学 机电工程学院，哈尔滨 150001
摘 要：通过二维晶体塑性有限元模拟和相应取向数据分析，研究NiTi形状记忆合金400℃单向压缩变形过程中的晶粒尺度塑性。模拟得到的NiTi形状记忆合金变形试样的应力和应变分布表明，在晶粒尺度上存在各向异性的塑性变形。进一步利用统计存储位错密度和几何必需位错密度研究合金在单轴压缩过程中的显微组织演化。结果表明，统计存储位错用于承载塑性变形，因此其密度值随着塑性应变的增大而增大。几何必需位错在协调晶粒间变形方面起到重要作用，并且与相邻晶粒间的取向差存在关联，即在晶粒间取向差大的位置存在高的几何必需位错密度，而在晶粒间取向差小的位置出现低的几何必需位错密度。
关键词：晶粒尺度塑性；镍钛形状记忆合金；晶体塑性有限元法；塑性变形；显微组织演化
(Edited by Wei-ping CHEN)
Foundation item: Projects (51475101, 51305091, 51305092) supported by the National Natural Science Foundation of China
Corresponding author: Shu-yong JIANG, Tel: +86-13936266338, E-mail: jiangshy@sina.com; Lai-xin SHI, Tel: +86-15123376156, E-mail: shilaixin2016@cqut.edu.cn
DOI: 10.1016/S1003-6326(19)64987-3
Abstract: Grain scale plasticity of NiTi shape memory alloy (SMA) during uniaxial compression deformation at 400 °C was investigated through two-dimensional crystal plasticity finite element simulation and corresponding analysis based on the obtained orientation data. Stress and strain distributions of the deformed NiTi SMA samples confirm that there exhibits a heterogeneous plastic deformation at grain scale. Statistically stored dislocation (SSD) density and geometrically necessary dislocation (GND) density were further used in order to illuminate the microstructure evolution during uniaxial compression. SSD is responsible for sustaining plastic deformation and it increases along with the increase of plastic strain. GND plays an important role in accommodating compatible deformation between individual grains and thus it is correlated with the misorientation between neighboring grains, namely, a high GND density corresponds to large misorientation between grains and a low GND density corresponds to small misorientation between grains.
