Numerical modeling and simulation of metal powder compaction of balancer
LI Yuan-yuan(李元元), CHEN Pu-qing(陈普庆), XIA Wei(夏 伟),
ZHOU Zhao-yao(周照耀), LI Wen-fang(李文芳)
College of Mechanical Engineering, South China University of Technology, Guangzhou 510640, China
Received 9 August 2005; accepted 20 December 2005
Abstract:
The constitutive relation of powder material was derived based on the assumption that metal powder is a kind of elasto-plastic material, complying with an elliptical yield criterion. The constitutive integration algorithm was discussed. A way to solve the elastic strain increment in each iteration step during elasto-plastic transition stage was formulated. Different integration method was used for elastic and plastic strain. The relationship between model parameters and relative density was determined through experiments. The model was implemented into user-subroutines of Marc. With the code, computer simulations for compaction process of a balancer were performed. The part is not axisymmetric and requires two lower punches and one upper punch to form. The relative density distributions of two design cases, in which different initial positions of the punches were set, were obtained and compared. The simulation results indicate the influence of punch position and movement on the density distribution of the green compacts.
Key words:
balancer; powder compaction; numerical simulation; finite element; mechanical model;
1 Introduction
“Cold” compaction, which is operated at room temperature, is currently the most generally used compacting method in powder metallurgy industry. Under this circumstance, metal powder is often considered a kind of time-independent, elasto-plastic and compressible material[1,2]. Quite a few different models have been presented for such kind of material. Some of them are characterized by an ellipsoidal yield surface, such as KUHN’s[3], GREEN’s[4], SHIMA’s[5], DORAIVELU’s[6]. In some other models, ellipsoidal surface is used as a cap that composes the whole yield surface with another conic surface[7, 8]. GURSON’s, FLECK’s and REDANZ’s[2, 9] models are quite different from the elliptical models, while the shape of the yield surfaces are similar to ellipse and therefore simulation results with these models should be close to those obtained with elliptical models. Cedergren et al[10] compared the experimental results and simulation results obtained with SHIMA’s model and REDANZ’s model and concluded that, as long as the model parameters were set properly, both models could produce satisfying results. Some kinds of discreet models have also been presented and applied in simulation, while the large computation capability they require still hinders the application in the industry[11,12]. In this study, a general form of the constitutive relation of the elliptical models is derived, the numerical algorithm is described and some simulation results are discussed.
2 Theoretical basis 2.1 Constitutive relation
Since the stress state of material is independent of coordination, the yield criterion of isotropic material can be formulated by invariants of the stress tensor. A general form of yield criterion used by many investigators is
(1)
where 
is the second invariant of the deviatoric stress tensor and J1 is the first invariant of the stress tensor. A and B are the parameters of the yield surface.
Deriving Eqn.(1), yields
(2)
Let EA=?A/?ρ, EB=?B/?ρ, then Eqn.(2) can be rewritten as
(3)
Since 
[13], then
(4)
In elasto-plastic problems, when associated flowing rule is assumed, the relationship between incremental stain and stress can be expressed as
(5)
where f is the yield function and 
is the elastic constitutive tensor. Applying Eqn.(5) to Eqn.(4), and solve dλ,
(6)
Applying Eqn.(6) to Eqn.(5) yields the constitutive relation:
(7)
where
(8)
and 
is the plastic matrix, which can be expressed as
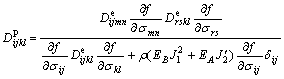(9)
2.2 Constitutive integration
As a nonlinear problem, the simulation process requires an iteration procedure to solve. One of the tasks in the iteration is to calculate the incremental stress from the incremental strain.
In each iteration step of the process, if the material transits from elastic state to plastic state, it is necessary to determine the dividing point of elastic strain and plastic strain, since different integration algorithms must be applied for them.
In the stress space, elasto-plastic dividing point is the intersection point of yield surface and the stress increment. Therefore, it can be solved from the following equations:
(10)
where 
is the stress at the beginning of the incremental step, 
is the incremental stress, and m is the percentage of the elastic strain increment in total strain increment. Applying the second equation to the first one, Eqn.(10) can be rewritten as a quadratic equation:
a2m2+a1m+a0=0 (11)
where
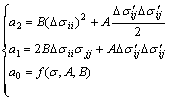(12)
where 
is the incremental deviatoric stress. Eqn.(11) has one positive and one negative root. Herein, only the positive one is concerned:
(13)
With m solved, the elastic strain and plastic strain are integrated respectively. The incremental stress in elastic stage is calculated directly,
(14)
The incremental stress in plastic stage is obtained with Eulerian formulation,
(15)
where k is the total number of integration steps.
2.3 Hardening
When powder gets denser, the yield surface also changes. This relationship can be represented by the dependency of A and B on the relative density ρ, written as A(ρ) and B(ρ).
The following relations have been presented based on the assumption that material begins to yield when the apparent total deformation energy reaches a critical value[3,6,14],
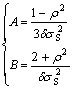(16)
where σS is the yield stress of the pore-free material and δ is a function of ρ, which should be determined on experimental results. Some of the proposals for this function are listed in Table 1.
Table 1 Different assumptions of δ(ρ)
The above model and different assumptions of δ are implemented into user subroutines of MSC.Marc, a commercial finite element analysis software. Compared the simulated and experimental load vs displacement curves, another function which fits better with the experimental results is obtained.
In simulation, the model parameters are set as σS=405 MPa, elastic modulas E=210ρ GPa and Poisson’s ratio v=0.5ρ2.
In the experiments, pure iron powders were compacted in a die with square horizontal section and side length of 10 mm. A test machine, SANS- CMT5105.7, was used to conduct the compaction. The machine is able to be connected to a computer and record the load vs displacement curves of the upper punch. The operation was described in detail in Ref.[15].
The volume of loose powder was measured and the initial relative density was calculated to be ρc=0.458. Since loose powder is quite easy to deform, the value of ρc should be very close to ρ0. In this study, it was set at 0.457 9. The friction coefficient on die walls was assumed to be 0.1.
The displacement vs load curves obtained from both experiments and simulations are compared in Fig.1.
Fig.1 Load vs displacement curves of upper punch
3 Simulation
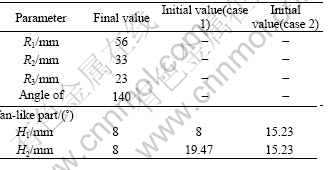
The compaction process of a balancer was simulated. The schematic plot of the die, punches and powder is shown in Fig.2. The balancer consists of two main parts: a ring to connect with the crankshaft and a fan-like part to balance the weight of the crank. The sizes of R1, R2 and R3 are constant during the compaction. H1 and H2 are controlled by punches. Their values are listed in Table 2.
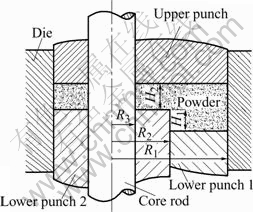
Fig.2 Cross section of die, punches and powder
Table 2 Sizes of balancer
Two design cases were simulated. In both cases, the die, lower punch 1 and core rod were fixed. In the first case, lower punch 2 was also fixed. Only the movement of upper punch densified the powder. In the second case, lower punch 2 was set at a higher position at the beginning, and moved downward along with the upper punch. The velocities of the lower punch 2 and the upper punch were proportional to the initial distances to their own final position.
The simulation was conducted on MSC.Marc. User subroutines were written and the model described above was implemented. The simulation of the two cases shared the same finite element model, with elements at the two different parts scaled in the height direction, so that initially the powder could fill the whole space in the die. Totally 10 063 four-node tetrahedral elements and 2 285 nodes were included in the model. The calculation was divided into 100 incremental steps. About six hours were spent on a PⅣ 2.4 GHz machine for each case.
The relative density distributions obtained in simulations for both cases are shown in Figs.3 and 4. In case 1, the highest relative density, 0.975, occurs at the ring part, and the lowest density, 0.570, is at the inner edge of the fanlike part. In case 2, the highest relative density, 0.904, is at the upper corner of the fanlike part, and the lowest density, 0.843, is at the lower corner of the fanlike part. Comparing the two figures, the density distribution in case 1 is much more inhomogeneous than that in case 2. This contrast shows that the first case is a bad design. In the filling stage of this design case, the initial position of lower punch 2 is too low to get sufficient powder installed into the fanlike part. And during compaction, it is difficult for the powder to flow to the ring part. Thus, there develops a density variation between the two parts.
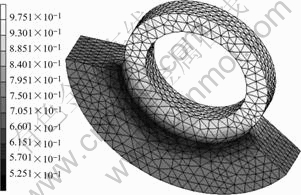
Fig.3 Relative density distribution (case 1)
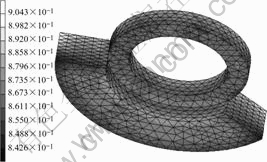
Fig.4 Relative density distribution (case 2)
4 Conclusions
1) The constitutive relation of elliptical yield criterion was derived. The constitutive integration algorithm was discussed. The relation between model parameters and relative density was determined through experiments. The model was implemented into MSC.Marc user-subroutines.
2) The compaction process of a balancer was simulated. The relative density distributions of two different design cases were obtained and compared. The simulation results show that the initial positions of the punches have great influence on the density distribution of the green compacts. To obtain homogeneous green compacts, punches should be positioned properly so that at the filling stage, sufficient powder can be installed into parts where flowing is difficult in compaction process.
References
[1] Storakers B, Fleck N A, McMeeking R M. The viscoplastic compaction of composite powders [J]. Journal of Mechanics and Physics of Solids, 1999, 47: 785-815.
[2] Redanz P. Numerical modeling of the powder compaction of a cup [J]. European Journal of Mechanics A/Solids, 1999, 18: 399-413.
[3] Kuhn h a, Downey c l. Deformation characteristics and plasticity theory of sintered powder materials[J]. International Journal of Powder Metallurgy, 1971, 7(1): 15-25.
[4] Green r j. A plasticity theory for porous solids[J]. International Journal of Mechanics Science, 1972, 14: 215-224.
[5] Shima S, Oyane M. Plasticity theory for porous metallurgy[J]. International Journal of Mechanical Sciences, 1976, 18(6): 285-291.
[6] Doraivelu s m, Gegel h l, Gunasekera j s, Malas j c, Morgan j t, Thomas Jr j f. A new yield function for compressible P/M materials[J]. International Journal of Mechanical Sciences, 1984, 26: 527-535
[7] Khoei a r, Lewis r w. Finite element simulation for dynamic large elastoplastic deformation in metal powder forming[J]. Finite Element in Analysis and Design, 1998, 30: 335-352.
[8] Lewis r w, Khoei a r. A plasticity model for metal powder forming process[J]. International Journal of Plasticity, 2001, 17: 1659-1692.
[9] Redanz p, Tvergaard v. Analysis of shear band instabilities in compaction of powders[J]. International Journal of Solids and Structures, 2003, 40: 1853-1864.
[10] Cedergren j, Sorensen n j, Bergmark a. Three- dimensional analysis of compaction of metal powder[J]. Mechanics of Materials, 2002, 34: 43-59.
[11] CHEN Pu-qing, XIA Wei, ZHOU Zhao-yao, ZHU Quan-li, LI Yuan-yuan. Three-dimensional combinedfinite-discrete element approach for simulation of the single layer powder compaction process[J]. Trans Nonferrous Met Soc China, 2004, 14: 751-755.
[12] Martin c l, Bouvard d. Study of the cold compaction of composite powders by the discrete element method[J]. Acta Materialia, 2003, 51: 373-386.
[13] Michrafy a, Ringenbacher d, Tchoreloff p. Modelling the compaction behaviour of powders: application to pharmaceutical powders[J]. Powder Technology, 2002, 127: 257-266.
[14] Kim h s, Lee d n. Power-law creep model for densification of powder compacts[J]. Mater Sci Eng A, 1999, A271: 424-429.
[15] Chen p q, Xia w, Zhou z y, Chen w p, Li y y. Three-dimensional finite element analysis of metal powder compaction[J]. Materials Science Forum, 2004, 471-472: 201-205.
Foundation item: Porject(50325516) supported by the National Natural Science Foundation of China; Project(CG2003-GA005) supported by China Education and Research Grid (China Grid); Project(003019) supported by the Natural Science Foundation of Guangdong Province, China
Corresponding author: CHEN Pu-qing; Tel: +86-20-87112933; E-mail: chpq2000@gmail.com
Abstract: The constitutive relation of powder material was derived based on the assumption that metal powder is a kind of elasto-plastic material, complying with an elliptical yield criterion. The constitutive integration algorithm was discussed. A way to solve the elastic strain increment in each iteration step during elasto-plastic transition stage was formulated. Different integration method was used for elastic and plastic strain. The relationship between model parameters and relative density was determined through experiments. The model was implemented into user-subroutines of Marc. With the code, computer simulations for compaction process of a balancer were performed. The part is not axisymmetric and requires two lower punches and one upper punch to form. The relative density distributions of two design cases, in which different initial positions of the punches were set, were obtained and compared. The simulation results indicate the influence of punch position and movement on the density distribution of the green compacts.
