文章编号:1004-0609(2016)-10-2174-07
病态整体最小二乘的迭代正则化算法
孙同贺1, 2,罗志才1, 3,姚朝龙1,宛家宽1
(1. 武汉大学 测绘学院,武汉 430079;
2. 内蒙古科技大学 矿业与煤炭学院,包头014010;
3. 武汉大学 地球空间环境与大地测量教育部重点实验室,武汉 430079)
摘 要:
当误差含变量(EIV)模型的设计矩阵病态时,采用普通整体最小二乘(TLS)算法得不到稳定的数值解。为了减弱病态性,在整体最小二乘准则的基础上附加解的二次范数约束,组成拉格朗日目标函数,推导EIV模型的正则化整体最小二乘解(RTLS)。然后将RTLS的求解转换为矩阵特征向量问题,设计一个迭代方案逼近RTLS解。通过L曲线法求得正则化因子来确定正常数,从而避免人为选择正常数的随意性。数值实例表明,提出的迭代正则化算法是有效可行的。
关键词:
EIV模型;病态问题;正则化整体最小二乘;L曲线法;正常数;
中图分类号:P207 文献标志码:A
在信号处理、计算机视觉、图像处理、通信工程以及大地测量与摄影测量等相关领域中,待求参数一般通过建立观测模型来求解。当观测系统的设计矩阵和观测量都含有误差时,便形成了误差含变量(Error-in-variables, EIV)模型。整体最小二乘(Total least squares, TLS)方法是解决EIV模型的基本途径。TLS的算法主要包括奇异值分解类算法和拉格朗日迭代算法[1-2],并扩展到加权TLS[3]以及附有等式和不等式约束的情况[4-7]。在TLS解的统计性质方面,主要研究了TLS解与LS解的关系[8],系数阵的随机误差对加权LS解[9]的影响。对TLS在测绘领域的典型应用也进行了相关研究[10]。
当设计阵的列向量间呈近似线性相关时,观测量的微小变化会引起最小二乘解的剧烈振荡,测量上一般采用截断奇异值或者Tikhonov正则化方法获得稳定的解[11-12]。根据奇异值分解,TLS解相较于LS解是一个降正则化过程,TLS解的条件数总是大于LS解的条件数[13]。GOLUB[14]提出了TLS的正则化解,给出了取不同的约束参数时,正则化整体最小二乘(Regularized total least squares, RTLS)解与TLS解的关系,并给出了一种直接算法。FIERRO等[15]给出了解RTLS的截断奇异值分解算法。SCHAFFRIN等[16]基于Gauss-Helmert模型的混合近似解理论,提出了一种新的迭代计算方案,并运用到考古学中来确定赛马场中赛道的原点和半径。BECK等[17]将RTLS问题转换成一个闭区间内的单变量函数的最小化问题。袁振超等[18]推导了等权条件下病态总体最小二乘的正则化解法。王乐详等[19]采用岭估计方法解决加权总体最小二乘平差的病态性问题,给出了确定正则化参数的岭迹法、广义交叉核实法和L曲线法。又将参数作为虚拟观测值,运用广义最小二乘准则,推导了病态总体最小二乘问题的虚拟观测解法[20]。葛旭明 等[21]提出了解RTLS的广义正则化方法。然而,在应用Tikhonov正则化方法解决病态问题时,在该方法的约束条件中需人为引入一个正常数,但是正常数的引入并没有绝对的标准,也没有一个客观的参考值,因而其值的引入存在较强的主观随意性。针对此问题,引入了误差约束的TLS正则化方法,在原有方程的基础上加入2个不等式作为约束条件[22]。GUO等[23]直接给出了RTLS迭代算法的计算公式,而没有给出详细的推导过程。这些方法均是根据观测量的精度及设计矩阵的形式人为选择设计矩阵误差上限值和正常数 ,因此具有随机性。
,因此具有随机性。
本文作者基于文献[23]中提出的RTLS的思想,详细推导了病态EIV模型的正则化解及正常数与正则化因子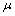 的关系,然后将RTLS的求解转换为求矩阵特征向量问题,设计了一个迭代方案逼近RTLS解。通过L曲线法求得正则化因子来确定正常数,从而避免了人为选择正常数的随意性。最后用两个算例说明了本研究所提方法的可行性和有效性。
的关系,然后将RTLS的求解转换为求矩阵特征向量问题,设计了一个迭代方案逼近RTLS解。通过L曲线法求得正则化因子来确定正常数,从而避免了人为选择正常数的随意性。最后用两个算例说明了本研究所提方法的可行性和有效性。
1 病态EIV模型的正则化方法
近年来,误差含变量(EIV)模型在测量实际中广泛出现。EIV模型采用奇异值分解算法求解时,发现它的整体最小二乘解相较于普通最小二乘解来说,法方程主对角线元素分别减去增广矩阵的最小奇异值,从而是一个降正则化(De-regularization)过程。王乐洋[13]证明了EIV模型的条件数要大于相应的线性G-M模型。因此,有必要研究EIV模型病态时的数据处理问题。
病态EIV模型可以表示为
 (1a)
(1a)
 (1b)
(1b)
式中: 为观测向量;
为观测向量;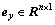 表示观测向量对应的随机误差向量;
表示观测向量对应的随机误差向量; 表示系数矩阵;
表示系数矩阵; 为未知参数向量;
为未知参数向量; 表示系数矩阵A的随机误差矩阵;e表示扩展向量
表示系数矩阵A的随机误差矩阵;e表示扩展向量 的误差向量,其中
的误差向量,其中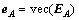 ,
,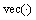 表示矩阵的拉直运算符号;
表示矩阵的拉直运算符号; 为单位权方差;矩阵
为单位权方差;矩阵 及其逆矩阵P分别表示l的协因数阵和权阵,这里假设其为单位阵,即观测向量与系数矩阵的误差向量之间独立同分布。设计矩阵A的列向量间存在近似复共线性使得观测系统病态。
及其逆矩阵P分别表示l的协因数阵和权阵,这里假设其为单位阵,即观测向量与系数矩阵的误差向量之间独立同分布。设计矩阵A的列向量间存在近似复共线性使得观测系统病态。
在测量平差理论中,通过附加一些约束信息,可以削弱系统的病态性,保证估值的稳定性。对于模型(1)所示的病态EIV模型,在观测量和系数阵误差残差最小的基础上,附加参数的二次范数约束,从而避免求解参数时因观测量的微小变动而造成解的巨大波动。其平差准则可表示成
 (2a)
(2a)
 (2b)
(2b)
 (2c)
(2c)
令A和 分别表示含观测误差和不含观测误差的系数矩阵,则
分别表示含观测误差和不含观测误差的系数矩阵,则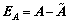 表示矩阵A的真误差。
表示矩阵A的真误差。 表示联系数向量,
表示联系数向量,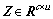 表示正则化约束条件的系数矩阵,通常是一阶或二阶差分算子,
表示正则化约束条件的系数矩阵,通常是一阶或二阶差分算子, 表示正常数。按拉格朗日乘数法原理构造函数:
表示正常数。按拉格朗日乘数法原理构造函数:
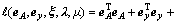
 (3)
(3)
式中: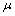 表示正则化因子,根据最优化问题的Euler-Lagrange充分条件,将式(3)分别对各变量求偏导,并令其等于0,有
表示正则化因子,根据最优化问题的Euler-Lagrange充分条件,将式(3)分别对各变量求偏导,并令其等于0,有
 (4)
(4)
 (5)
(5)
 (6)
(6)
 (7)
(7)
 (8)
(8)
式中:帽子符号表示估计值,波浪线符号表示预测值。根据式(4)和(5)可得
 (9)
(9)
 (10)
(10)
将式(9)、(10)代入式(8),即
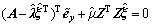 (11)
(11)
也可以表示成
 (12)
(12)
整理上式得
 (13)
(13)
将式(9)代入式(6)得
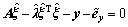 (14)
(14)
即  (15)
(15)
根据最优化理论的Kuhn-Tucker条件和有效约束的概念,可以得到:若 >0,则
>0,则 ,称为有效约束;若
,称为有效约束;若 ,则
,则 <
< 为无效约束。由此,有
为无效约束。由此,有
 >0,
>0, (16)
(16)
根据文献[1]的结论,当 过大时,若正则化矩阵为单位阵,则RTLS解和TLS解相等而使得正则化失效。因此,应该选择较小的
过大时,若正则化矩阵为单位阵,则RTLS解和TLS解相等而使得正则化失效。因此,应该选择较小的 值,使得
值,使得 成立。
成立。
另外,由式(15)可以得到
 (17)
(17)
将式(17)代入式(13),两边同时乘以 ,得
,得
 (18)
(18)
令
 (19)
(19)
 (20)
(20)
则式(18)可以简写成:
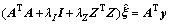 (21)
(21)
对式(8)两边同乘以 得
得
 (22)
(22)
考虑到式(7) ,式(22)又可以写成:
,式(22)又可以写成:
 (23)
(23)
由式(6)易知:
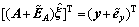 (24)
(24)
即  (25)
(25)
将式(25)代入式(23),有
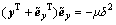 (26)
(26)
即: (27)
(27)
将式(17)代入式(27),可得
 (28)
(28)
将式(28)代入 ,简化后可得
,简化后可得
 (29)
(29)
联立式(21)和(29),可得如下的矩阵形式:
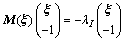 (30)
(30)
式中:
 (31)
(31)
式(21)的求解也可转换为求矩阵特征值特征向量对的问题,采用反幂法(Shifted inverse power)方法迭代求解,即求式(32)的特征向量:
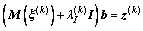 (32)
(32)
式中:k表示迭代次数,式(32)中 向量为求矩阵
向量为求矩阵 的归一化特征向量的估值:
的归一化特征向量的估值:
 (33)
(33)
定义第k次迭代的残差向量为
 (34)
(34)
当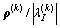 <
< 时,迭代终止。由Cauchy-Schwartz不等式和
时,迭代终止。由Cauchy-Schwartz不等式和 ,有
,有

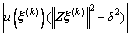 (35)
(35)
残差向量 为约束条件(16)提供了上限估计,如果
为约束条件(16)提供了上限估计,如果 足够地接近
足够地接近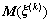 的特征向量,则式(35)的不等式约束条件可由等式取代。
的特征向量,则式(35)的不等式约束条件可由等式取代。
在迭代的过程中,确定正则化参数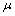 的主要步骤
的主要步骤
为:选择不同的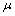 值,以
值,以 为横坐标,
为横坐标, 为纵坐标画图,得到一系列的点(
为纵坐标画图,得到一系列的点( ),
),
经过拟合得到一条L曲线,以L曲线上曲率最大的那个点对应的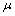 值作为最终的正则化参数。
值作为最终的正则化参数。
下面给出本研究所提方法的迭代步骤:
1) 给定约束阵Z,按照上述方法确定正则化因子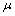 ,根据式(21)得到正则化整体最小二乘解;
,根据式(21)得到正则化整体最小二乘解;
2) 根据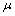 与
与 存在如式(28)所示的函数关系,确定正常数
存在如式(28)所示的函数关系,确定正常数 ;
;
3) 给定 的初值,根据式(19),(20),(33)分别计算
的初值,根据式(19),(20),(33)分别计算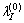 、
、 和
和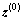 ;
;
4) 解 ,得到
,得到
 。其中,
。其中, 表示
表示 维b向量去掉最后一个元素取前面n个元素形成的向量,b(n+1)是指b向量的第n+1个元素;
维b向量去掉最后一个元素取前面n个元素形成的向量,b(n+1)是指b向量的第n+1个元素;
5) 按照步骤3的方法重新计算 和
和 ,计算
,计算 ,按照式(34)计算
,按照式(34)计算 。如果
。如果 <
< ,则终止迭代。
,则终止迭代。
2 算例分析
算例1:算例摘自文献[24],模型的设计矩阵和观测值分别为
 ,
,

经计算,法方程的条件数为cond =1.289 2×105,可见观测方程系数矩阵严重病态。未知参数5个,且真值已知,即
=1.289 2×105,可见观测方程系数矩阵严重病态。未知参数5个,且真值已知,即
 。使用Matlab分别对观测值L和设计矩阵A的每一个元素添加均值为0,方差为
。使用Matlab分别对观测值L和设计矩阵A的每一个元素添加均值为0,方差为 的随机误差,即
的随机误差,即 ,
,
 ,其中
,其中 。为了比较不同方法解的差异,分别采用最小二乘法(LS),正则化最小二乘法(RLS),整体最小二乘法(TLS),正则化整体最小二乘法(RTLS),文献[22]方法及本方法进行参数解算,其中
。为了比较不同方法解的差异,分别采用最小二乘法(LS),正则化最小二乘法(RLS),整体最小二乘法(TLS),正则化整体最小二乘法(RTLS),文献[22]方法及本方法进行参数解算,其中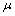 为正则化因子,
为正则化因子, 为设计矩阵误差的上限,正则化约束条件的系数矩阵Z取为单位阵,并计算不同方法所得到的结果
为设计矩阵误差的上限,正则化约束条件的系数矩阵Z取为单位阵,并计算不同方法所得到的结果 与真值
与真值 的差值范数
的差值范数 ,计算结果见表1,图1给出了本方
,计算结果见表1,图1给出了本方
法得到的L曲线图,以 为横坐标,
为横坐标,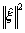 为纵坐标。
为纵坐标。
算例2:采用一组病态空间测边网的算例,同时运用不同方法进行解算,进而探讨本方法在测量数据处理中的可行性。
表1 模型参数X的计算结果
Table 1 Results of model parameter X

模拟的空间测边网算例,P1、P2、…P9为9个已知点,其坐标具体数据可参考文献[22]。9个已知点到两个未知点P10、P11的观测距离也给出,假设两个未知点真值坐标为(0,0,0)和(7,10,-5),它们之间的观测距离为d10,11=13.1078 m,各距离为等精度观测,测距中误差为±0.001 m。要求根据19个边长观测值确定两个未知点的坐标。
经计算,该测边网观测方程的系数矩阵A严重病态,法方程的条件数为4.5886×103。在计算中,两个未知点的坐标近似值分别取为(0.01,-0.01,0.02)和(7.01,9.99,-5.01)。由文献[22]可知,设计矩阵误差上限 可根据观测量的精度确定,并在此基础上略有加大。表2给出了各种算法的参数估计结果及与真值的差值范数,图2给出了本方法得到的L曲线图,横纵坐标轴同图1。
可根据观测量的精度确定,并在此基础上略有加大。表2给出了各种算法的参数估计结果及与真值的差值范数,图2给出了本方法得到的L曲线图,横纵坐标轴同图1。
通过公式推导及计算分析,可以得出如下结论:
1) 由式(27)可知,正常数与正则化因子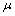 存在等式关系,因此可先利用L曲线法确定正则化因子
存在等式关系,因此可先利用L曲线法确定正则化因子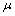 ,然后根据它们之间的等式关系确定正常数,这样可以有效地避免因正常数
,然后根据它们之间的等式关系确定正常数,这样可以有效地避免因正常数 的选择不当造成的影响;
的选择不当造成的影响;
2) 由表1和表2的统计结果可知,当系数矩阵A病态时,整体最小二乘解与真值的差值范数分别为6.7190和22.2787,较最小二乘解与真值的差值范数1.3088和10.4867要大,说明整体最小二乘解受病态的影响更为严重;
3) 采用文献[22]方法,设计矩阵误差上限取不同值,得到的解与真值的差值范数分别为(0.8253,0.8257,0.8262)和(0.0925,0.0932,0.0938);采用本研究方法得到的解与真值的差值范数分别为0.8234和0.0932。当选择较为合适的正常数时,文献[22]中的方法和本研究方法解算结果相当,但如果正常数选择不合理,结果将有较大的偏差;
表2 模型参数X的计算结果
Table 2 Results of model parameter X


图1 L曲线(算例1)
Fig. 1 L curve (Example 1)

图2 L曲线(算例2)
Fig. 2 L curve (Example 2)
4) 在正则化最小二乘算法和正则化整体最小二乘算法中,通常假设正常数 足够小,计算过程中忽略了
足够小,计算过程中忽略了 的确切值。本研究在迭代过程中考虑了
的确切值。本研究在迭代过程中考虑了 的确切值。从解与真值的差值范数看,正则化整体最小二乘算法较之本研究方法得到的结果分别有0.0056和0.0038的偏差,这主要是因为正常数
的确切值。从解与真值的差值范数看,正则化整体最小二乘算法较之本研究方法得到的结果分别有0.0056和0.0038的偏差,这主要是因为正常数 带来的影响;
带来的影响;
5) 算例2中给定的初值并不理想,但利用本研究方法得到的解算结果要好于RLS和RTLS,由此说明本研究方法对初值精度的要求不高,推广了该方法的使用。
3 结论
1) 当EIV模型设计矩阵病态时,普通的整体最小二乘算法得不到稳定的解。在观测量和系数阵误差残差最小的基础上,附加参数的二次范数约束,推导了病态整体最小二乘的迭代正则化算法,以及正常数与正则化因子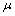 的等式关系,采用shifted inverse power算法,将RTLS的求解转换为求矩阵的特征向量问题。
的等式关系,采用shifted inverse power算法,将RTLS的求解转换为求矩阵的特征向量问题。
2) 相比已有的正则化整体最小二乘算法,本研究提出的方法有两个优势:首先,在迭代过程中考虑了 的确切值;其次,通过L曲线法求得正则化因子
的确切值;其次,通过L曲线法求得正则化因子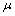 来更合理地确定正常数
来更合理地确定正常数 ,从而避免了不恰当地选取正常数,可能导致参数解存在较大偏差的情况。
,从而避免了不恰当地选取正常数,可能导致参数解存在较大偏差的情况。
REFERENCES
[1] van HUFFEL S, VANDEWALLE J. The total least squares problem computational aspects and analysis[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1991.
[2] GOLUB G H, van LOAN C F. An analysis of the total least squares problem[J]. SIAM Journal on numerical analysis, 1980, 17(6): 883-893.
[3] FANG Xing. Weighted total least squares solutions for applications in geodesy[D]. Hannover: Doctor’s Dissertation in Leibniz University, 2011.
[4] SCHAFFRIN B. A note on constrained total least-squares estimation[J]. Linear algebra and its applications, 2006, 417: 245-258.
[5] SCHAFFRIN B, FELUS Y A. An algorithmic approach to the total least-squares problem with linear and quadratic constraints[J]. Studia Geophysica et Geodaetica, 2009, 53: 1-16.
[6] ZHANG Song-lin, TONG Xiao-hua. A solution to EIV model with inequality constraints and its geodetic applications[J]. Journal of geodesy, 2013, 87: 23-28.
[7] FANG Xing. On non-combinatorial weighted total least squares with inequality constraints[J]. Journal of geodesy, 2014, 88: 805-816.
[8] van HUFFEL S, VANDEWALLE J. Algebraic connections between the least squares and total least squares problems[J]. Numerische Mathematik, 1989, 55: 431-449.
[9] XU Pei-liang, LIU Jing-nan. Effects of errors-in-variables on weighted least squares estimation[J]. Journal of Geodesy, 2014, 88: 705-716.
[10] 周拥军, 邓才华. 线性EIV模型的TLS估计及其典型应用[J]. 中国有色金属学报, 2012, 22(3): 948-953.
ZHOU Yong-jun, DENG Cai-hua. Extended total least squares problems for linear errors-in-variables model and its typical applications[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(3): 948-953.
[11] XU Pei-liang. Truncated SVD methods for discrete linear ill-posed problems[J]. Geophysical Journal International, 1998, 135: 505-514.
[12] TIKHONOV A N. Solution of incorrectly formulated problems and the regularization method[J]. Soviet Math Dokl, 1963, 4: 1035-1038.
[13] 王乐洋. 总体最小二乘解性质研究[J]. 大地测量与地球动力学, 2012, 32(5): 48-52.
WANG Le-yang. Research on properties of total least squares estimation[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 48-52.
[14] GOLUB G H, HANSEN P C, O’LEARY D P. Tikhonov regularization and total least squares[J]. SIAM Journal on Matrix Analysis and Applications, 1999, 21(1): 185-194.
[15] FIERRO R D, GOLUB G H, HANSEN P C. Regularization by truncated total least squares[J]. SIAM Journal on Scientific Computing, 1997, 18(1): 1223-1241.
[16] SCHAFFRIN B, SNOW K. Total least-squares regularization of Tykhonov type and an ancient racetrack in Corinth[J]. Linear Algebra and Its Applications, 2010, 432: 2061-2076.
[17] BECK A, BEN-TAL A. On the solution of the Tikhonov regularization of the total least squares problem[J]. SIAM Journal on Optimization, 2006, 17(1): 98-118.
[18] 袁振超, 沈云中, 周泽波. 病态总体最小二乘模型的正则化算法[J]. 大地测量与地球动力学, 2009, 2(2): 131-134.
YUAN Zhen-chao, SHEN Yun-zhong, ZHOU Ze-bo. Regularized total least squares solution to ill-posed error-in- variable model[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 131-134.
[19] 王乐洋, 许才军, 鲁铁定. 病态加权总体最小二乘平差的岭估计方法[J]. 武汉大学学报信息科学版, 2010, 35(11): 1346-1350.
WANG Le-yang, XU Cai-jun, LU Tie-ding. Ridge estimation method in ill-posed weighted total least squares adjustment[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1346-1350.
[20] 王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581.
WANG Le-yang, YU Dong-dong. Virtual observation method to ill-posed total least squares problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575-581.
[21] 葛旭明, 武吉仓. 病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3): 372-377.
GE Xu-ming, WU Ji-cang. Generalized regularization to ill-posed total least squares problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 372-377.
[22] 葛旭明, 武吉仓. 误差限的病态总体最小二乘解算[J]. 测绘学报, 2013, 42(2): 196-202.
GE Xu-ming, WU Ji-cang. A regularization method to ill-posed total least squares with error limits[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 192-202.
[23] GUO Hong-bin, RENAUT R A. A regularized total least squares algorithm[C]// Total Least Squares and Errors-in-Variables Modeling. Copenhagen: Kluwer Academic Publishers, 2002: 57-66.
[24] 鲁铁定, 宁津生. 总体最小二乘平差理论及其应用[M]. 北京: 中国科学技术出版社, 2011.
LU Tie-ding, Ning Jin-sheng. Total least squares adjustment theory and its applications[M]. Beijing: China Science and Technology Press, 2011.
Iterative and regularized algorithm to ill-posed total least squares
SUN Tong-he1, 2, LUO Zhi-cai1, 3, YAO Chao-long1, YUAN Jia-kuan1
(1. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
2. Mining and Coal Institute, Inner Mongolia University of Science and Technology, Baotou 014010, China;
3. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education,
Wuhan University, Wuhan 430079, China)
Abstract: When the design matrix of errors-in-variables (EIV) model was ill-conditioned, the ordinary total least squares (TLS) solution was unstable. In order to weaken the ill-conditioning, an Euclid norm constraint of the solution was added to the TLS minimization rule. Then, the Lagrange objective function was formed and the regularized total least squares (RTLS) solution was deduced. Afterwards, the RTLS was transformed to a problem of looking for a matrix’s eigenvector. An iterative program was designed to approximate the solution. The L-curve method was used to choose the regularization factor to determine the positive constant, which can avoid the subjective decision. The simulations show the efficiency and feasibility of the algorithm.
Key words: EIV model; ill-posed problem; regularized total least squares; L-curve method; positive constant
Foundation item: Project(41474006) supported by the National Natural Science Foundation of China
Received date: 2015-12-04; Accepted date: 2016-04-10
Corresponding author: SUN Tong-he; Tel: +86-472-5951692; E-mail: suntonghe202@163.com
(编辑 王 超)
基金项目:国家自然科学基金资助项目(41474006)
收稿日期:2015-12-04;修订日期:2016-04-10
通信作者:孙同贺,讲师,博士;电话:0472-5951692;E-mail: suntonghe202@163.com
摘 要:当误差含变量(EIV)模型的设计矩阵病态时,采用普通整体最小二乘(TLS)算法得不到稳定的数值解。为了减弱病态性,在整体最小二乘准则的基础上附加解的二次范数约束,组成拉格朗日目标函数,推导EIV模型的正则化整体最小二乘解(RTLS)。然后将RTLS的求解转换为矩阵特征向量问题,设计一个迭代方案逼近RTLS解。通过L曲线法求得正则化因子来确定正常数,从而避免人为选择正常数的随意性。数值实例表明,提出的迭代正则化算法是有效可行的。
[10] 周拥军, 邓才华. 线性EIV模型的TLS估计及其典型应用[J]. 中国有色金属学报, 2012, 22(3): 948-953.
[13] 王乐洋. 总体最小二乘解性质研究[J]. 大地测量与地球动力学, 2012, 32(5): 48-52.
[18] 袁振超, 沈云中, 周泽波. 病态总体最小二乘模型的正则化算法[J]. 大地测量与地球动力学, 2009, 2(2): 131-134.
[19] 王乐洋, 许才军, 鲁铁定. 病态加权总体最小二乘平差的岭估计方法[J]. 武汉大学学报信息科学版, 2010, 35(11): 1346-1350.
[20] 王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581.
[21] 葛旭明, 武吉仓. 病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3): 372-377.
[22] 葛旭明, 武吉仓. 误差限的病态总体最小二乘解算[J]. 测绘学报, 2013, 42(2): 196-202.


