Influence of melt-treatment on material constants of aluminum sheet used for easy-open can during hot deformation
CHEN Yong-lu(陈永禄), FU Gao-sheng(傅高升), CHEN Wen-zhe(陈文哲)
College of Materials Science and Engineering, Fuzhou University, Fuzhou 350002,China
Received 12 June 2005; accepted 19 December 2005
Abstract:
The isothermal compression test at elevated temperature was carried out for aluminum sheets prepared by different melt-treatment methods with aid of dynamic hot/mechanical simulation experimental technology. The material constants of hot deformation have been solved by multivariate regression directly. Influence of metallurgy factors on the constants was analyzed. The results show that at some strain, the relationship of sheets’ flow stress with deformation temperature and strain rate can be expressed more suitably with Arrhenius equation modified by hyperbolic sine function. Structure factor A1, stress-level coefficient α, strain rate sensibility exponent m and deformation activation energy Q all increase with increment of strain, while stress exponent n decreases gradually. The bigger α value or the smaller n value is, the more obvious the dynamic softening is, but the α value will increase for the metallurgy defects existing in the sheets. Influence of melt-treatment on Q depends upon the synthesis effect of all kinds of metallurgy defects. The Q and n values of the sheet prepared by high-efficient melt-treatment are the least, while the m value is the biggest, and the sheet can deform easily and evenly.
Key words:
aluminum sheet; easy-open can; material constants; melt-treatment; hot compression deformation;
1 Introduction
The sheets (especially can body sheet) used for easy-open can adopted in China still rely greatly on import at present[1]. Only some kinds of domestic-made sheets reach the quality standard, so the sheets can only support for lids making in a large amount and are less likely to be used for the can body[2]. People pay more concerns on the role of hot-rolling equipment and control technology of rolling on improving quality of the sheets during long-term research and production practices, but the effect of ingots’ metallurgical quality on hot-rolled product quality is often ignored. The study on essential connection of the two factors has been less reported yet. Only the functional relationships of flow stress of the corresponding aluminum sheets with Z parameter have been established in the research of flow stress of hot compression of numerous aluminum sheets[3-7]. And the relationship of the sheet with the hot deformation material constants calculated from each stress equation has not been formulated yet. On the basis of the studies at earlier stage[8, 9], the hot compression test for the aluminum sheets prepared by different melt-treatment methods will be carried out with an aid of dynamic hot/mechanical simulation experimental technology. The material constants of different sheets deformed at different strain have been calculated by multivariate regression. The functional relationship between peak flow stress(σp) of the sheets and the main hot deformation conditions(T, 
) can be set up, thus providing experimental basis for the actual rolling control.
2 Experimental
Cylindrical hot simulation samples with the dimensions of d 10 mm×15 mm have been machined from the aluminum ingots prepared by different melt-treatment methods[9]. Flat grooves were milled in both terminal surfaces of sample for depositing lubricant. The corresponding sample code names were: WTC was prepared by no melt-treatment, NTC was prepared by routine melt-treatment, HTC was prepared by high- efficient melt-treatment. The axial-symmetry isothermal hot compression test has been carried out by means of he Gleeble-1500 type dynamic hot/mechanical simulation testing machine. The deformation temperature and strain rate are within the range of 573-773 K and 0.01-10.0 s-1, respectively, and the deformation amount is 50% (ε≈0.7). The samples are heated by utilizing its own resistance at speed of 200 K/min, and held at the setting temperature for 3 min before deformation. The samples are quenched with water immediately after deformation, which is to keep the real structure of hot deformation at elevated temperature. The validity of the test has been judged according to Ref.[10] because of existing “bulge” on the samples compressed. The true stress—true strain curves are drawn and regression analysis is carried out by using software EXCEL.
3 Solution method of hot deformation material constants
During hot deformation of metals, flow stress(σ) value depends on deformation temperature(T), strain rate(), strain(ε) and structure characteristic, such as ingredient, grain size and deformation history before deformation. Owing to the complex influence of structure, in general, only the effect of hot deformation conditions are taken into account. So flow stress(σ) can be expressed as
(1)
The concrete form of Eqn.(1) varies with materials and the type of hot deformation.
Zener and Hollomon put forward one new method to describe flow stress at elevated temperature with the parameter Z including T and 
, by means of steel’s high-speed tensile test[11], that is,
(2)
At a definite strain, Eqn.(2) is further expressed as
(3)
where Z is Zener-Hollomon parameter, so-called “temperature-compensated strain rate factor”; Q, T and R are hot deformation activation energy (J/mol), absolute temperature(K) and gas constant, respectively.
On this basis, Sellars and his co-workers[12] described the relations mentioned above with Arrhenius relation that has been amended and contained hot deformation activation energy Q, that is,
(4)
Then
(5)
Two expressions of different stress levels can be obtained by Taylor series expansion[13] in Eqn.(5),
For low stress level:
(6)
For high stress level:
(7)
where A1, A2, A3, α, β, n and m′ are all material empirical constants. Among them, α and n are stress-level coefficient (mm2/N) and stress exponent, respectively, and β=α/n. m′ is the reciprocal of strain rate sensibility exponent(m), namely m=1/m′.
At the same strain, the same material has different stress levels under different deformation conditions. It is usually supposed that the material flow stress at elevated temperature all satisfy Eqns.(5)-(7), correlation of those is judged by regression, and the best one is chosen finally. It is also generally acknowledged that Eqn.(5) is suit for all the stress levels, and the reason of calculation for Eqns.(6) and (7) is to obtain m′ and β. The traditional graphical method of solving the material constants is comparatively tedious. Although more accurate constants can be solved by means of iteration considering from mathematic methods, the corresponding iteration program is needed to write for calculation and the method is on the base of the calculation by graphical method. Therefore, the multivariate regression method for solving the constants directly is proposed in this paper and the solving process is simplified. Then, the natural logarithm types of Eqns.(5)-(7) are as follows:
(8)
(9)
(10)
The values of Q solved are different because of the difference of stress level prerequisites in Eqns.(8)-(10). In this paper, the Q value in Eqn.(8) is chosen as the hot deformation activation energy of the material and the value of A1 is further regarded as the structure factor of the material.
4 Results
4.1 Flow stress curves and peak value of flow stress
Influences of hot deformation conditions on the true stress—true strain curves of sheets used for easy-open can prepared by different melt-treatment methods are shown in Fig.1. Ref.[14] pointed out that flow stress in Eqn.(4) was saturation stress, and generally was substituted with peak stress (σp) or steady state stress(σs) when calculating. However, steady state stress is influenced greatly by measurement precision and the materials have not yet entered the steady state deformation fully under some experimental conditions, so the peak values shown in Tables 1 and 2 are selected as calculation.
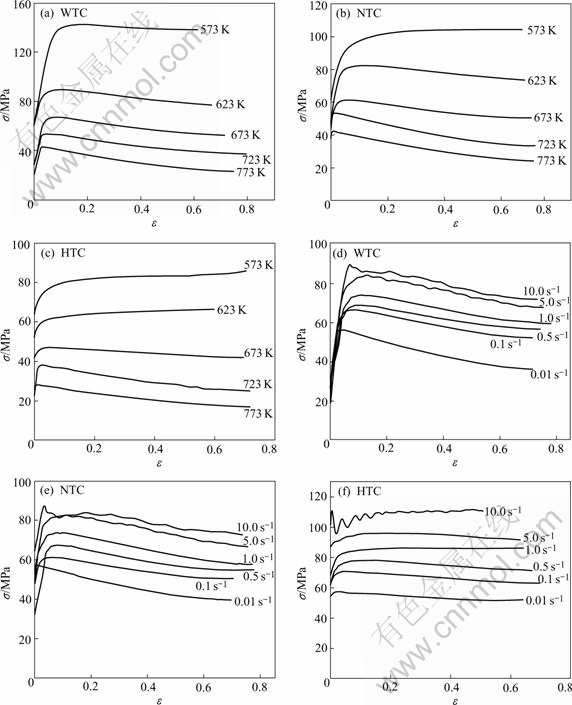
Fig.1 Features of σ—ε curves of aluminum sheets used for easy-open can and prepared by different melt-treatment methods under different hot deformation conditions: (a)-(c) Influence of temperature (
=0.1 s-1); (d)-(f) Influence of strain rate (T=673 K)
4.2 Solution results of material constants of hot deformation
The regression results show that remarkable credibility can be obtained by multivariate regression according to Eqns.(8)-(10) for aluminum sheets prepared by different melt-treatment methods; the multiple correlation coefficients (r2) are all bigger than 0.92 and the values of F are all bigger than the value of F0.01(2,7). In addition, the regression credibility of Eqn.(8) is the most notable of all (r2＞0.94). Therefore, it is indicated that at some strain, the relation of flow stress of the sheets at elevated-temperature with deformation temperature, strain rate can be expressed more suitably with the Arrhenius equation modified by hyperbolic sine function. The results of multivariate regression according to Eqn.(8) by adopting peak flow stress of sheets under different hot deformation conditions are listed in Table 3, and the corresponding hot deformation material constants are listed in Table 4.
Table 1 Peak flow stress of aluminum sheets used for easy-open can and prepared by different melt-treatment methods at strain rate of 0.1 s-1 and within 573-773 K(MPa)
Table 2 Peak flow stress of aluminum sheets used for easy-open can and prepared by different melt-treatment methods at 673 K and within 0.01-10.0 s-1(MPa)
As to the aluminum sheets used for easy-open can with the same composition, the material constants have obvious difference because of different melt-treatment methods. The sheet prepared by high-efficient method (HTC) has the maximum value of m and the minimum values of α, β, n, A1 and Q. For NTC and WTC, many values of material constants are relatively close. And WTC has the maximum value of hot deformation activation energy.
4.3 Influence of strain on material constants of hot deformation
Eqn.(3) is derived from Eqn.(2) at certain strain, so the regression results above can only indicate the characteristics of hot deformation of the sheets near the peak stress. Refs.[15, 16] have showed that the laws of flow stress at any moment of hot deformation varying with deformation temperature(T) and strain rate() could be well described with Eqns.(8)-(10). Therefore, in order to preferably study the variable law of flow stress of the sheets during the whole hot deformation, the values of flow stress at different strains (ε=0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6) and different hot deformation conditions are obtained from the σ—ε curves for different sheets, the multivariate regressions will be carried out with Eqns.(8)-(10) according to these values. The credibility of regression results is more remarkable for all the regression equations after the significance inspection, that is, r2＞0.93 and F＞F0.01(2,7). The influences of strain on the main material constants of hot deformation of the aluminum sheets are shown in Fig.2.
From Fig.2 the following can be known.
1) Fluctuation extent of stress level coefficient (α) of the sheets prepared by different melt-treatment methods is small and that of HTC hardly changes while ε＜0.2, and the α values of different sheets have a tendency to rise gradually with the further increasing of strain (Fig.2(a)). The strain(ε) corresponding to the peak stress under most deformation conditions is less than 0.2, so it is considered that the increment of α after ε＞0.2 relates to the predominance of the sheets’ dynamic softening after the peak stress. During the whole deformation, α value of HTC is the minimum.
2) The range of reduction of the n value decreases while the strain approaches steady state, because of the relatively full recrystallization of the sheets. The n value of HTC is also the minimum all along the whole deformation.
3) The strain rate sensitive coefficient (m) increases gradually with the increasing strain. The m value of WTC is relatively close to that of NTC, and both are much smaller than that of HTC, which proves that the material structure is the main reason for influencing homogeneity of hot deformation.
4) the hot deformation activation energy (Q) of WTC or NTC increases with the increment of strain. It is indicated that the increment of strain will raise the material’s energy barrier during hot deformation. The sample of WTC is relatively difficult to deform when subjected to the same load, since its Q value is the largest of all in the initial stage of deformation. When the sheets are deformed while the strain is more than 0.4, the Q value of WTC is larger than that of routine melt-treatment. And Q value of HTC is the smallest of all and nearly invariable, therefore the material deforms easily.
Table 3 Results of multivariate regression with peak flow stress of aluminum sheets used for easy-open can and prepared by different melt-treatment methods
Table 4 Hot deformation material constants of aluminum sheets used for easy-open can and prepared by different melt-treatment methods
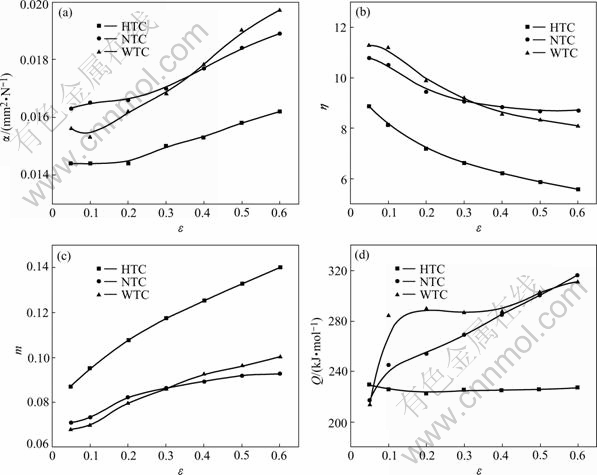
Fig.2 Relations among strain and material constants of hot deformation of aluminum sheets prepared by different melt-treatment methods: (a) σ—ε; (b) n—ε; (c) m—ε; (d) Q—ε
All the material constants obtained above relate to the strain. Consequently, a new approach of establishing the equation of flow stress at elevated temperature of the material can be acquired by setting up the functional relationship of the constants and the strain, and incorporating the relational model of flow stress and hot deformation conditions at the certain strain.
5 Analysis and discussion
5.1 Influence of melt-treatment on stress level coefficient and stress exponent of aluminum sheets
It is known that the stress level coefficient(α) and stress exponent(n) can be used for characterizing the trend of dynamic softening of aluminum sheets during hot deformation by considering the flow stress curves and corresponding material constants calculated both in this paper and Ref.[17], that is, the larger the α value is or the smaller the n value is, the more obvious the dynamic softening is. However, the α and n values are only the mechanical characteristic values during hot deformation, and the influence of the structure is not considered. Influence of metallurgical defects on hot deformation properties of aluminum sheet is a quite complicated subject, which is concerned with defects’ origin, kinds, distribution state, quantity and other uncontrolled factors. Therefore, the obvious dynamic softening of the aluminum sheets with different metallurgical qualities during hot deformation can not be explained only by the predominance of dynamic recrystallization or strong dynamic recovery. Furthermore, the role of metallurgical factors should be taken into account.
Influence of melt-treatment on the metallurgical quality and the main mechanical properties of the sheets at room temperature has been studied systematically in Ref.[9]. The structure and property of HTC are so ideal that the flow stress level of HTC is still higher than those of the other sheets under the same hot deformation conditions. However, the contents of inclusions or gas are higher in WTC or NTC, and the grain size of them is bigger too, and distributes non-uniformly. The remarkable metallurgical defects in the aluminum sheets, such as the coarse inclusions, shrinkage porosity and gas pores, will destroy the continuity of the matrix and make internal stress of sheets increase under the compressive stress, thus resulting in stress concentration and finally initiating local crackle, which lowers the material properties on the whole. Certainly, the surfaces of the coarse inclusions or second phases can also become the nucleation bases of recrystallization, but these defects have little effect on accelerating the dynamic recrystallization softening, because of their relatively tiny content and misdistribution. Consequently, it can be partly considered that the role of metallurgical defects makes WTC or NTC take on the curve feature of obvious dynamic recrystallization and the larger 
value during hot deformation. Due to effect of the metallurgical defects, microcracks will likely initiate in the sheets while reaching the strain corresponding to peak stress, because of stress concentration and other reasons, and which will lead to the increment of flow stress reduction amplitude in the course of softening stage. When the deformation temperature increases somewhat, the flow stress of the samples drops by large amplitude, which can be seen in the curve of WTC at 623 K.
5.2 Influence of melt-treatment on hot deformation activation energy of aluminum sheets
Combining the as-cast structure and the feature of σ—ε curves of the experimental materials, it can be concluded that the hot deformation activation energy(Q) is a physical quantity like the elevated- temperature flow stress(σ) that depending on the hot deformation conditions(T,, ε) and material structure.
The hot deformation activation energy(Q) can be used to characterize the ability of hot deformation. In general, the Q value of the material is larger, its hot deformation is more difficult. The essence of plastic deformation is the movement and interaction of dislocations. So, various kinds of metallurgical defects of the aluminum sheets that influence the movement of dislocations during hot deformation will be sure to influence the Q value. The high content and relatively coarse size of inclusions(Al2O3) and the thick-needle phases precipitating in the grain boundary[9] existing in WTC, will hinder the movement of dislocations seriously during hot deformation, and increase the energy needed for slipping or climbing of the dislocations, thus increasing the Q value. From the point of the diffusion of solute atoms, the hot deformation is proceeding with dynamic precipitation and solid solution, so the distribution of solute atoms will influence Q value. The solution atoms(Mg) are difficult to diffuse fully and easy to aggregate and form the air mass in WTC or NTC, which will raise the chemical drag force against the dislocation network or the single one[18], so the Q value increases. In addition, the grains with smaller size of the sheets will reduce the Q value generally. Hence, melt-treatment is one of the main intrinsic factors influencing the Q value of the sheet used for easy-open can, and the influence extent of melt-treatment on Q is the result of synthetic effect of the metallurgical defects.
According to the Q values, the obvious feature of dynamic softening of the curves of WTC or NTC has the internal relationship with the metallurgical defects of the materials. Therefore, it is difficult to reflect the hot plastic characteristics accurately only according to the feature of the curves. The structure feature of hot deformation and other testing measures should be considered yet to reflect the feature of hot deformation better.
5.3 Influence of melt-treatment on strain rate sensibility exponent of aluminum sheets
In the sense of physics, the increasing velocity of flow stress will be accelerated with increasing strain, provided that the strain rate sensibility exponent(m) is larger[19]. As to compression deformation, if the sectional sample deforms relatively heavily, the strain rate of the section will be accelerated, which will hinder the deformation and improve the the flow stress of the material keeping on deforming. Accordingly, the larger value of can improve uniformity of the material and enhance the performance of hot plastic deformation. The m value of the sample prepared by high-efficient method during the whole deformation is greater than that of sample prepared either without melt-treatment or by routine method and the m values of WTC or NTC sample are approximate in this experiment. The main reasons lie in that the purity of the aluminum sheet has been improved by the high-efficient purification of aluminum melt, which has reduced the grain size at the same refining treatment and improved the effect of modification, so the relatively homogeneous structure can be obtained. It is one of the causes that the Q value of HTC fluctuates a little during the whole hot deformation. It can also be found from the macroscopic state of the samples that the flank of WTC is not smooth after compression, that is, undulating slightly, even at higher temperature (773 K). That is the macro-feature of non- homogeneous deformation of materials. Though the metallurgical defects in NTC are less than that in WTC, the relatively rough flanks still appear on the most samples compressed. And sections of HTC deform evenly and improve the surface quality of the samples, which is in favor of the subsequent deformation processes.
6 Conclusions
1) The relationship of flow stress(σ) of the sheets prepared by different melt-treatments and deformed at some strain(ε) with deformation temperature(T), strain rate() can be expressed more suitably with the Arrhenius equation modified by hyperbolic sine function. And the material constants of hot deformation can be solved by multivariate regression directly.
2) The hot deformation material constants are influenced by strain. Namely, the values of structure factor(A1), stress level coefficient(α), strain rate sensibility exponent(m) and the hot deformation activation energy(Q) increase, and the value of stress exponent(n) decreases with the increment of the strain. In addition, the Q value of HTC changes little during the whole deformation.
3) The α and n values can be used to characterize the trend of dynamic softening of the aluminum sheets during hot deformation, that is, the larger the α value is or the smaller the n value is, the more obvious the dynamic softening is. But both constants are only the mechanical characteristic values for describing the hot deformation, and structure analyzing should be taken into account while studying the apparent mechanical behaviors. Therefore, the m value of HTC during the whole deformation is greater than that of other samples and the sheet takes on the favorable properties of even deformation.
4) The extent of the influence of melt-treatment on Q is the result of synthetic effect of the metallurgical defects. The Q value can be used to characterize the ability of hot deformation. At the peak stress, the Q values of the three sheets are different, that is, 304.72 kJ/mol for WTC, 273.95 kJ/mol for NTC and 221.24 kJ/mol for HTC. The Q value of HTC is the smallest during the whole deformation and makes the sheet deform easily.
References
[1] ZHANG Wen-can. Resent situation, progress and development suggestion of metal packaging material for food and can making industry at home and abroad[J]. Food and Fermentation Industries, 2000, 27(1): 69-73.(in Chinese)
[2] CHEN Ce, WANG Jing-hai. Advance in hot rolling technology[J]. Light Alloy Fabrication Technology, 2002, 30(4): 8-14.(in Chinese)
[3] Mcqueen H J, Fry E, Belling J. Comparative constitutive constants for hot working of Al-4.4Mg- 0.7Mn(AA5083)[J]. Journal of Material Engineering and Performance, 2001, 10(2): 164-172.
[4] Aghaie-Khafri M. Predicting flow localization and formability of aluminum alloy sheets[J]. Journal of Engineering Manufacture, 2004, 218(10): 1313-1322
[5] SHEN Jian. Material constants of an Al-Li-Cu-Mg-Zr alloy during deformation at elevated temperatures[J]. Trans Nonferrous Met Soc China, 1998, 8(1): 78-82.
[6] LIN Qi-quan, ZHANG Hui, PENG Da-shu, LIN Gao-yong, WANG Zhen-qiu. Feature of flow stress of 2519 aluminum alloy during hot compression deformation[J]. Mining and Metallurgical Engineering, 2002, 22(2): 113-116.(in Chinese)
[7] JIANG Shu-nong, LIU Chu-ming, LI Hui-zhong, ZHANG Xin-ming. Flow stress feature of 99.992% aluminum under hot compression deformation[J]. Hot Working Technology, 2004 (9): 17-19.(in Chinese)
[8] FU Gao-sheng. Study on Metallurgical Quality and Deformation Behavior of Aluminum Sheet Used for Can[D]. Changsha: Central South University of Technology, 2000, 3.(in Chinese)
[9] CHEN Yong-lu, FU Gao-sheng, CHEN Wen-zhe. Influence of high-efficient melt-treatment on the as-cast structures and properties of aluminum ingots used for easy-open can[J]. Journal of Fujian University of Technology, 2003, 1(4): 11-15, 54.(in Chinese)
[10] WANG Zhi-qiang, SHEN Jian, ZHANG Xin-ming. Study on deformation inhomogeneity of Al-Li alloy during hot compression[J]. Chinese Journal of Rare Metals, 1999, 23(6): 466-470.(in Chinese)
[11] Zerner C, Hollomon J H. Effect of strain-rate upon the plastic flow of stell[J]. J Appl Phys, 1944, 15(1): 22-27.
[12] Sellars C M, McG W J. On the mechanism of deformation[J]. Acta metall, 1966, 14: 1136-1138.
[13] Poirier J P. The High-Temperature Plastic Deformation of the Crystal[M]. GUAN De-lin, transl. Dalian: Dalian University of Science and Technology Press, 1989.(in Chinese)
[14] Lassaroui A, Jonas J J. Prediction of steel flow stress at high temperatures and strain rates[J]. Metall Trans A, 1991, 22A:1545-1558.
[15] Imbert C, Ryan N D ,McQueen H J. Hot workability of three grade of tool steel[J]. Metall Trans A, 1984, 15(10): 1855-1864
[16] Milovic C, Manojlovic D, Andjelic M, DROBNJAK D. Hot workability of M2 type high-speed steel[J]. Steel Research, 1992, 63(2): 78-84
[17] WANG Huo-sheng. The Behavior of Flow Stress and the Characteristic of Microstructure of Aluminum Sheet Used for Easy-Open Can During Deformation at Elevated Temperature[D]. Fuzhou: Fuzhou university, 2004, 2.(in Chinese)
[18] SHEN Jian. Hot deformation behavior of AA7005 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2001,11(4): 593-597.(in Chinese)
[19] WANG Da-nian. Plasticity Formation Theory of Metal [M]. Beijing: China Machine Industry Press,1984.(in Chinese)
Foundation item: Project(JA04251) supported by the Education Department of Fujian Province, China; Project(E0210011) supported by the Natural Science Foundation of Fujian Province, China
Corresponding author: FU Gao-sheng; Tel: +86-591-87893010; E-mail: fugaosheng@fzu.edu.cn
Abstract: The isothermal compression test at elevated temperature was carried out for aluminum sheets prepared by different melt-treatment methods with aid of dynamic hot/mechanical simulation experimental technology. The material constants of hot deformation have been solved by multivariate regression directly. Influence of metallurgy factors on the constants was analyzed. The results show that at some strain, the relationship of sheets’ flow stress with deformation temperature and strain rate can be expressed more suitably with Arrhenius equation modified by hyperbolic sine function. Structure factor A1, stress-level coefficient α, strain rate sensibility exponent m and deformation activation energy Q all increase with increment of strain, while stress exponent n decreases gradually. The bigger α value or the smaller n value is, the more obvious the dynamic softening is, but the α value will increase for the metallurgy defects existing in the sheets. Influence of melt-treatment on Q depends upon the synthesis effect of all kinds of metallurgy defects. The Q and n values of the sheet prepared by high-efficient melt-treatment are the least, while the m value is the biggest, and the sheet can deform easily and evenly.
