Trans. Nonferrous Met. Soc. China 26(2016) 1965-1974
Application of Hilbert-Huang transform based delay time identification in optimization of short millisecond blasting
Xiu-zhi SHI, Xian-yang QIU, Jian ZHOU, Xin CHEN, Yu-qian FAN, Er-wei LU
School of Resources and Safety Engineering, Central South University, Changsha 410083, China
Received 14 January 2016; accepted 6 June 2016
Abstract:
The accurate identification of delay time in millisecond blasting plays an important role in the optimization of blasting design and reduction of vibration effect. Through a case study of a surge shaft blasting project, the capability of the EMD (empirical mode decomposition) method in identifying the delay time of short millisecond blasting with precise initiation was compared with the instantaneous energy method based on Hilbert-Huang transform (HHT). The recognition rate of the EMD method was more than 80%, while the instantaneous energy method was less than 25%. By analyzing the instantaneous energy of single-hole blasting signal, it was found that the instantaneous energy method was adaptable to millisecond blasting with delay time longer than half of the energy peak period. The EMD method was used to identify delay time of millisecond blasting in Zijinshan open-pit mine. According to the identification results, the blasting parameters were optimized for controlling the blast-induced vibration and reducing the large block ratio. The field data showed that the velocity peak of ground vibration was reduced by more than 30% under almost the same maximum charge per delay by the optimization of delay time and detonating detonators. Combining with slag-remaining blasting and burden optimization of the first row, the large block ratio was reduced to less than 3%. The research results proved that the identification method based on HHT was feasible to optimize the blasting design. The identification method is also of certain reference value for design optimization of other similar blasting projects.
Key words:
delay time identification; short millisecond blasting; precise initiation; vibration reduction; Hilbert-Huang transform (HHT);
1 Introduction
Hard rock fragmentation by blasting is widely adopted not only in mining and quarrying, but also in underground space engineering, dam construction, and traffic engineering [1-3]. Generally, a part of energy released during blasting is utilized directly for breaking rock within target range, while the rest causes damage to the surrounding rock, structures and environment in the forms of ground vibration, noise, flying rocks, back break and air blasts [4-6]. Among all the negative effects, ground vibration effect is regarded as the head of blasting hazards which has received widespread attention from scholars and environmentalists [1-6]. It is of significant importance to strike a balance between rock fragmentation and ground vibration reduction through blasting optimization.
Millisecond blasting technique is an effective measure to reduce ground vibration and improve rock breaking by controlling the initiations time and sequences of detonators [7-9]. Determination of rational delay time for millisecond blasting is a key factor to gain favorable blasting effectiveness [10]. Due to the fact that blasting is influenced by many uncontrollable factors such as rock property, joint fracture, and nature of the terrain, determination of delay time simply by field blasting tests is costly [11,12]. In recent years, a commonly used method is to make two-stage additions in different millisecond intervals with measured single-stage signals of blast-induced vibration and the delay time is designed according to the reduction rates of superposition signals [13-15]. However, as the blasting vibration signal is a typical non-station random signal, superposition signals are really far away from the real signals [16]. Thus, a method that can optimize blasting parameters by actual vibration signal analysis is excepted.
It is recognized that the initiation time controlled by ordinary detonators has initiation errors which could lead to time-shifted or even missing detonation [17]. In order to evaluate the quality of millisecond blasting, and thus to optimize the blasting parameters, accurate identification of delay time by vibration signal analysis is highly necessary. There are a number of documents devoted to studying the delay time identification in millisecond blasting [16,18-23]. LING and LI [16] proposed a time-energy analysis method based on wavelet transform (WT) for identifying real delay time in millisecond blasting. ZHANG et al [18] used pattern adapted wavelet method to solve the issue of wavelet basis selection. QIAN and LI [19] and ZHANG et al [20] studied the instantaneous energy method and empirical mode decomposition (EMD) method based on Hilbert- Huang transform (HHT), respectively. WANG et al [21] argued that the HHT method could have higher resolution and better ability to identify the peak point of signal compared with time–energy analysis method based on GONG et al [22,23] that the identification rate of EMD method was about one third higher than that of instantaneous energy method based on HHT. Generally speaking, as the time-energy analysis method based WT is limited by the choice of wavelet-base functions, the HHT method is more frequently adopted for its preponderance in self adaptive ability.
Recently, with the increasing demand of the vibration control, conventional blasting technique with ordinary detonator detonating could hardly satisfy the security requirement [22]. High-precision detonators have been utilized widely for its high initiation accuracy and excellent security [24,25]. However, the initiation errors of high-precision nonel detonators (generally less than ±1 ms) could be accumulated gradually, especially in complicated initiation network with a large number of detonator time steps [21]. For short millisecond blasting (less than 25 ms), slight deviation of detonators could affect the blasting effect. This work comparatively studies the two HHT methods in identifying the delay time of short millisecond blasting with precise initiation. It is found that the identification rate of the EMD method is sharply higher than the instantaneous energy method. Finally, the EMD method is used to identify the delay time of millisecond blasting in an open-pit mine and the blasting parameters are optimized based on the identification results.
2 Identification method of delay time based on Hilbert-Huang transform (HHT)
2.1 Hilbert-Huang transform (HHT)
Hilbert-Huang transform (HHT) is an adaptive analysis method proposed by HUANG et al [26,27] and PENG et al [28], which includes empirical mode decomposition (EMD) and Hilbert transform. EMD could decompose non-stationary signals into a series of intrinsic mode functions (IMFs) with different scales. Each IMF expanded from a non-stationary time signal by EMD has its own physical meanings. The procedure for decomposing a signal x(t) into IMFs is as follows.
1) Get all extreme points of x(t), then construct the upper xmax(t) and lower envelope xmin(t) separately by interpolating on all maximums and minimums using cubic spline function. Similarly, calculate the mean of the upper and lower envelope:
m1(t)=[xmax(t)+xmin(t)]/2 (1)
2) Get h(t) by subtracting m1(t) from x(t):
h(t)=x(t)-m1(t) (2)
Normally, the first h(t) is not the IMF component of x(t). Treat h(t) as original signal and repeat the above steps. h(t) is treated as an IMF component when it satisfies the following conditions: 1) the number of extrema and the number of zero crossings must either equal or be different at most by one; 2) the mean value of the upper and lower envelopes of the signal is nearly zero.
A stopping criterion is given to determine whether h(t) is a IMF component or not, where the standard deviation (SD) of two consecutive results can be used as
 (3)
(3)
The value of SD is generally in the range of 0.2-0.3 [26,27]. When the value falls into this range, h(t) can be used as the first IMF component c1(t) of x(t). The rest component r1(t)=x(t)-c1(t) is taken as the original signal to carry out the next calculation until rn(t) falls into the range of SD or rn(t) becomes a monotonic function from which no IMF components can be extracted further. In this way, the original signal can be expressed as
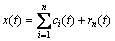 (4)
(4)
where ci(t) is the ith IMF component of x(t) and rn(t) is the nth residual error.
Apply Hilbert transformation on each IMF component as
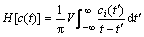 (5)
(5)
where V is Cauchy’s principle value.
Then, the original signal can be represented as
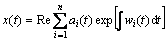 (6)
(6)
where Re means the real part, ai(t) is the amplitude function. ωi(t) is frequency function.
2.2 EMD method
The envelope curves of IMF components are analyzed after Hilbert transform. The amplitude function is expressed as
 (7)
(7)
The blasting vibration signal is a typical non-station random signal, which contains interference signal such as noise component [23]. The main IMF components which can represent the basic features of the blasting signal are selected to apply Hilbert transformation. By extracting amplitude envelope curve of composite signal of the several main IMF components, the actual delay time signal of detonator detonating is obtained [20]. The EMD method for identifying delay time is actually a process of denoising, reconstruction, selection and amplification of the original blasting vibration signal. Thus, the EMD method has high identification accuracy for its obvious and recognizable wave crests. The main problem of EMD method is that the main IMF components of the signal must be selected carefully by comparative analysis of all the IMF components. In addition, relevant experience and certain judgment ability are required for the analysts.
2.3 Instantaneous energy method
Hilbert instantaneous energy E(t) can be defined as
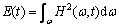 (8)
(8)
The initiation of each detonator in millisecond blasting is a procedure of energy mutation. The Hilbert instantaneous energy tells how the signal energy changes with time [21]. Therefore, the actual delay time can be identified by reading the energy mutation points which are generally the wave crests of the instantaneous energy curve. Compared with the EMD method, the instantaneous energy method interprets the complete original signal, not only several main IMF components.
3 Comparative study on delay time identification ability
3.1 Engineering survey
The comparative case study is a surge shaft of Songhuajiang River Water Conveyance Project in Jilin Province, China, which is set from the water supply tunnel to the surface. The height of the surge shaft is 50 m. The cross-section of the shaft is simple cylinder and the diameter is 20 m. The water supply tunnel has been excavated in advance and a mountain slope 10 m away from the surge is to be protected. The rock type of the surge shaft is mainly tuffaceous sandstone with great solidity. According to the Mohs scale, the hardness of the rock in the area is 10-12.
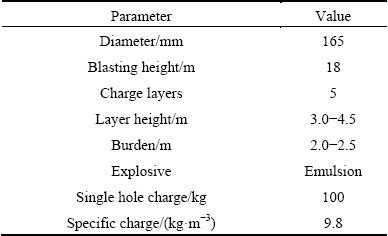
The surge shaft is excavated by deep-hole blasting. A guide shaft in the middle of the surge shaft is formatted primarily to provide free-face and compensation space for the main part blasting. The diameter of the guide shaft is 6 m. 50 holes of the guide shaft are arranged along four circles with different diameters, as shown in Fig. 1. Three blasting operations have been carried out and parameters for the first blasting are shown in Table 1.
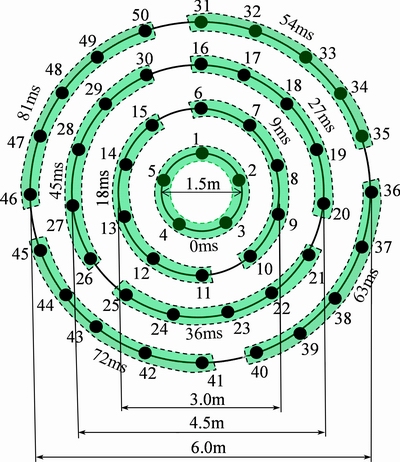
Fig. 1 Blasting holes arrangement and delay time
Table 1 Blasting parameters of surge shaft
As the deep blasting holes may skew for unavoidable construction factor, controlled blasting technique by using high-precision nonel detonators is required in the guide shaft blasting [29]. The combined initiation mode of detonators inside and outside the holes are used in the first blasting. The detonating delay time of neighboring segments in the same layer is 9 ms and for neighboring layers in the same hole it is 200 ms. Detonators of the both are installed outside the holes. The detonators with delay time of 1950 ms are uniformly installed inside the holes. Delay time of the first layer of explosives is shown in Fig. 1. During the blasting, five velocity stations were placed on the surface at different distances to monitor the ground vibration of three directions. The measuring results showed that the peak vertical particle vibration velocity was the largest among the three components of vibrations induced by blasting. So, the vertical particle velocities of the monitoring station are used in this work. The recorded signal of the vertical ground velocity in the third station is shown in Fig. 2.
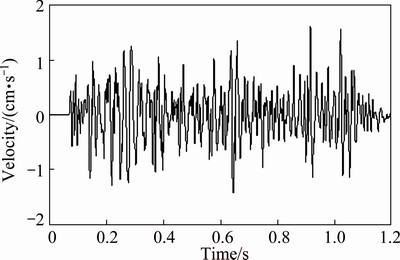
Fig. 2 Typical blasting signal of vertical vibration velocity
3.2 Comparative study of identification ability
Using the vertical velocity signal, twelve IMF components are obtained by empirical mode decomposition. Components of IMF 2, 3, and 4 are selected by comparative analysis of basic features of the original blasting signal and all the IMF components. According to Eq. (7), the envelope curve of composite signal with the three IMF components is obtained and given in Fig. 3. Obviously, each peak in the figure represents the detonators’ initiation of one segment.

Fig. 3 Envelope curve of IMF components by EMD identification method
Combining the envelope curve with the blasting design, delay time of each segment initiation can be clearly identified. Defining the first peak of the second layer of explosives as the first detonation, it can be seen from Fig. 3 that the identified delay time between two adjacent segments are 10.3, 7.6, 9.3, 9.4, 8.3, 9.7, 9.2, 10.2, and 9.6 ms. As the detonator’s error is ±1 ms, theoretical delay time range between two adjacent segmentations is 8-10 ms and most of identified delay time is in the error range. Some identified delay time beyond the error range may be caused by the simultaneous initiation of a segment with 5 holes.
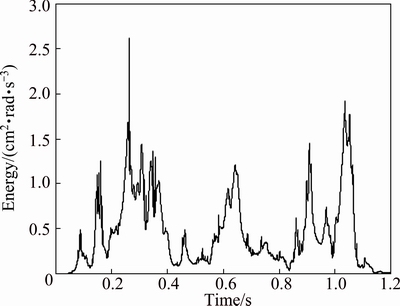
Fig. 4 Instantaneous energy curve of signal
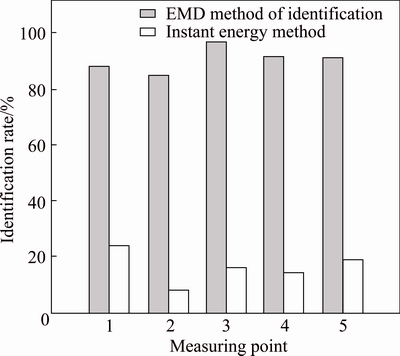
Fig. 5 Comparative identification rate of two methods
According to Eq. (8), the instantaneous energy curve of blasting signal is obtained and given in Fig. 4. Compared with the envelope curve of EMD identification method in Fig. 3, the distribution of instantaneous energy curve is more uneven and much less peak points can be identified to correspond to the blasting design times.
The recognition rates of the two methods at different monitoring stations are shown in Fig. 5. The recognition rates of EMD method are 88.2%, 84.6%, 96.8%, 91.6% and 90.9%, while those of instantaneous energy method are 24.6%, 8.2%, 15.8%, 14.2%, and 18.8%. It is evident that the recognition accuracy of instantaneous energy method for short millisecond blasting is extremely low, completely different from its high identification rate in long millisecond blasting (normally more than 25 ms) [21]. Conversely, the recognition accuracy of EMD method for short millisecond blasting is about 90%, close to long millisecond blasting. Thus, EMD method is more suitable for the delay time identification of short millisecond blasting than the instantaneous energy method.
3.3 Analysis of instantaneous energy method
To analyze the identification characteristics of the instantaneous energy method, single-hole blasting experiments with different charges were carried out. The instantaneous energy curves of single-hole blasting signals with 86 kg and 116 kg of explosives are given in Fig. 6. As shown, the instantaneous energy curve of single-hole blasting with different charges reaches the peak in different time. The larger the charge, the longer the peak-reaching and damping time. For blasting with 86 kg of explosives, the time from energy rising to damping is 32 ms, while for blasting with 112 kg of explosives, it is 52 ms. In order to make the peaks of instantaneous energy obvious and recognizable, the delay time of adjacent segments should be longer than half of the energy peak period [23]. For blasting with 86 kg and 112 kg of explosives, when the delay time is not less than 16 ms and 26 ms, respectively, it is feasible to identify the initiation time by instantaneous energy method. Otherwise, it is hardly to get high recognition accuracy.
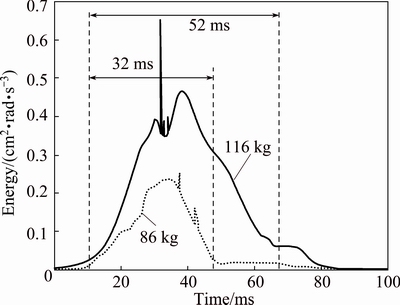
Fig. 6 Instantaneous energy curve of single-hole blasting
4 Optimization of blasting parameters based on EMD identification method
4.1 Engineering survey
Zijinshan Gold-copper Mine in Fujian Province is one of the largest scale open-pit mines in China. The mining area is located in the weathered rock above the diving surface. The rock type of the mine consists of medium grained granite, crypto-explosive breccia and porphyritic dacite. The rock is mainly hardness rock with some thin layer of weak rock locally.
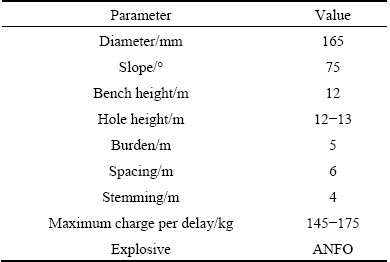
Deep-hole bench blasting is used in the mine. The bench height is 12 m and slope angle is 75°. The general applied design parameters are given in Table 2. The hole diameter of the bench blasting is 165 mm, and the burden, spacing and stemming lengths are 5 m, 6 m, and 4 m, respectively. Hole by hole blasting with high-precision nonel detonators (errors ±1 ms) is used in the mine. The detonating delay time between rows is 65 ms and the inter-hole initiation time is 25 ms. Detonators of the two are installed outside the holes. The detonators with delay time of 600 ms are uniformly installed inside the holes.
Table 2 General applied design parameters in Zijinshan mine
At present, the mine is facing two major problems as regards blasting: high large block ratio and the negative effect of blast-induced vibration on the final slope. According to the regulation that block with unilateral length longer than 600 mm is defined as large block, the large block ratio in the mine is usually as high as 8%, sometimes even more than 10%. The high large block rate leads to additional costs of secondary breaking, shoveling and loading. In addition, the final slopes have the characteristics of steep, great height, complexity rock properties and low stability [11]. Due to the influence of blast-induced vibration, small landslide of the final slopes has occurred several times in the mine. Therefore, the purpose of this work is to optimize blasting parameters by delay time identification, and thus to reduce the big block ratio and mitigate the vibration-effects.
4.2 Delay time identification and analysis based on EMD method
During the blasting, five velocity stations at different distances from the explosion source were installed on the platforms to monitor the three-directional ground vibration. The number of blasting holes at August 24th, 2015 was 45. The maximum charge of single hole and total charge were 175 kg and 7278 kg, respectively. The design delay time of each hole is given in Table 3. Also, the vertical particle velocities of the monitoring stations are used in this work. The recorded signal of the vertical ground velocity in the third station is shown in Fig. 7. The peak velocity of blasting vibration is 4.44 cm/s. It can be clearly seen from the figure that the vibration velocity in the second half is apparently higher than the first half.
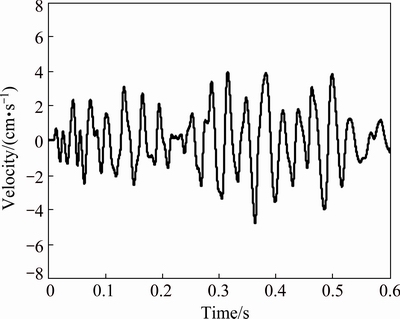
Fig. 7 Vertical vibration velocity under original blasting parameters
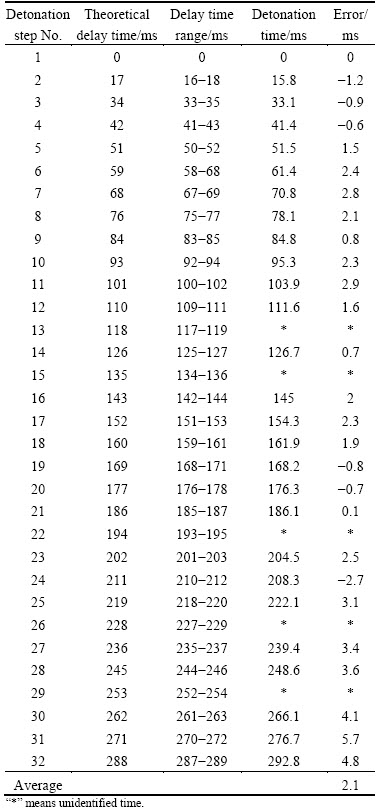
Using EMD method, the envelope curve of composite signal of the main IMF components is shown in Fig. 8. Defining the first peak as the time of the first detonation (0 ms), the subsequent detonation time obtained by EMD method is provided and compared with the design time in Table 3. The principle of matching the recognition time with design time is minimizing the errors between the two. The corresponding initiation sequences of identified time are displayed in Fig. 8. Only 25 of all 45 initiation time are successfully identified and the recognition rate is 55.6%. Because of the high recognition accuracy of EMD method in short millisecond blasting, the recognition rate reflects the real initiation of blasting at a certain extent. Low recognition rate shows that superposition effect of blasting vibration induced by delay error of detonators has appeared in the millisecond blasting under original parameters. For the first 20 initiation segments, the number of unidentified time is 5, while for the subsequent 25 segments it is 15. It is evident that the identification rate decreases with the increase of initiation segments. As the initiation errors of detonators could be accumulated gradually, the possible initiation time range of detonators after 20 segments is more than 10 ms (Table 3). Overlap of initiation time ranges is common between adjacent segments. The initiation time range for the 43rd segment is 414-450 ms, for instance, while for the 44th segment, it is 436-467 ms. So, overlapped initiation time range is 16 ms, which greatly increases the probability of simultaneous initiation or even sequentially reversed initiation. In addition, the disorder of initiation time could lead to increase of blasting vibration velocity, which can be verified by the difference of vibration velocity between the first and second half of the signal (Fig. 7). In view of this, it can be concluded that the demand of blast-induced vibration mitigation cannot be satisfied under original initiation precision of detonators. Thus, detonators with higher precision should be adopted to reduce the vibration effect in Zijinshan Gold-copper Mine.

Fig. 8 Delay time identification under original blasting parameters
Table 3 Comparison of design time and identified time under original blasting parameters

4.3 Delay time optimization based on EMD identify- cation method
Delay time of millisecond blasting has a great influence on rock fragmentation. The interference and superposition of stress wave could be increased by appropriately reducing of delay time [30]. To improve the rock breaking effect and mitigate the vibration effect, millisecond blasting with electronic detonators has been tested in Zijinshan Gold-copper Mine. The number of blasting holes at October 28th, 2015 was 32, and the maximum charge of single hole and total charge were 175 kg and 5124 kg, respectively. The detonating delay time between rows is 42 ms and the inter-hole initiation time is 17 ms. All the detonators are detonated by electronic detonators. The error of electronic detonator is ±1 ms, the same as high-precision nonel detonator. However, as the detonating time of each electronic detonator can be set separately, the initiation errors would not be accumulated gradually. The design delay time and delay time ranges are given and compared in Table 4. The vertical ground velocity signal under electronic detonators recorded by the third station is shown in Fig. 9. The peak velocity of ground vibration is 2.67 cm/s and the distribution of the velocity signal is more uniform than signal under high-precision nonel detonators (Fig. 7).

Fig. 9 Vertical vibration velocity under optimized blasting parameters
By using EMD method, the envelope curve and corresponding initiation sequences of identified time are shown in Fig. 10. The identified time, design time and errors between them are compared in Table 4. 27 of all 32 initiation time are successfully identified and the recognition rate is 84.4%. For the first 16 initiation segments, the number of unidentified time is 2, while for the rest, the number is 3. Apparently, there is no obvious difference of the identification rate with the increase of initiation segments. Furthermore, the average error under optimized parameters is 2.1 ms, less than original parameters (4.0 ms).
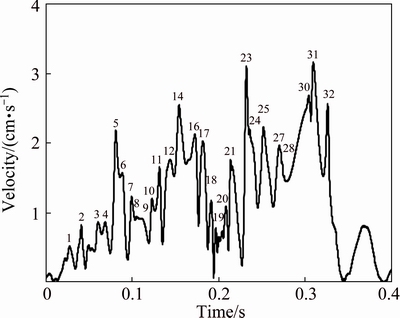
Fig. 10 Delay time identification under optimized blasting parameters
Delay time of blasting vibration signals recorded by other stations is also identified using EMD method and the identification rates with different types of detonators are compared in Fig. 11. The recognition rates with high-precision nonel detonators are 67.2%, 64.2%, 55.5%, 58.2%, and 51.1%, while those with electronic detonators are 92.3%, 89.4%, 84.4%, 82.1%, and 85.5%. Thus, electronic detonators detonating greatly decreases the probability of simultaneous initiation and sequentially reversed initiation, and the velocity peak of blasting vibration is reduced by more than 30% under almost the same maximum charge per delay.
Table 4 Comparison of design time and identified time under optimized blasting parameters
4.4 Blasting optimization to reduce large block ratio
The large block ratio has been reduced from more than 8% to about 6% by blasting optimization of delay time and detonating detonators. However, rock fragmentation is influenced by numerous factors, such as specific charge, charge structure, burden, and spacing [31]. Therefore, further optimization is needed to reduce costs of secondary breaking, shoveling and loading. Through the field investigation, it is found that large blocks are mainly concentrated in the first row of holes. There are fractures caused by previous blasting on the slope and the front bench close to the first row of holes. During blasting, explosive stress wave and explosive gas act directly on the fractures and the large blocks are pushed out before fully broken. Furthermore, because of unavoidable construction factors, such as hole deviation, over and under excavation, the burdens of the first row of holes are usually uneven.
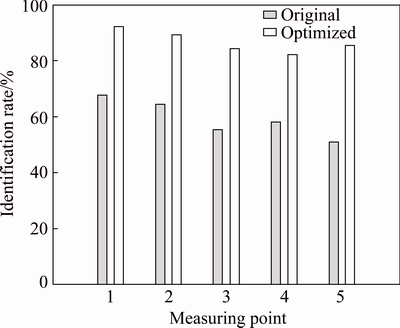
Fig. 11 Comparison of identification rates under different parameters
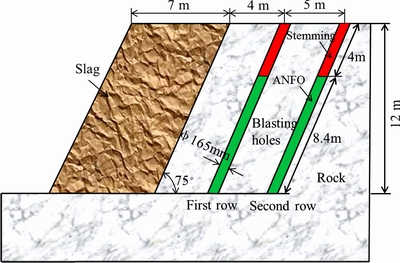
Fig. 12 Blasting optimization scheme to reduce large block ratio

Fig. 13 Comparative photos rock fragmentation
To effectively reduce the large block ratio, two aspects of the original blasting scheme are optimized. Firstly, slag-remaining blasting is used to increase the acting time of explosive stress wave and explosive gas. After each blasting, the blocks are not completely shoveled with 7 m in thickness of slag remaining (Fig. 12). Secondly, the burden of the first row of holes is reduced from 5 m to 4 m, while other rows remain 5 m. Photos before and after optimization are shown in Fig. 13. The statistical data shows that the large block ratio is successfully reduced to no more than 3%, and responsively, the average shoveling efficiency increases from 320 t/h to 490 t/h. The results illustrate that reducing the large block ratio by slag-remaining blasting and burden optimization of the first row in Zijinshan Gold-copper Mine is effective.
5 Conclusions
1) The capabilities of empirical mode decomposition (EMD) method and instantaneous energy method based on Hilbert-Huang transform (HHT) in identifying the initiation times during short millisecond blasting were comparatively studied through a case study of surge shaft blasting project. It is found that the recognition accuracy of EMD method of short millisecond blasting is close to long millisecond blasting. While the recognition accuracy of instantaneous energy method of short millisecond blasting is much lower than long millisecond blasting. To get a high recognition accuracy by instantaneous energy method, the delay time of adjacent segments should be longer than half of the energy peak period.
2) The EMD method is used to identify the delay time of millisecond blasting in Zijinshan Gold-copper Mine. The identification results show that the initiation errors accumulated gradually lead to increasing of blasting vibration velocity. By optimizing the design of delay time and detonating detonators, the velocity peak of blasting vibration is reduced by more than 30% under almost the same maximum charge per delay. Moreover, slag-remaining blasting and burden optimization of the first row are effective ways to reduce the large block ratio.
3) HHT is of great significance to analyze the characteristics of blasting vibration signals. The identification technologies based on HHT are helpful to optimize the blasting parameters and improve the blasting process. In addition, studies in these regards are ongoing, and further researches may lead to higher recognition accuracy.
Acknowledgments
The authors are grateful to the School of Resources and Safety Engineering of Center South University and Zijin Mining Group Co. Ltd for their supports. The authors are also very grateful to the staff of Zijinshan Gold-copper Mine for their hospitality and invaluable support during the field investigation.
References
[1] NATEGHI R. Evaluation of blast induced ground vibration for minimizing negative effects on surrounding structures [J]. Soil Dynamics and Earthquake Engineering, 2012, 43: 133-138.
[2] KUZU C, GUCLU E. The problem of human response to blast induced vibrations in tunnel construction and mitigation of vibration effects using cautious blasting in half-face blasting rounds [J]. Tunnelling and Underground Space Technology, 2009, 24(1): 53-61.
[3] AK H, IPHAR M, YAVUZ M, KONUK A. Evaluation of ground vibration effect of blasting operations in a magnesite mine [J]. Soil Dynamics and Earthquake Engineering, 2009, 29(4): 669-676.
[4] LU C P, DOU L M, WU X R, XIE Y S. Case study of blast-induced shock wave propagation in coal and rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(6): 1046-1054.
[5] MONJEZI M, GHAFURIKALAJAHI M, BAHRAMI A. Prediction of blast-induced ground vibration using artificial neural networks [J]. Tunnelling and Underground Space Technology, 2011, 26(1): 46-50.
[6] WANG Zhen-yu, LIANG Xu, CHEN Yin-lu, LI Fu-qian, LIU Guo-hua. Study of safety evaluation method of blasting vibration based on input energy [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(12): 2492-2499.
[7] SHI Xiu-zhi, CHEN Shou-ru. Explosive blasted per delay and burden effects on the time-frequency characteristic of vibration induced by blast [J]. Journal of China Coal Society, 2009, 34(3): 345-349.
[8] WU C S, LI J X, CHEN X, XU Z P. Blasting in twin tunnels with small spacing and its vibration control [J]. Tunnelling and Underground Space Technology, 2004, 19: 518.
[9] ALDAS G G U, ECEVITOGLU B. Waveform analysis in mitigation of blast-induced vibrations [J]. Journal of Applied Geophysics, 2008, 66(1): 25-30.
[10] SONG Guang-ming, ZENG Xin-yu, CHEN Shou-ru, WU Cong-shi. The selection of millisecond delay interval of blasting for decreasing ground vibration based on the wavelet packets prediction model of waveforms [J]. Explosion and Shock Waves, 2003, 23(2): 163-168.
[11] SHI X Z, CHEN S R. Delay time optimization in blasting operations for mitigating the vibration-effects on final pit wall’s stability [J]. Soil Dynamics and Earthquake Engineering, 2011, 31(8): 1154-1158.
[12] WU T F, WANG K. Summary of current studies on millisecond blasting technique [J]. Blasting, 1997, 14(1): 53-57.
[13] CHEN Shi-hai, YAN Yong-feng, QI Gui-feng, ZHANG Xian-kun, ZHANG Wei. Analysis of influence factors of interference vibration reduction of millisecond blasting [J]. Rock and Soil Mechanics, 2011, 32(10): 3003-3008.
[14] ZHAO Ming-sheng, LIANG Kai-shui, YU De-yun, REN Shao-feng. Effect of segments on time-frequency characteristics of blasting vibration signal [J]. Journal of China Coal Society, 2012, 37(1): 55-61. (in Chinese)
[15] ZHAO Ming-sheng, ZHANG Jian-hua, YI Chang-ping. Time- frequency analysis based on single-stage addition of wave-forms of blasting vibration signals [J]. Journal of China Coal Society, 2010, 35(8): 1279-1282.
[16] LING T H, LI X B. Time-energy analysis based on wavelet transform for identifying real delay time in millisecond blasting [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(12): 2266-2270.
[17] XU Hong-tao, LU Wen-bo, CHEN Ming, LI Rui-qing. Study on superposition effect of blasting vibration induced by delay error of detonators using genetic algorithm [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 29(7): 1900-1904.
[18] ZHANG Sheng, LING Tong-hua, LIU Hao-ran, CAO Feng. Pattern adapted wavelet time-energy density method and its application in millisecond blast vibration signal analysis [J]. Journal of China Coal Society, 2014, 39(10): 2007-2013.
[19] QIAN Shou-yi, LI Qi-yue. HHT instantaneous energy method to identify of delay time in millisecond blasting [J]. Mining Research and Development, 2012, 32(2): 113-116.
[20] ZHANG Yi-ping, LI Xi-bing, ZHAO Guo-yan. The method of using EMD to identify time of delay in millisecond blasting [J]. Chinese Journal of Underground Space and Engineering, 2006, 2(3): 488-490.
[21] WANG Zhen-yu, FANG Cheng, CHEN Yin-lu, CHENG Wei-feng. A comparative study of delay time identification by vibration energy analysis in millisecond blasting [J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 60: 389-40.
[22] GONG Min, QIU Yi-ke-ke, LI Yong-qiang, MENG Xiang-dong. Application of measuring and identifying detonation time of customized detonator in blasting design of urban tunnels [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(6): 1179-1187.
[23] GONG Min, QIU Yi-ke-ke, MENG Xiang-dong, LI Yong-qiang, ZENG Gong-jian, TANG Sheng. Identification method of detonator’s actual firing time delay based on HHT and its application in millisecond blasting under urban environment [J]. Journal of vibration and shock, 2015, 34(10): 206-212.
[24] MA Xiao-ming, WANG Zhen-yu, CHEN Yin-lu, LIANG Xu, CHENG Wei-feng. Analysis of energy distribution of accurate millisecond blasting vibration [J]. Journal of PLA University of Science and Technology: Natural Science Edition, 2012, 13(4): 449-454.
[25] XU Zheng-yang, YANG Jun, CHEN Zhan-yang. Precise time frequency analysis on seismic signal by hole initiation using high precision detonators [J]. Journal of China Coal Society, 2013, 38(S2): s331-s336.
[26] HUANG N E, SHEN Z, LONG S R, WU M C, SHIN H H, ZHENG Q, YEN N C, TUNG C C, LIU H H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society A: Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903-995.
[27] HUANG N E, SHEN Z, LONG S R. A new view of nonlinear water waves: The Hilbert spectrum [J]. Annual Review of Fluid Mechanics, 1999, 31: 417-457.
[28] PENG Z K, TSE W P, CHU F L. A comparison study of improved Hilbert Huang transform and wavelet transform: Application to fault diagnosis for toiling bearing [J]. Mechanical System and Signal Processing, 2005, 19: 974-988.
[29] SHI Xiu-zhi, QIU Xian-yang, ZHOU Jian, WANG Yang, NIE Jun, LI Bi-hong. Technology and case study of ultra-large section and high shaft excavation by short-millisecond spherical-like blasting [J]. Chinese Journal of Rock Mechanics and Engineering, 2016.
[30] DANIEL J, FINN O. Shock wave interactions in rock blasting: The use of short delays to improve fragmentation in model-scale [J]. Rock Mechanics & Rock Engineering, 2013, 46(1): 1-18.
[31] FARAMARZI F, MANSOURI H, FARSANGI MAE. A rock engineering systems based model to predict rock fragmentation by blasting [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60(8): 82-94.
基于HHT的延期时间识别法在精确短延时爆破优化中的应用
史秀志,邱贤阳,周 健,陈 新,范玉乾,卢二伟
中南大学 资源与安全工程学院,长沙 410083
摘 要:延时爆破中延期时间的准确识别对于优化爆破设计和降低爆破振动效应具有重要作用。以超大断面调压竖井导井爆破为例,对比分析了基于Hilbert-Huang 变换(HHT)的EMD识别法和瞬时能量识别法在精确短延时爆破中的延期时间识别能力,发现EMD识别法的识别率在80%以上,而瞬时能量法识别率低于25%。通过单孔爆破振动信号瞬时能量分析表明,瞬时能量识别法适用于延期时间大于瞬时能量峰值半周期的微差爆破。将EMD识别法应用于紫金山露天矿微差爆破延期时间识别,为降低爆破振动和爆破大块率,以识别结果为依据对爆破参数进行了优化。现场实测数据表明:通过优化起爆雷管和延期时间,相同单孔药量下爆破振动降低30%以上;结合压渣爆破和前排抵抗线优化,爆破块度成功降低到3%以下。研究结果证明了基于HHT的延期时间识别法能有效实现爆破设计的优化,该识别方法对于其他类似爆破工程的设计优化具有一定的参考价值。
关键词:延期时间识别;短延时爆破;精确起爆;爆破降振;Hilbert-Huang 变换(HHT)
(Edited by Yun-bin HE)
Foundation item: Project (2013BAB02B05) supported by the National 12th Five-Year Science and Technology Supporting Plan of China; Project (2015CX005) supported by the Innovation Driven Plan of Central South University of China; Project (2016zzts094) supported by the Fundamental Research Funds for the Central Universities of Central South University, China
Corresponding author: Xian-yang QIU; Tel: +86-13467598816; E-mail: qiuxianyang_csu@163.com
DOI: 10.1016/S1003-6326(16)64310-8
Abstract: The accurate identification of delay time in millisecond blasting plays an important role in the optimization of blasting design and reduction of vibration effect. Through a case study of a surge shaft blasting project, the capability of the EMD (empirical mode decomposition) method in identifying the delay time of short millisecond blasting with precise initiation was compared with the instantaneous energy method based on Hilbert-Huang transform (HHT). The recognition rate of the EMD method was more than 80%, while the instantaneous energy method was less than 25%. By analyzing the instantaneous energy of single-hole blasting signal, it was found that the instantaneous energy method was adaptable to millisecond blasting with delay time longer than half of the energy peak period. The EMD method was used to identify delay time of millisecond blasting in Zijinshan open-pit mine. According to the identification results, the blasting parameters were optimized for controlling the blast-induced vibration and reducing the large block ratio. The field data showed that the velocity peak of ground vibration was reduced by more than 30% under almost the same maximum charge per delay by the optimization of delay time and detonating detonators. Combining with slag-remaining blasting and burden optimization of the first row, the large block ratio was reduced to less than 3%. The research results proved that the identification method based on HHT was feasible to optimize the blasting design. The identification method is also of certain reference value for design optimization of other similar blasting projects.


