J. Cent. South Univ. Technol. (2007)01-0129-06
DOI: 10.1007/s11771-007-0026-z
Effective stress analysis method of seismic response for high tailings dam
LIU Hou-xiang(柳厚祥)1, 2, LI Ning(李 宁) 2, LIAO Xue(廖 雪)3, WU Cong-shi(吴从师) 1, PAN Xu-dong(潘旭东) 1
(1. Institute of Geotechnical Engineering, Changsha University of Science and Technology,Changsha 410076, China;
2. Institute of Geotechnical Engineering, Xi’an University of Technology, Xi’an 710048, China;
3. Communications Bureau of Hunan Province, Changsha 410011, China)
Abstract:
Based on the analysis method for tailings dam in upstream raising method presently used in metallurgy and nonferrous metals tailings depository in the world, an effective stress analysis method of seismic response for high tailings dam was developed according to the results of engineering geological exploration, static and dynamic test and stability analysis on Baizhishan tailing dam 113.5 m high. The law of generation, diffusion and dissipation of seismic pore water pressure during and after earthquake was investigated, and the results of tailings dam’s acceleration, seismic dynamic stress and pore water pressure were obtained. The results show that the seismic stability and liquefaction resistance of high tailings dam are strengthened remarkably, and the scope and depth of liquefaction area at the top of dam are reduced greatly. The interior stress is compressive stress, the stress level of every element is less than 1.0 and the safety coefficient of every element is greater than 1.0. The safety coefficient against liquefaction of every element of tailing dam is greater than 1.5 according to the effective stress analysis of seismic response by finite element method. The calculated results prove that liquefaction is the main reason of seismic failure of high tailing dams, and the effect of seismic inertia forces on high tailing dams’ stability during earthquake is secondary reason.
Key words:
1 Introduction
In terms of the upstream raising technology in metallurgy and nonferrous metals mine tailings depository in the world, the technique of filling a pool, setting scattertubes and accreting sub-dams by bulldozer with human labour is usually used[1-6]. With the advance of science and technology, engineers attempt to improve the structure of dams and their working conditions, enhance the stability of dams and reduce labor intensity. Dynamic stability and against liquefaction of high tailing dams in seismically active area are always important problems. LIU[7] proposed nonlinear seismic response analysis of high tailings or earth dam by finite element method(FEM), which can successfully settle the dynamic stability problem of tailings dam. But the law of generation, diffusion and dissipation of seismic pore water pressure during and after earthquake is also an important problem of numerous engineers and technicians pay attention to. Therefore, in this study, based on engineering geological prospecting, static and dynamic test on Baizhishan tailings dam of 113.5 m high of Daye Iron Mine of Wuhan Steel and Iron Company(in China), an effective stress analysis of seismic response of high tailing dam was carried out, and the results of tailings dam acceleration, seismic dynamic stress and pore water pressure were obtained.
2 Physical performance and static or seismic character tests of tailings
2.1 Law of tailings deposit and geological profile of tailings dam
After the distribution law of deposit and the structures of tailings dam are formed about 3-5 years, three representative profile lines were selected to do engineering geological exploration. The results show that the accreting dams consist of fine tailings sand, powder sand, powder soil and tailing powder clay (see Fig.1). Because of the hydraulic alluvial separation, the deposit law of coarse granule at the top, fine granule at the bottom, coarse in the front of dams shell and fine in the interior is found. In addition, tailing powder sand intersects tailing powder-soil and consolidation law (the density is successively a little , middle and entire dense from top to bottom dam) are also included. However, from the geological profile of tailings dam it is found that the sub-dams formed by cyclone separator are composed of fine tailings in the scope of side fields about 6-8 m. These sub-dams have the advantages of coarse soils, well-graded and high density soils, high strength and good seepage condition. So they can safeguard the dams very well.
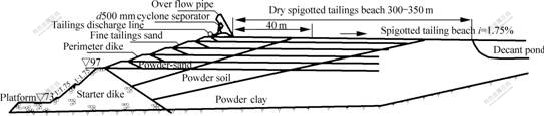
Fig.1 Geological profile of tailings dam
2.2 Physical performance of tailings
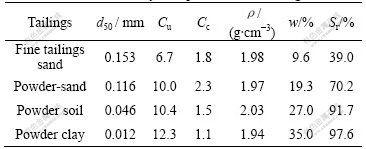
Tailings sample has four compositions: fine tailings sand, powder-sand, powder soil and powder clay. According to Ref.[8], relative volume mass, density, relative density and size gradation were respectively measured. The results are shown in Table 1, where d50 is the middle diameter, Cu is the coefficient of uniformity, Cc is the coefficient of curvature, ρ is bulk density, w is the mass fraction of water, Sr is the saturation degree.
Table 1 Physical parameters of tailings
2.3 Static characters of tailings
The determination of the static character of tailings is made up of compressive test, permeability test, direct shear test and triaxial shear test. In drained triaxial shear test, the all-round pressure (σ3) is 100, 200, 300 and 400 kPa, respectively. Table 2 lists Duncan nonlinear
parameters and some parameters of tailings, where ρm is the saturated density; C′ is the cohesion intercept; φ′ is the angle of shearing resistance; K, n, Km, m, Rf, k are the modulus coefficient, modulus exponent, volumetric modulus coefficient, volumetric modulus exponent, breaking ratio and permeability coefficient, respectively[9].
2.4 Seismic characters of tailings
2.4.1 Vibration triaxial shear test
In seismic test, the DCJ-78 electromagnetism vibration triaxial shear device was used. After the saturated sample was put into a pressure chamber at different consolidation ratios and different lateral pressures, it began to be consolidated. Different steady axial fierce vibration forces with sine waveform were exerted when consolidation was steady. The seismic stress σd, axial strain ε d and pore-water pressure u were determined. The kinetic triaxial liquefaction test was carried out at three consolidation ratios (kc =1.0, 1.5, 2.0) and three lateral consolidation pressures (σ3=100, 200, 300 kPa), therefore kinetic stress, kinetic strain, liquefaction shear stress and liquefaction cycle were determined with seismic parameters C1, C2, C3 and C4, C5[10]. The results are listed in Table 3, where Eur is the bulk modulus of resilience, νd is the seismic Poisson ratio, λmax is the maximum damping ratio.
2.4.2 Common vibration column test
The common vibration column test provides the deformation characteristic parameters, such as the maximal seismic shear modulus Gmax, the average effective stress σ′m and damping ratio λ and the relation between seismic shear modulus G, damping ratio λ and seismic shear strain γd. Usually, the seismic shear modulus and damping ratio λ in the scope of 1×10-4- 1×10-3 can be determined by seismic triaxial shear test. But in the case of earthquake, the change scope of λ for sand-soil is from 1×10-5 to 1×10-3. So a DTC-158 common vibration column triaxial shear device made in Japan was used. At enclosing pressure σ3 of 100, 200, 400, 600 kPa, respectively, the tests were performed to determine seismic strain parameters k1 and k2[10]. The results are also shown in Table 3.
Table 2 Static parameters of tailings
Table 3 Seismic parameters of tailings
3 Calculative model of analysis of seismic response for tailings dam
3.1 Main parameters of calculation
According to Ref.[6], the tailings pond considered is the second grade. In terms of “Design Specification of Structures anti-seismic”, for tailings dam which exceeds the second grade, the analysis method of two- dimensional time-procedure response should be adopted to analyze the anti-seismic which includes seismic liquefaction and stability. Supposing each kind of tailings is visco-elasticity, the nonlinear FEM was applied to analyze the seismic response for tailings dam. From the results of tests and engineering geological exploration and consulting relative means to do synthetic analysis, some seismic characteristic parameters applied are shown in Table 3.
3.2 Selection of earthquake wave
In the light of anti-seismic structure in Wuhan District, the stability against liquefaction in Baizhishan tailings dam should be checked when earthquake intensity is 7?. Because the future wave of earthquake cannot be predicted correctly now, some reasonable hypotheses should be made. So, suppose the foundation only has stiffness without mass and put the ground seismic vibration on the boundary of calculation zone meanly. The post earthquake accelerogram recorded at Tangshan earthquake was chosen[7] (see Fig.2) and its remarkable cycle was adjusted from 0.14 s to 0.30 s, the maximal acceleration to 0.98 m/s2 and seismic duration to 10 s.
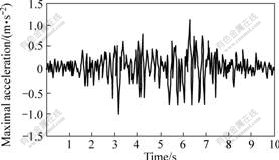
Fig.2 Post earthquake accelerograms recorded at Tangshan earthquake
4 Seismic response analysis of undrained effective stress
4.1 Model and principal calculative parameters
Based on engineering geological prospecting of tailings dam in upstream raising method, a calculative model was set up (Fig.1). In analysis of finite element method, considering the engineering geological conditions, the calculation zone includes a part of natural foundations, the calculation border is medium weathered irruptive rock and the border conditions are 30 fixed points at bottom and 16 points on two sides. They are all fixed on horizontal in static analysis and on vertical in dynamic analysis, respectively. The same elements are adopted in the course of static and dynamic FEM analysis[11-12]. The principal calculative parameters applied are shown in Table 3.
4.2 Dynamic equation and directly integrate method
The dynamic equation of tailings dam is
(1)
where [G], {
}, {
}, {u} are respectively the transformation matrice which are from three volumes of seismic acceleration to n-dimensional space, the column matrix of acceleration, the column matrix of velocity and the column matrix of displacement, [M] is the mass matrix attained by the method of concentration mass under which mass of element is focused on the nodes, [K] is stiffness matrix, and [C] is the damping matrix attained by theory of Rayleigh damping, [C]= α[M]+ β [K][13-16].
For the non-uniformity of tailings material element, the damping matrix is worked out and then added.
(2)
where 
, λ and ω1 are the damping ratio and main vibration frequency, respectively.
Eqn.(1) is a group of nonlinear equations which can be solved using method of Wilson-θ to directly integrate. It is supposed that the change of acceleration is linear during the time of θΔt. When original conditions 
and 
being known and applying θ equal to 1.4 in order to ensure stability at any cases, velocity 
, acceleration
, dynamic strain
and dynamic stress 
of element can be obtained after getting displacement {u} at the moment. This kind of calculation is done one by one according to the period, up to the end of earthquake. Considering the nonlinear relation between kinetic stress and kinetic strain, the iteration method is adopted so as to adapt dynamic shear modulus G and damping ratio to average dynamic shear strain γd. In iteration, Gi-1 at first adopted is substituted into dynamic equation to get average kinetic shear strain γd. Then γd is substituted to get new shear modulus. That the ratio (Gi-1-Gi )/Gi is less than 0.1 is the standard of iteration convergence. Usually, after twice or three times it can converge and the convergence precision is higher.
According to the shear stress diagram and Seed’s method, equivalent cycles (Neq=5) corresponding to the average shear stress τav=0.65(τxy)max at the circumstance, liquefaction standard is used to check the average (effective) shear stress τav caused by earthquake against liquefaction shear stress τl in triaxial shear test[11]. When the average shear stress is greater than the liquefaction shear stress (τav＞τl), the element can be liquefied. On the contrary, the element cannot be liquefied. Safety coefficient of anti-liquefaction of each element (Fs)l is
(Fs)l=τl/τav (3)
where τl and τav are respectively even shear stress causing liquefaction and average shear stress in five cycles. τl can be obtained based on initial shear stress each unit and triaxial shear test.
4.3 Seismic response analysis of undrained effective stress
The material of tailings is a kind of discrete aggregate with much void which can seepage and drain. So the drainage circumstance should be considered in the analysis of seismic response. It is supposed that void is not sealed in the skeleton of tailings mineral during the short seismic duration. During the earthquake, pore-water pressure grows gradually, effective stress continues to drop, and dynamic shear modulus not only shows linear change with the increase of shear strain, but also reveals an decrease with the increase of effective stress. And the influence between the diffusion and dissipation of seismic pore water pressure is overlooked in the analysis. The seismic process is divided into 10 phases, in which they are iterated so that G and D of this period suit average shear strain γd. Then the increment of the pore-water pressure of each element can be calculated as follows[13]:
Δpg=EurΔεv (4)
The effective stress at the end of one phase can be used to modify G, which is used for the first iteration at next phase. Static analysis is performed at the end of each phase. The effective stress calculated could be used to judge liquefaction, which will happen when the effective stress is equal to zero or smaller. The distribution of pore water pressure in dam is shown Fig.3.
Fig.3 Distribution of pore-water pressure in dam (unit: kPa)
5 Nonlinear seismic response analysis of drained-effective stress
A fine tailings sand shell with higher strength and better seepage condition is added on the outer slope of tailings dam. Considering its influence, it is more suitable to analyze the nonlinear seismic response of drained-effective stress. When the method is used, not only the gradual generation of seismic pore-water pressure, but also the process of diffusion and dissipation of seismic pore-water pressure are taken into. During the seism, because of generation of the seismic pore-water pressure, stress of any place in tailings dam should meet the following equilibrium and unstable seepage equations:
(5)
(6)
(7)
where εx and εy are respectively normal strains in directions x and y, kx and ky respectively permeability coefficient in direction x and y.
Calculation is also carried out in each phases divided, and Biot consolidation theory is put into use to evaluate the influence of diffusion and dissipation of seismic pore-water pressure. Flow diagram of effective stress analysis of seismic response is shown in Fig.4.
For this tailings dam, if earthquake intensity is 7?, acceleration response diagrams at nodes 390 and 399 are
shown in Fig.5. The distribution of dynamic shear stress response in high tailings dam is shown in Fig.6. The distribution of pore-water pressure in high tailings dam is shown in Fig.7 and isogram of safety coefficient against liquefaction in dam is shown in Fig.8.
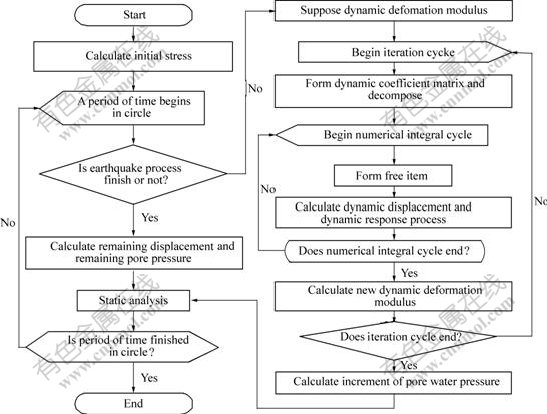
Fig.4 Flow diagram of effective stress analysis of seismic response
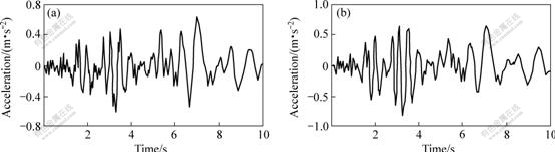
Fig.5 Acceleration response diagrams at nodes 390(a) and 399(b)
Fig.6 Distribution of dynamic shear stress τav in high tailings dam (Unit: kPa)
Fig.7 Distribution of pore-water pressure in high tailings dam (Unit: kPa)
Fig.8 Isograms of safety coefficient against liquefaction in high tailings dam
6 Conclusions
1) The deposit law of tailings dam in upstream raising method of coarse granule at the top, fine granule at the bottom, coarse in the front of dams shell and fine in the interior is found. Three representative profile lines are selected to do engineering geological exploration. The accreting dams consist of fine tailing sand, powder sand, powder soil and tailing powder clay.
2) The law of generation, diffusion and dissipation of seismic pore-water pressure during and after earthquake is attained, the isograms of safety coefficient against liquefaction and the results of tailings dam acceleration, seismic dynamic stress and pore-water pressure are obtained. The scope and depth of liquefaction area at the top of dam are reduced greatly. The safety coefficient against liquefaction of every element of high tailings dam is greater than 1.5 according to the effective stress analysis method. The safety coefficient against liquefaction of most part elements is improved, except that a small scope in shallow layer of slope surface on the top in tailings dam may liquefy.
3) Liquefaction is the main reason of seismic failure of high dams , and the effect of seismic inertia forces on high dams’ stability during earthquake is secondary.
References
[1] LIU Hou-xiang, LI Ning, LIAO Xue, et al. A new technique of combining accretion by cyclone separator and scattertube for tailings dams[J]. Journal of Central South University of Technology, 2004, 11(2): 185-191 .
[2] DOBRY R, ALVARZE L. Seismic failure of Chilean tailings dams[J]. Journal of Soil Mechanics and Foundation, 1967, 93(5): 83-108.
[3] ZHOU Liu-xia. Accidents of some tailings dams abroad: causes and lessons[J]. Journal of Mining and Metallurgical Engineering, 1990, 10(2): 64-66.(in Chinese)
[4] Tailing Dam Safety Investigation Group of Ministry of Metallurgy. Investigation report about safety stability of tailings dams in China[R]. Beijing: Ministry of Metallurgy, 1987.(in Chinese)
[5] STEVEN G V. Planning, Design and Analysis of Tailings Dams[M]. New York: Wiley-Interscience Publication, 1983.
[6] MO Lu-shen, WANG Zhi-ping, CHEN Sou-ren, et al. ZBJ1-90 design specification of the tailings[S]. Beijing: China Plan Press, 1991.(in Chinese)
[7] LIU Hou-xiang. A Study of the Nonlinear Seismic Response Analysis of High Tailings or Earth Dams by FEM [D]. Changsha: Changsha Research Institute of Mining and Metallurgy, 1993. (in Chinese)
[8] SHENG Shu-pan. SL237-1999 specification of soil test[S]. Beijing: China Hydraulic Press, 1999.(in Chinese)
[9] CIVIDINI A, GIODA G. Finite-element approach to the erosion and transport of fine particles in granular soils[J]. International Journal of Geomechanics, ASCE, 2004, 4(3): 191-198.
[10] MEJIA L H, SEED H B. Comparison of 2D and 3D dynamic analyses of earth dams[J]. Journal of the Geotechnical Engineering, ASCE, 1983, 109(11): 1383-1398.
[11] HONG Yu-kang. Foundation Soil Science and Soil Mechanics[M]. Beijing: The People’s Communication Press, 2000.(in Chinese)
[12] WEN Si-ping, QIU Jia-kui, LIU Hou-xiang. Optimization of the new process for highly-constructing of subdam and comprehensive measures for flood prevention of Xishimen Iron Mine’s tailings pond[J]. Journal of Mining and Metallurgical Engineering, 1997, 17(3): 1-5. (in Chinese)
[13] ZHOU J, XU Z Y. 3-D dynamic effective stress analysis of earth/tailings dams[C]// Int Symposium on Environmental Geotechnology. Berkeley: California University Press, 1986.
[14] WU Ai-xiang, SUN Ye-zhi, LI Qing-song. Self-organized criticality of liquefaction in saturated granules[J]. Trans Nonferrous Met Soc China, 2003, 13(1): 180-183.
[15] BROMHEAD E N. The Stability of Slopes[M]. New York: Surrey University Press, 1986.
[16] WU Ai-xiang, GU De-sheng, SUN Ye-zhi, et al. Experiment and mechanism of vibration liquefaction and compacting of saturated bulk solid[J]. Journal of Central South University of Technology, 2001, 8(1): 34-39.
(Edited by CHEN Wei-ping)
Foundation item: Projects(03JJY3078, 04JJ40032) supported by the Natural Science Foundation of Hunan Province, China; project(03A006) supported by Scientific Research Fund of Hunan Provincial Education Department, China
Received date: 2006-05-25; Accepted date: 2006-07-27
Corresponding author: LIU Hou-xiang, Professor; Tel:+86-731-5040229; E-mail: liuhoux1@163.com
