J. Cent. South Univ. Technol. (2008) 15(s1): 215-220

DOI: 10.1007/s11771-008-349-4

Application research on metal rheological forming of reproducing kernel partial method

YIN Shui-ping(殷水平), LUO Ying-she(罗迎社), YU Min(余 敏)

(Institute of Rheological Mechanics and Material Engineering,

Central South University of Forestry and Technology, Changsha 410004, China)

Key words:

numerical simulation; meshless method; reproducing kernel partial method(RKPM); rheological forming；

1 Introduction

Numerical methods, such as finite element method and boundary element, have been greatly succeeded in engineering. However, the generation and existence of grid caused some difficulties in their applications^[1]. For example, there are a large number of large elastic-plastic deformation problems in the engineering such as plastic forming, structural impact and so on. It is usually to use remeshing technology to get more accurate results when simulating it with FEM and the accuracy would be greatly reduced^[2-3]. So far, the developed meshless methods can completely or partly eliminate the grid and have broad application in simulating crack growth, elastic-plastic analysis, large deformation, impact and so on. It is not only the current research focal point in scientific and numerical method in engineering, but also the trend in future^[4-5].

Compared smoothed particle hydrodynamic method (SPH) with element-free method (EFG), the latter has its advantage of compatibility, stability, high precision and strong applicability^[6-7]. However, EFG costs more than SPH. Reproducing kernel partial method (RKPM) not only completely eliminates the instability of SPH, but also has the advantage that the other meshless element-free methods do not have^[8]. In this work, the RKPM is used to solve the rigid-plastic problem.

Levy-Misses equation and Misses yielding criteria were used to solve the displacement and velocity of node by rigid-plastic meshless method, which was used to solve the geometric non-linear problems related in dispersing space by velocity integrating. Thus, it is a relatively simple and efficient solution. Its accuracy can meet the engineering requirements. Rigid-plastic meshless method cannot analyze unloading or obtain remanent stress, deformation and rebound because of ignoring elastic deformation. Rigid-plastic meshless method is based on the rigid-plastic material variational principle, the main treatment methods of boundary conditions are Lagrange multipliers, compressible volume of material and penalty functions^[9]. Compressible volume method is used in this work.

2 Meshless analysis of metal rheological forming problems

The basis of rigid-plastic meshless method is variational principle of rigid-plastic material. The variational principle considered that the allowance velocity is the true velocity field when the total energy consumption functional E(u) reaches the minimum value. That is to say, the variational principle changes the problem of plastic partial differential equations to be solved into the ultimate-value problems of functional in the form of energy integral, and establishes the basic equation of meshless method by the form of this conversion^[10]. The stress calculation of this method does not depend on superposition, but the constitutive relationship.

Rigid-plastic material should meet the following equations and boundary conditions in the plastic region^[11]:

1) Equilibrium differential equation

σ_{ij, j}=0                                      (1)

2) Misses yielding condition

                            (2)

3) Geometrical equation

                            (3)

4) Constitutive equation

                                (4)

5) Boundary conditions

                           (5)

                               (6)

where   is the equivalent strain; and there is

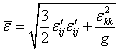                         (7)

The equivalent integral form of equilibrium equation and boundary conditions can be gotten from the method of weight residual, and the total energy dissipation during deformation can be expressed as

            (8)

                        (9)

where  is the equivalent stress, k_u and k_f are penalty factors.

The permissive velocity field in which the minimum value of functional  was gotten is the true solutions satisfying Eqns.(1-6), that is

                                 (10)

For any weight function ω, the weak-form satisfying equilibrium equations and boundary conditions can be derived from the energy principles for problems of solid mechanics, one of these is the minimum total potential energy principle, and it can be expressed as,

          (11)

where

                  (12)

From Eqn.(11), then we have the following equation,

Ku=f                                     (13)

where  K is system stiffness matrix and f is nodal force vector, and

          (14)

where  B is strain ratio matrix which indicates the relationships between nodal strain ratio vector and nodal velocity vector in the element; δ is the vector symbol of  Kronecker, and δ^T=[1  1  1  0], D is relative matrix of strain ratio.

                     (15)

3 Meshless procedures of metal rheological forming

Meshless procedures of metal rheological forming are as follows:

1) making solution domain and boundary discrete by nodes, establishing approximate functions of meshless;

2) creating background integral cells;

3) determining the number of Gauss-integral point and weight coefficient;

4) cycling background to assembly stiffness matrix and nodal force matrix;

5) solving the system equations to obtain the velocity field and displacement, stress and strain;

6) outputting the data.

The flow process chart is shown in Fig.1.

4 Numerical examples of meshless analysis

In this section, we illustrate some applications of RKPM in forming process simulations to verify our programming and computational methods, taking the compression of circular cylinder as an example and analyzing the influence of node numbers and size factor, the simulation of finite element method was done to compare with. The mould is considered one rigid-body and its punch moves downwards in a constant velocity (as shown in Fig.2).

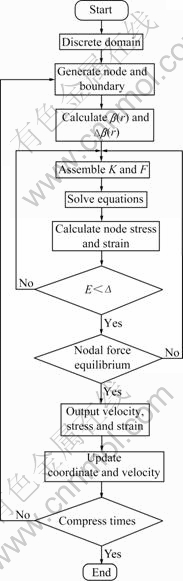
Fig.1 Flow process chart of RKPM programming

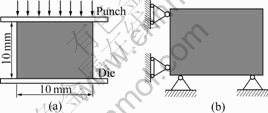
Fig.2 Geometric and mechanical models of blank: (a) Geometric model; (b) Mechanical model

In order to study the influences of node numbers, the numerical values, the domains with 10×10, 15×15, 19×19 and 25×25 nodes, and 2×2 Gauss-integration, the size influence factor 1.0 are chosen. The final deformation under 4 kind of dispersion is shown in Fig.3.

Fig.4 and Fig.5 show the strain field and velocity field in the simulation process under 25×25 nodes dispersing.

The FEM was used to verify the programming. Fig.6 shows the deformation under different downwards of punch’s movement, which only shows the boundary nodes.

Table 1 indicates that the calculation results of FEM and RKPM are approximately, the maximum error is about 1.12% and the minimum is less than 0.75%, and the FEM result is slightly greater than RKPM result.

Fig.7 shows the time consumption of 5 kinds dispersing, and the more the nodes are dispersed, the longer the time is consumed (same computer), which is similar to the finite element method which consumes more time with more nodes. The change of size factor with the same nodes means to change the influence radius of weight functions. The time consumption is shown in Fig.8. It can be concluded that the best size factor range is between 0.7 and 1.2, that is to say, when the influence radius of shape functions equals 0.7-1.2 times the size of background integration cell, the calculation coefficiency is higher. However, the calculation coefficiency is in connection with the nodal dispersing form (ordination or non-ordination), the size of background cell (homogeneous or non-homogeneous) and so on.

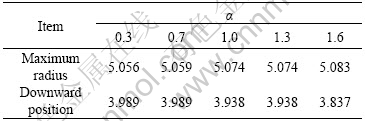
For different size influence factors, the maximum compression radius in the simulation is shown in Table 2, in which the maximum radius error is 0.027, and it is less affected in accuracy. However, it is suggested that the size influence factor should not be too small, or else the stiffness matrix would be odd in the course of calculating, which will result in solution failure. At the same time, the efficiency of calculation would be lower if it is too large.

5 Conclusions

Based on the theory of meshless method to solve larger deformation problem of rigid-plastic, the rheological simulation of cylinder compression is performed by programming. Example shows the feasibility of application in rheological forming by using meshless method, and provides a new idea for the rheological forming of complex volume. The results of meshless method and FEM are very close in the rheological process. The larger deformation can be easily simulated with element-free by changing the nodal radius of influence domain and without remeshing during the calculation. By comparing with FEM, the precision of meshless method is verified, which provides a new numerical calculation for solving rheological forming. The meshless method removes element grid and the

Fig.3 Final forming diagrams under 4 kinds of node dispersing scheme: (a) 10×10 nodes; (b) 15×15 nodes; (c) 19×19 nodes;    (d) 25×25 nodes

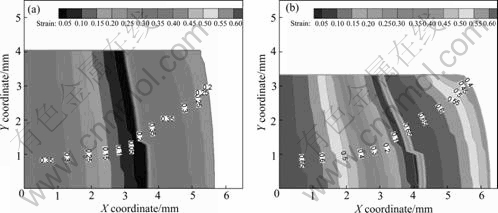
Fig.4 Strain field at different positions under different stages: (a) t=10 s; (b) t=24 s

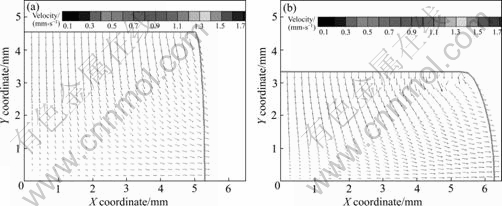
Fig.5 Velocity field at different position under different stages: (a) t=10 s; (b) t=24 s

Table 1 Boundary free nodal radius and its error of FEM and RKPM under different heights

Fig.6 Deformation contrast between FEM and meshless method under different compressed stages: (a) t=10 s; (b) t=16 s; (c) t=24 s

phenomenon of grid torsion is avoided validly during the calculation. However, there is also a need for further consummating and painstaking research on high temperature rheological forming of complex shape parts and its application in practical engineering.

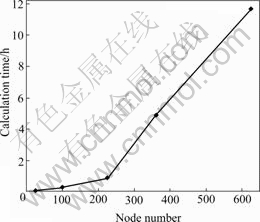
Fig.7 Computing time under different nodes at α=1.0

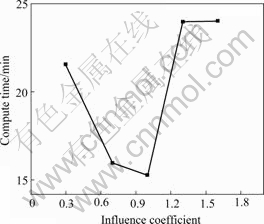
Fig.8 Computing time under different α at nodes of 225

Table 2 Maximum radius under different influence factors

The research on the meshless method such as rapid algorithm of meshless methods, implementing parallel algorithm on the basis of the existing achievement, improving efficiency and so on still needs to study further.

References

[1] ZHANG Xiong, LIU Yan. Meshless method [M]. Beijing: Tsinghua University Press, 2005: 1-2.(in Chinese)

[2] YIN Shui-ping, LUO Ying-she, CAO Zheng, LIU Wen-bin. Study on weight functions efficiency of element-free galerkin method [J]. Natural Science Journal of Xiangtan University, 2007, 29(3): 65-70. (in Chinese)

[3] BELYTSCHKO T, KRONGAUZ Y. Meshless methods: An overview and recent development [J]. Comput Methods Appl Mech Engrg, 1996, 139: 3-47.

[4] ZHANG Y Y. Meshless modelling of crack growth with discrete rotating [J]. Int J Mech Mater Des, 2008, 4: 71-77.

[5] BUI H H, FUKAGAWA R, SAKO K, OHNO S. Lagrangian meshfree particles method (SPH) for large deformation and failure flows of geomaterial using elastic-plastic soil constitutive model [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(12): 1537-1570.

[6] SCHWAIGER H F. An implicit corrected SPH formulation for thermal diffusion with linear free surface boundary conditions [J]. International Journal for Numerical Methods in Engineering, 2008, 75(6): 647-671.

[7] LIU Ya-ling, LIU W K, BELYTSCHKO T, NEELESH P, ALBERT C. Immersed electrokinetic finite element method [J]. International Journal for Numerical Methods in Engineering, 2007, 71(4): 379-405.

[8] BELYTSCHKO T. A coupled finite element-element-free Galerkin method [J]. Comput Mech, 1995, 17: 186-195.

[9] YU Min, LUO Ying-she, LUO Wen-bo, PENG Xiang-hua. Numerical simulation and experiment study on rheological of polypropyleme [J]. J Cent South Univ Technol, 2007, 14(s1): 151-153.

[10] CHEN J S, PAN C, WU C T. A Lagrangian reproducing kernel particle method for metal forming analysis [J]. Comput Mech, 1998, 22(3): 289-307.

[11] ZHAO Zhi-ye, WANG Guo-dong. Modern processing mechanics of plasticity [M]. Shenyang: Northeast College of Technology Press, 1986: 45-140. (in Chinese)

(Edited by CHEN Wei-ping)

Foundation item: Project(02103) supported by the National Education Department of China; Project(200509) supported by the Central South University of Forestry and Technology; Project(07031B) supported by Scientific Research Fund of Central South University of Forestry and Technology; Project supported by the Rewarding Project for Excellent PhD Thesis of Hunan Province, China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: YIN Shui-ping, Master; Tel: +86-731-5623021; E-mail: ysp8293@163.com