­­ New approach for modeling flow stress of aluminum alloy 6A10

considering temperature variation

LI Xue-song(李雪松), WU Lai-zhi(伍来智), CHEN Jun(陈 军), ZHANG Hong-bing(张鸿冰)

National Die and Mold CAD Engineering Research Center, Shanghai Jiao Tong University, Shanghai 200030, China

Received 29 September 2009; accepted 2 February 2010

Abstract:

The flow stress behavior of aluminum alloy 6A10 was studied by the hot compression tests at temperatures from 350 °C to 550 °C and strain rates from 0.1 s^-1 to 10 s^-1 with Gleeble-1500 thermo-mechanical simulator. The result demonstrates that the temperatures of specimen differ from initial ones affected by deformation conditions, and that the softening mechanism is dynamic recovery. A new approach was proposed to analyze the flow stress character directly from actual stress, strain, temperature and strain rate data, without performing any previous flow stress correction caused by temperature variation. Comparisons between the experimental and predicted results confirm that the established flow stress model can give reasonable estimation, indicating that the mentioned approach can be used in flow stress model analysis of the materials that undergo only dynamic recovery based on the data obtained under variable deformation temperature.

Key words:

aluminum alloy 6A10; flow stress model; dynamic recovery;

1 Introduction

Aluminum alloy 6A10 is a newly developed alloy by adjusting the mass ratio of Mg to Si and adding some chemical elements refining gain size based on aluminum alloy 6061[1]. It has higher strength while maintaining good forgeability, surface quality and corrosion resistance, and it is widely used for automobile chassis parts[2]. Flow stress model that relates the flow stress of a material with a known initial microstructure to the strain, strain rate, and temperature of deformation is an essential input for computer modeling thermo- mechanical process using finite element methods. Therefore, obtaining an accurate flow stress model of aluminum alloy 6A10 is significant for forming process designers.

In the past, a number of research groups have attempted to develop flow stress model of aluminum alloys during different plastic deformation processes and conditions. JANSSON et al[3] obtained the properties of aluminum alloys in sheet hydroforming on the identification of parameters for constitutive models. CHEN et al[4] developed an elastoplastic constitutive description of casting aluminum alloys, which can take into account of the effect of both porosity evolution and large deformation. MA and ROTERS[5] developed a new constitutive model based on the dislocation density for single crystal aluminum at elevated temperatures. AIROD et al[6] carried out a series of compression tests to deduce the flow stress model of commercially pure aluminum deformed at room temperature over a wide range of strain rates. ZHANG et al[7] used hot compression testing of a new Al-Mg-Si-Cu aluminum alloys to model their flow stress in high temperature deformation. Although lots of efforts have been put on the deformation behavior of aluminum alloys, more investigations are needed for the new aluminum alloy 6A10 to realize numerical simulation of hot deformation.

It is very common to observe that specimen temperature does not remain absolutely constant, but change throughout the course of test deformation, which will finally induce the change of flow stress. To deal with this problem, most researchers usually conducted an iterative flow stress correction procedure before the constitutive analysis[8-10]. Whereas, this work is going to carry out a series of hot compression tests to develop flow stress model for the aluminum alloy 6A10 directly from the actual stress, strain, temperature and strain rate data, without conducting any previous flow stress correction. The validity of the proposed flow stress model was also analyzed.

2 Experimental

The chemical compositions of aluminum alloy 6A10 are listed in Table 1 and the specimens (d10 mm×15 mm, as shown in Fig.1) used in compression tests were machined from the as-received industrially cast bars with the heat-treatment at 540 °C for 2 h.

Table 1　Chemical compositions of aluminum alloy 6A10 (mass fraction, %)

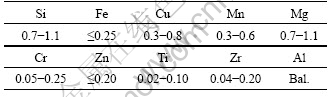
Fig.1 Specimen used in hot compression tests

The compression test conducted on Gleeble-1500 simulator was used to investigate the flow stress behavior of aluminum alloy 6A10. Specimens were heated to 550 °C at a heating rate of 10 °C/s and held for 5 min in order to obtain well-proportioned and homogeneous microstructure. Then, they were cooled to deformation temperatures at a cooling rate of 5 °C /s and homogenized for 30 s to eliminate thermal gradients before deformation was initiated. Four different deformation temperatures (350, 400, 500, 550 °C) and three different strain rates (0.1, 1, 10 s^-1) were used in the compression process, and the total equivalent strain ε was 0.8. Then, specimens were rapidly quenched in water to preserve the microstructure after hot deformation. In order to reduce the friction between the anvils and specimen during compression, tantalum sheet together with graphite powder were used on both sides of the specimen. Because of the high thermal conductivity of aluminum alloy, the temperature measured by a thermo-couple in the deformation zone was close to the mean temperature of specimen and could be used directly.

3 Results

3.1 Change of actual deformation temperatures during compression

Due to the conversion of plastic work into heat and heat losses by conduction, convection, and radiation between the specimen and its surroundings, the actual specimen temperatures differ from the initial ones. At low strain rates, such as 0.1 s^-1 and 1 s^-1, there was enough time for the thermo-couple to achieve actual specimen temperature. However, when the strain rate reached 10 s^-1, the deformation time was so short that the specimen temperature attained lagged behind the actual one because of limited sensitivity of thermo-couple. Therefore, to overcome this difficulty, the incremental procedure[11] was used to calculate the temperature increase during compression at strain rate of 10 s^-1. It was assumed that the temperature rise was uniform throughout the specimen and that the changes in ρ (density) and c (specific heat) during the temperature interval δT could be neglected. The increase in temperature was evaluated using the following expression:

                       (1)

Fig.2 presents the effect of strain rate on deformation temperature at a given initial temperature of 400 °C, which shows that during testing at strain rate of 0.1 s^-1, the deformation temperature decreases by up to ~6 °C as a consequence of chilling of the specimen, whereas during testing at strain rate of 1 s^-1 and 10 s^-1, it increases by up to ~12 °C and ~26 °C, respectively, due to the deformation heat.

Fig.2 Variations of specimen temperatures

3.2 General characteristics of microstructure evolution and equivalent stress—strain curves

Fig.3 and Fig.4 show the typical microstructures of original and as-deformed state of aluminum alloy 6A10, respectively. The original grain structure was equiaxed and the deformed ones elongated perpendicularly to the compression direction (as arrowed in Fig.4) and without any new grains formed, which implied that the softening mechanism of this alloy is dynamic recovery rather than dynamic recrystallization due to its high dislocation energy[12].

In Fig.5, the solid lines show the equivalent stress—strain curves obtained from the tests conducted, and all of the curves are described based on the initial specimen temperature. As can be observed, at low strains, most of the curves present a small hardening transient which subsequently develops into a saturation state. The rate at which this saturation level is achieved depends strongly on deformation temperature and strain rate. The hardening transient is more clearly observed at low deformation temperatures and high strain rates. Also, when saturation is attained, the stress level increases either as the deformation temperature decreases or as the strain rate increases. Besides, for a given test condition, the values of saturation stress do not keep constant, which is caused by the change of deformation temperature as discussed in the last section. On the one

Fig.3 Original grain structure of aluminum ally 6A10

Fig.4 Deformed grain structure of aluminum ally 6A10

Fig.5 Flow stress of aluminum alloy 6A10 under hot compression tests: (a) 350 °C; (b) 400 °C; (c) 500 °C; (d) 550 °C

hand, the increase of temperature induces a drop in flow stress (1 s^-1and 10 s^-1). On the other hand, the decrease of temperature results in an increase of flow stress (0.1 s^-1).

4 Modeling flow stress of aluminum alloy 6A10

4.1 Introduction of flow stress model

SAH et al[13] put forward an exponential-saturation model for equivalent flow stress σ as a function of equivalent strain ε:

              (2)

where σ₀ is the initial flow stress, σ_s is the saturation flow stress, m is a constant and ε_r is the relaxation strain constant, which can be described as follows[14]:

                                (3)

where a and b are material constants.

The relationship among flow stress, strain rate and temperature of metal during hot deformation can be usually expressed as follows[15]:

For low stress level (ασ<0.8),           (4)

For high stress level (ασ<1.2),      (5)

For all stress level,

 (6)

where A₁, A₂, A, n₁, n, α, β are material constants, which are independent of the deformed temperatures;  is the strain rate (s^-1); R is the gas constant (8.31 J/(mol?K)); T is the absolute temperature (K); Q is the activation energy of hot deformation (J/mol); and σ is the stress at any constant strain (MPa). The relationship among the value of α, β and n is as follows

α=β/ n                                      (7)

ZENER and HOLLOMON[16] proposed an expression describing the relationship between the temperature and strain rate as follows:

                           (8)

where Z is Zener-Hollomon parameter, which is a factor of strain rate compensated by temperature (s^-1).

Over the whole stress range, substituting Eq.(6) into Eq.(8) gives

               (9)

Based on Eq. (9), the flow stress σ can be written as a function of Zener-Hollomon parameter, considering the definition of the hyperbolic sine law.

           (10)

4.2 Modeling initial flow stress σ₀ of aluminum alloy 6A10

The equivalent stress-strain data obtained from compression tests under different strain rate and different initial temperature conditions can be used to determine material constants in flow stress model.

Taking the logarithm of both sides of Eqs.(4) and (5), respectively, the mean value of n₁ can be calculated as 6.04 at low stress level (for temperature of 500, 550 °C) from the slope of -lnσ plot (Fig.6), and the mean value of β as 0.31 MPa^-1 at high stress level (for temperature of 350, 400 °C) from the slope of -σ plot (Fig.7). In order to determine the value of α, the value of n=n₁ was taken as a first approximation in Eq.(7), and α=β/n=0.052 MPa^-1.

Fig.6 Relationship between  and lnσ

Fig.7 Relationship between  and σ

Taking the logarithm and partial derivative of both sides of Eq.(9),  is plotted against ln[sinh(ασ)] as shown in Fig.8, and ln[sinh(ασ)] is plotted against 1/T as shown in Fig.9, respectively. It is shown that n and lnA-Q/(RT) are responding to the slope and intercept of the lines in Fig.8, respectively, and Q/(Rn) is responding to the slope of the lines in Fig.9. Therefore, the mean values of n, A and Q can be easily obtained as 4.98, 6.95×10⁹ s^-1 and 166.08 kJ/mol, respectively.

Fig.8 Relationship between  and ln[sinh(ασ)]

Fig.9 Relationship between ln[sinh(ασ)] and 1/T

Then, the value of n was substituted into Eq.(7) and iterated to obtain the optimum values of α, n，Q and A, until the standard deviation of n reached the minimum value. These optimized parameters are given in Table 2.

Table 2 Parameters in initial flow stress and saturation stress model of aluminum alloy 6A10

4.3 Modeling of saturation stress σ_s of aluminum alloy 6A10

If it is assumed that at a large effective strain (e.g. ε≥0.6), saturation state has been achieved, and the flow stress, temperature and strain rate data would allow the evaluation of the flow stress behavior of the alloy under saturation conditions. However, the procedure of modeling initial flow stress described in last section was not suitable for modeling saturation stress, as the deformation temperature corresponding to saturation stress was not constant. As saturation stress, strain rate, and temperature data are precisely known, the incorporation of these data into Eq.(10) for the evaluation of the saturation behavior of the model is possible. All the parameters involved can be readily determined by means of non-linear least squares analysis. Table 2 summarizes the results obtained and Fig.10 illustrates the graphical representation of the data. As expected, the model provides a satisfactory description of the data in the range of conditions explored.

Fig.10 Comparison between experimental values of saturation flow stress and those predicted

4.4 Fitting and verification of flow stress model of aluminum alloy 6A10

After modeling both initial stress and saturation stress of aluminum alloy 6A10, the flow stress model requires the simultaneous determination of three other parameters, a and b (Eq.(3)), and m (Eq.(2)). The different parameters involved in the model under consideration can be readily determined by minimizing the quadratic difference between the experimental values of the flow stress and those predicted by the model, that is to say,

                   (11)

The optimized values of a, b and m were achieved as 0.07, 1.2×10^-5 and 0.5, respectively. Finally, the flow stress model of aluminum alloy 6A10 is summarized as follows:

          (12)

The symbols in Fig.5 illustrate the results obtained with the application of the model for the description of the experimental data, which shows that in general, such an approach provides a satisfactory outcome. Major differences between the predicted and the experimental data are found under deformation conditions at 350 °C and 10 s^-1, 400 °C and 1 s^-1, and 500 °C and 0.1 s^-1. The deviations are not observed to be systematic error because the model predicts either an overestimation or an underestimation of the experimental flow stress, depending on the deformation condition considered.

As can be observed in Fig.5, the model is able to show the trend of the experimental data quite satisfactorily. Particularly, when the material is deformed at elevated strain rates, the deformation temperature rises obviously due to the deformation heat, which also induces a drop in the flow stress. This phenomenon could be predicted preferably by this model.

5 Conclusions

1) During the process of hot compression tests for aluminum alloy 6A10, the temperatures of specimen are different from initial ones, due to the effect of both deformation heat and the heat exchange between specimen and its surroundings. At low strain rates (0.1 s^-1), specimen temperatures are lower than initial ones, inducing the rise of flow stress. While at high strain rates (1 s^-1 and 10 s^-1), specimen temperatures are higher than initial ones, resulting in the drop of flow stress.

2) The flow stress description of aluminum alloy 6A10 under dynamic recovery was analyzed by a new approach based on an exponential-saturation model, which was conducted from the actual stress, strain, temperature, and strain rate without performing any previous flow stress correction, and the model finally provided satisfactory results. It is concluded that the new approach is suitable for flow stress model analysis of the materials that undergo only dynamic recovery considering deformation temperature variation.

References

[1] SHAO Guang-jie, ZHANG Heng-hua, XU Luo-ping. Progress on aluminum alloys and their heat treatment for automobile materials [J]. Metal Heat Treatment, 2004, 29(1): 29-32.

[2] CHOI Y, YEO H T, PARK H J, OH G H, PARK S W. A study on press forming of automotive sub-frame parts using extruded aluminum profile [J]. Journal of Materials Processing Technology, 2007, 187/188: 85-88.

[3] JANSSON M, NILSSON L, SIMONSSON K. On constitutive modeling of aluminum alloys for tube hydroforming applications [J]. International Journal of Plasticity, 2005, 21: 1041-1058.

[4] CHEN B, PENG X, FAN J, CHEN S. A constitutive description for casting aluminum alloy A104 based on the analysis of cylindrical and spherical void models [J]. International Journal of Plasticity, 2005, 21: 2232-2253.

[5] MA A, ROTERS F. A constitutive model for fcc single crystals based on dislocation densities and its application to uniaxial compression of aluminium single crystals [J]. Acta Materialia, 2004, 52: 3603-3612.

[6] AIROD A, VANDEKINDEREN H, BARROS J, COLAS R, HOUBAERT Y. Constitutive equations for the room temperature deformation of commercial purity aluminum [J]. Journal of Materials Processing Technology, 2003, 134: 398-404.

[7] ZHANG Hui, LI Luo-xing, YUAN Deng, PENG Da-shu. Hot deformation behavior of the new Al-Mg-Si-Cu aluminum alloy during compression at elevated temperatures [J]. Materials Characterization, 2007, 58(2): 168-173.

[8] LAASRAOUI A, JONAS J J. Prediction of steel flow stresses at high temperature and strain rates [J]. Metallurgical Transactions A, 1991, 22: 1545-1558.

[9] WU Wen-xiang, SUN De-qing, CAO Chun-yan, WANG Zhan-feng, ZHANG Hui. Flow stress behavior of 5083 aluminium alloy under hot compression deformation [J]. The Chinese Journal of Nonferrous Metals, 2007, 17(10): 1667-1671. (in Chinese)

[10] CARMONA R, ZHU Q, SELLARS C M, BEYNON J H. Controlling mechanisms of deformation of AA5052 aluminum alloy at small strains under hot working conditions [J]. Materials Science and Engineering A, 2005, 393(1/2):157-163.

[11] KOBAYASHI S, OH S I, ALTAN T. Metal Forming and the finite element method [M]. Oxford: Oxford University Press, 1989.

[12] WANG Zhu-tang, TIAN Rong-zhang. Aluminum alloys and manual of its manufacture [M]. Changsha: Central South University Press, 2005:127-130. (in Chinese)

[13] SAH J P, RICHARDSON G J, SELLARS C M. Recrystallization during hot deformation of nickel [J]. Journal of Australian Institute of Metals, 1969, 14(4): 292-297.

[14] SHI H, MCLAREN A J, SELLARS C M, SHAHANI R, BOLINGBROKE R. Constitutive equations for hot flow stress of aluminum alloys [J]. Materials Science and Technology, 1997 (13): 210-216.

[15] JONAS J, SELLARS C M, TEGART W J, MC G. Strength and structure under hot working condition [J]. International Metal Reviews, 1969, 14(130):1-24.

[16] ZENER C, HOLLOMON J H. Effect of strain rate upon the plastic flow of steel [J]. Journal of Applied Geophysics, 1944, 15(1): 22-32.

(Edited by LI Xiang-qun)