Trans. Nonferrous Met. Soc. China 23(2013) 2361-2367
Phase field simulation for non-isothermal solidification of multicomponent alloys coupled with thermodynamics database
Shu-zhou ZHANG1, Rui-jie ZHANG1, Xuan-hui QU1,2, Wei FANG1, Ming-zhi LIU1
1. School of Materials Science and Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. State Key Laboratory for Advanced Metal and Materials, University of Science and Technology Beijing, Beijing 100083, China
Received 10 July 2012; accepted 16 April 2013
Abstract:
In order to quantitively model the real solidification process of industrial multicomponent alloys, a non-isothermal phase field model was studied for multicomponent alloy fully coupled with thermodynamic and diffusion mobility database, which can accurately predict the phase equilibrium, solute diffusion coefficients, specific heat capacity and latent heat release in the whole system. The results show that these parameters are not constants and their values depend on local concentration and temperature. Quantitative simulation of solidification in multicomponent alloys is almost impossible without such parameters available. In this model, the interfacial region is assumed to be a mixture of solid and liquid with the same chemical potentials, but with different composition. The anti-trapping current is also considered in the model. And this model was successfully applied to industrial Al-Cu-Mg alloy for the free equiaxed dendrite solidification process.
Key words:
phase-field; multicomponent alloys; coupling; thermodynamics; non-isothermal solidification; simulation;
1 Introduction
The phase-field model becomes a powerful tool which can describe the complex interface pattern evolutions [1-5]. It describes the microstructure using a set of conserved and nonconserved field variables that are continuous across the interface regions. Phase field models of solidification have been originally developed for pure materials [6,7] and then extended to alloys [8-11]. Since industrial alloys are almost multi- component alloys and contain more than two main solutes, phase field models are then extended to multicomponent systems [12-16]. But most of the phase field models for alloys solidification are under the isothermal assumption and do not consider the latent heat release [17,18]. Recently, the non-isothermal phase field models for alloy solidification [19-22] are also developed, but none of them is fully coupled with thermodynamics database, especially for the thermal transportation equations.
In multicomponent alloys, phase equilibrium, solute diffusion behaviors and latent heat release are no longer the same as that in binary alloys because of solute interactions. A convenient way to solve this problem is coupling the solidification model with thermodynamic and diffusion mobility database [23,24]. Thus, phase equilibrium, solute diffusion transportation and latent heat release can be accurately predicted. There has been a great effort in the past years concerned with the assessment of thermodynamic and diffusion mobility database in multicomponent alloys [25-27].
In this work, we develop a non-isothermal phase field model for multicomponent alloy fully coupled with thermodynamic and diffusion mobility database to quantitively model the real solidification process of industrial multicomponent alloys. Furthermore, industrial Al-Cu-Mg alloy is taken as an example to study the free equiaxed dendrite solidification process by this model.
2 Non-isothermal phase-field model for multicomponent alloys
2.1 Governing equations
The total free energy of the system is defined as
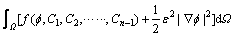(1)
where F is the total free energy of the system, f is the free energy density, W is the volume integration on space, e is the gradient energy coefficient and 
is the phase field ranging from zero in liquid to one in solid.
In this work, the free energy density is defined as [28]
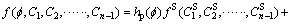
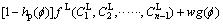(2)
where
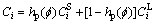(3)
where S is the solid phase, L is the liquid phase and hp is a mixing function for phase; the equilibrium compositions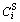 
and 
in a given point are not independent of each other, but restricted by the same chemical potential condition; where hp() and g() are given as
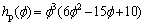(4)
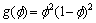(5)
Then the governing equations for the phase-field can be expressed as [29]
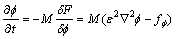(6)
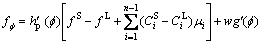(7)
where M is the phase-field mobility and mi is the chemical potential of the ith solute.
The time evolution of diffusion field under mass conservation condition can be given by
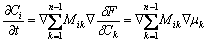(8)
where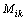 
is the diffusion mobility. If the diffusion mobility follows a mixture rule assumed as
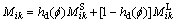(9)
where hd is a mixing function for diffusion, the Eq. (8) for diffusion field can be re-written as
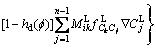(10)
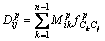(11)
where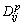 
is the diffusion coefficient in solid (p = S) or liquid (p=L) phase. Under the assumption that 
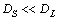, we can re-write the diffusion equation as
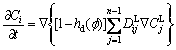(12)
In order to eliminate chemical potential jump [30] effect, an antitrapping term should be introduced into the diffusion equation:
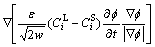(13)
where
(14)
Using the energy conservation law, the thermal diffusion equation can be described as
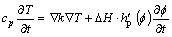(15)
where T is temperature, k is thermal conductivity, DH is the latent heat, cp is specific heat capacity and can also be described by the mixture rule:
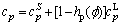(16)
Now, the evolution of phase field, solute concentration field and temperature field are governed by Eq. (6), Eq. (13) and Eq. (15), respectively. The phase field control and solute field control equation using explicit difference algorithm is named as Euler method. And the temperature control equation using alternating direction implicit method is also referred to the ADI method. In this work, the phase equilibrium between solid and liquid in Eq. (3) and (7), chemical potentials in Eq. (7), solute diffusion coefficients in Eq. (12) and (13), latent heat in Eq. (15) and specific heat capacity in Eq. (16) can be gotten by fully coupling with the thermodynamics and diffusion mobility database, which will be shown in Section 3.
2.2 Phase-field parameters
In the phase-field equation, there are three parameters: phase-field mobility M, gradient energy coefficient e and height of the parabolic potential w. w and e can be obtained from the interfacial energy s and the interface width 2l using the one-dimension equilibrium solution [29]:
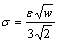(17)
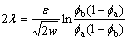(18)
where the interface 2l is defined as the width over which changes from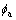 
to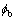 
.
The phase-field mobility M is correlated with the interface kinetics and its equation can be given as [29]
(19)
If a infinite interface mobility is applied [31], which is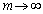 
, the phase-field mobility can be expressed as [31]
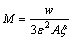(20)
where
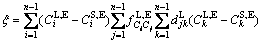(21)
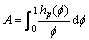(22)
where E is the equilibrium state.
3 Thermodynamics and diffusion description in multicomponent alloys
3.1 Thermodynamics
In the case of multicomponent alloys, integral Gibbs energy for each phase depends on its constitution, temperature and pressure, and this can be described by a thermodynamic model [32] as
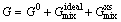(23)
where 
is the contribution of pure components of phase to the Gibbs energy,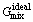 
is the ideal mixing contribution and 
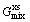is the contribution due to non-ideal interaction between components, also known as the Gibbs excess energy of mixing. When Gibbs energy in Eq. (23) is obtained, the other thermodynamics related parameters, such as phase equilibrium concentration, chemical potential, latent heat and specific heat capacity, can all be calculated out accurately, for example:
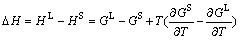(24)
and 
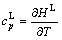(25)
There are a large number of thermodynamic models for various substances in different state [33]. For example, for FCC, BCC, HCP solid solution phases and liquid phase, the Gibbs energy G, for ternary alloy can be written as [34]
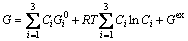(26)
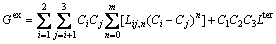(27)
Such work has been proved powerful, since there are several available software systems which are capable of estimating the phase equilibrium as a function of pressure, temperature and the composition of alloying elements, such as Thermo-Calc [35], PANDAT [36], and MTDATA [37]. In this work, the properties of thermodynamics are all obtained by Thermo-Calc through TQ interface. The thermodynamic description of Al-Cu-Mg system will be shown in Section 4.
3.2 Diffusion coefficients
For the case that the elements are substitutional, the diffusion coefficient defined in the volume-fixed frame of reference,
, can be expressed as [38]
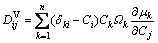(28)
where Ci is the mole fraction of component i,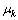 
is the chemical potential of component k, and 
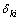is the Kronecker delta. It can be observed that the 
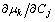is a purely thermodynamic parameter which corresponding to the thermodynamic factor and can thus be evaluated from the thermodynamic description of the system. The parameter 
is the mobility of specie k in a given phase and will be discussed later.
The chemical diffusion coefficients, by eliminating the concentration element n, can be deduced as
(29)
where n is the solvent and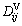 
is given in equation (28). The diffusivity 
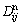is the most convenient one for practical calculations. Determination of the diffusion mobility parameter in Eq. (28) requires the use of experimental diffusion data. Tracer or self diffusivity 
, is generally determined from diffusion studies using isotopes and directly related to the mobility by means of the Einstein relation as
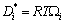(30)
Using the diffusion coefficient expression in Eq. (29), the concentration of element n is eliminated and an (n-1)×(n-1) chemical diffusion matrix is obtained. Then the concentration dependent solute diffusion coefficients in Eq. (13) can also be accurately obtained.
It is worth noting here that the thermodynamic factors in Eq. (28) are also obtained by Thermo-Calc through the TQ interface.
4 Application to Al-Cu-Mg alloy
The thermodynamic description of Al-Cu-Mg system now can be used from BUHLER et al [39]. Using the parameters for the thermodynamic description of Al-rich ternary Al-Cu-Mg alloys, 
for liquid phase can be evaluated as
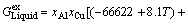
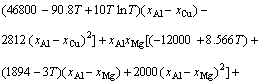
(31)
For Al-FCC primary solution,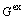 
is given by
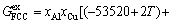
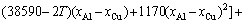
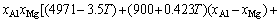
(32)
Tracer diffusion is the diffusion of a tracer in the matrix of an alloy. The impurity or self diffusivity , in ternary Al-Cu-Mg is given in Table 1. The other parameters used in the simulation are given in Table 2.
Table 1 Diffusion data used in simulation
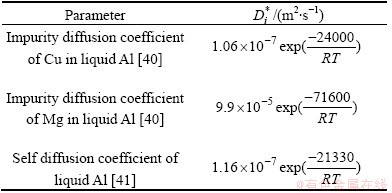
Table 2 Parameters used in simulation
Figures 1(a) and (b) show the temperature field and phase field in the whole system, respectively. The solidification time is 4.5×10-5 s. Figures 1(c) and (d) show the concentration field of Cu and Mg, respectively, both in solid and liquid. They show that the temperature field has less gradient than concentration fields since the thermal conductivity is almost 103 times larger than the solutes diffusion coefficients.
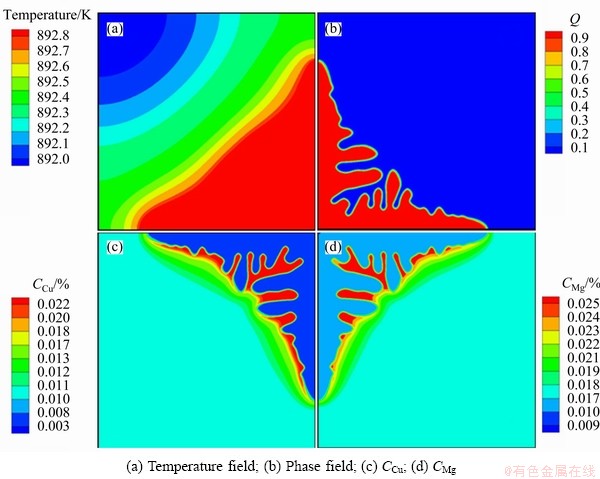
Fig. 1 Simulation results of Al-1.1% Cu-1.8% Mg dendritic solidification process (t= 4.5×10-5 s)
Figure 2 shows the distribution of diffusion coefficients in the whole system. It shows that the diffusion coefficients are all highly concentration dependent, both diagonal (DCuCu and DMgMg) and off-diagonal (DCuMg and DMgCu). It shows that the off-diagonal diffusion coefficients (DCuMg and DMgCu) are about 10% of diagonal ones (DCuCu and DMgMg).
Figure 3 shows the latent heat and specific heat capacity distribution in the whole simulation area. It shows that the latent heat and specific heat capacity are both concentration and temperature dependent. They both change a lot in the whole system. It is almost impossible to get these parameters accurately if the model is not coupled with thermodynamics database. Quantitative simulation of solidification in multi- component alloys is also impossible without such parameters available.
5 Conclusions
1) A non-isothermal phase field model was developed for multicomponent alloy fully coupled with thermodynamic and diffusion mobility database, which can accurately predict the phase equilibrium, solute diffusion coefficients, specific heat capacity and latent heat release in the whole system.
2) These parameters are not constants and their values are dependent on local concentration and temperature. Quantitative simulation of solidification in multicomponent alloys is almost impossible without such parameters available.
3) In the model, the interfacial region is assumed to be a mixture of solid and liquid with the same chemical potentials, but the different compositions.
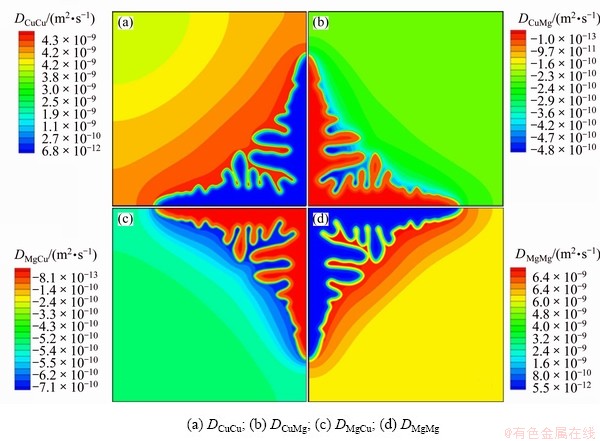
Fig. 2 Diffusion coefficients distribution at solidification time 4.5×10-5 s
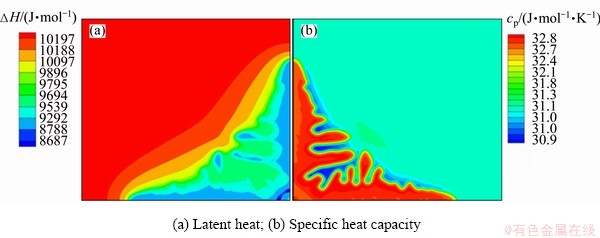
Fig. 3 Latent heat and specific heat capacity distribution at solidification time 4.5×10-5 s
4) The anti-trapping current is also considered in the model. For example, industrial Al-Cu-Mg alloy for the free equiaxed dendrite solidification process can be studied by the above model.
References
[1] ASTA M, BECKERMANN C, KARMA A, KURZ W, NAPOLITANO R, PLAPP M, PURDY G, RAPPAZ M, TRIVEDI R. Solidification microstructures and solid-state parallels: Recent developments, future directions [J]. Acta Materialia, 2009, 57: 941-971.
[2] BOETTINGER W J, Coriell S R, GREER A L, KARMA A, KURZ W, RAPPAZ M, TRIVEDI R. Solidification microstructures: recent developments, future directions [J]. Acta Materialia, 2000, 48: 43-70.
[3] ZHAO Y, CHEN Z, LU Y L, ZHANG L P. Microscopic phase-field study on aging behavior of Ni75Al17Zn8 alloy [J]. Transactions of Nonferrous Metals Society of China, 2010, 20: 675-681.
[4] CHEN L Q. Phase-field models for microstructure evolution [J]. Annual Review Materials Research, 2002, 32: 113-140.
[5] LONG W Y, CAI Q Z, CHEN L L, WEI B K. Phase-field simulations of solidification of Al-Cu binary alloys [J]. Transactions of Nonferrous Metals Society of China, 2004, 14: 291-296.
[6] MCFADDEN G B, WHEELER A A, BRAUN R J, CORIELL S R, SEKERKA R F. Phase-field models for anisotropic interfaces [J]. Physical Review E, 1993, 48: 2016-2024.
[7] KARMA A, RAPPEL W J. Phase-field model of dendritic sidebranching with thermal noise [J]. Physical Review E, 1999, 60: 3614-3625.
[8] WARREN J A, BOETTINGER W J. Prediction of dendritic growth and microsegregation patterns in a binary alloy using the phase-fleld method [J]. Acta Metall. Mater, 1995, 43: 689-703.
[9] LI X Z, GUO J J, SU Y Q, WU S P, FU H Z. Phase-field simulation of dendritic growth for binary alloys with complicate solution models [J]. Transactions of Nonferrous Metals Society of China, 2005, 15, 769-776.
[10] ECHEBARRIA B, FOLCH R, KARMA A, PLAPP M. Quantitative phase-field model of alloy solidification [J]. Physical Review E, 2004, 70: 061604.
[11] ZHU C S, XIAO R Z, WANG Z P, FENG L. Numerical simulation of recalescence of 3-dimensional isothermal solidification for binary alloy using phase-field approach [J]. Transactions of Nonferrous Metals Society of China, 2009, 19: 1286-1293.
[12] NESTLER B, GARCKE H, STINNER B. Multicomponent alloy solidification: Phase-field modeling and simulations [J]. Physical Review E, 2005, 71: 041609.
[13] WANG J W, ZHU C S, WANG Z P, FENG L, XIAO R Z. Phase-field simulation of forced flow effect on random preferred growth direction of multiple grains [J]. Transactions of Nonferrous Metals Society of China, 2011, 21: 1620-1626.
[14] CHA P R, YEON D H, YOON J K. A phase field model for isothermal solidification of multicomponent alloys [J]. Acta Materialia, 2001, 49: 3295-3307.
[15] QIN R S, WALLACH E R. A phase-field model coupled with a thermodynamic database [J]. Acta Materialia, 2003, 51: 6199-6210.
[16] WANG G, ZENG D C, LIU Z W. Phase field calculation of interface mobility in a ternary alloy [J]. Transactions of Nonferrous Metals Society of China, 2012, 22: 1711-1716.
[17] WHEELER A A, BOETTINGER W J, MCFADDEN G B. Phase-field model for isothermal phase transitions in binary alloys [J]. Physical Review A, 1992, 45: 7424-7439.
[18] WANG J C, YANG G C. Phase-field modeling of isothermal dendritic coarsening in ternary alloys [J]. Acta Materialia, 2008, 56: 4585-4592.
[19] ROSAM J, JIMACK P K, MULLIS A M. An adaptive, fully implicit multigrid phase-field model for the quantitative simulation of non-isothermal binary alloy solidification [J]. Acta Materialia, 2008, 56: 4559-4569.
[20] FABRIZIO M, GIORGI C, MORRO A. A thermodynamic approach to non-isothermal phase-field evolution in continuum physics [J]. Physica D, 2006, 214: 144-156.
[21] LOGINOVA I, AMBERG G, AGREN J. Phase-field simulations of non-isothermal binary alloy solidification [J]. Acta Materialia, 2001, 49: 573-581.
[22] RAMIREZ J C, BECKERMANN C, KARMA A, DIEPERS H J. Phase-field modeling of binary alloy solidification with coupled heat and solute diffusion [J]. Physical Review E, 2004, 69: 51607.
[23] KOBAYASHI H, ODE M, KIM S G, KIM W T, SUZUKI T. Phase-field model for solidification of ternary alloys coupled with thermodynamic database [J]. Scripta Materialia, 2003, 48: 689-694.
[24] ZHANG R J, JING T, JIE W Q, LIU B C. Phase-field simulation of solidification in multicomponent alloys coupled with thermodynamic and diffusion mobility databases [J]. Acta Materialia, 2006, 54: 2235-2239.
[25] SUNDMAN B, JANSSON B, ANDERSSON J O. The Thermo-Calc databank system [J]. Calphad, 1985, 9: 153-190.
[26] LUKAS H L, FRIES S G. Demonstration of the use of "BINGSS" with the Mg-Zn system as example [J]. Journal of Phase Equilibria, 1992, 13: 532-542.
[27] HILLERT M. The compound energy formalism [J]. Journal of Alloys and Compounds, 2001, 320: 161-176.
[28] KIM S G, KIM W T, SUZUKI T. Phase-field model for binary alloys [J]. Physical Review E, 1999, 60: 7186-7197.
[29] KIM S G. A phase-field model with antitrapping current for ulticomponent alloys with arbitrary thermodynamic properties [J]. Acta Materialia, 2007, 55: 4391-4399.
[30] KARMA A. Phase-field formulation for quantitative modeling of alloy solidification [J]. Physical Review Letters, 2001, 87: 115701.
[31] KIM S G, KIM W T, SUZUKI T. Interfacial compositions of solid and liquid in a phase-field model with finite interface thickness for isothermal solidification in binary alloys [J]. Physical Review E, 1998, 58: 3316-3323.
[32] SAUNDERS N. A review and thermodynamic assessment of the Al-Mg and Mg-Li systems [J]. Calphad, 1990, 14: 61-70.
[33] HWANG J Y, BANERJEE R, DOTY HW, KAUFMAN M J. The effect of Mg on the structure and properties of type 319 aluminum casting alloys [J]. Acta Material, 2009, 57: 1308-1317.
[34] PAN X M, LIN C, MORRAL J E, BRODY H D. An assessment of thermodynamic data for the liquid phase in the Al-Rich corner of the Al-Cu-Si system and its application to the solidification of a 319 alloy [J]. Journal of Phase Equilibria and Diffusion, 2005, 26: 225-233.
[35] ANDERSSON J O, HELANDER T, 
L, SHI P F, SUNDMAN B. Thermo-Calc & Dictra, computational tools for materials science [J]. Calphad, 2002, 26: 273-312.
[36] CHEN S L, DANIEL S, ZHANG F, CHANG Y A, YAN X Y, XIE F Y, SCHMID-FETZER R, OATES W A. The PANDAT software package and its applications [J]. Calphad, 2002, 26: 175-188.
[37] DAVIES R H, DINSDALE A T, GISBY J A, ROBINSON J A J, MARTIN S M. MTDATA-thermodynamic and phase equilibrium software from the national physical laboratory [J]. Calphad, 2002, 26: 229-271.
[38] ANDERSSON J O, 
J, APPL J. Models for numerical treatment of multicomponent diffusion in simple phases [J]. Journal of Applied Physics, 1992, 72: 1350-1355.
[39] BUHLER T, FRIES S G, SPENCER P J, LUKAS H L. Phase equilibria of the Cu-In system II: Thermodynamic assessment and calculation of phase diagram [J]. Journal of Phase Equilibria, 1998, 19: 317-333.
[40] DU Y, CHANG Y A, HUANG B Y, GONG W P, JIN Z P, XU H H, YUAN Z H, LIU Y, HE Y H, XIE F Y. Diffusion coefficients of some solutes in fcc and liquid Al: critical evaluation and correlation [J]. Materials Science and Engineering A, 2003, 363: 140-151.
[41] CHERNE F J, DEYMIER P A. Calculation of the transport properties of liquid aluminum with equilibrium and non-equilibrium molecular dynamics [J]. Scripta Materialia, 2001, 45: 985-991.
多元合金耦合热力学数据非等温凝固的相场模拟
章书周1，张瑞杰1，曲选辉1,2，方 伟1，刘明治1
1. 北京科技大学 材料科学与工程学院，北京 100083；
2. 北京科技大学 新金属材料国家重点实验室，北京 100083
摘 要：研究一种多元合金的非等温相场模型，定量地模拟工业多元合金的真实凝固过程，结合热力学和扩散迁移率的数据来预测整个系统中的相平衡、溶质扩散系数、比热容和放出的潜热。结果表明：这些参数不是常数，它们的值与成分和温度有关。没有这些参数，定量模拟多元合金的凝固几乎是不可能。在这个模型中，界面区域假设是由有同样化学势的固相和液相混合而成的，但组成不同。这个模型中同样考虑反溶质截流。一并将模型应用到工业Al-Cu-Mg合金的各向枝晶自由长大的凝固过程。
关键词：相场；多元合金；耦合；热力学；非等温凝固；模拟
(Edited by Chao WANG)
Foundation item: Project (2011CB606306) supported by the National Basic Research Program of China; Project (51101014) supported by the National Natural Science Foundation of China
Corresponding author: Rui-jie ZHANG; Tel: +86-10-82377286; E-mail: zhruijie@gmail.com
DOI: 10.1016/S1003-6326(13)62742-9
Abstract: In order to quantitively model the real solidification process of industrial multicomponent alloys, a non-isothermal phase field model was studied for multicomponent alloy fully coupled with thermodynamic and diffusion mobility database, which can accurately predict the phase equilibrium, solute diffusion coefficients, specific heat capacity and latent heat release in the whole system. The results show that these parameters are not constants and their values depend on local concentration and temperature. Quantitative simulation of solidification in multicomponent alloys is almost impossible without such parameters available. In this model, the interfacial region is assumed to be a mixture of solid and liquid with the same chemical potentials, but with different composition. The anti-trapping current is also considered in the model. And this model was successfully applied to industrial Al-Cu-Mg alloy for the free equiaxed dendrite solidification process.
