- Abstract:
- 1 Introduction▲
- 2 Description of cellular...▲
- 3 Model of cellular autom...▲
- 4 Results and discussion▲
- 5 Conclusions▲
- References
- Figure
- Fig.1 Relationship between ln θ0 and
- Fig.2 Relationship between ln θ0 and 1/T
- Fig.3 Comparison between predicted and experimental results
- Fig.4 CA simulation results of influence of strain rate on DRX for aluminium alloy 7050 during hot deformation at temperature of 450 ?C and strain of 5: (a) 1 s-1; (b) 0.1 s-1; (c) 0.05 s-1; (d) 0.01 s-1
- Fig.5 CA simulation results of influence of temperature on DRX of aluminium alloy 7050 during hot deformation at strain rate of 0.01 s-1 and strain of 5: (a) 350 ℃; (b) 400 ℃; (c) 420 ℃; (d) 450 ℃
- Fig.6 Influence of stain rate and temperature on percentage of DRX of aluminium alloy 7050: (a) t=450 ℃; (b) 0.01 s-1
- Fig.7 Influence of strain rate and deformation temperature on mean grain size of aluminium alloy 7050: (a) t=450 ℃; (b) 0.01 s-1
- Fig.8 Influence of strain rate and deformation temperature on mean size of R-grains: (a) t=450 ℃; (b) 0.01 s-1
J. Cent. South Univ. Technol. (2009) 16: 0018-0024
DOI: 10.1007/s11771-009-0003-9![]()
Simulation of dynamic recrystallization for aluminium alloy 7050 using cellular automaton
HUANG Shi-quan(黄始全)1, 2, YI You-ping(易幼平)1, 2, LIU Chao(刘 超)1, 2
(1. Key Laboratory of Modern Complex Equipment Design and Extreme Manufacturing, Ministry of Education,
Central South University, Changsha 410083, China;
2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
Abstract:
The prediction of microstructure evolution plays an important role in the design of forging process. In the present work, the cellular automaton (CA) program was developed to simulate the process of dynamic recrystallization (DRX) for aluminium alloy 7050. The material constants in CA models, including dislocation density, nucleation rate and grain growth, were determined by the isothermal compress tests on Gleeble 1500 machine. The model of dislocation density was obtained by linear regression method based on the experimental results. The influences of the deformation parameters on the percentage of DRX and the mean grain size for aluminium alloy 7050 were investigated in details by means of CA simulation. The simulation results show that, as temperature increases from 350 to 450 ℃ at a strain rate of 0.01 s-1, the percentage of DRX also increases greatly and the mean grain size decreases from 50 to 39.3 μm. The mean size of the recrystallied grains (R-grains) mainly depends on the Zener-Hollomon parameter. To obtain fine grain, the desired deformation temperature is determined from 400 to 450 ℃.
Key words:
aluminium alloy 7050; dynamic recrystallization; cellular automaton;
1 Introduction
Dynamic recrystallization (DRX) is a common phenomenon by which the materials undergo a reduction in the density of accumulated dislocations during plastic deformation for most metals and alloys. It has a great influence on the mechanical properties of the processed materials. The control of the microstructure evolution during hot deformation is important to ensure the mechanical properties of the product in forging process. Aluminium alloy 7050 is an excellent structural material with high strength and toughness and is widely used in aviation industry. The properties of this alloy depend on the fine grains, which can be obtained by means of optimizing the forging progress parameters. In the past, various attempts have been made to numerically simulate the DRX processes, i.e., Monte Carlo (MC) and cellular automaton (CA) method [1-4]. ROLLETT et al [5] and PEZAK et al [6-7] investigated the DRX using MC method in details, in which the hot deformation parameters were not considered. Compared with MC method, the CA method is more veridical and flexible in simulating the DRX process. DING and GUO [8] simulated the microstructure evolution and the flow stress using CA method coupled with the fundamental metallurgical principles. The influence of deformation parameters on the level of DRX was investigated in their work. XIAO et al [9] and JIN et al [10] investigated the influence of the neighbourhood and the distortion of cells on DRX using CA method. However, little work was reported on prediction of the microstructure evolution of aviation material in forging process using the CA method. The CA models used before have not been adopted to simulate the complicated process with varing strain rate and temperature.
The objective of this work is to simulate the microstructure evolution for aluminium alloy 7050 forging using the CA method. To determine the material models, the isothermal compress tests of aluminium alloy 7050 were performed on Gleeble 1500 machine. The microstructure evolution of DRX was predicted by the CA method under different deformation parameters. Furthermore, the influences of forging parameters, such as the deformation temperature, the strain rate and the strain, on DRX percentage and mean grain size of this alloy, were investigated.
2 Description of cellular automaton
The CA method characterized by discrete and synchronic calculation in space-time can be used to describe the evolution law in discrete space-time in a physical system. CA is an array of continuous cells that may be arranged in one, two or three dimensions. In most cases, the grid of 2-D CA can be triangle, square or regular hexagon. Two types of neighbourhood, von Neumann and Moore, are mostly used. Four key elements are necessary for modelling CA: the cell space, the neighbourhood type, the boundary conditions, and the cell state.
In this work, 2-D square grid and Von Neumann neighbourhood were employed. The cells of CA have certain attributes associated with the thermo-mechanical processes that determine the state of a cell such as the recrystallized or the unrecrystallized. The cell state changes dynamically and the state of a cell at time t+?t is determined by the states of both itself and its neighbours at time t through a transition rule. A state variable X can be expressed as
![]() (1)
(1)
where ![]() is the state X at site (i, j) and time t, and f is the transition rule.
is the state X at site (i, j) and time t, and f is the transition rule.
The state of each cell has three control variables: the grain orientation that represents the different grains and grain boundary energy; the state variable that indicates the state of the cell; and the dislocation density that represents the site dislocation energy. For simplifying the model, two assumptions are proposed in this work.
(1) The dislocation density of primary grain is uniform and identical, and the initial dislocation density of the newly formed DRX is set as zero.
(2) The nucleation of DRX only occurs at the grain boundary and the second phase particles distribute in the alloy uniformly.
3 Model of cellular automaton
3.1 Model of dislocation density
In general, the accepted K-M model is used to predict the variation of dislocation density with strain, which is based on the assumption that the kinetic process of the plastic flow is determined by a single structural parameter (dislocation density). The flow stress is proportional to the square root of dislocation density, which can be written as
![]() (2)
(2)
where σ is the flow stress, α is the dislocation interaction term, b is the Burger’s constant, μ is the shear modulus, and ρ is the dislocation density.
Two factors influence the dislocation density during hot deformation: the work hardening and the dynamic recovery (softening). The dislocation density with respect to strain can be expressed as [11]
![]() (3)
(3)
where ε is the strain, k1 (k1=2θ/(αμb)) is the constant that represents work hardening, k2 (k2=2θ0/σp) is the softening parameter that represents recovery of dislocations [12], σp is the peak stress, and θ0=dσ/dε is the hardening rate that can be obtained from the slope of the experimental flow stress—strain curve [13].
According to K—M model, it is assumed that θ0 is a function of deformation strain rate and temperature, which can be expressed as follows:
![]() (4)
(4)
where A1, B1, and C1 are the constants, ![]() is strain rate, and T is the temperature.
is strain rate, and T is the temperature.
From Eqn.(4) we can obtain:
![]() (5)
(5)
According to the isothermal compress tests [13-14], constants A1, B1 and C1 can be determined by one-dimensional linear regression analysis (see Figs.1 and 2). All correlation coefficients for these linear regressions are above 0.96. So Eqn.(4) can be written as:
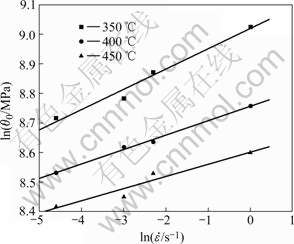
Fig.1 Relationship between ln θ0 and ![]()
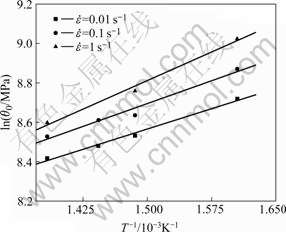
Fig.2 Relationship between ln θ0 and 1/T
![]() (6)
(6)
Fig.3 shows the comparison between the predicted values of θ0 and the experimental results. Obviously, the predicted values agree well with experimental results.
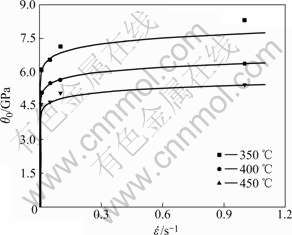
Fig.3 Comparison between predicted and experimental results
Substituting Eqn.(6) into Eqn.(3), the dislocation density can be expressed as
![]()
![]() (7)
(7)
Obviously, Eqn.(7) can predict the dislocation density in process with varying strain rate and temperature.
3.2 Model of DRX nucleation
XU and JIANG [15] and RICHERT and STUWE [16] proposed a theoretical model based on the dislocation density and assumed that the R-grains started to nuclear with a certain rate ![]() when the dislocation density reached the critical value ρc. Then the R-grains grow and decrease the dislocation density in the deformed materials.
when the dislocation density reached the critical value ρc. Then the R-grains grow and decrease the dislocation density in the deformed materials.
It was thought that the nucleation rate had the relationship not only with the strain rate, but also with the temperature and active energy [8]:
![]() (8)
(8)
where C is the constant related to material, Qact is the active energy, and R is the mole gas constant.
The active energy Qact can be obtained in the experiment. A generally accepted hyperbolic sine function that expresses the flow stress is given as [17]
![]() A[sinh(ασp)]nexp[-Qact/(RT)] (9)
A[sinh(ασp)]nexp[-Qact/(RT)] (9)
where A, α, and n are the material constants.
When strain rate is a constant, Qact can be calculated from Eqn.(9) [13-14]:
![]() (10)
(10)
3.3 Model of DRX growth
The growth of R-grains is a process of grain boundary migration in grains. It is generally accepted that the driving force for the growth of R-grains comes from the stored strain energy difference between the R-grains and the matrix. The growth velocity (vi) is proportional to the driving force (pi) per unit area:
vi=Mpi (11)
where M is the grain boundary mobility:
![]() (12)
(12)
where k is the Boltzmann constant, D0 is the boundary self-diffusion coefficient, and Qb is the boundary diffusion activation energy.
The change of free energy for R-grains comes from the decrease in the deformation storage energy and the increase in the boundary energy. The driving force of the ith R-grains can be calculated by
![]() (13)
(13)
where G is the free energy and V is the volume for R-grains. τ is the dislocation line energy represented by
τ=0.5μb2 (14)
γi is the boundary energy calculated by
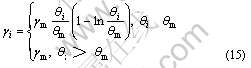
where θi is the misorientation between the ith R-grain and its neighbourhood grain, and θm, and γm are critical misorientation and boundary energy when the grain boundary becomes the large-angle boundary, respectively.
4 Results and discussion
The grain growth of aluminium alloy 7050 material under different deformation conditions were simulated by CA algorithm mentioned above. The material parameters needed in simulation are shown in Table 1.
Table 1 Materials parameters for 7050 aluminium alloy

The simulation area corresponds to a real region of 0.4 mm×0.4 mm, which was represented by a simulation mesh with 500×500 square lattice. According to experimental results, the mean diameter of the initial grain size in the simulation was set as 100 μm. The orientation of each primary grain was randomly set as an angle in the range of 0-180?.
To analyze the microstructure evolution for aluminium alloy 7050, the CA program was employed to simulate the nucleation and grain growth under different deformation conditions. Under the conditions of a temperature of 450 ?C and a strain of 5, the grain growth increases with the decrease of the strain rate, as shown in Fig.4. The grey regions denote the R-grains and the white regions denote the deformed matrix. At a strain rate of 1 s-1, no nucleation occurs. This is because there is no sufficient time for the growth of DRX in the period of grain growth. With the decrease of the strain rare, the nucleation appears at the grain boundary and the DRX begins to grow. Furthermore, the growing and migrating grains occupy the whole square area as the strain rate decreases to 0.01 s-1. Obviously, the strain rate is an important factor that affects the nucleation and growth of R-grains.

Fig.4 CA simulation results of influence of strain rate on DRX for aluminium alloy 7050 during hot deformation at temperature of 450 ?C and strain of 5: (a) ![]() 1 s-1; (b)
1 s-1; (b) ![]() 0.1 s-1; (c)
0.1 s-1; (c) ![]() 0.05 s-1; (d)
0.05 s-1; (d) ![]() 0.01 s-1
0.01 s-1
The influence of the deformation temperature on the microstructure evolution for this material is shown in Fig.5. When the temperature increases from 350 to 450℃, the percentage of DRX increases greatly and the mean grain decreases from 50.0 to 39.3 μm. It should be noted that the temperature had the double effects on the grain size. On one side, the temperature provides the essential active energy for the nucleation and the growth of DRX. On the other side, higher temperature may lead to larger grain size. At 350 ℃, the nucleation of DRX starts at the grain boundary, which has a minor effect on the grain size. As the temperature reaches 400 ℃, the DRX begins to grow and refine the grain. So, the desired deformation temperatures for aluminium alloy 7050 are from 400 to 450 ℃.

Fig.5 CA simulation results of influence of temperature on DRX of aluminium alloy 7050 during hot deformation at strain rate of 0.01 s-1 and strain of 5: (a) 350 ℃; (b) 400 ℃; (c) 420 ℃; (d) 450 ℃
The effects of deformation parameters on DRX percentage are shown in Fig.6. It is clear from the figure that the percentage of DRX depends on three factors: strain, strain rate and temperature. During hot deformation, higher strain, lower strain rate and higher temperature are helpful for enhancing the percentage of DRX.
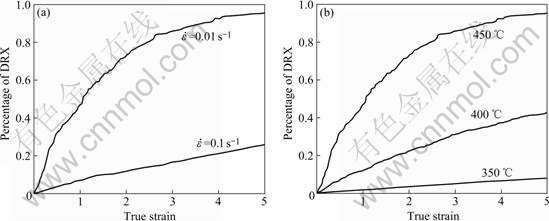
Fig.6 Influence of stain rate and temperature on percentage of DRX of aluminium alloy 7050: (a) t=450 ℃; (b) ![]() 0.01 s-1
0.01 s-1
Fig.7 shows the effect of strain, temperature and strain rate on the mean grain size of aluminium alloy 7050. It can be seen clearly from the figure that the mean grain size decreases with increasing the strain, which is characterized by the abrupt slope at the beginning of deformation and the stabilization at the stage of sufficient DRX. At a given temperature of 450 ℃, the mean grain size is smaller at a strain rate 0.01 s-1 than that at a strain rate 0.1 s-1 (see Fig.7(a)). At a given strain rate of 0.01 s-1, the mean grain size decreases with the increase of the temperature (see Fig.7(b)).
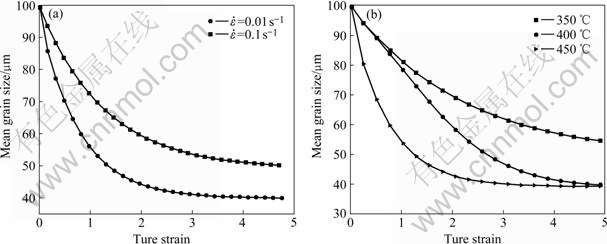
Fig.7 Influence of strain rate and deformation temperature on mean grain size of aluminium alloy 7050: (a) t=450 ℃; (b) ![]() 0.01 s-1
0.01 s-1
The mean size of R-grains that are important to describe DRX, was analyzed at different strain rates and temperatures, as shown in Fig.8. It is clear from this figure that the mean size of R-grain changes greatly with the strain rate and temperature, but, the strain has few effects on the mean size of R-grains. This means that the R-grains size depends on the Zener-Hollomon parameter [18-19]:
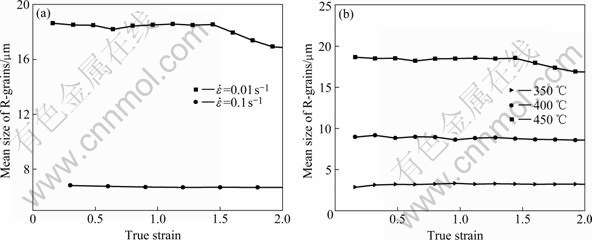
Fig.8 Influence of strain rate and deformation temperature on mean size of R-grains: (a) t=450 ℃; (b) ![]() 0.01 s-1
0.01 s-1
5 Conclusions
(1) A unified quantitative model coupling the CA method and the metallurgical principles of DRX is developed to simulate the microstructure evolution. The approach provides a multi-scale modelling to bridge macroscopic deformation parameters to microscopic DRX activities. The material constants in the models are determined by the isothermal compression tests on Gleeble 1500 machine.
(2) The influence of deformation parameters on the DRX of aluminium alloy 7050 is discussed. A high strain above 5 is needed for sufficient DRX, and the mean size of R-grains is mainly determined by the Zener-Hollomon parameters.
(3) During hot deformation, higher strain, lower strain rate and higher temperature are helpful for enhancing the percentage of DRX. As the temperature increases from 350 to 450 ℃ at a strain rate of 0.01 s-1, the percentage of DRX increases greatly and the mean grain size decreases from 50.0 to 39.3 μm. The desired deformation temperature is from 400 to 450 ℃.
(4) The established model can simulate the microstructure evolution successfully. However, the model cannot be applied to industrial production. So, the CA model coupling FEM with grain deformation is established to predict the microstructure of every position in work piece.
References
[1] KUGLER G, TURK P. Modeling the dynamic recrystallization under multi-stage hot deformation [J]. Acta Materialia, 2004, 51(15): 4659-4668.
[2] LAN Y J, LI D Z. Mesoscale simulation of ferrite transformation form deformed austenite during continuous cooling in a C-Mn steel using a cellular automaton method [J]. Acta Materialia, 2005, 53(4): 991-1003.
[3] GOETZ R L, SEETHARAMAN V. Modeling dynamic recrystallization using cellular automata [J]. Scripta Materialia, 1998, 38(6): 405-413.
[4] ZHANG Jun-hong, HUANG Bai-yun, HE Yue-hui, ZHOU Ke-chao, MENG Li-ping. Physical simulation of hot deformation of TiAl based alloy [J]. Journal of Central South University of Technology, 2002, 9(2): 73-76.
[5] ROLLETT A D, LUTON M J, SROLOVIZE D J. Microstructure simulation of dynamic recrystallization [J]. Acta Metall Mater, 1992, 40(1): 43-55.
[6] PEZAK P, LUTON M J. A monte carlo study of the influence of dynamic recovery on dynamic recrystallization [J]. Acta Metal Mater, 1993, 41(1): 59-71.
[7] PEZAK P. A monte carlo study of influence of deformation temperature on dynamic recrystallization [J]. Acta Metall Mater, 1995, 43(3): 1279-1291.
[8] DING R, GUO Z X. Coupled quantitative simulation of microstructural evolution and plastic flow during dynamic recrystallization [J]. Acta Materialia, 2001, 49(16): 3163-3175.
[9] XIAO Hong, XU Yu-chen, YAN Yan-hong. Cellular automaton method for simulation of dynamic recrystallization process with consideration of grains deformation [J]. China Mechanical Engineering, 2005, 16(24): 2245-2249. (in Chinese)
[10] JIN Wen-zhong, WANG Lei, LIU Xiang-hua. Modeling of cellular automaton method in the simulation of recrystallization [J]. Materials for Mechanical Engineering, 2005, 29(10): 10-13. (in Chinese)
[11] ESTRIN Y. Unified constitutive laws of plastic deformation [M]. London: Academic Press, 1996.
[12] XIAO Na-min, ZHENG Cheng-wu. A simulation of dynamic recrystallization by coupling a cellular automaton method with a topology deformation technique [J]. Computational Materials Science, 2008, 41(3): 366-374.
[13] YI You-ping, YANG Ji-hui, LIN Yong-cheng. Flow stress constitutive equation of 7050 aluminium alloy during hot compression [J]. Journal of Materials Engineering, 2007(4): 20-22. (in Chinese)
[14] YI You-ping, FU Xin, CUI Jin-dong, CHEN Hua. Prediction of grain size for large-sized aluminium alloy 7050 forging during hot forming [J]. Journal of Central South University of Technology, 2008, 15(1): 1-5.
[15] XU Nin-gan, JIANG Hui. TEM and HRTEM study of influence of thermal cycles with stress on dynamic recrystallization in Ti46Al8Nb1B during creep [J]. Micron, 2008, 39(8): 1210-1215.
[16] RICHERT M, STUWE H P. Work hardening and microstructure of AlMg5 after severe plastic deformation by cyclic extrusion and compression [J]. Materials Science and Engineering,2003, 335(2): 180-185.
[17] CHEN Hui-qin, CAO Chun-xiao. Hot deformation mechanism and microstructure evolution of TC11 titanium alloy in β field [J]. Transactions of Nonferrous Metals Society of China, 2008, 18(5): 1021-1027.
[18] DERBY B. The dependence of grain size on stress during dynamic recrystallization [J]. Acta Metal Mater, 1991, 39(5): 955-962.
[19] DERBY B. Dynamic recrystallization: the steady state grain size [J]. Scripta Metal Mater, 1992, 27(11): 1581-1585.
Foundation item: Project(2005CB724105) supported by the Major State Basic Research Program of China; Project(IRT0549) supported by Program for Changjiang Scholars and Innovative Research Team in University
Received date: 2008-07-25; Accepted date: 2008-09-30
Corresponding author: YI You-ping, Professor, PhD; Tel: +86-13319599319; E-mail: yyp@mail.csu.edu.cn
- Simulation of dynamic recrystallization for aluminium alloy 7050 using cellular automaton


