四辊轧机辊系的横向自由振动
孙建亮1，彭 艳1，刘宏民1，江光彪2
(1. 轧制设备及成套技术教育部工程研究中心，亚稳材料制备技术与科学国家重点实验室，
燕山大学，河北 秦皇岛，066004；
2. 宝山钢铁集团有限公司，上海，200941)
摘 要：
摘 要：为研究轧机辊系沿辊身长度方向的振动特性及其对板带材板形质量的影响，以四辊轧机为研究对象，将工作辊和支撑辊看作弹性连续体，辊间接触认为是Winkler弹性基础，建立轧机辊系的横向振动模型。根据 欧拉-伯努力梁理论，采用模态叠加法对轧机辊系自由振动耦合方程进行求解，得到四辊轧机辊系横向振动的自然频率、主振型和振动方程。对宝钢2030冷轧机组进行数值模拟，分析其辊系横向振动特性。研究结果表明：四辊轧机辊系横向振动包括2个无限序列的自然频率ω1n和ω2n；辊系横向自由振动由2种振动模式组成，即低频的同步振动和高频的异步振动；辊系横向振动中模式
起主要作用，低阶时工作辊的振动比支承辊的振动剧烈；高阶时支承辊振幅大于工作辊振幅，奇数阶振幅大于偶数阶振幅；轧辊横向振动对带材板形质量有重要影响。
关键词：
中图分类号：TG333 文献标识码：A 文章编号：1672-7207(2009)02-0429-07
Free transverse vibration of rolls for four-high mill
SUN Jian-liang1, PENG Yan1, LIU Hong-min1, JIANG Guang-biao2
(1. Engineering Research Center of Rolling Equipment and Complete Technology of Ministry of Education,
State Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao 066004, China;
2 Hot Rolling Mill of Baoshan Iron and Steel Co. Ltd., Shanghai 200941, China)
Abstract: In order to study the transverse vibration of rolls for four-high mill and its effect on the strip shape, the free transverse vibration model of rolls for four-high mill was built. The work roll and backup roll were considered as elastic continuous bodies and the work roll and backup roll were joined by a Winkler elastic layer. According to Euler-Bernoulli beam theory, the coupled equations of free transverse vibration of rolls were solved based on modal superposition method. The numerical modeling was made on 2030 cold tandem mill of Baoshan Iron and Steel Company. The free transverse vibration characteristics of rolls were analyzed, and the natural frequency, principal mode and motion equations were determined. The results show that the free transverse vibration of rolls includes two kinds of vibration modes which are the synchronous vibration at low frequencies ω1n and the asynchronous vibration at high frequencies ω2n. The sequence n=1 plays more important role in the free transverse vibration of rolls. The vibration amplitude of work roll is bigger than that of the backup roll in low order, and it is reverse in high order. The vibration amplitude of odd-order is bigger than that of the even-order. The transverse vibration of rolls for four-high mill has important effect on the strip shape.
Key words: four-high mill; free transverse vibration of rolls; modal superposition method
随着国民经济的发展，人们对板带材质量尤其是板形质量要求越来越高。轧机垂直振动对轧机本身和板带材质量有重大影响，许多研究者对轧机垂直振动进行了研究[1-4]，如Hu等[5-6]建立了单自由度和多自由度轧机振动模型，研究了轧机系统的稳定性，对连轧过程进行了仿真；邹家祥等[7]针对宝钢2030冷连轧机振动问题进行分析，将该轧机简化为六自由度不对称“质量弹簧系统”，分析了宝钢2030冷轧机的震颤问题；陈勇辉等[8-9]考虑轧机系统的非线性刚度和阻尼特性，建立了一种四辊冷带轧机二自由度非线性参激振动模型，用数值方法研究了其稳定性。段吉安等[10]研究了轧制过程工作界面的动力学特性，分析了金属塑性流动、界面摩擦学、工作辊振动的行为机理和其耦合特性。这些研究大多是将轧辊简化为集中质量，采用集中质量法进行研究，很好地解决了振动使板带材产生的厚度误差和表面振纹等问题。然而，轧辊是一弹性连续体[11-12]，而且目前轧机的发展趋势为大型宽带轧机，轧件宽度较大，轧辊辊身长度较大，在这种情况下，认为轧辊是一质点，忽略辊身长度方向的信息，对于研究辊系的振动和由此引起的板带材宽度方向的板形质量问题是不充分的[13]。为此，本文作者将轧机辊系看作弹性连续体，以四辊轧机辊系为研究对象，采用欧拉-伯努利梁理论，建立四辊轧机辊系横向自由振动模型[14-15]。对宝钢2030冷轧机组进行数值模拟，分析轧机辊系的横向自由振动特性，求得其自然频率和主振型，分析振动影响因素。
1 轧机辊系结构模型
四辊轧机的辊系物理模型如图1所示。工作辊受到轧制压力作用，工作辊和支承辊受到弯辊力作用。为了研究轧机辊系横向振动，假设轧辊是各向同性的等截面梁，假设辊间接触为Winkler弹性基础，弹性系数为K；工作辊和支承辊是简支梁[14-15]。不考虑剪切变形和转动惯量对轧辊横向振动的影响，应用欧 拉-伯努利梁理论对轧辊的横向振动进行分析，其力学模型如图2所示。由图2可知，工作辊和支承辊通过弹性基础耦合在一起，二者的振动特性相互影响。为了分析过程的通用性，假设工作辊和支承辊两端受到弯辊力作用，工作辊和支承辊受到任意分布压力作用(在真实情况下，支承辊不受分布压力作用)。
图1 四辊轧机辊系物理模型
Fig.1 Physical model of rolls for four-high mill
图2 四辊轧机辊系简化为弹性基础梁模型
Fig.2 Simplified mechanical model of rolls for four-high mill
根据所建力学模型，建立轧辊横向振动方程：
；
。(1)
为便于计算，令
，
，
，
(i为b或w)，则有：
；
。 (2)
将工作辊和支承辊都简化为弹性基础上的简支梁，其边界条件和初始条件如下：
。 (3)
，
(i为b或w)。 (4)
其中：zb(y, t)和zw(y, t)分别为支承辊和工作辊的振动方程；fb(y, t)和fw(y, t)分别为支承辊和工作辊受到的任意分布力；Eb和Ew分别为支承辊和工作辊的弹性模量；Ib和Iw为支承辊和工作辊的截面惯性矩；ρb和ρw为支承辊和工作辊的材料密度；Ab和Aw为支承辊和工作辊的横截面面积。
2 辊系自由振动数学模型
要分析辊系的受迫振动，首先分析辊系的自由振动，求解辊系的自然频率和相应的振型。辊系自由振动的力学模型如图3所示。辊系的自由振动方程如下：
；
。 (5)
图3 四辊轧机辊系横向自由振动模型
Fig.3 Free transverse vibration model of rolls for four-high mill
设微分方程(5)在边界条件下的解为：
；
i为b或w； (6)
。 (7)
其中：
(n=1, 2, 3, …)；xn(y)为已知的振型函数；Tbn(t)和Twn(t)为未知的时间函数；L为辊身长度。
将式(6)代入式(5)，有：
；
。 (8)
于是，从(8)式可得：
；
。 (9)
其中：
；
；
；i为b或w。
方程(9)的解为：
，
，
。
其中：ωn为系统自然频率；Cn和Dn为未知常数。
将该解代入方程(9)中，有：
；
。 (10)
要使方程组有解，则其系数行列式为零：
。
即 
。 (11)
方程(11)的解为：
，
ω1n＜ω2n 。 (12)
因此，方程(9)的解可以写作以下形式：
；
。
通过三角变换，上式的等价形式为：
；
。 (13)
将式(13)代入式(9)，可得系数ain：
。 (14)
将式(12)代入式(14)，系数ain可变形为：
，
a1n＞0，a2n＜0。 (15)
最后，得到轧辊自由振动方程：
。(16)
。(17)
其中：
，
；Xbin和Xwin分别为辊系在自然频率ωin下的振型。
根据初始条件求解未知参数Ain和Bin，模态函数的正交性为：
。
其中：
为克罗内克符号，
；
。
将初始条件代入振动方程(17)，根据模态函数的正交性，可得：
；
；
；
。
联解上面各式可得：
；
；
；
。
假设初始条件为：
，
，
。
则：
；
；
。
因此，轧辊自由振动方程为：
由轧辊横向自由振动方程可知，四辊轧机辊系横向振动包括2个无限序列的自然频率ω1n和ω2n，且 ω1n＜ω2n。根据系数a1n＞0和a2n＜0可知，辊系由2种振动模式组成：低频ω1n的同步振动和高频ω2n的异步振动，两者分别对应于a1n＞0和a2n＜0。图4给出了不同模式下n=1, 2, 3, …时辊系的振型图，这里取n=1和2为例进行说明。
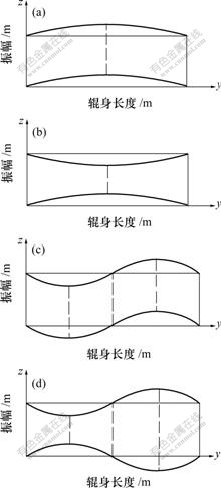
(a) i=1, n=1, a11＞0, ω11, k1=π/L; (b) i=2, n=1, a21＞0, ω21, k1=π/L; (c) i=1, n=2, a12＞0, ω12, k2=2π/L; (d) i=2, n=2, a22＞0, ω22, k2=2π/L
图4 前2阶轧机辊系振型图
Fig.4 Mode shapes of vibration of rolls corresponding to the first two pairs of natural frequencies
3 数值模拟
3.1 数值模拟参数
以宝钢2030冷连轧机组为研究对象进行数值模拟。该冷轧机组由5机架四辊冷轧机、开卷机、卷取机和其他辅助设备组成。冷轧机的主要参数如下[8]：工作辊直径为550~615 mm；工作辊辊身长度为2.03 m；支承辊直径为1.425~1.550 m；支承辊辊身长度为 2.03 m；弹性模量Eb=Ew=2.1×1011 Pa；密度ρb=ρw= 7.8×103 kg/m3；基弹性刚度K=6×1010 N/m。
本文取工作辊和支承辊最大直径进行仿真计算，即Db=1.550 m，Dw=0.615 m。
3.2 仿真分析
取初始条件为：
，
，
。基于上述参数，采用Matlab编程进行数值模拟，辊系自然频率ω1,n和ω 2n以及振型系数a1n和a2n的计算结果见表1和表2。其中：ω1n和ω2n分别为第1阶和第2阶振动固有频率；a1n和a2n分别为ω1n和ω2n对应的系数。
表1 四辊轧机辊系横向振动自然频率
Table 1 Natural frequencies of rolls for four-high mill
表2 四辊轧机辊系横向振动振型系数
Table 2 Coefficients of natural mode shapes
图5和图6所示是模式n=1时工作辊和支撑辊自由振动随时间变化的三维图。可见，轧辊的一阶主振型呈二次曲线，轧辊中部振动比轧辊边部剧烈，并且随时间呈周期性变化。工作辊和支承辊的振幅很大，工作辊的振动幅度大于支承辊振动幅度，工作辊振动较剧烈。工作辊与板带材直接接触，是板带材产品的加工工具，其工作状态直接影响板带产品质量。
图5 n=1时支承辊自由振动三维图
Fig.5 Free transverse vibration of backup roll at n=1
图6 n=1时工作辊自由振动三维图
Fig.6 Free transverse vibration of work roll at n=1
图7~10所示是模式n为2和3时支撑辊和工作辊的横向振动随时间变化的三维图像。可以看出，工作辊与支承辊的振动方向相反。高阶时支承辊振幅大于工作辊振幅，奇数阶振幅大于偶数阶振幅。
图7 n=2时支承辊自由振动三维图
Fig.7 Free transverse vibration of backup roll at n=2
图8 n=2时工作辊自由振动三维图
Fig.8 Free transverse vibration of work roll at n=2
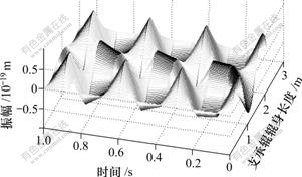
图9 n=3时支承辊自由振动三维图
Fig.9 Free transverse vibration of backup roll at n=3
图10 n=3时工作辊自由振动三维图
Fig.10 Free transverse vibration of work roll at n=3
比较图7~10可知，模式n=1时轧辊振幅大，对工作辊和支撑辊横向振动起主要作用。当n为2和3时，工作辊和支承辊的振幅很小，但其振动形式确实存在。由于轧机长时间在恶劣的环境下连续工作，即使轧辊振幅很小，但由于其长期反复振动，必然导致轧辊磨损，降低轧辊的表面质量、寿命和强度。
4 结 论
a. 基于欧拉-伯努利梁理论，采用模态叠加法建立了四辊轧机辊系的横向自由振动模型，求解了工作辊和支承辊的耦合运动方程，对辊系横向振动特性进行研究，得到辊系横向自由振动的自然频率、主振型和辊系的横向自由振动方程。
b. 四辊轧机辊系横向振动包括2个无限序列的自然频率ω1n和ω2n，且ω1n＜ω2n。由系数a1n＞0和a2n＜0可知，辊系由2种振动模式组成：低频ω1n的同步振动和高频ω2n的异步振动，两者分别对应于 a1n＞0和a2n＜0。
c. 对宝钢2030冷轧机组进行了数值模拟，求解了它的固有频率和振型方程，得到了不同模式下辊系的三维振型图。辊系横向振动中模式n=1起主要作用，工作辊的振动比支撑辊剧烈，高阶时支承辊振幅大于工作辊振幅，奇数阶振幅大于偶数阶振幅。虽然高阶时轧辊振幅很小，但其振动形式确实存在，必然导致轧辊磨损，降低轧辊寿命和板带材质量。因此，对辊系横向振动进行研究，进一步分析其对板形质量的影响有重要意义。
参考文献：
[1] Yun I S, Wilson W R D, Ehmann K F. Chatter in the strip rolling process. Part Ⅰ: Dynamic model of rolling[J]. Transactions of the ASME: Journal of Manufacturing Science and Engineering, 1998, 120(2): 330-336.
[2] Yun I S, Wilson W R D, Ehmann K F. Chatter in the strip rolling process. Part Ⅰ: Dynamic rolling experiments[J]. Transactions of the ASME: Journal of Manufacturing Science and Engineering, 1998, 120(2): 337-342.
[3] Yun I S, Wilson W R D, Ehmann K F. Chatter in the strip rolling process. Part Ⅲ: Chatter model[J]. Transactions of the ASME: Journal of Manufacturing Science and Engineering, 1998, 120(2): 343-348.
[4] TANG Hua-ping, DING Rui, WU Yun-xin, et al. Investigation for parametric vibration of rolling mill[J]. Trans Nonferrous Met Soc China, 2002, 12(3): 485-488.
[5] Hu P H, Ehmann K F. A dynamic model of the rolling process: PartⅠ[J]. Int J Mach Tools Manuf, 2000, 40(1): 1-19.
[6] Hu P H, Ehmann K F. A dynamic model of the rolling process: Part Ⅱ[J]. Int J Mach Tools Manuf, 2000, 40(1): 21-31.
[7] 邹家祥, 徐乐江. 冷连轧机系统振动控制[M]. 北京: 冶金工业出版社, 1998: 107-136.
ZOU Jia-xiang, XU Le-jiang. The vibration control of cold tandem rolling mill[M]. Beijing: Metallurgical Industry Press, 1998: 107-136.
[8] 陈勇辉, 刘世元, 廖广兰. 四辊冷轧机三倍频振颤机理的研究[J]. 机械工程学报, 2003, 39(6): 118-123.
CHEN Yong-hui, LIU Shi-yuan, LIAO Guang-lan. Study on third octave mode chatter on 4-h cold rolling mills[J]. Chinese Journal of Mechanical Engineering, 2003, 39(6): 118-123.
[9] 陈勇辉, 史铁林, 杨叔子. 四辊冷轧机非线性参激振动的研究[J]. 机械工程学报, 2003, 39(4): 56-60.
CHEN Yong-hui, SHI Tie-lin, YANG Shu-zi. Study on parametrically excited nonlinear vibrations on 4-h cold rolling mills[J]. Chinese Journal of Mechanical Engineering, 2003, 39(4): 56-60.
[10] 段吉安, 钟 掘. 高速轧机工作界面的负阻尼特性[J]. 中南工业大学学报: 自然科学版, 2002, 33(2): 401-404.
DUAN Ji-an, ZHONG Jue. Negative damping of rolling interface for rolling chatter[J]. Journal of Central South University of Technology: Natural Science, 2002, 33(2): 401-404.
[11] Oniszczuk Z. Free transverse vibration of an elastically connected complex simply supported double-beam system[J]. Journal of Sound and Vibration, 2003, 232(2): 387-403.
[12] Oniszczuk Z. Forced transverse vibration of an elastically connected complex simply supported double-beam system[J]. Journal of Sound and Vibration.2003, 264(2): 273-286.
[13] PENG Yan, LIU Hong-min, WANG Dong-cheng. Simulation of type selection for 6-high cold tandem mill based on shape control ability[J]. Journal of Central South University of Technology, 2007, 14(2): 278-284.
[14] Zhang Y Q, Lu Y, Ma G W. Effect of compressive axial load on forced transverse vibration of a double beam system[J]. Internal Journal of Mechanical Sciences, 2007, 50(2): 299-305.
[15] De Rosa M A, Lippiello M. Non-classical boundary conditions and DQM for double-beams[J]. Mechanics Research Communications, 2007(34): 538-554.
收稿日期：2008-04-22；修回日期：2008-07-02
基金项目：国家自然科学基金资助项目(50875231)；河北省重大自然科学基金资助项目(E2006001038)
通信作者：孙建亮(1981-)，男，河北永清人，博士研究生，从事板带轧机动态建模及板形板厚综合动态控制研究；电话：0335-8067916；E-mail: sunjl_1981@163.com
