
J. Cent. South Univ. (2019) 26: 1696-1705
DOI: https://doi.org/10.1007/s11771-019-4126-3
Upper bound solution of surrounding rock pressure of shallow tunnel under nonlinear failure criterion
ZHANG Dao-bing(张道兵), MA Zong-yu(马宗宇), YU Biao(蔚彪), YIN Hua-dong(尹华东)
Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract:
The nonlinear Baker failure criterion is introduced into the upper-bound limit analysis to examine the face stability of a shallow tunnel. The tunnel face under the ultimate limit state is analyzed from the perspective of energy balance. The work rates of external forces and internal energy dissipation are calculated. An analytical solution of necessary face pressures is derived. The optimal upper-bound solution of the face pressures is obtained by optimization. The results show that the three dimensionless parameters A, T, n of nonlinear Baker failure criterion have different effects on the necessary face pressures and the pattern failure mechanisms ahead of tunnel face. A is the most important one; n takes the second place, and T is the least one. The computed necessary face pressures are nonlinearly increasing when A is reduced. Combined with the actual monitoring data of Taxia tunnel, the calculation results in this paper is verified. It is suggested that the tunnel face supports should be strengthened timely in soft rocks to prevent the occurrence of face collapse.
Key words:
Cite this article as:
ZHANG Dao-bing, MA Zong-yu, YU Biao, YIN Hua-dong. Upper bound solution of surrounding rock pressure of shallow tunnel under nonlinear failure criterion [J]. Journal of Central South University, 2019, 26(7): 1696-1705.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-019-4126-31 Introduction
In tunnel excavations, the initial stress balance is disturbed in rocks and soils. Stress adjustment leads to stress concentrations around the tunnel face. It is very easy to cause great surface settlements and even face collapse. Therefore, to determine necessary face pressures has become a key problem in the analysis of tunnel face stability. The research of tunnel face stability has important theoretical value and engineering significance.
At present, the research methods of tunnel face stability mainly include limit equilibrium method, slip line method, model test, numerical simulation, limit analysis method and so on [1-5]. Compared with other methods, the calculation process of limit analysis is simple, fast, and the calculation results are more accurate. Therefore, it is widely used in the analysis of tunnel stability problems in recent years. Sloving the pressure of surrounding rock based on nonlinear criterion and limit analysis method has been applied by many scholars. ABID et al [6] investigated the influence of spatial variability on the undrained stability of an unlined circular tunnel using adaptive random finite element limit analysis. DANIEL et al [7] studied the stability of a square tunnel in undrained clay with a rigid block mechanism by means of limit analysis finite element method.KENTARO et al [8] solved the stability of dual circular tunnels in clay under overload loads. The center distance of dual circular tunnel was taken as a new parameter, and the ultimate additional load was obtained by the limit analysis method. XU et al [9] derived the expressions of required reinforcement strength and the stability factor under different distribution patterns within the framework of limit analysis and the generalized tangent technique from the energy balance equations. SALVADOR et al [10] structured a recent rotational face collapse mechanism based on upper-bound limit analysis, which can predict the critical face pressures and the type of collapse.
The upper bound theorem of limit analysis was adopted by NIMA et al [11] to calculate the face pressures with linear variations of cohesions. The factor of safety against the tunnel face instability was also calculated using the strength reduction technique and the upper bound theorem. GUAN et al [12] studied the effect of many factors on the collapse pressures of underground chambers with the limit analysis upper bound theorem. LI et al [13] used limit analysis to study the stability of cracks and water pressure on soil-wall system. LI et al [14] used kinematics theorem of limit analysis and Newmark method to analyze seismic displacement of rock slope. The results of calculations were given for a series of actual seismic waves and compared with the results calculated from empirical formula. XU et al [15] considered the combined effect of soil strength nonlinearity and shear dilatancy, the seismic stability of three-dimensional secondary slope was analyzed. Based on the limit analysis method, the external loading rate, seismic force and internal energy dissipation of the slope were calculated, and then the critical height of the slope was deduced. PAN et al [16] estimated the safety factor of a tunnel face with a non-circular section using the upper-bound theorem in combination with the strength reduction technique, in which the effect of the cross-sectional shape on safety factors was discussed. PAN et al [17] investigated face stability of a circular tunnel in weak rock masses under a three-dimensional steady-state seepage flow based on the kinematical approach of limit analysis.
MEHDI et al [18] studied stress behavior of shallow tunnels under simultaneous non-uniform surface traction and symmetric gravity loading by using a boundary element method. LI et al [19] set up active and passive failure mechanisms based on limit analysis method, and put forward a probabilistic analysis method for the stability of metro tunnel face. JAGDISH et al [20] studied the stability of a long circular tunnel in a cohesive frictional soil medium in the presence of horizontal pseudo-static seismic forces. SEUNG et al [21] investigated the effects of tunnel diameters, cover-to-diameter ratios, lateral earth pressures coefficients, and soil strength parameters on the tunnel stability by means of three-dimensional finite element simulations. ZHANG et al [22] analyzed the face stability of a circular tunnel considering a series of tunnel diameter-to-depth ratios and soil properties by using three- dimensional numerical simulations. The limit support pressures on the tunnel face and the failure zone in front of the tunnel face were both obtained from the numerical simulations. YANG et al [23] developed a two-layer model and upper bound solutions for the shape of collapse block in rectangular tunnel subjected to seepage pressure with limit analysis theory and Hoek-Brown failure criterion, and then the reliability based analysis was performed.
The above study uses upper bound theorem of the limit analysis to study the stability of the tunnel incorporating the Mohr-Coulomb failure criterion or the Hoek-Brown failure criterion. However, Mohr-Coulomb failure criterion and Hoek-Brown failure criterion have some limitations. A large number of tests show that the material envelope of rock and soil is nonlinear [24]. The nonlinear failure criterion proposed by Baker is a generalized strength criterion for rock and soil mass. The conventional Mohr-Coulomb strength criterion, Griffith strength criterion and Hoek-Brown strength criterion are all its special cases. In order to expand the scope of this paper, the nonlinear Baker failure criterion is used with the limit analysis method to study the tunnel face stability.
2 Nonlinear Baker failure criterion and tangent line technique
Based on the results of the triaxial tests and previous experimental researches, a generalized rock strength criterion is proposed by BAKER [25]. The nonlinear strength criteria proposed by Baker are given as follows:
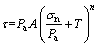 (1)
(1)
where τ represents shear stresses; Pa indicates atmospheric pressures; σn indicates normal stresses; A, n and T are related parameters which can be determined by experiments.
JIANG et al [26] reported that A is a scale parameter that affects the size of shear strength; n represents the order of failure criterion curves and affects the curvature of strength envelope, determined by the shear strength of rock masses. T is a transformation parameter and controls the intersection point between strength envelope and the σn axis. The ranges of A, n and T are: A>0, 1/2≤n≤1, T≥0, A, n and T can be determined through the triaxial tests of rock masses [27]. When n=1, A=tanφ, 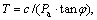 Eq. (1) is reduced to the Mohr-Coulomb strength criterion; when n=0.5,
Eq. (1) is reduced to the Mohr-Coulomb strength criterion; when n=0.5,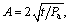 T=t/Pa, it is reduced to the Griffith strength criterion.
T=t/Pa, it is reduced to the Griffith strength criterion.
The tangential line method can be applied to the nonlinear Baker strength criterion [28], as shown in Figure 1.
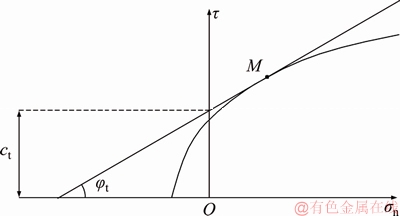
Figure 1 Strength curve of nonlinear Baker failure criterion
For any point M on the envelope, the expression of tangential line is given as follows:
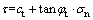 (2)
(2)
where ct and φt are the corresponding cohesion and internal friction angle at the M point, which can be determined by Eq. (3) and Eq. (4).
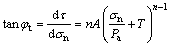 (3)
(3)
 (4)
(4)
Equation (4) shows the relation of several nonlinear parameters under the Baker strength criterion.
3 Upper limit theorem of limit analysis
The upper bound theorem requires that the internal energy dissipation is not less than the external power for a permissible failure mechanism, which can be expressed by following formula [29-32]:
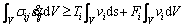 (5)
(5)
In Eq. (5), S and V are the surface area and the volume of the failure mechanism, respectively; Ti is the surface forces; Fi is the volume forces; σij is the stress field associated with Fi and Ti; vi is the allowable velocity field; 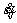 is a strain rate field compatible with vi. For tunnel face stability, by equating the work rate of external forces, including the gravity and face supporting pressures, to the internal energy dissipation, the necessary face pressures can be solved.
is a strain rate field compatible with vi. For tunnel face stability, by equating the work rate of external forces, including the gravity and face supporting pressures, to the internal energy dissipation, the necessary face pressures can be solved.
4 Construction of failure mode
A double logarithmic spiral failure mode used by MOLLON et al [33] and ZHANG et al [34] has been proved to be applicable to the shallow tunnel face stability. In this paper, the active failure mode of tunnel face constructed by the double logarithmic spirals is shown in Figure 2. C represents the depth of the tunnel, and D is the diameter of the tunnel.
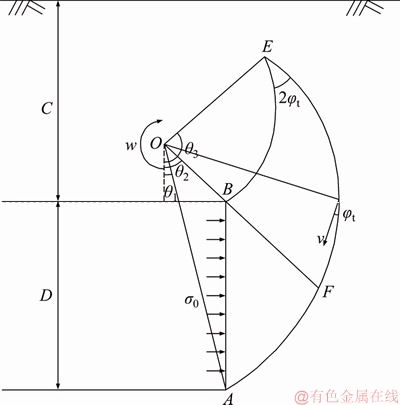
Figure 2 Failure mode of shallow tunnel face
AB is the face of tunnel. The failure mechanism is composed of two logarithmic spiral lines AE and BE; ra and rb represent the length of OA and OB, respectively. O is the rotational center and ω is the constant angular velocity. The two logarithmic spiral lines intersect at the point E. The angles of OA, OB, OE and vertical direction are θ1, θ2, θ3, respectively. The face support is taken as uniformly distributed loads, denoted by σ0.
The logarithmic spirals AE and BE are defined as follows:
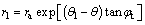 (6)
(6)
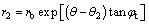 (7)
(7)
According to the geometric relation, the next formulas can be obtained.
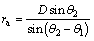 (8)
(8)
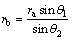 (9)
(9)
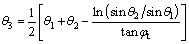 (10)
(10)
where ra and rb are functions of θ1 and θ2; θ3 is function of θ1 and θ2.
5 Calculation process
5.1 Work rate of gravity
In order to compute the work rate of the gravity, the failure mode is divided into two parts, BAF and BFE, respectively, as shown in Figure 2.
In the regional OAF, the external work rate of the gravity can be calculated with the following form:
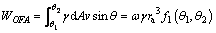 (11)
(11)
The expression of f1(θ1, θ2) is:
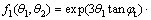
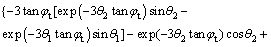
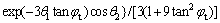 (12)
(12)
The work rate of gravity in the region OAB is expressed as:
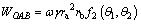 (13)
(13)
in which the expression of the function f2(θ1, θ2) is:
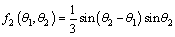 (14)
(14)
The work rate of the gravity of the region BAF is:
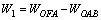 (15)
(15)
The gravity work rate in the region OBE is as follows:
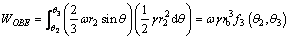 (16)
(16)
where the expression of f3(θ2, θ3) is:
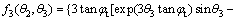
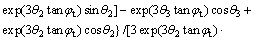
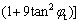 (17)
(17)
The work rate of gravity in the region OFE is as follows:
 (18)
(18)
where the expression of f4(θ2, θ3) is:
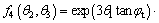
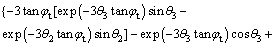
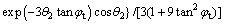 (19)
(19)
Thus, the work rate of gravity of the region BFE can be expressed as follows:
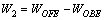 (20)
(20)
The work rate of the gravity of the whole failure mode is the sum of two parts of BAF and BFE:
 (21)
(21)
5.2 Work rate of face supporting pressures
The face supporting pressures σ0 can be simplified into uniformly distributed, and the velocities in front of the face at failure in different points are not the same. The corresponding work rate can be calculated by
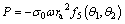 (22)
(22)
where the expression of f5(θ1, θ2) is as follows:
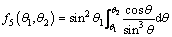 (23)
(23)
5.3 Internal energy dissipation
Internal energy loss occurs at two failure surface AE and BE. The internal energy loss on the failure surfaces BE and AE can be calculated by Eq. (24) and the Eq. (25), respectively.
 (24)
(24)
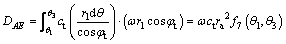 (25)
(25)
The expressions of f6(θ2, θ3) and f7(θ1, θ3) are expressed as:
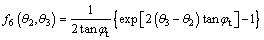 (26)
(26)
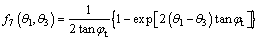 (27)
(27)
The total internal energy loss of the failure mode is computed by:
 (28)
(28)
5.4 Solving face supporting pressures
By equating the external work rate to the total internal energy dissipation, one obtains:
 (29)
(29)
Substituting Eqs. (21), (22) and Eq. (28) into Eq. (29) leads to the expression of the face supporting pressures as follows:
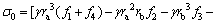
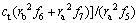 (30)
(30)
where f1-f7 are functions of θ1 and θ2, so the face pressure is also a function of θ1, θ2 and φt. The critical face pressure can be obtained by optimization with respect to θ1, θ2 and φt.
5.5 Determination of constraint conditions
In order to obtain the maximum value of the face pressures, the optimization should be done under certain constraints regarding to physical and geometric parameters. To sum up, the constraints can be determined as follows:
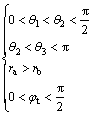 (31)
(31)
Combined with the upper bound theorem, the optimal solution is solved by the sequence two programming algorithm using the Matlab optimization tool.
6 Numerical simulation and comparisons
When n=1, A=tanφ,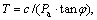 Eq. (1) is reduced to the Mohr-Coulomb strength criterion. In this paper, five groups of c and φ are obtained by n=1. According to this relation, the parameters A and T in the nonlinear Baker failure criterion are calculated. The values of face pressures are calculated for these two criteria. The numerical simulation of tunnel excavation is carried out by using Plaxis 3D. The results of Plaxis 3D were used as a reference item to compare the other two sets of data. The comparisons between the linear M-C criterion, the nonlinear Baker criterion and numerical simulations are shown in Table 1. It is seen that these two failure criteria give almost the same results. And the results of nonlinear Baker criterion are closer to the result of the Plaxis 3D. The comparison results verify the proposed method. It also shows that the linear Mohr-Coulomb failure criterion is a special case of the nonlinear Baker criterion.
Eq. (1) is reduced to the Mohr-Coulomb strength criterion. In this paper, five groups of c and φ are obtained by n=1. According to this relation, the parameters A and T in the nonlinear Baker failure criterion are calculated. The values of face pressures are calculated for these two criteria. The numerical simulation of tunnel excavation is carried out by using Plaxis 3D. The results of Plaxis 3D were used as a reference item to compare the other two sets of data. The comparisons between the linear M-C criterion, the nonlinear Baker criterion and numerical simulations are shown in Table 1. It is seen that these two failure criteria give almost the same results. And the results of nonlinear Baker criterion are closer to the result of the Plaxis 3D. The comparison results verify the proposed method. It also shows that the linear Mohr-Coulomb failure criterion is a special case of the nonlinear Baker criterion.
7 Parametric analysis and discussion
This paper mainly studies the effects of three parameters A, T, n of Baker failure criterion, depth ratio C/D, and the unit weight γ on tunnel face stability. In the calculations, the adopted parameters are: the unit weight γ=20-24 kN/m3, C/D=1.0-2.0. The dimensionless parameters are A=0.4-0.8. T=0.01-0.05. n=0.5-0.9. The results are shown in Figures 3-8.
Figure 3 studies the effect of C/D and γ on the necessary face pressures when C/D is 1.0-2.0, and the unit weight γ is 20, 21, 22, 23, 24 kN/m3, respectively. It can be seen from the diagram that for the same γ, the necessary face pressures σ0 almost does not change with C/D, and for a fixed C/D, the critical face pressures σ0 increases with the increase of γ.
Figures 4 and 5 shows the effect of A and n on the necessary face pressures when A changes from 0.4 to 0.8, n being 0.5, 0.6, 0.7, 0.8, 0.9 respectively. It can be seen that under the same n, the necessary face pressure σ0 decreases with the increase of A, and the necessary face pressure σ0 increases with the increase of n for the same A.
Table 1 Comparison results of linear M-C failure criterion, nonlinear Baker failure and numerical simulation
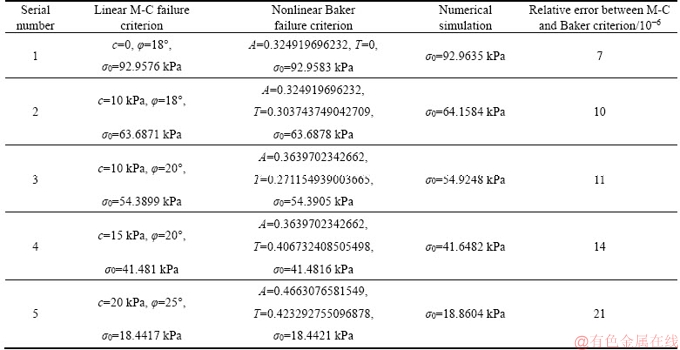
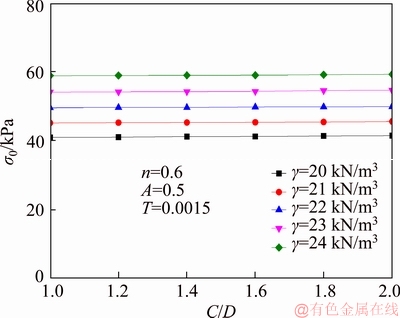
Figure 3 Influence of γ and C/D on face pressures σ0
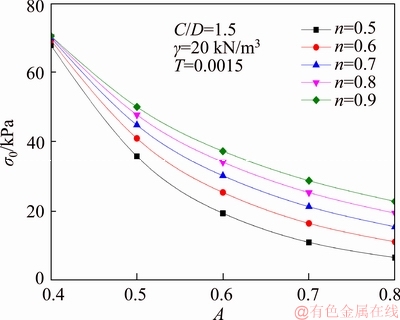
Figure 4 Influence of A and n on face pressures σ0
Figure 5 Influence of A and n on face pressures σ0 (T=0)
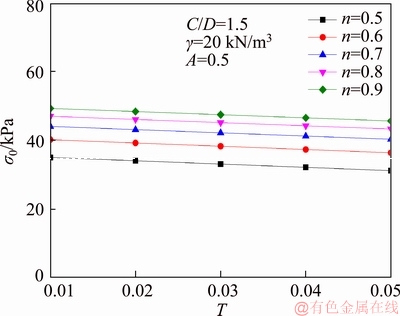
Figure 6 Influence of T and n on the face pressures σ0
Figure 6 presents the influence of T and n on necessary face pressure σ0 when the dimensionless parameter A=0.5, T changes from 0.01 to 0.05 and N is equal to 0.5, 0.6, 0.7, 0.8, 0.9, respectively. It can be seen from the figure that under the same condition of n, the necessary face pressure σ0 decreases with the increase of T, and increases with the increase of n.
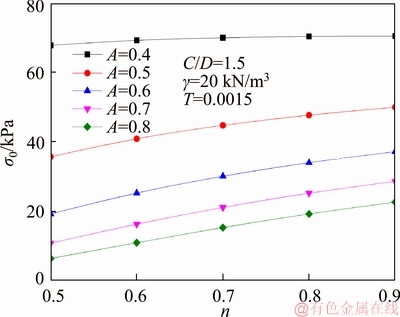
Figure 7 Influence of n and A on face pressures σ0
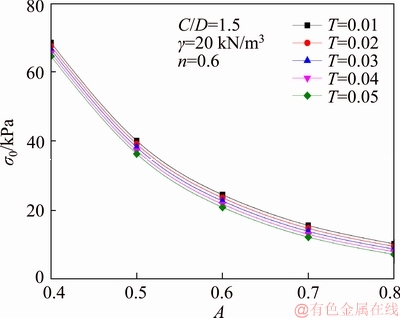
Figure 8 Influence of A and T on face pressures σ0
Figure 7 studies the influence of A and n on necessary face pressure σ0 when the dimensionless parameter T=0.0015, n changes from 0.5 to 0.9 and A is 0.4, 0.5, 0.6, 0.7, 0.8, respectively. It can see from the diagram that for a fixed T, the face pressure σ0 increases with the increase of A and n.
Figure 8 presents the influence of A and T on face pressure σ0 when the dimensionless parameter n=0.5, A changes from 0.4 to 0.8 and T is 0.01, 0.02, 0.03, 0.04, 0.05, respectively. It can be seen from the graph that the face pressure σ0 decreases with the increase of A, and decreases with the increase of T for the same value of A.
The influence of depth ratio on the shape of the failure mechanism is shown in Figure 9(a). It can be seen from the figure that the change in the depth ratio does not affect the shape of the failure mechanism, but it is related to whether the failure shape reaches the ground surface. If the depth ratio is small (e.g. 1.0), the failure mode reaches the ground surface, and it does not when the ratio is more than 1.5.
The effects of the dimensionless parameters A, T, and n on the failure mode are shown in Figures 9(b)-(d). It can be seen from the diagram that when A is reduced, the region of the failure mechanism is increased forward gradually. T has no effect on the shape of the failure mechanism. When n increases, the size of the failure mechanism decreases.
8 Project case
This section takes the Taxia Tunnel as an engineering example, which is located in the Lishui county, Zhejiang Province, China. The total length of the Taxia Tunnel is 172 m, the maximum depth is 415 m, and the average depth is 200 m. The radius of the tunnel is 4 m. According to site survey, the mechanical parameters of rock mass are obtained as γ=20 kN/m3, c=0.2 MPa, φ=27°. According to the method in this paper, the theoretical surrounding rock pressure is calculated as σ0=368 kPa. In order to monitor the surrounding rock pressure of the tunnel roof, the pressure box is installed between the top lining and the surrounding rock, and two pressure boxes are installed every 40 m, and finally a larger value is obtained. Through 50 d observation, the change of surrounding rock pressure of the Taxia Tunnel is shown in Figure 10.
Figure 10 shows that the tunnel surrounding rock pressure calculated by the paper is close to the actual monitoring surrounding rock pressure. The upper and lower errors vary within 50 kPa. It can meet the engineering design accuracy.
9 Conclusions
1) To n=1, the nonlinear Baker failure criterion is degenerated to a linear Mohr-Coulomb strength criterion. Two failure criteria are applied to calculating the necessary face pressures respectively. The calculated results based on 5 sets of parameters are almost the same, and the proposed method is verified.
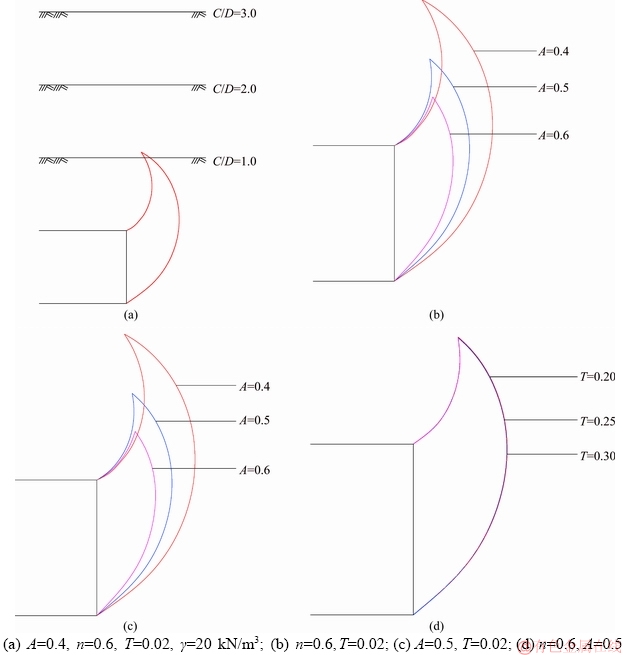
Figure 9 Influence of various parameters on failure mechanism:
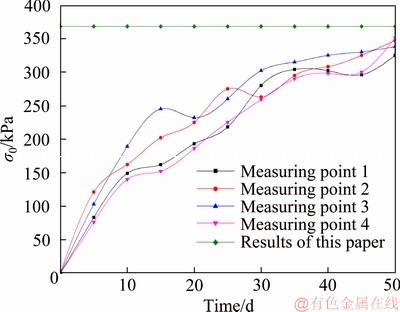
Figure 10 Comparison between this paper and engineering examples
2) The influence of the parameter A which characterizes the material shear strength on the critical face pressures is very significant. The necessary face pressure nonlinearity decreases with the increase of A. The influence of n on the face pressures is also important; the critical face pressure nonlinearity increases with the increase of n. The influence of T on the face pressures is small, and it shows a linear decreasing trend.
3) With the decrease of A, the range of the failure mechanism is expanding. When n is reduced, the range is also increasing, but the effect is not significant. The impact of T on the range of failure mechanism is almost negligible.
References
[1] CHEN W F. Limit analysis and soil plasticity [M]. Amsterdam: Elsevier Scientific Pub. Co, 1975.
[2] ZHU J Q, YANG X L. Probabilistic stability analysis of rock slopes with cracks [J]. Geomechanics and Engineering, 2018, 16(6): 655-667.
[3] ZHANG Biao, WANG Xuan, ZHANG Jia-hua, CHENG Hao. Safe range analysis of clear distance of twin shallow tunnels based on limit analysis and reliability theory [J]. Journal of Central South University, 2018, 25(1): 196-207.
[4] WANG Hui, ZHEN Peng-qiang, ZHAO Wen-juan, TIAN Hong-ming. Application of a combined supporting technology with U-shaped steel support and anchor-grouting to surrounding soft rock reinforcement in roadway [J]. Journal of Central South University, 2018, 25(5): 1240-1250.
[5] VAGHEFI M, AHMADI A, FARAJI B. Variation of hydraulic parameters with different wing of a T-shape spur dike in bend channels [J]. Journal of Central South University, 2018, 25(3): 671-680.
[6] ABID A, LYAMIN A V, HUANG J S, SLOAN S W, CASSIDY M J. Undrained stability of a single circular tunnel in spatially variable soil subjected to surcharge loading [J]. Computers and Geotechnics, 2017, 84: 16-27.
[7] DANIEL W W, ANDREW J A, SCOTT W S, ANDREI V L. Undrained stability of a square tunnel where the shear strength increases linearly with depth [J]. Computers and Geotechnics, 2013, 49: 314-325.
[8] KENTARO Y, ANDREI V L, DANIEL W W, SCOTT W S, ANDREW J A. Stability of dual circular tunnels in cohesive-frictional soil subjected to surcharge loading [J]. Computers and Geotechnics, 2013, 50: 41-54.
[9] XU Jing-shu, YANG Xiao-li. Seismic stability of 3D soil slope reinforced by geosynthetic with nonlinear failure criterion [J]. Soil Dynamics and Earthquake Engineering, 2019, 118: 86-97.
[10] SALVADOR S, RAFAEL J. A tunnel face failure mechanism for layered ground, considering the possibility of partial collapse [J]. Tunnelling and Underground Space Technology, 2015, 47: 182-192.
[11] NIMA K, HISHAM M, MOHSEN H, BEHZAD F. The stability of shallow circular tunnels in soil considering variations in cohesion with depth [J]. Tunnelling and Underground Space Technology, 2015, 49: 230-240.
[12] GUAN Z, ZHU W C, NIU L L, WANG Q Y. Three- dimensional upper bound limit analysis of supported cavity roof with arbitrary profile in Hoek-Brown rock mass [J]. Tunnelling and Underground Space Technology, 2017, 69: 147-154.
[13] LI Zheng-wei, YANG Xiao-li. Active eearth thrust considering tension crack, pore-water pressure and soil nonlinearity [J]. KSCE Journal of Civil Engineering, 2019, 23(1): 56-62.
[14] LI Yong-xin, YANG Xiao-li. Three-dimensional seismic displacement analysis of rock slopes based on Hoek-Brown failure criterion [J]. KSCE Journal of Civil Engineering, 2018, 22(11): 4334-4344.
[15] XU Jing-shu, LI Yong-xin, YANG Xiao-li. Seismic and static 3D stability of two-stage slope considering joined influences of nonlinearity and dilatancy [J]. KSCE Journal of Civil Engineering, 2018, 22(10): 3827-3836.
[16] PAN Qiu-jing, DIAS D. Upper-bound analysis on the face stability of a non-circular tunnel [J]. Tunnelling and Underground Space Technology, 2017, 62: 96-102.
[17] PAN Qiu-jing, DIAS D. Three dimensional face stability of a rock tunnel subjected to seepage forces [J]. Tunnelling and Underground Space Technology, 2018, 71: 555-566.
[18] MEHDI P, HAMID K, MOHAMMAD A, HAMID A, JAFAR A M. Stability analysis of shallow tunnels subjected to eccentric loads by a boundary element method [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2016, 4(8): 480-488.
[19] LI T Z, YANG X L. Probabilistic stability analysis of subway tunnels combining multiple failure mechanisms and response surface method [J]. International Journal of Geomechanics, 2018, 18(12): 04018167.
[20] JAGDISH P S, JYANT K. Stability of a circular tunnel in presence of pseudostatic seismic body forces [J]. Tunnelling and Underground Space Technology, 2014, 42: 264-276.
[21] SEUNG H K, FULVIO T. Face stability and required support pressure for TBM driven tunnels with ideal face membrane - Drained case [J]. Tunnelling and Underground Space Technology, 2010, 5(25): 526-542.
[22] ZHANG Cheng-ping, HAN Kai-hang, ZHANG Ding-li. Face stability analysis of shallow circular tunnels in cohesive–frictional soils [J]. Tunnelling and Underground Space Technology, 2015, 50: 345-357.
[23] YANG X L, ZHOU T, LI W T. Reliability analysis of tunnel roof in layered Hoek-Brown rock masses [J]. Computers and Geotechnics, 2018, 104: 302-309.
[24] DONALD I B, CHEN Zu-yu. Slope stability analysis by the upper bound approach: Fundamentals and methods [J]. Canadian Geotechnical Journal, 1997, 34(11): 853-862.
[25] BAKER R. Non-linear strength envelopes based on triaxial data [J]. ASCE Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(5): 498-506.
[26] JIANG J C, BAKER R, YAMAGAMI T. The effect of strength envelope nonlinearity on slope stability calculations [J]. Canadian Geotechnical Journal, 2003, 40(2): 308-325.
[27] BAKER R, FRYDMAN S. Upper bound limit analysis of soil with non-linear failure criterion [J]. Soils and Foundations, 1983, 23(4): 34-42.
[28] ZHAO Yan-lin, WANG Yi-xian, WANG Wei-jun, WAN Wen, TANG Jin-zhou. Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 93: 66-75.
[29] ZHANG Dao-bing, LIU Zhi-zhen, ZHANG Jia-hua. A new failure mechanism for deep cavity and upper bound solution of supporting pressure [J]. Journal of Central South University, 2017, 24(9): 2082-2091.
[30] LI Zheng-wei, YANG Xiao-li. Active earth pressure for soils with tension cracks under steady unsaturated flow conditions [J]. Canadian Geotechnical Journal, 2018, 55(12), 1850- 1859.
[31] LI Yong-xin, YANG Xiao-li. Soil-slope stability considering effect of soil-strength nonlinearity [J]. International Journal of Geomechanics, 2019, 19(3): 04018201.
[32] LUO W J, YANG X L. 3D stability of shallow cavity roof with arbitrary profile under influence of pore water pressure [J]. Geomechanics and Engineering, 2018, 16(6): 569-575.
[33] MOLLON G, PHOON K K, DIAS D, SOUBRA A H. Validation of a new 2d failure mechanism for the stability analysis of a pressurized tunnel face in a spatially varying sand [J]. Journal of Engineering Mechanics, 2010, 137: 8-21.
[34] ZHANG J H, WANG W J, ZHANG D B, ZHANG B, MENG F. Safe range of retaining pressure for three- dimensional face of pressurized tunnels based on limit analysis and reliability method [J]. KSCE Journal of Civil Engineering, 2018, 22(11): 4645-4656.
(Edited by HE Yun-bin)
中文导读
基于Baker准则浅埋巷道掌子面稳定性的上限分析
摘要:将非线性Baker破坏准则引入到极限分析上限定理中,分析浅埋巷道掌子面的稳定性问题。从能量角度分析极限状态下掌子面的受力状态,计算破坏过程中所产生的外功率和内能损耗率,推导围岩压力的解析解,采用Matlab软件序列二次规划算法得到围岩压力的最优上限解。研究结果表明,非线性Baker破坏准则中的三个无量纲参数A,T,n对掌子面围岩压力以及破坏范围的影响均各不相同。A的影响最大,n次之,T最小;并且当A减小时掌子面的围岩压力和破坏范围均非线性增大。结合浙江省丽水市隧下隧道的实际监测资料,对计算结果进行了验证。建议针对软岩巷道应及时加强掌子面的支护措施,防止发生坍塌事故。
关键词:非线性Baker破坏准则;掌子面;稳定性;极限分析法;围岩压力
Foundation item: Projects(51674115, 51804113) supported by the National Natural Science Foundation of China; Project(17B095) supported by the Excellent Youth Subsidy Project of Hunan Provincial Department of Education, China
Received date: 2018-11-26; Accepted date: 2019-05-15
Corresponding author: ZHANG Dao-bing, PhD, Associate Professor; Tel: +86-13975264336; E-mail: dbzhang@hnust.edu.cn; ORCID: 0000-0001-9901-5592
Abstract: The nonlinear Baker failure criterion is introduced into the upper-bound limit analysis to examine the face stability of a shallow tunnel. The tunnel face under the ultimate limit state is analyzed from the perspective of energy balance. The work rates of external forces and internal energy dissipation are calculated. An analytical solution of necessary face pressures is derived. The optimal upper-bound solution of the face pressures is obtained by optimization. The results show that the three dimensionless parameters A, T, n of nonlinear Baker failure criterion have different effects on the necessary face pressures and the pattern failure mechanisms ahead of tunnel face. A is the most important one; n takes the second place, and T is the least one. The computed necessary face pressures are nonlinearly increasing when A is reduced. Combined with the actual monitoring data of Taxia tunnel, the calculation results in this paper is verified. It is suggested that the tunnel face supports should be strengthened timely in soft rocks to prevent the occurrence of face collapse.


