
J. Cent. South Univ. (2020) 27: 500-516
DOI: https://doi.org/10.1007/s11771-020-4312-3

A hybrid approach for evaluating CPT-based seismic soil liquefaction potential using Bayesian belief networks
MAHMOOD Ahmad1, 2, TANG Xiao-wei(唐小微)1, QIU Jiang-nan(裘江南)3,GU Wen-jing(谷文静)3, FEEZAN Ahmad4
1. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology,Dalian 116024, China;
2. Department of Civil Engineering, University of Engineering and Technology Peshawar (Bannu Campus),Bannu 28100, Pakistan;
3. Faculty of Management and Economics, Dalian University of Technology, Dalian 116024, China;
4. Department of Civil Engineering, Abasyn University, Peshawar 25000, Pakistan
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract:
Discernment of seismic soil liquefaction is a complex and non-linear procedure that is affected by diversified factors of uncertainties and complexity. The Bayesian belief network (BBN) is an effective tool to present a suitable framework to handle insights into such uncertainties and cause–effect relationships. The intention of this study is to use a hybrid approach methodology for the development of BBN model based on cone penetration test (CPT) case history records to evaluate seismic soil liquefaction potential. In this hybrid approach, naive model is developed initially only by an interpretive structural modeling (ISM) technique using domain knowledge (DK). Subsequently, some useful information about the naive model are embedded as DK in the K2 algorithm to develop a BBN-K2 and DK model. The results of the BBN models are compared and validated with the available artificial neural network (ANN) and C4.5 decision tree (DT) models and found that the BBN model developed by hybrid approach showed compatible and promising results for liquefaction potential assessment. The BBN model developed by hybrid approach provides a viable tool for geotechnical engineers to assess sites conditions susceptible to seismic soil liquefaction. This study also presents sensitivity analysis of the BBN model based on hybrid approach and the most probable explanation of liquefied sites, owing to know the most likely scenario of the liquefaction phenomenon.
Key words:
Cite this article as:
MAHMOOD Ahmad, TANG Xiao-wei, QIU Jiang-nan, GU Wen-jing, FEEZAN Ahmad. A hybrid approach for evaluating CPT-based seismic soil liquefaction potential using Bayesian belief networks [J]. Journal of Central South University, 2020, 27(2): 500-516.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-020-4312-31 Introduction
Assessment of seismic soil liquefaction potential is a probabilistic issue rather than deterministic owing to the complexity and uncertainty involved in earthquake and soil parameters and site conditions.
Previous deterministic methods of seismic soil liquefaction potential present no insight to the liquefaction probability and offer only whether seismic soil liquefaction occurs or not. Therefore,presently probabilistic methods can better cater engineering requirements of seismic risk analysis. In recent few decades, with the increasing accumulation of in-situ data, soft computing methods, such as artificial neural network (ANN) [1-3], support vector machine (SVM) [4-6], relevance vector machine (RVM) [7], stochastic gradient boosting (SGB) [8] and genetic programming (GP) [9, 10], have been used to evaluate the potential of seismic soil liquefaction. Nevertheless, most of the existing soft computing methods have the following limitations [11]: 1) due to limited use of prior knowledge, they can not easily conclude the assessment results; 2) they remain difficult to integrate various information sources into one unified system; 3) they are not proficient in assessing uncertainty.
Bayesian belief network (BBN) is a proficient tool for knowledge presentation and reasoning under the influence of uncertainties [12]. It can integrate domain knowledge (DK) and various source data into a coherent system, primarily, it allows not only sequential inference (from causes to results) but also reverse inference (from results to causes). Recently, BBN has been used widely in diversified fields such as regional risk assessment [13], seismic hazard assessment [14, 15], risk assessment for buildings [16-18], loss assessment [19, 20], optimization and reliability [21-23]. WEBER et al [24] conducted a comprehensive review of the application of BBN in risk analysis in 2010. However, limited research work is reported in the literature regarding assessment of seismic soil liquefaction potential using BBN. JUANG et al [25] developed a probability-based liquefaction potential assessment method using logistic regression and Bayesian mapping. BAYRAKTARLI [26] explained the application of BBN in assessing seismic soil liquefaction. HUANG et al [27] considered parameters uncertainty to determine the model uncertainty of seismic soil liquefaction evaluation model. HU et al [28] proposed a BBN model based on standard penetration test (SPT) case histories in sandy soils. In this study, the intention is to use a hybrid approach methodology using K2 algorithm and DK for the development of probabilistic graphical model based on cone penetration test (CPT) case history records data to assess seismic soil liquefaction potential. The study examines the capability of CPT-based BBN model developed by hybrid approach with the C4.5 decision tree (DT) and available artificial neural network models in literature. This study also presents sensitivity analysis of the BBN model based on hybrid approach and the most probable explanation of liquefied sites.
This paper is structured into seven sections. In Section 2, the basics of BBN are summarized. Section 3 describes the details of hybrid approach for the development of a BBN model. The development of probabilistic BBN models is presented in Section 4, which is the main objective of this work. Section 5 presents the evaluation measures which include metrics of overall accuracy, Matthews correlation coefficient (MCC), recall, precision and F-measure. Results of training (74 cases) and testing (35 cases) phases of BBN models are compared and validated with the available models in literature in Section 6, and Section 7 sets out the most relevant conclusions and future work of the study.
2 Basics of Bayesian belief network
Bayesian belief network is a graphical model that allows a probabilistic relationship between a set of variables [12]. BBN is a directed acyclic graph (DAG), which consists of nodes and arcs. Nodes denote variables of interest, and the arcs among them represent causal relationships or dependencies between variables [12, 22, 23]. The absence of an arc among two variables is a sign of conditional independence between the respective variables. The BBN is composed of the following components as depicted in Figure 1:
1) Variables set (e.g. B1, B2 and B3) and directed arcs linking the variables;
2) Mutually exclusive states for each variable (e.g. for B1 and B2 the states are High, Medium and Low);
3) Specified conditional probability for each variable by parents (e.g. for B3).
In the BBN, relationships among the variables are represented in the form of family relationship, where a variable B1 is called to be the parent of B3 and B3 is the child of B1. The dependencies are measured by the conditional probability table of each node in a given network; for variables without parents, the probabilities are reduced to an unconditional probability (UP) (e.g. B1 and B2 in at Table 1). The effectiveness of BBN lies in its flexibility to acquire top-down inference,considering the cause (or parent) and inferring the possible effect (or child), and bottom-up inference, considering the effect (child) and inferring the possible cause (parent). The posterior probability can be found by using Bayesian formulas and conditional independence rule as follows:
 (1)
(1)
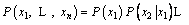
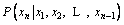 (2)
(2)
 (3)
(3)
where P(X|Y) is one’s belief for hypothesis X upon observing evidence Y which is termed as posterior probability; P(Y|X) is the likelihood that Y is observed if X is true; P(Y) is called prior probability that the hypothesis holds true; P(X) is the probability that the evidence takes place, and π(xi) is a set of values for the parent of xi. In seismic soil liquefaction, a lot of historic information about liquefaction are accumulated, for instance liquefaction surface manifestation, relationship between significant factors of soil liquefaction, and standard specification, which can be served as an effective prior knowledge for fixing the BBN structure. Therefore, the prior knowledge is utilized to develop the structure of BBN models to prevent unreasonable relationships caused by overfitting, and data learning is utilized to acquire the conditional probability tables of nodes in the network structure.

Figure 1 Schematic of Bayesian belief network
Table 1 Conditional probability table

3 Hybrid approach
In this section hybrid approach for the development of a BBN model is highlighted. The naive model is developed initially by using interpretive structural modeling (ISM) approach which is based on DK. DK is a specific, specialized and valid field knowledge that can provide certain information, such as the relationship between variables, from the literature review or from field experts. The naive model built by ISM approach can thereafter provide several significant information in the K2 algorithm to perform structure-based learning from the CPT case history records data to develop a BBN model.
3.1 Naive model based on ISM
The ISM methodology was presented by WARFIELD [29] to study complex socioeconomic systems. ISM can be used as a systematic means to recognize the contextual relationships between the measured elements linked with an issue to be examined. The ISM approach has been effectively utilized in diversified set of problems, for instance identification and benchmark of seismic soil liquefaction significant factors [30], risk management in supply chains [31], and energy conversation [32]. ISM can be illustrated in the subsequent steps, for the present study, as suggested by SUSHIL [33]:
Step 1: Identification of factors related to the problem or issue through literature review, etc.
Step 2: Fixing the contextual relationships between such factors, i.e., V (row factor influences the column factor), A (column factor influences the row factor), O (no relationship between the row and column factors), or X (bidirectional relations from row to column and column to row factors) according to domain knowledge whether or not one factor leads to another.
Step 3: Construct a structural self-interaction matrix (SSIM) based on comparison.
Step 4: SSIM is converted to initial reachability matrix, by replacing 1 or 0 for the original symbols, V, A, X and O as per the rules for transformation.
Step 5: Transitivity of the initial reachability matrix is checked in order to develop the final reachability matrix. The transitive relationships mean that if variable d is associated with variable e and variable e is associated with variable f, then variable d is certainly associated to variable f.
Step 6: The reachability and antecedent sets of factors are developed from the final reachability matrix. The reachability set for a particular factor includes the factor itself and other factors which it may achieve, and antecedent set includes factor itself and other factors that can help achieve it. Subsequently, the intersection of these sets is found for the entire factors. The factor for reachability and intersection sets are identical listed in the first level. This factor is then separated from other factors for the next iteration process. Repeat the same level of iteration process until all levels of each factor are established.
Step 7: Removing the transitivity links and drawing a directed graph (digraph) from the final reachability matrix.
Step 8: Converting the digraph into an ISM-based hierarchical model by replacing the nodes with statements.
Step 9: The conceptual discrepancy of model is verified and improved for necessary modifications and corrections.
The hierarchical structure can be easily constructed according to the steps mentioned above and more details can be found in Section 4.3.
3.2 BBN model based on hybrid approach
BBN is a probabilistic graphical network based upon Bayes’ theorem, which constitutes a dynamic theoretical model in the field of uncertain knowledge representation and reasoning. The development of BBN model is complicated and could be constructed in any one of three ways: 1) based on DK; 2) using algorithms to directly learn from the data; 3) combining DK and machine learning algorithm. The third method is typically utilized in practical applications with large number of variables and immense datasets, as it not only decreases the search space by integrating prior DK, but also affirms the effectiveness of the model.
AHMAD et al [34] investigated the performance of K2 machine learning (ML) algorithm to evaluate earthquake-induced liquefaction potential of soil using Bayesian belief network learning software, Netica, and found that BBN-K2 model outperform the Tabu search and Hill climbing BBN models in terms of predictive performance measures. The algorithm has low data dependence in structure learning process and is a score-based method that may be used to perform actual data analysis and fitting, as proposed by COOPER et al [35]. Therefore, K2 algorithm is used in this work. The algorithm has several requirements: 1) variables in the dataset are discrete; 2) events are independent; 3) acquired data are integrated; 4) order of the entire nodes is defined; 5) the maximum parent nodes are identified.
4 Development of probabilistic BBN models
4.1 CPT case history records data for seismic soil liquefaction
The CPT case history records data collected by GOH ANTHONY [2] is used in this study. It includes 109 case records mainly from sites having level ground conditions with sand or silty sand deposits. The data consisted of 79 case records from China, 16 from Japan, 9 from Unites States, and 5 from Romania, and they are all taken from 5 earthquakes that occurred in the period of 1964-1983. In all 109 case records, 74 sites contained surface evidence of liquefaction, 35 sites did not contain. The ratio of liquefaction to non-liquefaction cases is 2.11:1, which indicates that there is class imbalance in the case records. The descriptive statistics of the CPT case history records data is shown in Table 2.
The output consisted of a single node representing the liquefaction potential. The node was given a binary class of yes for liquefied sites and a class of no for non-liquefied sites. In the present study, a total of 74 case records are considered for the training phase, and other remaining 35 case records are considered for the testing phase. The training and testing case records are the same as the ones used by GOH ANTHON [2] and ARDAKANI et al [36]. The records of the training and testing phases are summarized in Tables 3 and 4, respectively. τ/σ'v denotes the cyclic stress ratio.
4.2 Parameters selection
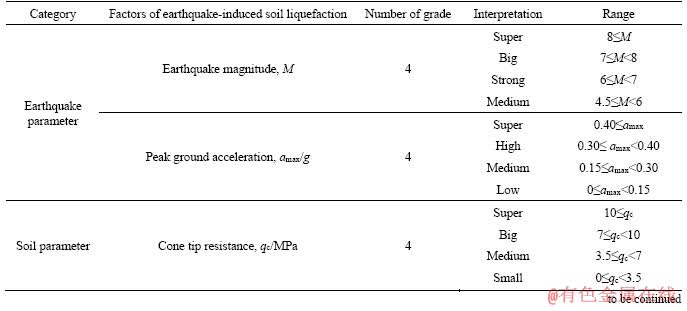
There are numerous factors affecting the soil liquefaction caused by earthquakes, such as earthquake magnitude, peak ground acceleration, closest distance to rupture surface, depth of soil deposit, groundwater level, cone tip resistance etc. The general principle of selecting parameters of seismic soil liquefaction [37] are: 1) main contributing factors; 2) factors presented in mostly field case records data; 3) factors that are simply to ascertain and assess. Bearing in mind the cited points and the limitation of the significant factors in the case history records, we considered five significant factors in this paper, namely earthquake magnitude, peak ground acceleration, cone tip resistance, mean grain size, and effective vertical stress same as the factors used by GOH ANTHONY [2]. In order to fulfill the first demand of the K2 algorithm, earthquake magnitude, peak ground acceleration, mean grain size and vertical effective stress factors of seismic soil liquefaction are graded according to HU et al [38] grading standard criteria as shown in Table 5. While the cone tip resistance is divided into four grades that are super (10 MPa≤qc), big (7 MPa≤qc<10 MPa), medium (3.5 MPa≤qc<7 MPa), and small (0≤qc<3.5 MPa) as per the statistical aspect-mean and domain knowledge. Optimal multi-splitting discretization algorithm [39] can be used to automatically determine the optimal subdivisions and to discretize factors for BBN. The liquefaction potential given 0 (non-liquefied sites) and 1 (liquefied sites) values as the output was.
4.3 BBN models based on ISM and K2-DK
In order to develop naive model based on ISM technique, in step 1, we identified the factors that are most related to the seismic soil liquefaction. Five significant factors of seismic soil liquefaction are considered as described in Section 4.2. These factors are earthquake magnitude (F1), peak ground acceleration (F2), cone tip resistance (F3), mean grain size (F4), vertical effective stress (F5), and liquefaction potential (F6).
In step 2, the interrelationship between these factors is obtained. Since ISM methodology proposes the use of DK in developing the contextual relationship between factors, so relationships are ultimately examined by the field experts who approved the contextual relationship between seismic soil liquefaction factors (Table 6).
In step 3, structural self-interaction matrix for seismic soil liquefaction potential factors is converted to a binary matrix, called the initial reachability matrix, by replacing with 1 or 0 for the original symbols as shown in Table 7.
Table 2 Statistical aspects of seismic soil liquefaction data
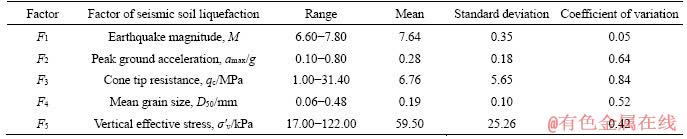
Table 3 Summary of training data

Continued
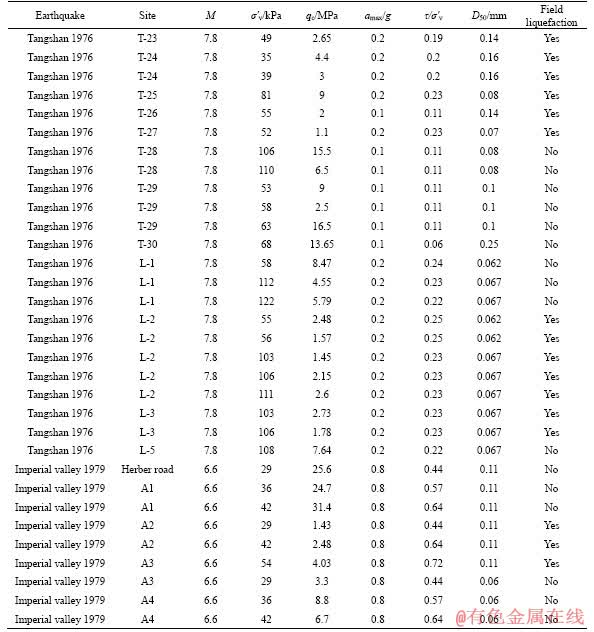
Table 4 Summary of testing data

Continued

Table 5 Grading standards for seismic soil liquefaction factors
Continued

Table 6 Structural self-interaction matrix for seismic soil liquefaction factors

After obtaining initial reachability matrix, the transitivity property is checked to obtain the final reachability matrix as discussed in Section 3.1. The final reachability matrix with the driving and dependence power is shown in Table 8.
Table 7 Initial reachability matrix

In step 5, the factors together with their reachability set, antecedent set and intersection set are used for deriving multilevel hierarchy structure levels are shown in Table 9. Results revealed that there are three levels partition as follows:L1={F6}; L2={F2, F3}; L3={F1, F4, F5}.
For next steps, multilevel hierarchy structure of seismic soil liquefaction potential is developed from the final reachability matrix. The transitivity links among two factors such as the direct link between mean grain size and liquefaction potential is removed owing that the mean grain size can affect the soil liquefaction via cone tip resistance.
Table 8 Final reachability matrix

In the last step, there is no conceptual discrepancy in the structural model, so the interpretive structural model for seismic liquefaction is shown in Figure 2. In the interpretive structural model, there is a restriction of no direct relation among skipping-level’s nodes, for example, earthquake magnitude and liquefaction potential.
The following interpretation are concluded from the cited above naive model based on ISM (Figure 2): 1) the order of the nodes is earthquake magnitude (M), mean grain size (D50), vertical effective stress (σ'v), peak ground acceleration (amax), cone tip resistance (qc), and liquefaction potential; 2) restriction number of the parent nodes is 5; and 3) some nodes are not related to other nodes in the same level or next level. For instance, peak ground acceleration is not related to the cone tip resistance at the same level, and vertical effective stress is not related to peak ground acceleration in the next level. Once the useful information is integrated into K2 algorithm and structure learning is carried through learning 74 case history records data as shown in Table 3, FullBNT-1.0.7 is utilized to conduct structure learning via MATLAB. The Bayesian belief network structure is finally developed, as shown in Figure 3. The network is composed by 6 nodes and several lines. The 6 nodes refer to 6 variables, and the lines between nodes indicate the relationships among the variables.
Table 9 Level partition-iteration

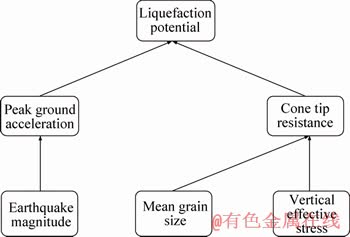
Figure 2 ISM of seismic soil liquefaction potential
The ISM, K2 and DK network structures of seismic soil liquefaction are directly constructed in Netica free version software to perform parameter learning, because acquiring conditional probability distribution of the nodes and Bayesian belief network models are determined to assess the liquefaction potential of seismic soil. Comparing these two models, the BBN-K2 and DK model developed by the hybrid method compensates the limitations of other models: 1) skipping-level’s factors are connected (e.g. the earthquake magnitude and liquefaction potential); and 2) some factors connections are avoided by integrating DK (e.g. earthquake magnitude is linked to cone tip resistance). The graphical results of seismic soil liquefaction of both BBN models are presented in Figure 4.

Figure 3 BBN structure for earthquake-induced soil liquefaction based on K2 algorithm and DK
5 Evaluation measures
BBN models are compared with the C4.5 decision tree and ANN models available in literature to examine their capability. To measure the performance of the BBN models, several metrics are used, namely, overall accuracy (OA, a), Matthews correlation coefficient (MCC, cm), precision (p), recall (r), and F-measure (mF). These metrics can be computed from confusion matrix in Table 10.
In binary class case, i.e., liquefaction and non-liquefaction, there are four possible outputs for a single prediction. The true negative (TN) and true positive (TP) are correct classification [40]. The false positive (FP) represents that the outcome is wrongly predicted as positive while a false negative (FN) occurs when the output is wrongly classified as negative. Overall accuracy is a measure of the total number of predictions that were correct. a is computed as follows:
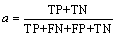 (4)
(4)
In seismic soil liquefaction problem, liquefaction cases are usually more than non- liquefaction cases so it may be deceptive when evaluating the predictive ability based on the OA alone owing to the class imbalance in the data set. The best choice is F-measure, which combined precision and recall into a single evaluation index to predict the performances of binary classification model. Precision measures the accuracy of the predictions for a single class (liquefaction instances or non- liquefaction instances), whereas the recall measures accuracy of predictions only considering predicted values. They can be found from the confusion matrix as:
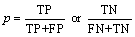 (5)
(5)
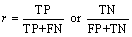 (6)
(6)
 (7)
(7)
mF has ranged from 0 (worst value) to 1 (best value).

Figure 4 Graphical results of seismic soil liquefaction potential models:
Table 10 Confusion matrix

In this study, Matthews correlation coefficient is used to present the degree of correlation between observed and predicted classes and is expressed as:
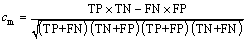 (8)
(8)
The value range of cm is [-1, 1], where 1 means complete agreement; -1 means complete inconsistency; and 0 means that the prediction is independent of the observed results.
6 Results and discussion
6.1 Performance comparison of training data
Performance of the BBN models was compared with C4.5 decision tree model in present study and with ANN model in Ref. [2] on 74 CPTs (48 liquefaction cases and 26 non-liquefaction cases) training phase data. The results of the training data set that included various metrics such as overall accuracy, MCC are presented in Table 11. Comparing OA, the BBN-K2 and DK model in present study showed at par performance with ANN model developed by GOH ANTHONY [2] for the same input factors and training phase data. As OA cannot be used alone, model performance may be deceptive owing to the class imbalance in the data set and this performance is higher when liquefied samples in the majority class are favorably predicted. Therefore, F-measure was used. In case of yes class (liquefaction) all the models showed at par recall value (i.e., 0.979) whereas in case of precision, the BBN-K2 and DK and ANN [2] models showed highest value (i.e., 1.000); when F-measure is calculated the BBN-K2 and DK and ANN [2] models have the highest value (i.e., 0.989) for yes class. For no class, the BBN-K2 and DK and ANN model [2] have the same highest recall, precision, and F-measure whereas BBN-ISM has the worst performance. Moreover, BBN-K2 and DK and ANN [2] models have the highest value of MCC relative to the BBN-ISM and C4.5 DT models. Generally, BBN-K2 and DK showed compatible and at par performance results with ANN [2] model and relatively better performed than the C4.5 DT and BBN-ISM models for liquefaction and non-liquefaction cases in training phase data.
6.2 Predictive performance comparison of testing data
The predictive performance results of the BBN, C4.5 DT and ANN [2] models on the remaining 35 cases (26 liquefaction cases and 9 non-liquefaction cases) are shown in Table 12. It can be noted clearly that the ANN [2] model has the slightly better than the BBN-K2 and DK, ISM and C4.5 DT models in terms of MCC and F-measure for non-liquefaction instances. It is worthwhile to mention that the accuracy of the ANN [2] model for no class (non-liquefied) instances is better than the yes class (liquefied) instances which does not match the requirement of the engineering practice, whereas both BBN and C4.5 DT models showed opposite pattern. The BBN model provides an appropriate understandable semantic interpretation framework to predict seismic soil liquefaction and handle insights into cause–effect relationships and uncertainties. Whereas, the knowledge acquired by the ANN model in the training stage is stored implicitly, and it is very difficult to reasonably explain the overall structure of the network. Therefore, the ANN model has little insight into the basic mechanism of the problem. In general, all the models performed well in the testing data phase and it revealed that the predictive performance should be further investigated for larger dataset with almost no class imbalance in the database and sampling bias in training and testing phases.
Table 11 Performance evaluation of training phase case history records

Table 12 Predictive performance evaluation of testing phase case history records

6.3 Analysis of BBN-K2 and DK model
6.3.1 Comparison with available C4.5 DT model in literature
To compare and validate the proposed BBN-K2 and DK model which was developed by hybrid approach it is compared with C4.5 DT model [36] in Table 13. As shown, the BBN-K2 and DK model developed by hybrid approach performs most similar with the C4.5 DT model although with only difference of one additional parameter i.e., cyclic stress ratio was used by ARDAKANI et al [36] for same training and testing data sets. It should be noted that the BBN-K2 and DK model is developed based on 5 direct significant factors while the C4.5 DT used cyclic stress ratio which is an indirect parameter and required determination. It is also noted that increasing the number of input factors or variables using C4.5 DT algorithm the predictive accuracy increased by 2.857% in testing data.
In this study, we focus to construct a BBN model based on effective hybrid approach to evaluate accurately seismic soil liquefaction potential. Comparatively in terms of training and testing data performance, the BBN-K2 and DK model is relatively better than BBN-ISM model. Considering the BBN-K2 and DK model compatibility with ANN model [2] in its OA, MCC, recall, precision, F-measure, simplicity to perform in practice and adaptive nature, the use of BBN-K2 and DK model in evaluating earthquake-induced soil potential is quite promising. The proposed BBN-K2 and DK model can continuously upgrade its conditional probability table of each node to enhance its predictive strength while new data is integrated. The BBN-K2 and DK model also has some limitations, such as heavily relying on large amounts of data and the learning requirements of K2 algorithm. It is not suitable for incomplete data.
Since the present study is a data-driven approach without resorting to the fundamental physics of liquefaction. Advanced numerical modeling such as micromechanical [41, 42], modified bounding surface hypoplasticity [43] and coupled numerical model (fluid-structure-seabed interaction CAS 2D) [44], can be used to study fundamental mechanism of liquefaction phenomenon and related hazards once well calibrated.
6.3.2 Sensitivity analysis
The sensitivity analysis function of Netica software is utilized to find which factors have more influence in seismic soil liquefaction potential. The liquefaction potential node is selected to make sensitivity analysis in Netica and the result is listed in Table 14. Table 14 presents that the mutual info of 0.03882 of cone tip resistance (qc) is the largest, which interprets that it has the strongest influence on soil liquefaction, followed by peak ground acceleration and vertical effective stress, which have mutual info of 0.00529 and 0.00329, respectively. These results are highly consistent with Ref. [45], whereas the earthquake magnitude is least sensitive factor which has mutual info of 0.00180.
Table 13 Comparison of BBN-K2 and DK model and C4.5 DT model

Table 14 Sensitivity analysis result of liquefaction potential

6.3.3 Most probable explanation
Netica function is utilized to draw the most probable explanation (MPE) to perceive which scenario is most likely the cause set of earthquake- induced liquefaction potential. The developed BBN-K2 and DK model is used to make the MPE and the result is shown in Figure 5.
The combination of MPE cause set is that the cone tip resistance, qc and vertical effective stress, σ'v are in small grade (0≤qc<3.5 MPa and 0≤σ'v<50 kPa), peak ground acceleration, amax and mean grain size, D50 are in medium level (0.15 g≤amax<0.30 g and 0.075 mm≤D50<0.425 mm), and earthquake magnitude, M is of big-sized (7≤M<8) which fits well with the engineering practice.
7 Conclusions and future work
In this paper, a hybrid approach is used to develop a BBN model for seismic soil liquefaction assessment. Five significant factors that are earthquake magnitude, mean grain size, vertical effective stress, peak ground acceleration and cone tip resistance are considered for earthquake-induced soil liquefaction potential assessment. The BBN model developed by hybrid approach showed relatively better performance than BBN model developed by ISM technique as overall performance accuracy of BBN-K2 and DK model is 97.248%, whereas that of the BBN-ISM model is 89.908%. Moreover, the hybrid approach methodology integrates the strengths of DK and K2 algorithm, and eludes the shortcomings of utilizing one method (i.e., DK or machine learning algorithms) to conclude BBN. The BBN-K2 and DK model overall classification success rate for the entire data set is compatible and promising in both instances of liquefaction and non-liquefaction with those calculated using ANN and C4.5 DT model. Moreover, the BBN model can always be updated to yield better results, as new data becomes available. The assessment of seismic soil liquefaction potential is a prime aspect of site- specific seismic hazard assessment, so accuracy is significantly important for a better model. BBN-K2 and DK model successfully identified the liquefaction occurrence with 94.286% success rate in testing phase data which is found at par with C4.5 DT and ANN models that highlighted its compatibility. Sensitivity analysis of BBN-K2 and DK model result concludes that the cone tip resistance is the most sensitive factor and earthquake magnitude is the lest sensitive factor in prediction of seismic soil liquefaction potential. The most probable explanation based on the input significant factors is that the earthquake magnitude is of big-sized, peak ground acceleration and mean grain size are in medium levels, and cone tip resistance and vertical effective stress is in small grade value, which matches well in line with engineering practice.
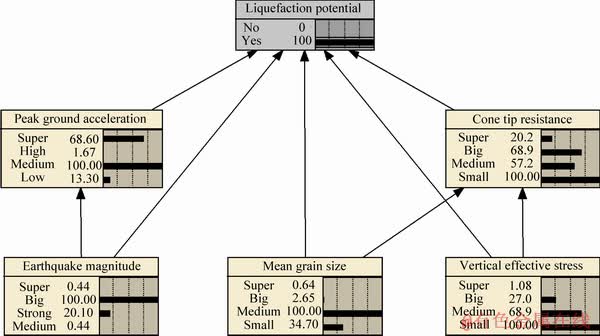
Figure 5 Most probable explanation of seismic soil liquefaction potential when evidence state is “yes”
In this study, only five significant factors of seismic soil liquefaction are considered owing to the limitation of significant factors in the case history records data and additionally more concerns are needed in the future work to quantify the uncertainties of variables involved in the directed acyclic graph based on a larger dataset. The following aspects can be considered as an extension of this work:
1) Adding more liquefaction factors such as closest distance to rupture surface, fines content, total vertical stress to expand the BBN-K2 and DK model for assessment of earthquake-induced soil liquefaction, the predictive performance is improved.
2) Adding the nodes of the utility and decision operations into the BBN model, the new model can be used as significant information for decision making in the case of expected utilities of loss.
References
[1] GOH ANTHONY T C. Seismic liquefaction potential assessed by neural networks [J]. Journal of Geotechnical Engineering, 1994, 120(9): 1467-1480. DOI: 10.1016/0148- 9062(95)99150-V.
[2] GOH ANTHONY T C. Neural-network modeling of CPT seismic liquefaction data [J]. Journal of Geotechnical Engineering, 1996, 122(1): 70-73. DOI: 10.1061/ (ASCE)0733-9410(1996)122:1(70).
[3] JUANG C H, CHEN Jin-xia, TIEN Yong-ming. Appraising cone penetration test based liquefaction resistance evaluation methods: artificial neural network approach [J]. Canadian Geotechnical Journal, 1999, 36(3): 443-454. DOI: 10.1139/t99-011.
[4] GOH ANTHONY T C, GOH S H. Support vector machines: their use in Geotechnical engineering as illustrated using seismic liquefaction data [J]. Computer and Geotechnics, 2007, 34(5): 410-421. DOI: 10.1016/j.compgeo.2007. 06.001.
[5] PAL M. Support vector machines-based modeling of seismic liquefaction potential [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(10): 983-996. DOI: 10.1002/nag.509.
[6] SAMUI P. Least square support vector machine and relevance vector machine for evaluating seismic liquefaction potential using SPT [J]. Natural Hazards, 2011, 59(2), 811-822. DOI: 10.1007/s11069-011-9797-5.
[7] SAMUI P. Seismic liquefaction potential assessment by using relevance vector machine [J]. Earthquake Engineering and Engineering Vibration, 6(4): 331-336. DOI: 10.1007/s11803-007-0766-7.
[8] ZHOU Jian, LI En-ming, WANG Ming-zheng, CHEN Xin. Feasibility of stochastic gradient boosting approach for evaluating seismic liquefaction potential based on SPT and CPT case histories [J]. Journal of Performance of Constructed Facilities, 2019, 33(3): 1-10. DOI: 10.1061/ (ASCE)CF.1943-5509.0001292.
[9] MUDULI P M, DAS S K. CPT-based seismic liquefaction potential evaluation using multi-gene genetic programming approach [J]. Indian Geotechnical Journal, 2014, 44(1): 86-93. DOI: 10.1007/s40098-013-0048-4.
[10] GANDOMI A H, ALAVI A H. Hybridizing genetic programming with orthogonal least squares for modeling of soil liquefaction [J]. International Journal of Earthquake Engineering and Hazard Mitigation, 2013, 1(1): 2-8.
[11] LIANG Wan-jie, ZHUANG Da-fang, JIANG Dong, PAN Jian-jun, REN Hong-yan. Assessment of debris flow hazards using a Bayesian network [J]. Geomorphology, 2012, 171: 94-100. DOI: 10.1016/ j.geomorph.2012.05.008.
[12] PEARL J. Probabilistic reasoning in intelligent systems [M]. San Mateo, California: Morgan Kaufmann Publishers, 1988. DOI: 10.1016/C2009-0-27609-4.
[13] COCKBURN G, TESFAMARIAM S. Earthquake disaster risk index for Canadian cities using Bayesian belief networks [J]. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 2012, 6(2): 128-140. DOI: 10.1080/17499518.2011.650147.
[14] BENSI M T, DER K A, STRAUB D. A Bayesian network framework for post-earthquake infrastructure system performance assessment [C]// Technical Council on Lifeline Earthquake Engineering Conference (TCLEE) 2009: Lifeline Earthquake Engineering in a Multihazard Environment. Oakland, CA, 2009: 1097-1107.
[15] BAYRAKTARLI Y Y, BAKER J W, FABER M H. Uncertainty treatment in earthquake modelling using Bayesian probabilistic networks [J]. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 2011, 5(1): 44-58. DOI: 10.1080/ 17499511003679931.
[16] FAIZIAN M, SCHALCHER H R, FABER M H. Consequence assessment in earthquake risk management using damage indicators [C]// First International Forum on Engineering Decision Making (IFED). Stoos, Switzerland, 2004.
[17] TESFAMARIAM S, LIU Z. Earthquake induced damage classification for reinforced concrete buildings [J]. Structural Safety, 2010, 32(2): 154-164. DOI: 10.1016/j.strusafe. 2009.10.002.
[18] BAYRAKTARLI Y Y, FABER M H. Bayesian probabilistic network approach for managing earthquake risks of cities [J]. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 2011, 5(1): 2-24. DOI: 10.1080/17499511003679907.
[19] LI Lian-fa, WANG Jin-feng, LEUNG H, JIANG Chang-sheng. Assessment of catastrophic risk using Bayesian network constructed from domain knowledge and spatial data [J]. Risk Analysis, 2010, 30(7): 1157-1175. DOI: 10.1111/j.1539-6924.2010.01429.x.
[20] SCHUBERT M, FABER M H. Common cause effects in portfolio loss estimation [J]. Structure and Infrastructure Engineering, 2011, 8(5): 497-506. DOI: 10.1080/15732479. 2010.539068.
[21] NISHIJIMA K, MAES M A, GOYET J, FABER M H. Constrained optimization of component reliabilities in complex systems [J]. Structural Safety, 2009, 31(2), 168-178. DOI: 10.1016/j.strusafe.2008.06.016.
[22] STRAUB D, KIUREGHIAN ARMEN D. Bayesian network enhanced with structural reliability methods: Methodology [J]. Journal of Engineering Mechanics, 2010, 136(10): 1248-1258. DOI: 10.1061/(ASCE)EM.1943-7889.0000173.
[23] STRAUB D, KIUREGHIAN ARMEN D. Combining Bayesian networks with structural reliability methods: application [J]. Journal of Engineering Mechanics, 2010, 136(10): 1259-1270. DOI: 10.1061/(ASCE)EM.1943-7889. 0000170.
[24] WEBER P, MEDINA-OLIVA G, SIMON C, IUNG B. Overview on Bayesian networks applications for dependability, risk analysis and maintenance areas [J]. Engineering Applications of Artificial Intelligence, 2010, 25(4): 671-682. DOI: 10.1016/j.engappai.2010.06.002.
[25] JUANG C H, JIANG Tao, ANDRUS R D. Assessing probability-based methods for liquefaction potential evaluation [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128: 580-589. DOI: 10.1061/(ASCE)1090-0241(2002)128:7(580).
[26] BAYRAKTARLI Y Y. Application of Bayesian probabilistic networks for liquefaction of soil [C]// 6th International PhD Symposium in Civil Engineering. Zurich, 2006.
[27] HUANG H W, ZHANG J, ZHANG L M. Bayesian network for characterizing model uncertainty of liquefaction potential evaluation models [J]. KSCE Journal of Civil Engineering, 2012, 16(5): 714-722. DOI: 10.1007/s12205-012-1367-1.
[28] HU Ji-lei, TANG Xiao-wei, QIU Jiang-nan. A Bayesian network approach for predicting seismic liquefaction based on interpretive structural modeling [J]. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 2015, 9(3): 200-217. DOI: 10.1080/17499518. 2015.1076570.
[29] WARFIELD J W. Developing inter connected matrices in structural modeling [J]. IEEE Transactions on Systems, Man, and Cybernetics, 1974, 4(1): 81-87.
[30] AHMAD M, TANG Xiao-wei, QIU Jiang-nan, AHMAD F. Interpretive structural modeling and MICMAC analysis for identifying and benchmarking significant factors of seismic soil liquefaction [J].Applied Sciences,2019,9(2): 233. DOI: 10.3390/app9020233.
[31] PFOHL H C, GALLUS P, THOMAS D. Interpretive structural modeling of supply chain risks [J]. International Journal of Physical Distribution & Logistics Management, 2011, 41(9): 839-859. DOI: 10.1108/09600031111175816.
[32] SAXENA J P, SUSHIL V P. Impact of indirect relationships in classification of variables–A MICMAC analysis for energy conservation [J]. Systems Research, 1990, 7(4): 245- 253. DOI: 10.1002/sres.3850070404.
[33] SUSHIL S. Interpreting the interpretive structural model [J]. Global Journal of Flexible Systems Management, 2012, 13: 87-106. DOI: 10.1007/s40171-012-0008-3.
[34] AHMAD M, TANG X W, QIU J N, AHMAD F, GU W. Application of machine learning algorithms for evaluation of seismic soil liquefaction potential [J].Frontiers of Structural and Civil Engineering.(in press)
[35] COOPER G, HERSKOVITS E. A Bayesian method for the induction of probabilistic networks from data [J]. Machine Learning, 1992, 9: 309-347. DOI: 10.1007/BF00994110.
[36] ARDAKANI A, KOHESTANI V R. Evaluation of liquefaction potential based on CPT results using C4.5 decision tree [J]. Journal of AI and Data Mining, 2015, 3(1): 85-92. DOI:10.5829/idosi.JAIDM.2015.03.01.09.
[37] ZHANG Lian-yang. Predicting seismic liquefaction potential of sands by optimum seeking method [J]. Soil Dynamics and Earthquake Engineering, 1998, 17: 219-226. DOI: 10.1016/ S0267-7261(98)00004-9.
[38] HU Ji-lei, TANG Xiao-wei, QIU Jiang-nan. Assessment of seismic liquefaction potential based on Bayesian network constructed from domain knowledge and history data [J]. Soil Dynamics and Earthquake Engineering, 2016, 89: 49-60. DOI: 10.1016/j.soildyn.2016.07.007.
[39] LI Lian-fa, WANG Jin-feng, LEUNG H, JIANG Cheng-sheng. Assessment of catastrophic risk using Bayesian network constructed from domain knowledge and spatial data [J]. Risk Analysis, 2010, 30(7): 1157-1175. DOI: 10.1111/j.1539-6924.2010.01429.x.
[40] WITTEN I H, FRANK E, HALL M A. Data mining: Practical machine learning tools and techniques [M]. Burlington, MA: Elsevier, 2011. DOI: 10.1016/ C2009-0-19715-5.
[41] WEI Jiang-tao, HUANG Du-ruo, WANG Gang. Micro-scale descriptors for particle-void distribution and jamming transition in pre- and post-liquefaction of granular soils [J]. Journal of Engineering Mechanics, 2018, 144(8): 04018067. DOI: 10.1061/ (ASCE)EM.1943-7889.0001482.
[42] WANG Gang, WEI Jiang-tao. Microstructure evolution of granular soils in cyclic mobility and post liquefaction process [J]. Granular Matter, 2016, 18: 51. DOI: 10.1007/s10035-016-0621-5.
[43] WANG Gang, XIE Yong-ning. Modified bounding surface hypoplasticity model for sands under cyclic loading [J]. Journal of Engineering Mechanics ASCE, 2014, 140(1): 91-101. DOI: 10.1061/(ASCE)EM.1943-7889.0000654.
[44] YE Jian-hong, HUANG Du-ruo, WANG Gang. Nonlinear simulation of offshore breakwater on sloping liquefied seabed [J]. Bulletin of Engineering Geology and the Environment, 2016, 75: 1215-1225. DOI: 10.1007/s10064-016-0906-2.
[45] KAVEH A, HAMZE-ZIABARI S M, BAKHSHPOORI T. Patient rule-induction method for liquefaction potential assessment based on CPT data [J].Bulletin of Engineering Geology and the Environment, 2018,77(2): 849-865. DOI: 10.1007/s10064-016-0990-3.
(Edited by ZHENG Yu-tong)
中文导读
基于贝叶斯置信网络的CPT地震液化势混合评估方法
摘要:地震液化评估是一个复杂的非线性过程,受多种因素的不确定性和复杂性的影响。贝叶斯置信网络(BBN)是一个可靠有效的工具,可以提供一个合适的框架来处理这些不确定性和因果关系。本研究采用一种混合方法来建立基于静力触探试验(CPT)案例记录数据的贝叶斯置信网络(BBN)模型,以评估土壤的地震液化势。在这种混合方法中,先通过结合领域知识(DK)的解释结构建模(ISM)技术建立朴素模型,再在K2算法中嵌入朴素模型的相关信息建立BBN-K2和DK模型。将BBN模型的结果与现有的人工神经网络(ANN)和C4.5决策树(DT)模型进行了比较和验证,发现用混合方法建立的BBN模型在液化势评估中具有良好的适应性和应用前景。用混合方法建立的BBN模型为岩土工程师评估易受地震液化影响的场地环境提供了可行的工具。最后对基于混合方法的BBN模型进行了灵敏度分析,并对液化场地进行了最可能的解释,以了解液化现象的最可能情况。
关键词:贝叶斯置信网络;静力触探;地震液化;解释结构模型;结构学习
Foundation item: Projects(2016YFE0200100, 2018YFC1505300-5.3) supported by the National Key Research & Development Plan of China; Project(51639002) supported by the Key Program of National Natural Science Foundation of China
Received date: 2019-04-29; Accepted date: 2019-12-19
Corresponding author: QIU Jiang-nan, PhD, Professor; Tel: +86-13941153942; E-mail: qiujn@dlut.edu.cn; ORCID: 0000-0001-5320- 8479
Abstract: Discernment of seismic soil liquefaction is a complex and non-linear procedure that is affected by diversified factors of uncertainties and complexity. The Bayesian belief network (BBN) is an effective tool to present a suitable framework to handle insights into such uncertainties and cause–effect relationships. The intention of this study is to use a hybrid approach methodology for the development of BBN model based on cone penetration test (CPT) case history records to evaluate seismic soil liquefaction potential. In this hybrid approach, naive model is developed initially only by an interpretive structural modeling (ISM) technique using domain knowledge (DK). Subsequently, some useful information about the naive model are embedded as DK in the K2 algorithm to develop a BBN-K2 and DK model. The results of the BBN models are compared and validated with the available artificial neural network (ANN) and C4.5 decision tree (DT) models and found that the BBN model developed by hybrid approach showed compatible and promising results for liquefaction potential assessment. The BBN model developed by hybrid approach provides a viable tool for geotechnical engineers to assess sites conditions susceptible to seismic soil liquefaction. This study also presents sensitivity analysis of the BBN model based on hybrid approach and the most probable explanation of liquefied sites, owing to know the most likely scenario of the liquefaction phenomenon.


