J. Cent. South Univ. (2017) 24: 2747-2756
DOI: https://doi.org/10.1007/s11771-017-3688-1
Texture evolution and inhomogeneous deformation of polycrystalline Cu based on crystal plasticity finite element method and particle swarm optimization algorithm
HU Li(胡励)1, 2, JIANG Shu-yong(江树勇)1, ZHANG Yan-qiu(张艳秋)1,
ZHU Xiao-ming(朱晓明)1, SUN Dong(孙冬)2
1. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China;
2. College of Materials Science and Chemical Engineering, Harbin Engineering University, Harbin 150001, China
Central South University Press and Springer-Verlag GmbH Germany,part of Springer Nature 2017
Abstract:
Texture evolution and inhomogeneous deformation of polycrystalline Cu during uniaxial compression are investigated at the grain scale by combining crystal plasticity finite element method (CPFEM) with particle swarm optimization (PSO) algorithm. The texture-based representative volume element (TBRVE) is used in the crystal plasticity finite element model, where a given number of crystallographic orientations are obtained by means of discretizing the orientation distribution function (ODF) based on electron backscattered diffraction (EBSD) experiment data. Three-dimensional grains with different morphologies are generated on the basis of Voronoi tessellation. The PSO algorithm plays a significant role in identifying the material parameters and saving computational time. The macroscopic stress–strain curve is predicted based on CPFEM, where the simulation results are in good agreement with the experimental ones. Therefore, CPFEM is a powerful candidate for capturing the texture evolution and clarifying the inhomogeneous plastic deformation of polycrystalline Cu. The simulation results indicate that the <110> fiber texture is generated finally with the progression of plastic deformation. The inhomogeneous distribution of rotation angles lays the foundation for the inhomogeneous deformation of polycrystalline Cu in terms of grain scale.
Key words:
plastic deformation; crystal plasticity; finite element method; texture evolution；
1 Introduction
Most of metal alloys that are commonly used in the engineering field belong to polycrystals, which can be viewed as an aggregation of single crystal with specific orientation. In general, when the metal polycrystals are subjected to plastic deformation, the randomly distributed grains exhibit the preferential orientation. As a consequence, the deformation texture is induced and it leads to the anisotropy of metal polycrystals. However, macroscale finite element method based on conventional plastic deformation theory is unable to capture the anisotropy of metal polycrystals. Therefore, crystal plasticity finite element method (CPFEM) becomes a candidate for predicting the texture evolution of polycrystalline metals [1]. On the one hand, CPFEM is capable of employing various plastic flow and hardening rules. On the other hand, CPFEM is able to provide the flexibility of handling complex internal or external boundary conditions. In particular, CPFEM has developed into an extremely versatile tool for describing the mechanical response of crystalline materials in terms of all length scales, such as macroscale, mesoscale and microscale [2–4].
The parameter calibration of crystal plasticity model plays an indispensable role in grasping the meaningful information of texture evolution and polycrystalline deformation during crystal plasticity finite element simulation [5]. In general, the crystal plasticity parameters for polycrystalline metals would be calibrated by using microscale tests, but it is fairly difficult to conduct such mechanical tests at the microscale. Conventionally, the crystal plasticity parameters in the single-crystal constitutive equation, which are used for polycrystal deformation analysis, are almost universally calibrated by simultaneous fitting the stress–strain curves obtained from tension/compression test in the loading direction to numerical results [6]. Such calibration is a nontrivial effort due to the complexity of the model as well as the number of parameters involved. Based on the aforementioned difficulties, the ‘trial-error’ method has been a dominant one in the procedure of calibrating the constitutive parameters. It is worth mentioning that a “trial-error” procedure is generally time consuming but its results with respect to parameter identification are not as “improper” as the term might indicate [7]. Systematic variations of parameters require a phenomenological interpretation and an understanding of the respective efforts on the mechanical response of the structure. Due to the aforementioned limitation of the ‘trial-error’ method, some various approaches have been adopted to facilitate the procedure for parameter identification. ABDOLVAND et al [8] firstly optimized the agreement between the self-consistent model and the experimental results, and then they adjusted the parameters obtained from self-consistent model in oder to finally calibrate the parameters used for crystal plasticity finite element simulation. This parameter calibration procedure, in a way, is also similar to a ‘trial-error’ method but with a set of better initial values. HASIJA et al [9] used a continuous function optimization method to minimize the difference between experiments and model predictions for the set of design variables. This method has a more mathematical meaning, but it is also difficult to operate with the increase in the number of material parameters which need to be identified. In addition, the genetic algorithm (GA) technique of discrete function minimization is introduced into parameter identification procedure, which not only reduces the computation time, but also enables automation of parameter calibration [10, 11].
Compared to genetic algorithm, on the one hand, particle swarm optimization (PSO) algorithm does not have crossover and mutation operators and thus makes implementation easier. On the other hand, PSO algorithm likewise has the characteristic of high precision and fast convergence [12]. To our knowledge, the procedure of calibrating the constitutive parameters based on PSO algorithm has not yet been reported in the literature. Therefore, in the present study, a minimization procedure based on PSO algorithm is used to calibrate the parameters of crystal plasticity constitutive model in consideration of the backstress effect. The results show that the procedure not only reduces the threshold and computation time of parameter identification for 5 or more parameters, but also guarantees computational accuracy of the crystal plasticity finite element simulation.
2 Materials and methods
2.1 Material characterization
The experimental material used in the present study was the commercial pure copper (Cu) bar, which was fabricated by means of rolling. The samples with the diameter of 4 mm and the height of 6 mm were cut from the as-received Cu bar by means of electro-discharge machining (EDM) in order to be used for uniaxial compression experiments. The Cu samples were placed between the top anvil and the bottom one of the INSTRON equipment and then were compressed to the deformation degree of 60% at the strain rate of 0.001 s–1 at room temperature. The perfect lubrication was performed between the as-received Cu sample and the anvils.
To acquire the grain morphology and crystallographic orientation of as-received Cu, electron backscattered diffraction (EBSD) experiments were conducted on the material using a Zeiss Supra 55 scanning electron microscope (SME) coupled with OXFORD EBSD instrument. Due to the relatively large grain size, the scan step was chosen to be 1.5 μm. In order to obtain the three-dimensional profile of the grain shape, two cross-sections of the cylinder specimen, i.e. the rolling direction and normal direction (RD-ND) and transverse direction and normal direction (TD-ND) sections were scanned and the results are shown in Fig. 1. The grain size of as-received Cu can be determined as 30 μm×20 μm×25 μm.
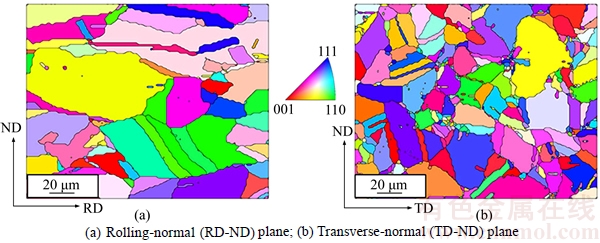
Fig. 1 Initial microstructure of as-received Cu described by inverse pole figures in different sections:
2.2 Establishment of texture-based RVE model
Most of the commonly available alloys are polycrystals which contain millions of grains in a standard test specimen. Although the computational efficiency of computers has been increased tremendously, it is still a challenge to simulate the response of bulk material with millions of grains. Therefore, the concept of representative volume element (RVE) model naturally emerges, and it has been widely discussed and implemented in the microscale simulation [13]. The key purpose of the RVE model is to statistically represent the global response of macroscale material behavior by using a sufficient number of grains. In addition, the RVE approach is capable of accounting for equilibrium and compatibility in a microscopically heterogeneous structure. As a result, the RVE approach is able to build the bridge between simulations based on different length scales on the basis of acceptable accuracy and computational time cost.
Since it can be assumed that deformation is highly sensitive to the overall texture, it is important to assign appropriate crystallographic orientations to the elements prior to finite element simulation. In the conventional RVE, the crystallographic orientations are directly obtained from EBSD data. However, this method of orientation selection from EBSD data is statistically difficult and it is unable to guarantee the representation of initial texture by using the volume-weighted selection. To further improve the normal RVE method, we used the texture-based RVE (TBRVE) model in which a given number of crystallographic orientations are obtained by following the method of discretizing the orientation distribution function (ODF) [14]. The used TBRVE model represents both the grain morphology and the texture which are the two major sources of crystalline anisotropy. The main process of orientation discretization and assignment is shown in Fig. 2. The detailed process and the related theory can be obtained in Ref. [14], which would be not discussed here.
In the present study, 729 grain orientations are extracted from the EBSD data by discretizing ODF, and the convergence study of orientations in the TBRVE indicates that 729 orientations are sufficient for representing the basic characteristics of initial texture and give a balance between the number of discrete orientations and computational efficiency. As can be seen in Fig. 2(d), the TBRVE model consists of 8924 C3D8 elements and each grain is composed of many elements with the same orientation. The grain size in the TBRVE is to be around 30 μm×20 μm×25 μm, which is similar to the grain dimensions observed from the EBSD scans performed on the as-received Cu of interest here.
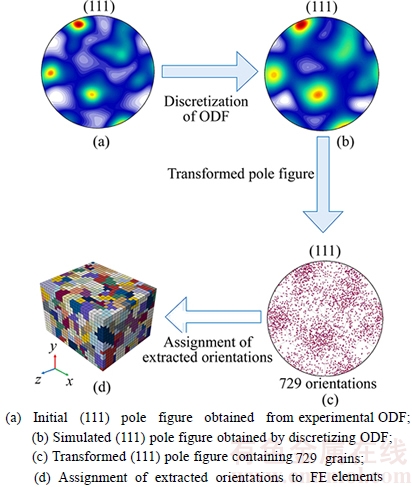
Fig. 2 Main process of orientation discretization and orientation assignment:
2.3 Applied boundary conditions
Plastic deformation at the grain scale can be potentially affected by boundary conditions (BCs) since boundaries can show stress concentrations associated with the applied constrains. To minimize the effects of boundary assumption, the period boundary condition (PBC) [8] has been adopted in the current study. It is assumed that PBC can represent the interaction between RVE and surrounding grains more realistically. Moreover, the use of PBC requires the application of equations on the surface nodes of the model elements and thus makes the block of model elements represent a ‘unit cell’. These equations indicate that the opposite surfaces deform in the same manner, which results in a continuum of deformation between cells. For instance, the following constraints are imposed on the surface ABCD and EFGH in Fig. 3:
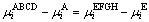(i=x, y, z) (1)
where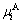 
and 
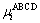are the displacements in the directions (x, y, z) of corner A and surface ABCD, respectively. Similar constrains are imposed on the four other surfaces. In Fig. 3, corner E is fixed in all the directions and the three master nodes are A, F and H. Corner A is fixed in x and y directions, but it can move freely in z direction. In other words, displacement for tension/compression along ND can be applied at this point. Similarly, corner F is fixed in y and z directions, but it can move with freedom in x direction and corner H is fixed in x and z directions, but is free to move in y direction, so loading along RD and TD can be applied at point F and H, respectively.
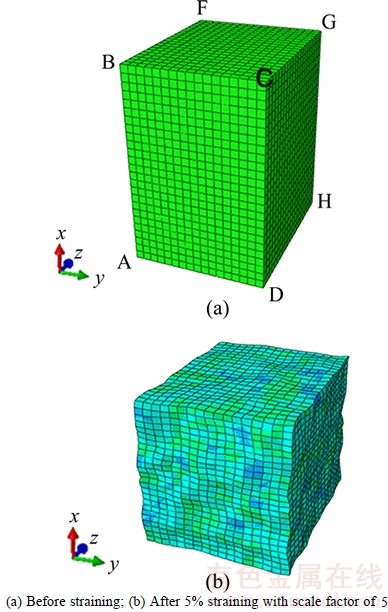
Fig. 3 Configurations of TBRVE model under various conditions of compressive deformation along x direction:
2.4 Crystal plasticity constitutive model
It is worth mentioning that with the progression of plastic deformation, the deformed polycrystalline Cu specimens notably with high stacking fault energy exhibit formation of microstructures characterized by dislocation cell blocks (CBs) which have relatively low dislocation density inside the cell and are separated by high dislocation density on the CB boundaries [15, 16]. These high dislocation density regions behave elastically and give rise to internal stress, which is defined as backstress. The most significant effect of backstress is the selective increase in activity on some slip systems and the reduction of slip system activity on certain slip systems. Meanwhile, backstress also has an impact on the texture evolution of polycrystalline aggregate [17]. Therefore, in the present study, the backstress is incorporated into crystal plasticity model in order to capture the heterogeneous plastic deformation and the texture evolution of polycrystalline Cu.
ROTERS et al [18] have comprehensively reviewed various crystal plasticity models incorporated in FEM that have been developed over the past decades. The framework of the current code was initially developed by HUANG [19] to capture plastic deformation for dislocation in FCC polycrystals. In the present work, the backstress is implemented within the elasto-viscoplastic model of crystal and the corresponding key equations of crystal plasticity constitutive model are summarized as follows.
In the framework of crystal plasticity theory [20, 21], a crystalline material is embedded on its lattice, whereas the lattice itself undergoes elastic deformation and rotation. The inelastic deformation of a single crystal is assumed here to arise solely by virtue of dislocation motion. Then the total deformation gradient F can be expressed as a multiplicative decomposition into the elastic and plastic components as shown in Eq. 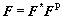(2).
(2)
where FP is plastic deformation gradient, which represents the crystallographic slip along slip plane, and F* is the elastic deformation gradient incorporating the elastic stretch and rigid body rotation of the configuration.
From the definition of velocity gradient L in the current state, it can be expressed as
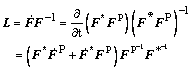
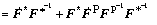
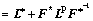(3)
where
which stands for the plastic deformation velocity gradient in the intermediate configuration.
Furthermore, the plastic deformation velocity gradient can be determined as the sum of the slipping shear rate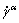 
in the individual α slip system according to the following equation:
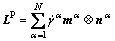(4)
where N is the total number of slip system; mα and nα are the unit vectors which stand for the slip direction and the normal to the slip plane in the intermediate configuration, respectively and operator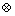 
is the dyadic product of two vectors.
The backstress on the α-slip systems,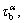
is incorporated in a widely used empirical power law of the flow rule to reflect the backstress effect [22, 23]:
(5)
In the above formulation, the rate dependency can be controlled by strain rate sensitivity exponent m. If the material is rate-independent, a large value of m can be chosen up to 50, whereas if the material is highly rate-dependent, a typical value of 10 with respect to m can be used.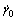 
is a reference shear strain rate. τα and gα are resolved shear stress and the slip resistance on the α-slip system, respectively.
The rate of change of slip resistance in each slip is given as follows:
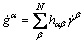(6)
where hαβ is the slip hardening modulus, and the sum operation is performed over all the activated slip systems. Here, hαα is known as self-hardening modulus and it is derived from the hardening of slip system itself. In addition, hαβ (α≠β) is called latent-hardening modulus which indicates the hardening caused by another slip system.
Furthermore, the hardening model is given by [24]
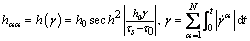
(7)
where h0 is the initial hardening modulus; τ0 is the initial yield stress; τs is the saturation stress; γ is the total shear strain in all the slip systems; and q is the ratio of latent-hardening modulus to self -hardening modulus and its value generally ranges from 1.0 to 1.4.
The evolution of backstress on the individual slip system is introduced as follows [14]:
(8)
where c and d are the material parameters.
The crystallographic formulations were implemented numerically into the finite element (FE) code ABAQUS within the framework of large strain kinematics via a user-defined material subroutine (UMAT), where the implicit (Euler backward) integration algorithm was adopted [19].
2.5 Determination of material parameters for simulation
It is very critical to systematically calibrate the material parameters according to the experimental results in order to obtain a meaningful simulation of deformation process for the crystalline materials. Though the material parameters of the proposed crystal plasticity model can be calibrated by simultaneous fitting the simulated stress–strain curves to experimental results, such calibration is a nontrivial effort due to the complexity of the model as well as the number of parameters involved. In the present study, the constitutive parameters to be calibrated in the FCC Cu include the following sets: (a) The set Xel=[C11, C12, C44] of three anisotropic elastic stiffness components; (b) The set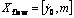 
of flow-related parameters; (c) The set 
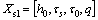of the self-hardening and latent- hardening parameters; (d) The set 
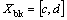of the backstress-related parameters.
Anisotropic stiffness constants were first determined from Ref. [19]. The constants were taken as C11=168.4 GPa, C12=121.4 GPa and C44=75.4 GPa. The crystal plasticity model was then calibrated by fitting the stress–strain response of polycrystalline Cu subjected to uniaxial compression by deformation degree of 20% along x direction at the strain rare of 0.001 s–1. Prior to the corresponding fitting, some material parameters in the sets Xflow and Xsl, namely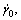 
m, q, can be determined without calculation. As a reference shear strain rate, 
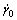is determined as 0.001 s–1, which is proper for quasi-static loading rate. Moreover, the value of m is chosen as 10, which is the same as that for OFHC Cu single crystal [19]. In addition, parameter q is chosen as 1, which is attibuted to the fact that hardening from dislocation slip is considered to be the same for all slip systems.
In order to verify the parameter identification, according to Ref. [10], an error function is defined as follows:
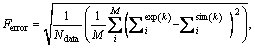
k=1, 2, …, 40 (9)
where k is a number denoting the amplitude of 40 different true strains which range form 0.001 to 0.2 with the interval of 0.005. In addition, M indicates the number of experimental curves and is set to be 1 within this study. Ndata stands for the total number of data points.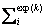
and 
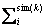are the stresses measured in the experimental and simulated stress–strain curves for kth strain amplitude, respectively.The PSO technique of discrete function minimization is implemented for the purpose of determining the material parameters. The particle swarm is a population-based stochastic algorithm for optimization which is based on the principles of social psychology [12]. Unlike evolutionary algorithms like the GA, the PSO algorithm does not use selection. In general, all population members survive from the beginning of a trial until the end. Their interactions result in iterative improvement of the quality of problem solutions over time. The procedure is repeated by tracking the personal Best (pBest) and global Best (gBest) in each iteration. A common practice to stop the iteration is to fix the number of trials in which no further improvement in the value of objective function takes place. Compared to the GA, the PSO does not have crossover and mutation operation and does not need to be coded into a binary equivalent string of 0’s and 1’s which is called a chromosome. According to the abovementioned advantages, PSO algorithm is easy to realize and does not have many parameters to adjust.
In what follows, the crystal plasticity finite element model has been interfaced with PSO technique to find the material parameters of as-received Cu. This method is generally composed of an optimization tool, a material model and an interface. The procedure is described in Fig. 4. Thirty simulations are done for each generation while the population size is taken to be 5, which indicates that there are five material parameters to be determined. In Fig. 4, each particle swarm refers to a set of material parameters (h0, τs, τ0, c, d), so the global stress–strain curve can be obtained by performing the crystal plasticity finite element simulation using the corresponding set of material parameters. Using Eq. (9) as a fitness function, the error between the numerical and the experimental results can be calculated, and thus the personal Best (pBest) and global Best (gBest) in each iteration of PSO algorithm can be determined, which would be used for the update of individual particle swarms in each iteration. Finally, when the requirement of convergence is achieved, the optimal material parameters can be determined.
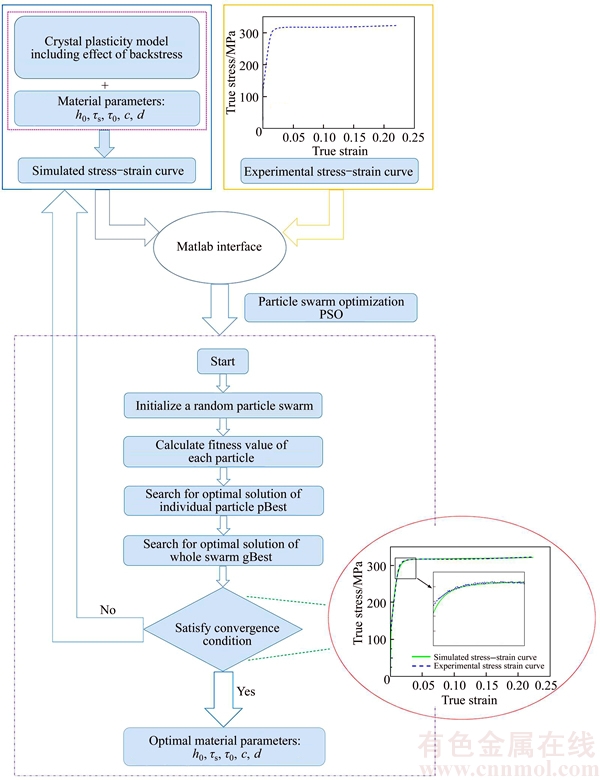
Fig. 4 Flow chart of parameter determination
Figure 5(a) shows the PSO convergence rate for minimization of a chosen fitness function with the number of generations. Material parameters obtained by this calibration process are listed in Table 1. Excellent match is obtained between the experimental stress–strain curve for uniaxial compression and simulated stress– strain one at the strain rate of 0.001 s–1 by using the calibrated parameters, as shown in Fig. 5(b). The results indicate that the adopted crystal plasticity finite element model can give a precise prediction of the uniaxial compression deformation behavior of as-received Cu.
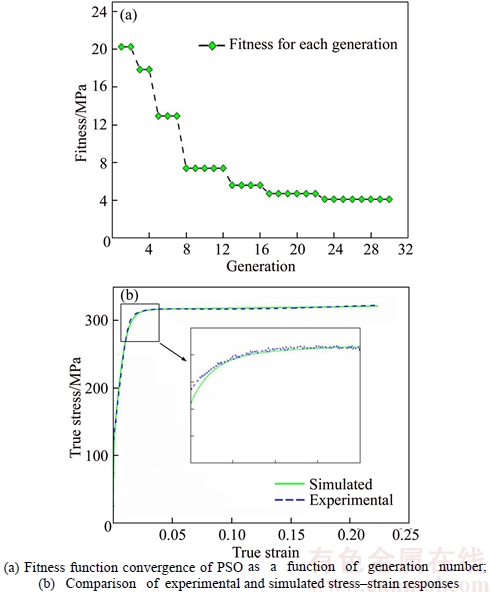
Fig. 5 Convergence of PSO algorithm in aspect of parameter calibration and validity of material parameters using methodology of coupling crystal plasticity finite element model and PSO technology:
3 Results and discussion
3.1 Texture evolution during uniaxial compressive deformation
Figure 6 shows the pole figures of as-received Cu subjected to compression deformation degree of 60%, which are obtained on the basis of EBSD experiment and CPFEM simulation, respectively. It can be found that the experimental results are in good agreement with the simulated ones, which indicates that CPFEM plays a significant role in predicting the texture evolution of polycrystalline Cu sample during plastic deformation.
According to the established crystal plastic finite element model, the texture evolution of polycrystalline Cu during uniaxial compression is simulated in the case of various deformation degrees, which is demonstrated in Fig. 7, where the inverse pole figures are given. It can be found from Fig. 7 that as for the as-received Cu, <110> fiber texture is rather weak. With the progression of plastic deformation, a crystallographic plane of individual grain in the polycrystalline Cu gradually rotates to be perpendicular to the compression direction. As a consequence, the <110> fiber texture is generated finally. It can be concluded that the used crystal plastic finite element model can not only predict the macroscopic tress-strain curve, but also simulate the texture evolution of as-received Cu during uniaxial compression deformation.
3.2 Inhomogeneous plastic deformation during uniaxial compression
To further analyze the inhomogeneous plastic deformation of polycrystalline Cu during uniaxial compression, the rotation angle α about specific rotation axes [h k l] is adopted according to the following expression [25]:
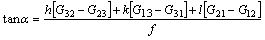(10)
where G is an arbitrary rotation tensor and h, k, l are the axes indexes adopted under the global coordinate system. In the present study, the adopted rotation axes are along RD, TD and ND, which correspond to [100], [010] and [001] directions, respectively. Furthermore, f can be expressed as follows:
Table 1 Material parameters of as-received Cu for crystal plasticity finite element simulation
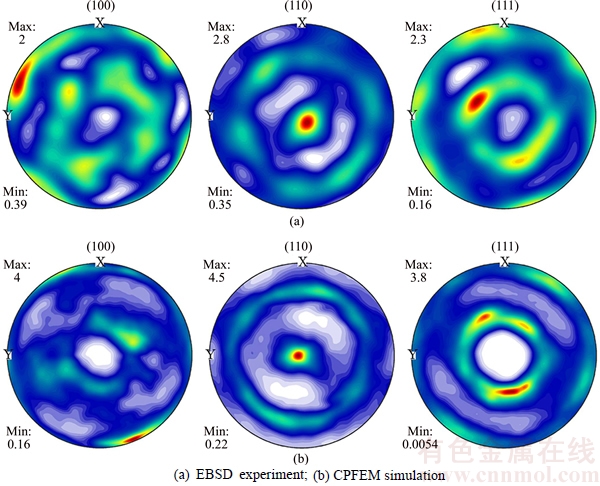
Fig. 6 Pole figures of as-received Cu subjected to uniaxial compression at deformation degree of 60%:
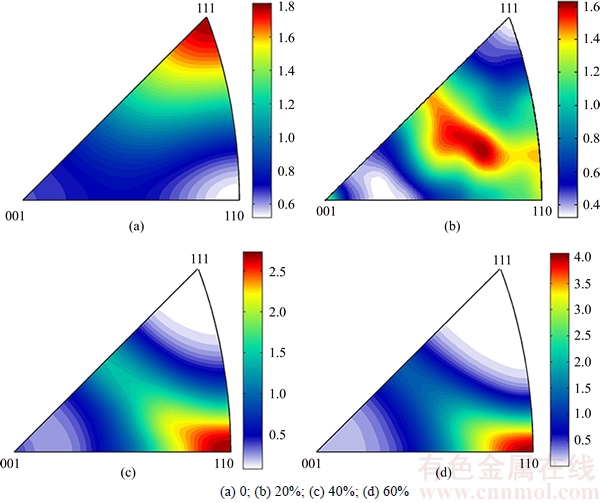
Fig. 7 Evolution of inverse pole figures of crystal plastic finite element simulation corresponding to as-received Cu at various deformation degrees:
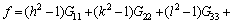
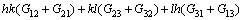(11)
Distribution of rotation angles with respect to [100], [010], and [001] directions in each integration point at the deformation degree of 60% are statistically analyzed in Fig. 8. It can been seen from Fig. 8 that the rotation angles along three specific axes mainly range from –75° to 75°. In addition, these rotation angles have almost the same statistical distribution, where the standard deviations of the aforementioned rotation angels about [100], [010], and [001] directions only have a slight difference.
Figure 9 shows the distribution of rotation angle and strain of polycrystalline Cu at the deformation degree of 60%. It can be seen from Fig. 9 that the individual grain rotates around [100], [010] and [001] directions during plastic deformation, which contributes to the compatible deformation among the grains and in the grain interior. Moreover, since there is the orientation difference among the initial grains in the as-received Cu, dislocation slip in the individual grain exhibits a certain difference, which leads to an inhomogeneous distribution of rotation angles. As a consequence, the inhomogeneous distribution of rotation angles plays a significant role in the inhomogeneous deformation of polycrystalline Cu in terms of grain scale.
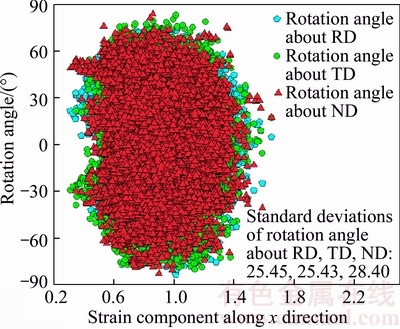
Fig. 8 Statistical analysis of rotation angles in each integration point at deformation degree of 60%
4 Conclusions
1) Combining CPFEM with PSO algorithm contributes to investigating texture evolution and inhomogeneous deformation of polycrystalline Cu during uniaxial compression. The PSO algorithm plays a significant role in identifying the material parameters and saving computational time.
2) The macroscopic stress–strain curve is predicted based on CPFEM, where the simulation results are in good agreement with the experimental ones. The crystal plasticity finite element simulation results indicate that the <110> fiber texture is generated finally with the progression of plastic deformation. The inhomogeneous distribution of rotation angles lays the foundation for the inhomogeneous deformation of polycrystalline Cu in terms of grain scale.
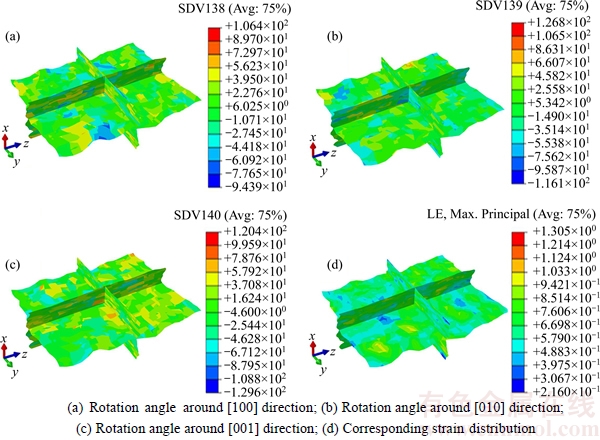
Fig. 9 Distribution of rotation angle (degree) and strain of polycrystalline Cu at deformation degree of 60%:
References
[1] MAO Liu, TIEU A K, CHENG Lu, ZHU Hong-tao, DENG Guan-yu. A crystal plasticity study of the effect of friction on the evolution of texture and mechanical behaviour in the nano-indentation of an aluminium single crystal [J]. Computational Materials Science, 2014, 81: 30–38.
[2] ARDELJAN M, BEYERLEIN I J, MCWILLIAMS B A, KNEZEVIC M. Strain rate and temperature sensitive multi-level crystal plasticity model for large plastic deformation behavior: Application to AZ31 magnesium alloy [J]. International Journal of Plasticity, 2016, 83: 90–109.
[3] SEGURADO J, LLORCA J. Simulation of the deformation of polycrystalline nanostructured Ti by computational homogenization [J]. Computational Materials Science, 2013, 76: 3–11.
[4] ZHANG Jing, CHEN Zhang-hua, DONG Chao-Fang. Simulating intergranular stress corrosion cracking in AZ31 using three-dimensional cohesive elements for grain structure [J]. Journal of Materials Engineering and Performance, 2015, 24(12): 4908–4918.
[5] LI Ling, SHEN Lu-ming, PROUST G, MOY C K S, RANZI G. Three-dimensional crystal plasticity finite element simulation of nanoindentation on aluminium alloy 2024 [J]. Materials Science and Engineering A, 2013, 579: 41–49.
[6] LEE M G, LIM H, ADAMS B L, HIRTH J P, WAGONER R H. A dislocation density-based single crystal constitutive equation [J]. International Journal of Plasticity, 2010, 26(7): 925–938.
[7] ZHANG Ke-shi, JU J W, LI Zhen-huan, BAI Yi-long, BROCKS W. Micromechanics based fatigue life prediction of a polycrystalline metal applying crystal plasticity [J]. Mechanics of Materials, 2015, 85: 16–37.
[8] ABDOLVAND H, DAYMOND M R, MAREAU C. Incorporation of twinning into a crystal plasticity finite element model: evolution of lattice strains and texture in Zircaloy-2 [J]. International Journal of Plasticity, 2011, 27(11): 1721–1738.
[9] HASIJA V, GHOSH S, MILLS M J, JOSEPH D S. Deformation and creep modeling in polycrystalline Ti–6Al alloys [J]. Acta Materialia, 2003, 51(15): 4533–4549.
[10] XIE C L, GHOSH S, GROEBER M. Modeling cyclic deformation of HSLA steels using crystal plasticity [J]. Journal of Engineering Materials and Technology, 2004, 126(4): 339–352.
[11] CHENG Jia-hao, GHOSH S. A crystal plasticity FE model for deformation with twin nucleation in magnesium alloys [J]. International Journal of Plasticity, 2015, 67: 148–170.
[12] ESMIN A A A, COELHO R A, MATWIN S. A review on particle swarm optimization algorithm and its variants to clustering high-dimensional data [J]. Artificial Intelligence Review, 2015, 44(1): 23–45.
[13] DIARD O, LECLERCQ S, ROUSSELIER G, GAILLETAUD G. Evaluation of finite element based analysis of 3D multicrystalline aggregates plasticity: Application to crystal plasticity model identification and the study of stress and strain fields near grain boundaries [J]. International Journal of Plasticity, 2005, 21(4): 691–722.
[14] LI Ling, SHEN Lu-ming, PROUST G. A texture-based representative volume element crystal plasticity model for predicting Bauschinger effect during cyclic loading [J]. Materials Science and Engineering A, 2014, 608: 174–183.
[15] MA A, ROTERS F. A constitutive model for fcc single crystals based on dislocation densities and its application to uniaxial compression of aluminium single crystals [J]. Acta Materialia, 2004, 52(12): 3603–3612.
[16] HUANG Xiao-xu, WINTHER G. Dislocation structures. Part I. Grain orientation dependence [J]. Philosophical Magazine, 2007, 87(33): 5189–5214.
[17] BRAHME A P, INAL K, MISHRA R K, SAIMOTO S. The backstress effect of evolving deformation boundaries in FCC polycrystals [J]. International Journal of Plasticity, 2011, 27(8): 1252–1266.
[18] ROTERS F, EISENLOHR P, HANTCHERLI L, TJAHJANTO D D, BIELER T R, RAABE D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications [J]. Acta Materialia, 2010, 58(4): 1152–1211.
[19] HUANG Yong-gang. A user-material subroutine incroporating single crystal plasticity in the ABAQUS finite element program [M]. Cambridge Massachusetts, USA: Harvard University, 1991: 1–21.
[20] HILL R, RICE J R. Constitutive analysis of elastic-plastic crystals at arbitrary strain [J]. Journal of the Mechanics and Physics of Solids, 1972, 20(6): 401–413.
[21] ASARO R J, RICE J R. Strain localization in ductile single crystals [J]. Journal of the Mechanics and Physics of Solids, 1977, 25(5): 309–338.
[22] CAILLETAUD G. A micromechanical approach to inelastic behaviour of metals [J]. International Journal of Plasticity, 1992, 8(1): 55–73.
[23] LU Feng, ZHANG Guang, ZHANG Ke-shi. Discussion of cyclic plasticity and viscoplasticity of single crystal nickel-based superalloy in large strain analysis: comparison of anisotropic macroscopic model and crystallographic model [J]. International Journal of Mechanical Sciences, 2004, 46(8): 1157–1171.
[24] PEIRCE D, ASARO R J, NEEDLEMAN A. An analysis of nonuniform and localized deformation in ductile single crystals [J]. Acta Metallurgica, 1982, 30(6): 1087–1119.
[25] WERT J A, LIU Q, HANSEN N. Dislocation boundary formation in a cold-rolled cube-oriented Al single crystal [J]. Acta Materialia, 1997, 45(6): 2565–2576.
(Edited by YANG Hua)
Cite this article as:
HU Li, JIANG Shu-yong, ZHANG Yan-qiu, ZHU Xiao-ming, SUN Dong. Texture evolution and inhomogeneous deformation of polycrystalline Cu based on crystal plasticity finite element method and particle swarm optimization algorithm [J]. Journal of Central South University, 2017, 24(12): 2747–2756.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-017-3688-1Foundation item: Projects(51305091, 51475101) supported by the National Natural Science Foundation of China; Project(20132304120025) supported by Specialized Research Fund for the Doctoral Program of Higher Education, China
Received date: 2016-08-23; Accepted date: 2016-11-03
Corresponding author: JIANG Shu-yong, PhD, Professor; Tel: +86–13936266338; E-mail: jiangshy@sina.com
Abstract: Texture evolution and inhomogeneous deformation of polycrystalline Cu during uniaxial compression are investigated at the grain scale by combining crystal plasticity finite element method (CPFEM) with particle swarm optimization (PSO) algorithm. The texture-based representative volume element (TBRVE) is used in the crystal plasticity finite element model, where a given number of crystallographic orientations are obtained by means of discretizing the orientation distribution function (ODF) based on electron backscattered diffraction (EBSD) experiment data. Three-dimensional grains with different morphologies are generated on the basis of Voronoi tessellation. The PSO algorithm plays a significant role in identifying the material parameters and saving computational time. The macroscopic stress–strain curve is predicted based on CPFEM, where the simulation results are in good agreement with the experimental ones. Therefore, CPFEM is a powerful candidate for capturing the texture evolution and clarifying the inhomogeneous plastic deformation of polycrystalline Cu. The simulation results indicate that the <110> fiber texture is generated finally with the progression of plastic deformation. The inhomogeneous distribution of rotation angles lays the foundation for the inhomogeneous deformation of polycrystalline Cu in terms of grain scale.
