Article ID: 1003-6326(2005)06-1328-05
Modeling of effects of matrix on actuation characteristics of embedded shape memory alloy wires
CUI Xiao-long(崔晓龙)1, ZHENG Yan-jun(郑雁军)2, CUI Li-shan(崔立山)2
(1. Technology Center, Shenzhen Fiyta Holdings LTD, Shenzhen 518057, China;
2. Department of Materials Science and Engineering, University of Petroleum,
Beijing 102249, China)
Abstract:
Effects of matrix properties on the actuation characteristics of embedded shape memory alloy wires were studied. The coefficient of thermal expansion and the modulus of matrix have significant effect on the maximum recovery stress. The thermal strain rate of the SMA wires upon heating is more sensitive to the matrix properties than the stress rate does. Additional fibers embedded in the matrix have significant effect on the stress distribution between the SMA wires and the matrix, and thus affect the interface quality significantly. Fibers with negative thermal expansion coefficient are beneficial to the interface between shape memory alloy wires and the epoxy matrix. All conclusions based on the numerical modeling can find experimental supports.
Key words:
shape memory alloys; composite; actuation; matrix CLC;
number: TB381 Document code: A
1 INTRODUCTION
One major application field of shape memory alloys(SMAs) is the so-called smart structures. Numerous researches have been done on the actuation abilities of SMAs, and the results are quite inspiring[1, 2]. However, the complicated behaviors of SMAs are still not fully understood, which prevents SMAs from being further adopted in real industrial structures. The difficulties in understanding the SMAs mainly come from the fact that the transformation and thus the actuation abilities of SMAs are affected by quite a lot factors, such as chemical composition[3], thermo-mechanical treatment history[4], deformation[5] and external constraining conditions[6, 7].
Our previous researches concerning the effects of constraining conditions on the actuation behaviors of SMAs have shown that SMAs reinforced composites have quite different actuation behaviors with different matrices[6]. Analysis revealed that the constraining failure (e.g. the interface failure in SMAs composites) was an important mechanism that changes the actuation behaviors of SMAs[8, 9]. For smart structures with perfect constraining, the coefficient of thermal expansion(CTE) and the stiffness of the constraining media were thought as the main parameters in affecting the actuating abilities of SMAs. However, the obtained results are controversial[10, 11], and there are no satisfying numerical interpretations up to now. In this paper, a thermodynamic model developed based on experimental results was developed, and the effects of external constraining conditions on the actuation abilities of SMAs were numerically analyzed.
2 MATHEMATICAL MODELING
Although none of the models developed so far is globally satisfying, a common understanding has been achieved that a successful modeling should be constructed on the basis of clearly defined physical parameters. Therefore, phenomenological modeling is still receiving a great deal of attention. Analysis has shown that a satisfying model lays heavily on the adopted kinetic equations of thermoelastic martensitic transformation[12]. A generalized thermodynamic model has been developed based on experimental results to predict the thermomechanical behavior of SMAs[13]. The yielded equation for the forward martensitic transformation is given by
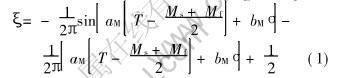
The reverse martensitic transformation is given by
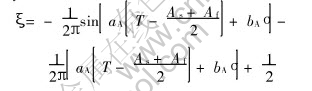 (2)
(2)
where ξ is the martensite fraction, Ms, Mf, As and Af are the martensitic transformation starting and finishing temperature, reverse transformation starting and finishing temperature, respectively. The four material constants aM, bM, aA and bA are selected as

where CM and CA are the stress-temperature coefficient for Ms and As, respectively.
For SMAs embedded in structures, the constitutive equation for the materials is selected to be the simple equation as
σ=E ε(4)
Eqn.(4) has already been validated by numerous experiments and thus ensures a well-founded basis for our modeling. The stress of the whole structure is expressed by the stress of SMA (σSMA) and the constraining matrix (σM) on the bases of the rule of mixture, as
σ=φSMAσSMA+(1-φSMA)σM(5)
where φSMA is the volume fraction of SMA. Similarly, the modulus of the composite, and the modulus of SMA (a combination of the modulus of martensite and the parent phase, EMA and Ep) can be expressed as
![]()
The boundary conditions for the model is
εtrSMA+εelSMA+αSMAΔT=εelm+αmΔT(7)
where subscript m denotes the constraining matrix; superscript tr denotes the transformation strain; superscript el denotes the elastic strain; α denotes the coefficient of thermal expansion.
Eqns.(1) to (7) construct the bases of the modeling in this paper. The equations are incorporated into a computer program and solved using the Euler method. Important parameters used in simulation are summarized in Table 1[9].
Table 1 SMA parameters used in calculation[9]

3 SIMULATION
3.1 Effects of matrix expansion on actuation characteristics
One can see from Fig.1(a) that the CTE of the matrix limits the maximum recovery stress of the embedded SMA wires. As can be seen, a CTE value -0.0005 (meaning the matrix contracts upon heating) of the matrix limits the recovery stress of SMA to about 370MPa. For a positive CTE value of 0.00005, the recovery stress does not reach its maximum value within the temperature range, indicating that the reverse martensitic transformation has not finished yet. Theoretically, results in Fig.1(a) may be regarded as a design principle of SMA devices if the maximum output stress is concerned. For example, the maximum recovery stress value of the SMA in a Kevlar/epoxy composite should be less than an equivalent SMA embedded in a glass fiber/epoxy composite, since the Kevlar fiber/epoxy composite has a smaller CTE than the glass fiber/epoxy composite.
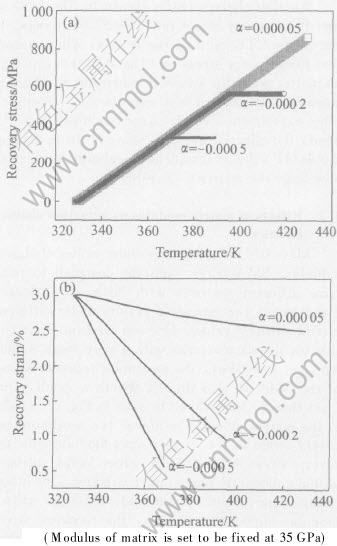
Fig.1 Effects of matrix dilatation on recovery stress(a) and recovery strain(b) of embedded SMA wires
In practice, however, the interface of a SMA composite may fail before the recovery stress reaches its maximum value[8, 9]. Furthermore, the CTE values of materials in reality usually fall into the magnitude range of several decade millionth. From Fig.1(a) one can learn that such a small CTE value will not exert significant influence on the maximum recovery stress. Thus, the effect of the CTE value of the constraining matrix on the maximum recovery stress is negligible, except that extremely large CTE value (whichever negative or positive) is involved.
One the other hand, it can be seen from Fig.1(b) that the shape of the SMA composite varies significantly with different matrix CTE. It seems that the strain of the SMA elements is more sensitive to the matrix properties than the stress does. Our previous experimental results show that the strain-temperature behaviors of SMA composites are more sensitive to materials properties than the stress-temperature and stress-strain behaviors do[14], which can be regarded as an experimental proof of Fig.1.
Another characteristics shown in Fig.1(a) is that the recovery stress rate (dσ/dT) is independent on the CTE value of the matrix, which means that the recovery stress rate (dσ/dT) is a constant no matter what the external constraint is. This is more or less out of the expectation, however, some experimental results have confirmed this[10]. Thus, the effect of the CTE value of the matrix on the dσ/dT value is completely negligible no matter how large the matrix CTE value is.
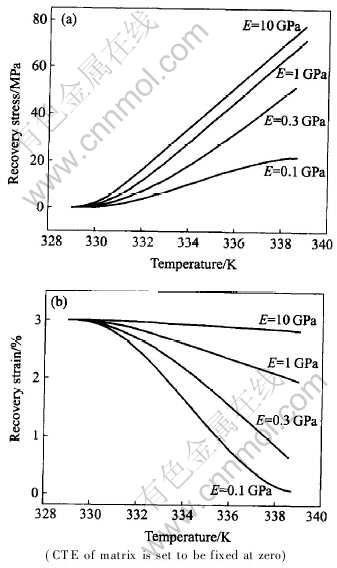
Fig.2 Effects of matrix modulus on recovery stress(a) and recovery strain(b) of embedded SMA wires
3.2 Effects of matrix modulus on actuation characteristics
Materials in reality have finite values of elastic modulus. SMA wires might be designed to reinforce different matrices with different stiffness. Fig.2 shows the calculated results under different matrix stiffness values. One can see from Fig.2(a) that for matrix materials with a very small modulus (i.e. 0.1GPa), the maximum recovery stress of the SMA is also limited within a small value (less than 20MPa as can be seen in Fig.2). Higher the matrix modulus is higher the maximum recovery stress is. For large matrix modulus, the recovery stress of the SMA wires keeps increase within a moderate temperature window. One interesting thing to note is that under different matrix modulus higher than 1GPa, the recovery stress rate (dσ/dT) of SMA elements has no significant difference, as can be seen in Fig.2(a). Typical modulus values of structural materials are within the scope from several decades of GPa to several hundreds of GPa, thus the stress rate (dσ/dT) of the embedded SMA wires should be the same. Our previous experiments have confirmed the conclusion that different constraining modulus has no significant effects on the recovery stress rate on SMA elements[15].
Fig.2(b) shows the recovery strain of SMA elements vs temperature under different constraining conditions. Similar with the results in Fig.1, one can see from Fig.2(b) that the strain is more sensitive to external constraining conditions than stress does. Even when the constraining modulus is large enough to make the recovery stress rate (dσ/dT) stabilized on a fixed value, the strain rate (dε/dT) is still changing significantly with different constraining modulus. Although there is no direct experimental evidence of Fig.2(b), the preliminary experimental results[6] did show that if some additional fibers were added into a SMA/epoxy composite, which would modify the stiffness of the matrix, and the composite showed quite different recovery strain behaviors upon heating. Further analysis of the experimental results of Ref.[6] is necessary before it can be used as an evidence of Fig.2(b), which is in progress.
3.3 Effects of matrix stress distribution on interface
One can learn from the above that both the CTE and modulus values of the matrix can define the maximum recovery stress of the embedded SMA elements. However, in reality, the interface of a composite in reality always debonds before the recovery stress of the embedded SMA elements reaches its maximum value. Our previous experiments showed that additional fibers such as glass fibers or Kevlar fibers present in the matrix might have a significant effect on the interface[6]. Results show that TiNiCu wires reinforced Kevlar fiber/epoxy composites have a better interface quality than that of a TiNiCu wires reinforced glass fiber/epoxy composites. Using the model built in section 2, the difference of normal stresses in the axial direction between the SMA elements and the epoxy matrix can be calculated. The results is shown in Fig.3, and one can see that the normal stress difference between the SMA and the epoxy matrix in SMA/Kevlar/epoxy composite is smaller than that in SMA/glass/epoxy composite.
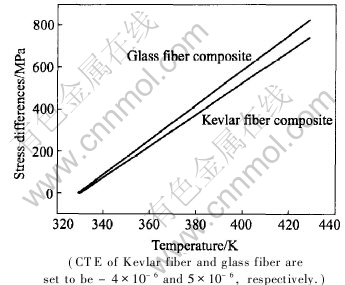
Fig.3 Effects of additional fibers on stress difference in axial direction between SMA and epoxy matrix
Results in Fig.3 can be regarded as the numerical proof of our previous experimental results[6]. Prestrained SMA wires embedded in a matrix contracts upon heating, and induces large internal thermal stresses at the interface. Additional reinforcing fibers with a negative expansion coefficient such as Kevlar fibers (typically -4×10-6/K) can partly relieve the mismatch stress between the TiNiCu wires and the matrix. Glass fibers have a thermal expansion coefficient of about 5×10-6/K, much less than that of the epoxy matrix (of about 60×10-6/K). Obviously, the added glass fiber will also impede the large thermal expansion of the epoxy matrix, and thus can partly relieve the mismatch stress between the TiNiCu wires and the matrix, but to a less extent than the Kevlar fibers do. Therefore, the TiNiCu wire-epoxy matrix interface of the Kevlar fiber composite can survive up to a higher temperature than the glass fiber composite. One can see from Fig.3 that the model built in section 2 qualitatively explains the above phenomenon.
4 CONCLUSIONS
1) The CTE value of the matrix has no effect on the recovery stress rate (dσ/dT) but has a significant effect on the recovery strain rate (dε/dT) of the SMA elements. A higher CTE value of the matrix defines a higher maximum recovery stress of the SMA elements.
2) Small matrix modulus has a significant effect on the recovery stress rate (dσ/dT), but the effect vanishes if the matrix modulus become sufficiently large. However, the matrix modulus has a significant effect on the recovery strain rate (dε/dT) of the SMA elements. A higher matrix modulus value defines a higher maximum recovery stress of the SMA elements.
3) Additional fibers have a significant effect on the quality of the interface between the SMA elements and the matrix. Calculations confirm that additional fibers with a smaller CTE value are more helpful in improving the interface quality than the fibers with a larger CTE value do.
REFERENCES
[1]Wei Z G, Sandstrm R, Miyazaki S. shape memory materials and hybrid composites for smart systems. Part II shape memory hybrid composites [J]. J Mater Sci, 1998, 33(15): 3763-3783.
[2]Zheng Y J, Cui L S, Schrooten J. Basic design guidelines for SMA/epoxy smart composites [J]. Mater Sci Eng A, 2005, A390: 139-143.
[3]Wei Z G, Sandstrm R, Miyazaki S. Shape memory materials and hybrid composites for smart systems. Part I shape memory materials [J]. J Mater Sci, 1998, 33(15): 3743-3762.
[4]Zheng Y J, Cui L S, Zhang F, et al. Effects of predeformation on the reverse martensitic transformation of TiNi shape memory alloy [J]. J Mater Sci Technol, 2000, 16(6): 611-614.
[5]Zheng Y J, Cui L S, Zhu D, et al. Constrained phase transformation of prestrained TiNi fibers embedded in metal matrix smart composite [J]. Mater Lett, 2000, 43(3): 91-96.
[6]Zheng Y J, Cui L S, Schrooten J. Effects of additional reinforcing fibers on the interface quality of SMA wire/epoxy composites [J]. J Mater Sci Forum, 2005, 475-479: 2047-2050.
[7]Xing T Y, Zheng Y J, Cui L S. Recovery stress characteristics of TiNi alloy wires after partial martensitic transformation under different constraint conditions [J]. Trans Nonferrous Met Soc China, 2005, 15(2): 336-339.
[8]Zheng Y J, Schrooten J, Tsoi K, et al. Thermal response of glass fibre/epoxy composites with embedded TiNiCu alloy wires [J]. Mater Sci Eng A, 2002, A335(1-2): 157-163.
[9]Zheng Y J, Schrooten J, Tsoi K, et al. Qualitative and qualitative evaluation of the interface in activated shape memory alloy composites [J]. Exp Mech, 2003, 43(2): 194-200.
[10]Vokoun D, Stalmans R. Recovery stresses generated by NiTi shape memory wires [A]. Proc SPIE Smart structures and Materials: Mathematics and Control in Smart structures [C]. California: Newport Beach, 1999, 3667: 825-835.
[11]Stalmans R, Van Humbeeck J, Delaey L. Modelling of the thermomechanical behaviour of shape memory wires embedded in matrix materials [A]. Proc 3rd International Conference on Intelligent Materials (ICIM/ECSSM96) [C]. Lyon: Bellingham, Wash, 1996, 2779: 511-516.
[12]Brinson L C, Huang M S. Simplifications and comparisons of shape memory alloy constitutive models [J]. J Intell Mater Syst Struct, 1996, 7(1): 108-118.
[13]ZHENG Yan-jun, CUI Li-shan, YANG Da-zhi. Kinetics model for martensitic transformation in shape memory alloys (SMAs) [J]. Acta Compos Sin, 2000, 17(1): 81-85. (in Chinese)
[14]Zheng Y J, Schrooten J, Cui L S. Thermomechanical properties of TiNiCu12 wire reinforced Kevlar/epoxy composites [J]. Intermetallics, 2005, 13(4-5): 1305-1309.
[15]Huai L M, Cui L S, Zhang L B, et al. Effects of bias springs on actuation and transformation behaviors of TiNi wires [J]. Mater Sci Forum, 2005, 475-479: 1929-1932.
(Edited by LONG Huai-zhong)
Foundation item: Project supported by the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry; Project(50471021) supported by the National Natural Science Foundation of China
Received date: 2005-01-14; Accepted date: 2005-09-28
Correspondence: CUI Li-shan, Professor; Tel: +86-10-89734055; E-mail: lshcui@cup.edu.cn


