
Compressive behavior and energy absorption of metal porous polymer composite with interpenetrating network structure
LIU Yu, GONG Xiao-lu
Institut Charles Delaunay, CNRS FRE 2848, LASMIS, UTT 12, rue Marie Curie, BP 2060, 10010 Troyes, France
Received 10 April 2006; accepted 25 April 2006
Abstract:
Interpenetrating phase composites (IPCs) are a new class of composite materials with improved combinations of mechanical and physical properties. This study was performed on a new type of IPC called metal porous polymer composite (MPPC) with an interpenetrating network structure. Aluminum-polypropylene (Al-PE) and Aluminum-epoxy resin (Al-Ep) composites were produced by infiltrating the polymer in the aluminum foam. The composite microstructures were characterized using SEM observation. The compressive behavior and energy absorption characteristics of MPPC were investigated and compared with the aluminum foams. The compressive modulus of composite was compared with the VOIGT–REUSS bounds and HASHIN-
Key words:
MPPC composite; microstructure; compressive behavior; energy; modulus;
1 Introduction
There is currently an interest in using porous aluminum or aluminum foams due to their potentials of relatively high yield strength, low density and energy absorption for the applications which require significant mass reductions and superior impact energy absorption[1]. However, one of the major disadvantages of metal foam is its low compressive strength[2-7]. We can believe that its cellular structure can be used for energy absorption during compressive or impact loading. In this case, the metal foam needs to be strengthened and its energy absorption capacity has to be improved without increasing its mass. To achieve this purpose, our idea is to introduce polymers into open cell metal foams, thus producing a new type of composite called metal porous polymer composite(MPPC)[8].
These new types of composites have interpenetrating microstructures in which both phases are interconnected three-dimensionally, forming a topologically continuous network throughout the structure. This kind of structure is completely different from the traditional fibre composites. Such interpenetrating microstructures offer improved combinations of mechanical and physical properties[9-11]. Some work has been done on the ceramic matrix composite reinforced with continuous metallic phase[12-14] and polymer composites[15-18]. However, little such work has been done in the case of metal-polymer composite yet.
In this paper, we describe the manufacture of two types of MPPC: Aluminium-polyethylene composite (Al-PE) and Aluminium-epoxy composite (Al-Ep) using the infiltration method. Their microstructures are observed by using the scanning electron microscopy (SEM). The mechanical behaviours of these two composites under compressive loading are characterized and compared with that of pure aluminium foams.
2 Experimental2.1 Specimen manufacture and preparation
In this study, all the MPPCs were manufactured using a vacuum assisted of low negative pressure molding process. This manufacture can be generalized as two stages: firstly, pure aluminum foams are produced by infiltration technology. In this process, high-power vacuum pump is used to shorten the time of pumping and produce the negative pressure for introducing the melting aluminum alloy into the pre-form. The aluminum alloy AS7G is chosen as the matrix alloy thanks to its good mechanical properties. Secondly, after the preparation of aluminum foams, two types of MPPC were realized by infiltrating the different polymer into the aluminum foams with various volume fractions. The aluminum foam is inserted into a similar mould and the polymer is placed on top of the foam. After the fusion of polymer, it infiltrates the aluminum foams with the negative pressure. When the infiltration is complete, the composite was cold at room temperature and cut to the specimen size.
2.2 Conditions of compression tests
Quasi-static compression tests were carried out at room temperature; the speed of travel in compression was imposed in 2 mm/min. The compressive specimens were 20 mm×20 mm×20 mm. The compressive direction is horizontal to the direction of these SEM photos. Effective elastic modulus was determined from the slope of the linear portion of the initial compression stress-strain curve.
3 Results and discussion3.1 Morphology and microstructure analysis
Fig.1 shows the SEM images of the polished surfaces of the MPPC. Fig.1(a) presents the Al-PE microstructure with approximately 63% PE where the white phase is Al and the gray phase is PE. The average thickness of skeleton “Al” is about 0.5 mm and its interspacing is about 1.2 mm. The pre-form of Al is thoroughly infiltrated and the interconnected network structure is evident. Fig.1(b) shows the typical interface Al-PE of the composite with higher magnification. Especially, due to the cooling rate and the large mismatch of the CTE (coefficient of thermal expansion) between the Al matrix and the PE reinforcement, we can observe some cracks in the Al-PE interface. Fig.1(c) shows the microstructure of Al-Ep which has the same form as the composite Al-PE because of using the same Al foam. However, there is no crack observed in the interface between Al and Ep. This is because the epoxy resin was infiltrated in the pre-form Al at room temperature, the influence of CTE is relatively small, and thus the residual stresses between Al and Ep are low.
3.2 Compressive behavior
After having manufactured the MPPC specimens, we performed mechanical tests in order to understand their compressive behaviour.
Fig.2 shows the comparison of compressive stress-stain curves of solid Al, Al-Ep, Al-PE and Al foam with the same porosity of 63%. We can see that the solid Al specimens show a typical compressive behavior of
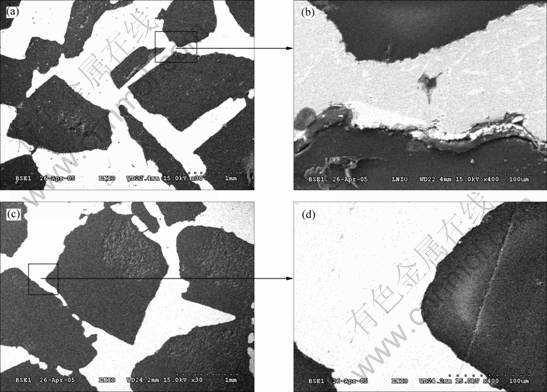
Fig.1 SEM images of composite samples: (a) Structure of composite Al-PE; (b) Interface between Al and PE; (c) Structure of composite Al-Ep; (d) Interface between Al and Ep
dense metal. The stress increases linearly within the elastic regime followed by a fully-plastic regime. In comparison, the stress strain results of Al foam can be interpreted by the GIBSON-ASHBY theory, in which the compressive stress-strain process of foam was divided into 3 stages: elastic, plateau and densification stage. However, these stresses of two composites (Al-Ep and Al-PE) elevate sharply with compressive strain followed by a sustained plateau region where the yielding happens due to the interfacial cleavage or skeleton of foam being destroyed. In fact, the process of deformation strongly depends on many material factors, for example, the density of foam, the infiltrated polymer etc. In general, the stress-strain curves of two composites are of similar form between those of Al and foam, but the ranges of values are different.
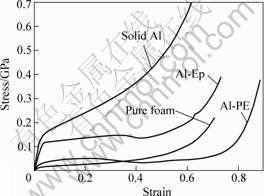
Fig.2 Comparison of compressive behavior for Al, two composites and Al foam with the same proportion of polymer (63%)
The compressive modulus of two composites (Al-PE, Al-Ep) and the pure Al foam, denoted as EEPC, EPEC,, and EFC respectively, as function of proportion of polymer are shown in Fig.3. It can be seen that the compressive modulus decreases almost linearly with the increase of the proportion of polymer from 54% to 68%. The moduli of composites and foam are in an order
EEPC>EPEC>EFC. From Fig.3 we can see that EEPC is higher almost 1.5-2 times than EFC at different proportions of polymer. It shows that the compressive modulus of foam is improved by the polymer introduction in the pure foams. Moreover, the amplitude of variation of modulus is determined by the type of introduced polymers.
The energy absorbed (W) by unit volume due to a strain ε is simply the area under the stress–strain curve and can be written as
![]() (1)
(1)
where σ(ε) is the stress as a function of the strain.
It is obvious that the more the stress plateau of the
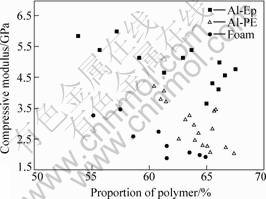
Fig.3 Compressive modulus for composites and pure foam as function of polymer proportion
stress-strain curve is important, the more the capacity for absorption of energy is important. As can be seen from Fig.2, among the four materials, the pure aluminum foam has the lowest stress–strain curve thus it has the weakest absorption compared with composite.
Fig.4 shows that the comparisons of energy absorption of Al-Ep, Al-PE and Al foam. It indicates that compared with the aluminum foam, the energy absorbed by the Al-Ep is more than 50 MJ/m3 at the strain of 40% while that absorbed by the aluminum foam is only around 10 MJ/m3 according to Eqn.(1).
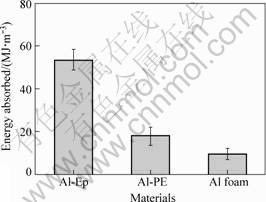
Fig.4 Comparison of energy absorption of Al-Ep, Al-PE and Al foam with same proportion of Al 0.3 at strain of 40%
It is therefore suggested that the energy absorption behavior of metallic foams could be favorably modified by polymer introduction in the cells. Particularly, the improvement in absorption efficiency should make the impact protection more effective and more reliable. However, the absorbed energy strongly depends on the proportion of polymer, interfacial strength etc.
3.3 Theoretical models
While studying the characteristics of composites reinforced by polymer MPPC, it is necessary to propose or use a theoretical model to describe the relation between its properties and microstructure, which can further help to design microcellular composite with controllable mechanical properties.
Currently, many theoretical models have been developed to describe and predict the elastic properties of two-phase materials. VOIGT proposed the first model under a uniform strain assumption[19]. The elastic modulus, E of the two-phase material can be estimated as
![]() (2)
(2)
with Va+Vb=1, where Va and Vb are the volume fraction of the two phases. Under a uniform stress assumption as proposed by REUSS, the elastic modulus of the two-phase material can be expressed by
![]() (3)
(3)
where the superscript “u” and “l” presents upper and lower bound, respectively. The values predicted by Eqns. (2) and (3) are frequently treated as the upper bound and lower bound of the elastic modulus of two-phase material, respectively. The VOIGT–REUSS bounds are thus also used in the present study to compare the experimental data, as shown in Fig.5. However, it is not accurate adequately and the modifications have a ccordingly been proposed by many researchers.
More restrictive bounds on the effective properties

Fig.5 Comparison of compressive modulus of composites with VOIGT-REUSS bound and H-S bound model as function of polymer content: (a) Al-Ep; (b) Al-PE
of isotropic two dimensional composites were found by HASHIN using the HASHIN and SHTRIKMAN variation method[20]. The bounds can be presented as the two-sided inequalities:
![]() ≤
≤![]() ≤
≤![]() ,
, ![]() ≤
≤![]() ≤
≤![]() (4)
(4)
where K and G are the bulk modulus and shear modulus, respectively.
Fig.5 shows all the experimental data on the compressive modulus of the composite Al-Ep and Al-PE as function of polymer content, and the VOIGT-REUSS bound and H-S bound are also shown in Fig.5 for this comparison. All the available experimental data of compressive modulus for the composite cover only a small composition range, from 54% to 64%. This is the result of the limit porosity of metallic foam with this manufacturing method. The VOIGT-REUSS bounds are close to each other as the elastic module of the two phases, such as the cases of metal matrix composites. However, for our composites MPPC with two phases of strongly different elastic modulus, such as Al-PE composites, the upper and lower bounds are widely apart. In any case, all the experimental data are well limited within the VOIGT-REUSS bounds.
It can see from Fig.5, most experimental data also fall within the H-S bounds. Since the H-S bounds are relatively closer to each other than those of the VOIGT-REUSS bounds, the H-S model offers closer bounds on the estimation of compressive modulus for composites. Therefore, the VOIGT-REUSS and H-S bounds can be applied to estimate the elastic modulus of the composites with interpenetrating microstructure. In our case, these models on compressive modulus show little dependence on microstructure features. However, there are also some deviation between experimental data and theoretical predictions. This is frequently attributed to the micro-structural complexity of real composites and the interactions between each phase of composite. Therefore, more models should be proposed which account for the interconnectivity and interface characteristics.
4 Conclusions
A new type of metal porous polymer composite(MPPC) with an interpenetrating network structure is analyzed which has great potential for future development owing to its special reinforcement structure. The influence of reinforced material and structure of cells is more significant than that of interfacial effect on the mechanic behavior of compression. The compressive behaviors of these two composites were investigated and compared with those of the aluminum foam and the bulk polymer. The composites show improved compressive behavior and enhanced energy absorption capacity compared with the pure aluminum foam. The experimental data of compressive modulus are compared with the VOIGT-REUSS and HASHIN-SHTRIKMAN (H-S) bounds models. The model predictions offer upper and lower bounds to compensate the scatter of the data. The compressive modulus of the composites falls well within the VOIGT-REUSS bounds and H-S bounds.
References
[1] GIBSON L J, ASHBY M F. Cellular Solids: Structure and Properties[M]. 2nd ed. Cambridge: Cambridge University Press, 1997.
[2] DUBBELDAY P S. Poisson’s ratio of foamed aluminum determined by laser doppler vibrometry[J]. J Acoust Soc Am, 1992, 91: 1737-1744.
[3] DUBBELDAY P S, RITTENMYER K M. Shear modulus determination of foamed aluminum and elastomers[J]. New York: Ultrasonics Symposium, IEEE, 1985. 1052-1055.
[4] WEBER M, BAUMEISTER J, BANHART J, KUNZE H D. Selected mechanical and physical properties of metal foams[A]. Proceedings of the Powder Metallurgy World Congress PM94[C]. Paris, 1994. 585-588.
[5] PRAKASH O, SANG H, EMBURY J D. Structure and properties of Al-SiC foam[J]. Mater Sci Eng, 1995, A199: 195-203.
[6] BEALS J T, THOMPSON M S. Density gradient effects on aluminum foam compression behaviour[J]. J Mater Sci, 1997, 32: 3595-3600.
[7] SUGIMURA Y, MEYER J, HE M Y, BART-SMITH H, GRENESTEDT J, EVANS A G. On the mechanical performance of closed cell foams[J]. Acta Mater, 1997, 45: 5245-5259.
[8] GONG X L, LIU Y, HE S Y, LU J. Manufacturing and low-velocity impact response of a new composite material: metal porous polymer composite(MPPC)[J]. Journal of Materials Science and Technology, 2004, 20(Suppl.1): 65-68.
[9] WEGNER L D, GIBSON L J. The mechanical behaviour of interpenetrating phase composites—I: modeling[J]. International Journal of Mechanical Sciences, 2000, 42(5): 925-942.
[10] WEGNER L D, GIBSON L J. The mechanical behaviour of interpenetrating phase composites—II: a case study of a three-dimensionally printed material[J]. International Journal of Mechanical Sciences, 2000, 42(5): 943-964.
[11] BRESLIN M C, RINGNALDA J, XU L, FULLER M, SEEGER J, DAEHN G S, OTANI T, FRASER H L. Processing, microstructure, and properties of co-continuous alumina-aluminum composites[J]. Mater Sci Eng, 1995, A195: 113-119.
[12] DAEHN G S,STARCK B, XU L,ELFISHAWY K F,RINGNALDA J,FRASER H L. Elastic and plastic behavior of a co-continuous alumina/aluminum composite[J]. Acta Mater, 1996, 44: 249-261.
[13] DE SOUZA RM, YOSHIMURA H N, XAVIER C, GOLDENSTEIN H. Strengthening porous ceramics by molten metal infiltration[J]. Key Eng Mater, 1997, 127-131: 439-446.
[14] SKIRL S,HOFFMAN M, BOWMAN K, WIEDERHORN S,RODEL J. Thermal expansion behavior and macrostrain of Al2O3/Al composites with interpenetrating networks[J]. Acta Mater, 1998, 46: 2493-2499.
[15] CHIANG W Y, CHANG D M. Synthesis and properties of simultaneous interpenetrating networks based on poly (urethane-epoxy)/allyl novolac resin[J]. J Mater Sci, 1997, 132: 4985-4990.
[16] KARABANOVA L, PISSIS P, KANAPITSAS A, LUTSYK E. Thermodynamic state, temperature transitions, and broadband dielectric relaxation behavior in gradient interpenetrating polymer networks[J]. J Appl Polym Sci, 1998, 68: 161-171.
[17] ZHANG Y, HOURSTON D J. Rigid interpenetrating polymer network foams prepared from rosin-based polyurethane and an epoxy resin[J]. J Appl Polym Sci, 1998, 69: 271-281.
[18] ASHBY M F. Criteria for selecting the components of composite[J]. Acta Metall Mater, 1993, 41: 1313-1335.
[19] VOIGT W. On the relation between the elasticity constants of isotropic bodies [J]. Ann Phys Chem, 1989, 274: 573-587.
[20] HASHIN Z, SHTRIKMAN S. A variational approach to the theory of the elastic behavior of multiphase materials[J]. J Mech Phys Solids, 1963, 11: 127-140.
Foundation item: Project supported by Conseil Général de l’Aube (district grant) and the European Social Fund
Corresponding author: LIU Yu; E-mail: yu.liu@utt.fr


