
Effect of vacancy defects on electronic properties and activation of sphalerite (110) surface by first-principles
CHEN Jian-hua(陈建华)1, CHEN Ye(陈 晔)2, LI Yu-qiong(李玉琼)2
1. College of Resources and Metallurgy, Guangxi University, Nanning 530004, China;
2. College of Chemistry and Chemical Engineering, Guangxi University, Nanning 530004, China
Received 2 June 2009; accepted 25 August 2009
Abstract:
The electronic properties of sphalerite (110) surface with Zn-vacancy and S-vacancy were calculated by using density-functional theory, and the effects of vacancy defect on the copper activation of sphalerite were investigated. The calculated results indicate that surface state occurs in the band gap of Zn-vacancy sphalerite, which is from the contribution of S 3p orbital at the first layer of the surface. The presence of S-vacancy results in surface state appearing near the Fermi level and the bottom of conductor band, which are composed of S 3p and Zn 4s orbital, respectively. The surface structure of Zn-vacancy sphalerite is more stable than S-vacancy surface due to the occupation of Zn-vacancy by Cu atoms; hence, the substitution reaction of Cu for Zn vacancy is easier than the substitution of Cu for Zn atoms with S-vacancy surface.
Key words:
sphalerite; vacancy defect; Density Functional Theory calculations; copper activation;
1 Introduction
In the flotation of nonferrous metal sulfide ore, the types and contents of impurities play an important role, which can affect the electrochemical properties and flotation behaviors of sulfide minerals[1-2]. Perfect sphalerite has a wide band gap (3.6 eV) and can be taken as an insulator[3]. The presence of defects in the sphalerite crystal can greatly enhance the conductivity[4]. The defects of sphalerite crystal can be classified into two types: one is the deviation of stoichiometry, which is generally shown as the deviation of 1?1 for the value of Zn-to-S molar ration (Zn/S), and the other is the presence of impurities in the sphalerite crystal. The effects of impurity defect on the sphalerite properties mainly depend upon the type of heteroatom. In practice, the heteroatom types and contents in sphalerite crystal are varied with the different deposits, for example, we called the sphalerite containing iron impurity as marmatite, and the sphalerite bearing cadmium impurity as pshibramite[5]. However, the vacancies exist commonly in the sphalerite crystal. The deviation of stoichiometry will occur in the process of crystallization of sphalerite due to the variation of temperature and pressure. Sulfur vacancy and zinc vacancy exist in sphalerite crystal in practice.
Studies of electrochemistry of sulfide ore flotation show that the anodic oxidation of xanthate occurs on the mineral surface with a corresponding catholic reduction of oxygen at the same time[6]. Oxygen could not be adsorbed on the perfect sphalerite surface due to its wide band gap; as a result, anodic oxidation of xanthate fails to occur. The band gap of sphalerite is reduced and the conductivity is enhanced when the sphalerite crystal contains impurities, which is advantageous to the adsorption of oxygen on the surface of sphalerite. The defects of crystal can be classified into donor defect and acceptor defect. Anionic defect is a donor one (Zn/S>1) which increases the concentration of electrons; and cationic defect is an acceptor one (Zn/S<1) which increases the concentration of holes. In addition, the vacancy will influence greatly the geometry structure of the surrounding atoms, and the great relaxation of surface will occur, which results in the alteration of the electronic properties of sphalerite. Therefore, the investigation of the influence of vacancy defects on the electronic properties of sphalerite surface is helpful to further understanding the nature of the role of crystal defects in the sphalerite flotation.
In this work, the first-principles quantum mechanics calculation was performed to examine the effects of S-vacancy and Zn-vacancy on the electronic properties of sphalerite (110) surface, then the effects of vacancies on copper activation on sphalerite were studied.
2 Computational method and model
Calculations have been done using Cambridge serial total energy package (CASTEP) developed by PAYNE et al[7], which is a first-principle pseudopotential method based on the density-functional theory (DFT). DFT calculations employing plane wave (PW) basis sets and ultrasoft pseudopotentials have been used[8-9]. The exchange correlation functional used was the generalized gradient approximation (GGA) developed by PERDEW, BURKE and ERNZERHOF (PBE)[10]. The interactions between valence electrons and ionic core were represented by ultra-soft pseudopotentials. Valence electron configuration considered in this study included Zn 3d104s2, S 3s23p4 states. The kinetic energy cutoff (310 eV) of the plane wave basis was used throughout, and the Brillouin zone was sampled with special k-points of a 4×5×1 grid for all structure calculations[11], which shows that the cutoff energy and the k-points mesh were sufficient for the system. For self-consistent electronic minimization, the Pulay Density Mixing method was employed with the convergence tolerance of 2.0×10-6 eV/atom. The energy tolerance was 2.0×10-5 eV/atom; the force tolerance was 0.05 eV/?; and the displacement tolerance was 0.002 ?.
Zinc sulfide is naturally observed in two polymorphs, zinc blende and wurtzite, with cubic and hexagonal lattice structures, respectively[12]. The calculation is based on zinc blende structure in which space group is F-43M. The cell parameter is a=b=c=0.540 93 nm and α=β=γ=90?. The surface structures of zinc blende sphalerite have been well documented. Studies using X-ray photoelectron spectroscopy (XPS), low energy electron diffraction (LEED), and theoretical methods have shown that the ZnS (110) surface undergoes considerable relaxation, resulting in a low surface free energy[13]. However, different crystal planes in the sphalerite structure such as (111), (111) and (001) undergo significant reconstruction to lower their surface free energies[14]. Calculations carried out by WRIGHT et al[15] indicate that these reconstructed surfaces are still of higher energy than that of (110). Therefore, the sphalerite (110) cleavage plane was chosen for the calculation in this study.
The construction of sphalerite (110) plane was as follows. The first step is to optimize primitive cell. The equilibrium lattice parameters of ZnS of 0.545 51 nm is close to the experimental value of 0.540 93 nm. The second step is to cleave a 5 atomic-layer slab of sphalerite (110) plane based on the optimized primitive cell, creating a 2×2×1 super-cell shown in Fig.1. The thickness of vacuum slab was 15 ?. Finally, the geometric optimization of sphalerite (110) plane was performed.
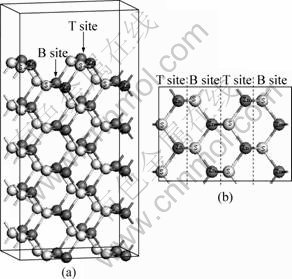
Fig.1 Model of sphalerite (110) surface: (a) Side view; (b) Top view
It can be seen from Fig.1 that there are two possible sites to form vacancy for Zn or S atom in each layer: top (T) site and bottom (B) site. In order to find the most stable vacancy site, the geometry optimization calculations of possible sites for Zn or S atom in top three layers have been performed. The vacancy formation energy of sphalerite (110) surface is defined as
![]() (1)
(1)
where ![]() and
and ![]() are the total energies of the slab with and without a vacancy, respectively. μX represents the atomic chemical potential of Zn or S atom. Here, we define the atomic chemical potential as a calculated total energy per atom in its optimized reference state[16-17]. More negativity of ΔEfor indicates that the vacancy is easier to form.
are the total energies of the slab with and without a vacancy, respectively. μX represents the atomic chemical potential of Zn or S atom. Here, we define the atomic chemical potential as a calculated total energy per atom in its optimized reference state[16-17]. More negativity of ΔEfor indicates that the vacancy is easier to form.
3 Results and discussion
3.1 Geometry optimization of vacancy
The five-layer slab has been used to model sphalerite (110) surface. The structure of sphalerite (110) surface unit cell is shown in Fig.2, and the values of structural parameters are listed in Table 1. The data in Table 1 show that the theoretical optimization structure of perfect sphalerite (110) surface agrees with the experimental results by VAUGHAN et al[13],which indicates that the computer method and parameters used in calculation are sufficient to model sphalerite (110) surface.
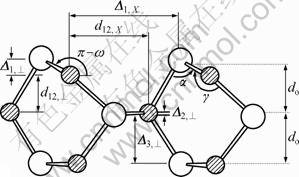
Fig.2 Side view of ZnS (110) surface unit cell
Table 1 Structural parameters for perfect ZnS (110) surface relaxation

It can be seen from Fig.1 that there are two possible sites for Zn or S atom to form vacancy per layer. In this study, top three layers are considered to model the outer surface. The optimizations of sphalerite (110) surface with Zn or S atom vacancy at all possible sites for top three layers have been performed. The vacancy formation energy values are listed in Table 2. It can be seen from Table 2 that both Zn vacancy and S vacancy cannot be formed spontaneously in ordinary condition due to greater positive formation energy. As a matter of fact, Zn or S vacancy is easy to form in the process of crystallization of sphalerite at high metallogenic temperature. The lowest formation energies of Zn vacancy and S vacancy on T site of the 1st layer indicate that T site is the most stable structure for Zn and S vacancy on the sphalerite (110) surface.
Table 2 Vacancy formation energy values at different sites on sphalerite (110) surface (kJ/mol)
The structure parameters for the ZnS (110) surface relaxation with vacancies are listed in Table 3. It can be seen from Table 3 that the presence of vacancies results in large relaxation of sphalerite (110) surface compared with Table 1. For Zn vacancy, all structure parameters of sphalerite (110) surface are changed except for Δ2,⊥. Among them, the value of Δ1,⊥ decreases by 23.6%, and d12,⊥ increases by 28.9% compared with perfect sphalerite surface. For S-vacancy, the relaxation of sphalerite (110) surface is very different with Zn-vacancy. Only the value of d12,⊥ increases by 33.56% compared with perfect sphalerite, and others are near to perfect sphalerite. Therefore, Zn-vacancy has a greater influence on the geometry structure of sphalerite (110) surface than S-vacancy.
Table 3 Structural parameters for ZnS (110) surface relaxation with vacancies

3.2 Effects of vacancies on band structure
Fig.3 shows the band structure of perfect, Zn- vacancy and S-vacancy sphalerite (110) surface. Compared with the perfect sphalerite, surface states can be obviously observed in the band gap for Zn-vacancy and S-vacancy sphalerite. Fig.3 indicates that surface state appears near the Fermi level for sphalerite surface with Zn-vacancy defect, and further analysis shows that this surface state is from the contribution of S 3p orbital at the first layer of sphalerite surface. For S vacancy, the surface states are more complex, and surface state can be observed below conduction band and above valence band. Further analysis shows that these surface states are from the contribution of S 3s, 3p orbital and Zn 4s orbital at first layer of sphalerite surface.
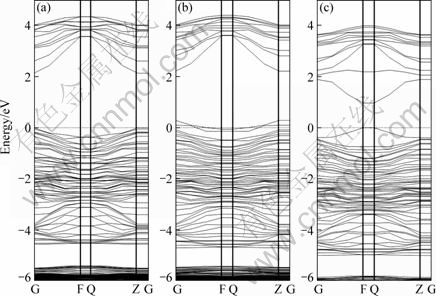
Fig.3 Band structures of perfect (a), Zn-vacancy (b) and S-vacancy (c) sphalerite (110) surface
In addition, Fig.3 also indicates that perfect sphalerite (110) surface is p-type, and the Fermi level positions in the band gap for Zn-vacancy and S-vacancy sphalerite surfaces are changed. The presence of S-vacancy increases the Zn atom concentration, which results in an increase of electron concentration of sphalerite, hence the conductivity of S-vacancy sphalerite increases, especially in the F-Q direction.
3.3 Effect of vacancies on density of states
The density of states (DOS) of electrons in top three layers for perfect, Zn-vacancy and S-vacancy sphalerite (110) surface are shown in Figs.4(a), (b) and (c), respectively. Fig.4(a) indicates that there is not any surface state at the first layer for perfect sphalerite surface; in addition, distributions of DOS for top three layers are almost the same, which indicates that surface DOS of sphalerite is the same as that of the bulk. This can be explained from the fact of little surface relaxation of sphalerite.

Fig.4 DOS maps of top three layers of perfect (a), Zn-vacancy (b) and S-vacancy (c) sphalerite (110) surface
For Zn-vacancy, it can be seen from Fig.4(b) that surface state can be observed at Fermi level for the first layer, which is composed of S 3p orbital. Fig.4(c) manifests that the presence of S-vacancy results in surface state appearing near the Fermi level and the bottom of conductor band, which are composed of S 3p and Zn 4s orbital, respectively.
In addition, Fig.4 manifests that S or Zn vacancy at the first layer of sphalerite (110) surface can only influence the DOS of the first layer; and the DOS of the second layer and the third layer keep unchanged.
3.4 Effects of vacancies on Cu activation
The copper activation plays an important role in the flotation of sphalerite. It is necessary to add copper to activate sphalerite before the flotation of sphalerite. The mechanism of copper activation of sphalerite indicates that the Zn atom on the sphalerite will be replaced by copper atom[18]. For Zn or S vacancy, the surface structure and state are different from the perfect sphalerite surface; hence it is necessary to investigate whether the vacancy defect would affect the substitution of Cu for Zn on the sphalerite surface.
The reaction of Cu with sphalerite can be written as
Zn40S40+Cu→CuZn39S40+Zn (2)
The possible sites of Zn atom substituted by Cu atom have been calculated by DFT. The results indicate that the top site atom at the first layer of sphalerite (110) surface is the most stable site for Cu substituting for Zn atom, and the substitution energy is -110.96 kJ/mol. For sphalerite surface bearing vacancy, the reaction of Cu with sphalerite can be written as
For S vacancy:
Zn40S39+Cu→CuZn39S39+Zn (3)
For Zn vacancy:
Zn39S40+Cu→CuZn39S40 (4)
For Zn vacancy, the substitution energy of Cu for Zn vacancy is -594.22 kJ/mol, which is more negative than that of perfect sphalerite (-110.96 kJ/mol). This can be explained that the structure of sphalerite (110) surface is more stable when the Zn vacancy is replaced by Cu atom. For S vacancy, the effect of Cu activation is more complex due to the still presence of S vacancy after substitution. Calculated results indicate that the substitution energy of the top Zn atom at first layer by Cu atom is -168.14 kJ/mol, which is greater than that of perfect sphalerite (-110.96 kJ/mol), but less than that of Zn-vacancy sphalerite (-594.22 kJ/mol). The possible reason is that the restriction of Zn atom is less than the perfect sphalerite due to the lack of S atoms for S- vacancy sphalerite, hence Zn atoms with S vacancy are easy to be replaced by Cu atoms. However, the surface structure of Zn-vacancy sphalerite is more stable than S-vacancy surface due to the occupation of Zn-vacancy by Cu atoms; hence, the substitution reaction of Cu for Zn vacancy is easier than the substitution of Cu for Zn atoms with S vacancy.
4 Conclusions
1) Surface state occurs in the band gap of Zn-vacancy sphalerite, which is from the contribution of S 3p orbital at the first layer of sphalerite (110) surface. The presence of S vacancy results in surface state appearing near the Fermi level and the bottom of conductor band, which are composed of S 3p and Zn 4s orbital, respectively, and the conductivity of S-vacancy sphalerite increases.
2) The structure of sphalerite (110) surface is more stable when the Zn vacancy is occupied by Cu atoms. For S vacancy, the substitution energy of top-site Zn atoms at the first layer by Cu atoms is -168.14 kJ/mol, which is greater than that of perfect sphalerite (-110.96 kJ/mol), but less than that of Zn-vacancy sphalerite (-594.22 kJ/mol). The surface structure of Zn-vacancy sphalerite is more stable than S-vacancy surface due to the occupation of Zn vacancy by Cu atoms; hence, the substitution reaction of Cu for Zn vacancy is easier than the substitution of Cu for Zn atoms with S vacancy.
References
[1] ZHANG Mao-jun, HU Wei-bo. Handbook of mineral processing [M]. Beijing: Metallurgy Technology Press, 1993: 22-24. (in Chinese)
[2] FENG Qi-ming, CHEN Jin. Electrochemistry of flotation of sulphide minerals [M]. Changsha: Central South University of Technology Press, 1993: 69-72. (in Chinese)
[3] HARMER S L, GONCHAROVA L V, KOLAROVA R, LENNARD W N. Surface structure of sphalerite studied by medium energy ion scattering and XPS [J]. Surface Science, 2007, 601: 352-361.
[4] XIONG Xiao-yong. Effect of the iron content of zinc sulphide concentrates on their semi-conductivity and chemical reactivity [J]. Nonferrous Metals, 1989, 41(4): 55-66. (in Chinese)
[5] TONG Xiong, SONG Shao-xian, HE Jian. Activation of high-iron marmatite in froth flotation by ammoniacal copper(Ⅱ) solution [J]. Mineral Engineering, 2007, 20(9): 259-263.
[6] CHEN Jian-hua, FENG Qi-ming, LU Yi-ping. Energy band model of electrochemical flotation and its application(Ⅰ)—Theory and model of energy band of semiconductor-solution interface [J]. The Chinese Journal of Nonferrous Metals, 2000, 10(2): 240-242. (in Chinese)
[7] PAYNE M C, TETER M P, ALLAN D C, ARIAS T A, JOANNOPOULOS J D. Iterative minimization techniques for ab initio total energy calculation: Molecular dynamics and conjugate gradients [J]. Reviews of Modern Physics, 1992, 64: 1045-1097.
[8] PERDEW J P, WANG Y. Accurate and simple analytic representation of the electron-gas correlation energy [J]. Physical Review B, 1992, 45: 13244-13249.
[9] VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism [J]. Physical Review B, 1990, 41: 7892-7895.
[10] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letter, 1996, 77(18): 3865-3868.
[11] MONKHORST H J, PACK J D. Special points for Brillouin-zone integrations [J]. Physical Review B, 1976, 13: 5188-5192.
[12] von OERTZEN G U, JONES R T, GERSON A R. Electronic and optical properties of Fe, Zn and Pb sulfides [J]. Journal of Electron Spectroscope, 2005, 144/147(6): 1245-1247.
[13] VAUGHAN D J, BECKER U, WRIGHT K. Sulphide mineral surfaces: Theory and experiment [J]. International Journal of Mineral Processing, 1997, 51: 1-14.
[14] HARMER S L, MIERCZYNSKA V A, BEATTIE D A. The effect of bulk iron concentration and heterogeneities on the copper activation of sphalerite [J]. Mineral Engineering, 2008, 21(11): 1005-1012.
[15] WRIGHT K, WATSON G W, PARKER S C, VAUGHAN D J. Simulation of the structure and stability of sphalerite (ZnS) surfaces [J]. American Mineralogist, 1998, 83: 141-146.
[16] KAZUME N, MASAHITO Y, MASAYUKI H. Energetic of Mg and B adsorption on polar zinc oxide surfaces from first principles [J]. Physical Review B, 2008, 77: 35330-35336.
[17] REUTER K, SCHEFFLER M. Composition, structure, and stability of RuO2 (110) as a function of oxygen pressure [J]. Physical Review B, 2001, 65: 035406.
[18] CHANDRA A P, GERSON A R. A review of the fundamental studies of the copper activation mechanisms for selective flotation of the sulfide minerals, sphalerite and pyrite [J]. Advances in Colloid Interface Science, 2009, 145(1): 97-110.
Foundation item: Project(50864001) supported by the National Natural Science Foundation of China
Corresponding author: CHEN Ye; Tel/Fax: +86-771-3233566; E-mail: fby18@126.com
DOI: 10.1016/S1003-6326(09)60169-2


