DOI: 10.11817/j.issn.1672-7207.2016.01.040
基于CCD的粉尘质量浓度光散射测量系统
张宸瑜1,李舒2,许传龙1,王式民1
(1. 能源热转换及其过程测控教育部重点实验室,东南大学 能源与环境学院,江苏 南京,210096;
2. 南京市计量监督检测院科技发展部,江苏 南京,210037)
摘 要:
测量粉尘颗粒质量浓度时,测量系统并不能满足角度积分上限为π和角度下限为0的固有缺陷,基于Mie理论数值计算散射光强的角分布,进而对质量浓度测量误差进行分析。利用电荷耦合元件(charge-coupled device, CCD)的高灵敏度、低噪声、线性度好等优点,研究并搭建一种基于CCD的光散射颗粒质量浓度测量系统,并通过已知孔径的小孔对CCD测量系统的角度分辨率和放大率进行校正,测试CCD的灵敏度及线性度。最后,利用已知粒径和质量浓度的样品对测量系统的准确性进行试验研究。研究结果表明:当散射角积分为0.03°~5°时,可满足质量浓度测量需要,测量相对误差小于15%。
关键词:
中图分类号:TN247 文献标志码:A 文章编号:1672-7207(2016)01-0290-08
A CCD–based measurement system for dust mass concentration through light scattering
ZHANG Chenyu1, LI Shu2, XU Chuanlong1, WANG Shimin1
(1. Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education,
School of Energy and Environment, Southeast University, Nanjing 210096, China;
2. Department of Science and Technology Development, Nanjing Institute of Measurement and Testing Technology,
Nanjing 210037, China)
Abstract: The scattering integration method can be applied to measure dust mass concentration. However, the measurement system based on scattering integration method has inherent disadvantages that the upper limit of the scattering angle is less than π and the lower limit is more than zero. The measurement error of dust mass concentration was analyzed through calculating angular distribution of scattering intensity. Considering that charge-coupled device (CCD) has advantages of high sensitivity, low noise and good linearity, a CCD-based measurement system for dust mass concentration was built. The angular resolution and magnification of the measurement system were calibrated through known-size pinholes, and the sensitivity and linearity of the CCD were tested. Finally, the experiments were carried out to evaluate the measurement system through the use of the polystyrene solutions with known particle sizes and concentrations. The results show that the influence of dust particle size on dust mass concentration measurement can be ignored and the scattering angle range within 0.03°-5° is enough for the dust mass concentration measurement using the scattering integration method. The measurement relative error of dust mass concentration is less than 15%.
Key words: dust mass concentration; CCD; scattering integration method; light scattering
随着工业的飞速发展,粉尘的危害也越来越严重。大气中的可吸入性粉尘会对人体的健康造成威胁[1],且一些可燃性粉尘存在爆炸性危险。实现粉尘质量浓度的在线监测,可以对环境污染进行有效监控,防止粉尘爆炸,燃煤电站煤粉质量浓度在线测量可以指导锅炉的优化调节等,因此,实现粉尘质量浓度在线测量具有重要意义。根据工作原理不同,粉尘质量浓度的测量方法可分为取样法和非取样法[2],其中,非取样法包括黑度法、光学法[3]、超声波衰减法[4]和电荷 法[5]等。随着激光技术的不断发展,光学法具有非接触测量、粒径测量范围宽、测量对象广、自动化程度高及预知参数少等优点,因而发展最为迅速。国外在20世纪70年代推出了基于消光理论[6]的烟尘浓度测量的浊度计,但相关研究发现消光法的吸收系数在实际的烟尘测量中不能作为常数,这对消光法的应用带来了很大限制。德国 Karl Sruhe研究中心研制的MESA (mass concentration extinction size analyzer)测量系统结合了消光法和压电振动法,可在线测量粉尘质量浓度及平均粒径,但测量装置复杂[7]。近些年,国内在利用散射光测量粉尘质量浓度方面进行了不少研究,主要是基于Mie散射理论[8]计算某一空间立体角的光通量,利用光通量与颗粒质量浓度呈正比关系的原理进行测量,也称为光度计法[9],但针对不同折射率及粒径分布下的颗粒群,光通量与颗粒质量浓度的关系曲线并不一致,故需重新标定。针对高质量浓度烟尘环境的测量,后向散射法[10]具有很大优势,但其在颗粒质量浓度较小时并不适用。散射积分法主要是利用颗粒的全部散射光强积分值测量颗粒质量浓度[11]。此方法基于Fraunhofer衍射理论,算法简单且计算速度快,适用于低颗粒质量浓度测量,其最大的优点是无需预知粒径分布便可直接获得粉尘质量浓度。因前向小角内的散射光强积分值近似等效于全部散射光强积分值,本文中粉尘质量浓度测量主要利用前向小角范围内散射光,采用散射积分法对颗粒质量浓度进行求解。散射积分法的假设条件中忽略了折射率及平均粒径对质量浓度测量结果的影响,在理论推导中也引用了近似等效条件,这都降低了测量系统的精确性。基于电感耦合元件(charge-couple device, CCD)的光散射粉尘质量浓度测量系统因透射光强远大于散射光强,测量时会采用针头反射镜反射透射光[12],带有小孔的反射镜反射散射光[13],遮挡CCD部分像素点等方法,避免中心透射光进入CCD,这些措施也必然导致0°附近极小范围内的散射光无法接收。此外,受CCD感光元件面积、光路孔径光阑等限制,最大散射光接收角也无法达到π,一般到10°左右。因此,测量系统无法满足散射积分法积分角下限为0、上限为π的理想条件,导致质量浓度测量误差。本文作者针对测量系统不能满足散射积分法的角度上限为π和下限为0的条件,对引起的质量浓度测量误差进行模拟,分析折射率、平均粒径和积分上下限引起的质量浓度误差规律。在此基础上,利用CCD高灵敏度、线性度好等优点,提出一种基于CCD的光散射浓度测量系统,采用一些经典方法去除透射光和杂散光对测量结果的影响,并利用已知孔径的针孔对测量系统进行了校准。最后利用聚苯乙烯小球溶液,对测量系统进行试验评价。
1 散射积分法粉尘质量浓度测量原理
考虑在颗粒粒径连续分布的气固二相流中,在采样区容积VT内,颗粒群的总体积VP,则颗粒群的体积分数 为
为
 (1)
(1)
其中: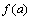 为颗粒粒径分布函数;a为颗粒直径;AL为激光束的截面面积;s为采样长度。式(1)中分子代表采样区内颗粒群的总体积,从随机统计的角度,它实际表示的是颗粒粒径的3阶矩,即颗粒粒径3次方的期望值。若将颗粒的粒径分布函数看成为描述事件出现概率的频率分布函数,则又反映了颗粒粒径3次方的平均值。
为颗粒粒径分布函数;a为颗粒直径;AL为激光束的截面面积;s为采样长度。式(1)中分子代表采样区内颗粒群的总体积,从随机统计的角度,它实际表示的是颗粒粒径的3阶矩,即颗粒粒径3次方的期望值。若将颗粒的粒径分布函数看成为描述事件出现概率的频率分布函数,则又反映了颗粒粒径3次方的平均值。
Fraunhofer衍射理论[14]可以用来描述颗粒的光散射特性。粒径分布为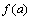 的颗粒群,在不相关单散射的情况下,前向小角范围内散射角为θ处的散射光强
的颗粒群,在不相关单散射的情况下,前向小角范围内散射角为θ处的散射光强 [15]可表示为
[15]可表示为
 (2)
(2)
式中:k=2π/λ,为波数; 为入射激光波长;
为入射激光波长; 为入射光强;J1为第1类Bessel函数。
为入射光强;J1为第1类Bessel函数。
KOO等[16]对颗粒粒径分布的积分变换反演算法进行了研究,发现几种积分变换方法,可以统一写为
 (3)
(3)
式中: ;
;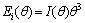 为算法函数;N1为第2类Bessel函数;
为算法函数;N1为第2类Bessel函数;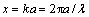 。经过适当的积分变换操作,颗粒群的粒径分布函数
。经过适当的积分变换操作,颗粒群的粒径分布函数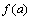 可写为
可写为
 (4)
(4)
采样区域颗粒群的总体积V P的表达式为

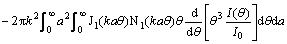 (5)
(5)
从Bessel函数的定义和性质,再经过一定的积分变换[17],可得
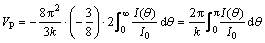 (6)
(6)
由式(6)可以看出:颗粒群的总体积与散射光强在无限空间的角度积分呈正比。考虑到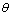 在物理意义上不存在无穷大,其全角积分即为0~π。因此,可获得颗粒体积分数的新的解析表达式为
在物理意义上不存在无穷大,其全角积分即为0~π。因此,可获得颗粒体积分数的新的解析表达式为
 (7)
(7)
由式(7)颗粒体积分数 ,进一步可计算颗粒质量浓度为
,进一步可计算颗粒质量浓度为
 (8)
(8)
式中: 为颗粒质量浓度;
为颗粒质量浓度; 为颗粒的真实密度。
为颗粒的真实密度。
2 散射积分法的数值模拟
散射积分法虽然以Fraunhofer衍射理论为基础,但球形颗粒的光散射的严格数学解是Mie理论,故模拟采用Mie理论计算散射光强。颗粒粒径分布采用Johnson-SB函数[18]模式,此函数能够拟合正态函数、对数正态函数、Rosin-Ranimler分布函数以及修正 函数等,表达式为
函数等,表达式为
 (9)
(9)
其中: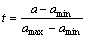 ,a,amax和amin分别为颗粒粒径、粒径范围上限和粒径范围下限;
,a,amax和amin分别为颗粒粒径、粒径范围上限和粒径范围下限; 和μ为分布参数。平均粒径用索太尔平均直径D32表示,具体表达式为
和μ为分布参数。平均粒径用索太尔平均直径D32表示,具体表达式为
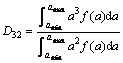 (10)
(10)
式中: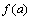 为粒径分布离散值。
为粒径分布离散值。
由角度积分上限和积分上限,导致的颗粒质量浓度相对误差可表示为
 (11)
(11)
式中: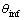 和
和 分别为假定的角度积分下限和积分上限。
分别为假定的角度积分下限和积分上限。
假定 =0.532 μm,粒径分布函数的参数分成3种:
=0.532 μm,粒径分布函数的参数分成3种: =2.5,
=2.5,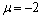 ;
; =2.5,
=2.5, ;
; =4.8,
=4.8, 。折射率m假设为m=1.8非耗散性颗粒和m=1.57-0.56i耗散性颗粒2种情况。图1和图2所示为散射积分法角度积分下限
。折射率m假设为m=1.8非耗散性颗粒和m=1.57-0.56i耗散性颗粒2种情况。图1和图2所示为散射积分法角度积分下限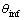 不为0°时的质量浓度相对误差曲线。从图1可以看出:无论是耗散性还是非耗散性颗粒,质量浓度相对误差Δ与
不为0°时的质量浓度相对误差曲线。从图1可以看出:无论是耗散性还是非耗散性颗粒,质量浓度相对误差Δ与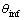 近似呈线性关系,并随着
近似呈线性关系,并随着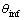 的增加而迅速增大。当
的增加而迅速增大。当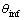 =0.1°时,40 μm平均粒径下的质量浓度相对误差可达到25%,故角度积分下限
=0.1°时,40 μm平均粒径下的质量浓度相对误差可达到25%,故角度积分下限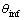 需控制在0.1°以下。从图2可以看出:当
需控制在0.1°以下。从图2可以看出:当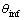 =0.01°时,不同分布参数下同一平均粒径的质量浓度相对误差差距较小,故粒径分布对测量结果影响较小,而平均粒径是影响质量浓度误差最主要的因素,并与质量浓度相对误差近似呈线性关系。另外,不同折射率下的质量浓度相对误差曲线几乎重叠,折射率的类型对质量浓度相对误差的影响可近似忽略。
=0.01°时,不同分布参数下同一平均粒径的质量浓度相对误差差距较小,故粒径分布对测量结果影响较小,而平均粒径是影响质量浓度误差最主要的因素,并与质量浓度相对误差近似呈线性关系。另外,不同折射率下的质量浓度相对误差曲线几乎重叠,折射率的类型对质量浓度相对误差的影响可近似忽略。

图1 θinf≠0°时的积分下限对颗粒质量浓度相对误差的影响
Fig. 1 Effect of lower limit on relative error of dust mass concentration at θinf≠0°

图2 θinf=0.01°时平均粒径对粉尘质量浓度相对误差的影响
Fig. 2 Effect of lower limit on relative error of dust mass concentration at θinf=0.01°
图3和图4所示为角度积分上限 不为π时的质量浓度相对误差。由图3可以看出:当
不为π时的质量浓度相对误差。由图3可以看出:当 在1°~10°内不断增加时,质量浓度相对误差先急剧下降再逐渐平稳趋于定值,当
在1°~10°内不断增加时,质量浓度相对误差先急剧下降再逐渐平稳趋于定值,当 大于5°时,质量浓度相对误差可近似不再降低,故测量系统的散射角接收上限可设定在5°附近;当积分上限
大于5°时,质量浓度相对误差可近似不再降低,故测量系统的散射角接收上限可设定在5°附近;当积分上限 为5°时,不同粒径分布参数对质量浓度相对误差的影响可忽略,而浓度相对误差随着平均粒径的减小而不断增加,当粒径为16 μm时,质量浓度相对误差可达到7%。
为5°时,不同粒径分布参数对质量浓度相对误差的影响可忽略,而浓度相对误差随着平均粒径的减小而不断增加,当粒径为16 μm时,质量浓度相对误差可达到7%。
在实际测量系统中,角度积分下限的大小主要由去除透射光而引起的0°附近散射光无法利用,而角度积分上限则是由散射光收集透镜所能接收的最大散射角决定,而收集透镜对测量区域不同位置的散射光的最大接收角也不同。设定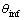 为0.03°,
为0.03°, 在5°~10°时符合实际测量系统的散射光接收角范围。图5所示为积分下限
在5°~10°时符合实际测量系统的散射光接收角范围。图5所示为积分下限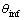 =0.03°,积分上限
=0.03°,积分上限 =5°~10°时,平均粒径D32在20~40 μm的质量浓度相对误差曲线。由图5可见:非耗散性颗粒的质量浓度相对误差约为10%,而耗散性颗粒的质量浓度相对误差近似与粒径呈线性关系并逐渐增加,但在整个粒径范围内均低于非耗散性的质量浓度相对误差,主要由非耗散性颗粒有较多的后向散射光而引起。因质量浓度绝对误差都为正值,质量浓度相对误差浮动相对平稳,所以,通过对实际散射积分区间的光强积分与样品质量浓度的比值进行标定,可以提高测量结果的准确性。
=5°~10°时,平均粒径D32在20~40 μm的质量浓度相对误差曲线。由图5可见:非耗散性颗粒的质量浓度相对误差约为10%,而耗散性颗粒的质量浓度相对误差近似与粒径呈线性关系并逐渐增加,但在整个粒径范围内均低于非耗散性的质量浓度相对误差,主要由非耗散性颗粒有较多的后向散射光而引起。因质量浓度绝对误差都为正值,质量浓度相对误差浮动相对平稳,所以,通过对实际散射积分区间的光强积分与样品质量浓度的比值进行标定,可以提高测量结果的准确性。

图3 θsup≠π时积分上限对粉尘质量浓度相对误差的影响
Fig. 3 Effect of upper limit on relative error of dust mass concentration at θsup≠π
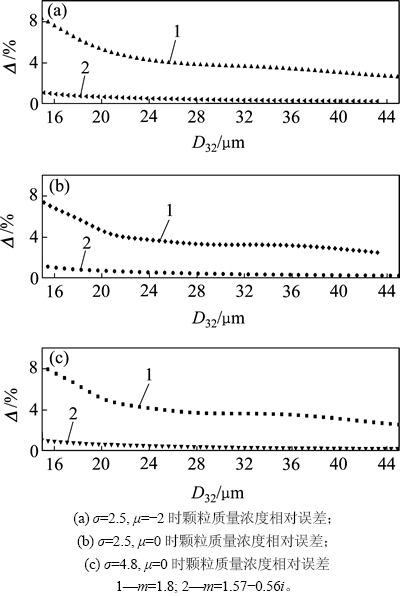
图4 θsup=5°时平均粒径对粉尘质量浓度相对误差的影响
Fig. 4 Effect of mean particle size on relative error of dust mass concentration at θsup=5°
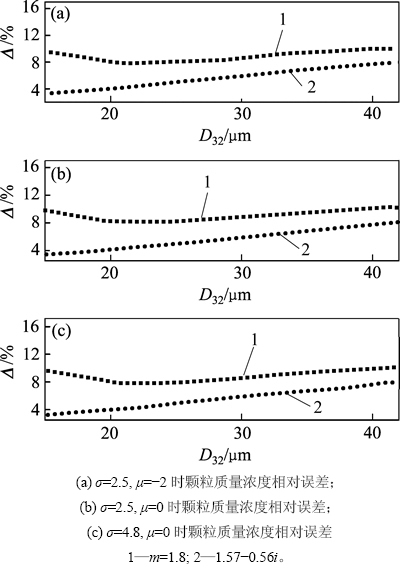
图5 θinf=0.03°和θsup为5°~10°时平均粒径D32对颗粒质量浓度相对误差的影响
Fig. 5 Effect of mean particle diameter D32 on relative error of dust mass concentration at θinf=0.03° and θsup of 5°-10°
3 测量系统及校准试验
3.1 光散射粉尘质量浓度测量系统
图6所示为光散射粉尘浓度测量系统示意图。由图6可以看出:激光器为全固态激光器,波长λ= 0.532 μm,光束直径Dw=1 mm,功率P=30 mW。激光光束经过中性密度滤光片进行光强衰减后进入空间滤波器,空间滤波器由2个平凸透镜(焦距f1=15 mm,f2=60 mm)和1个针孔(孔径Dh=40 μm)组成,可以滤除大部分由激光器产生的杂散光,并对光束进行4倍扩束和准直。图7所示为经滤波器前后的激光器光束截面,其中光强I为光强相对值。由图7可以看出:经过空间滤波器的光束截面附近毛刺消失,光束截面光强曲面更为光滑。测量区域为光程为10 mm的通光石英比色皿,散射光收集透镜(焦距f=60 mm,直径Φ=50.8 mm)置于比色皿后60~80 mm的位置,将测量区域内颗粒的散射光会聚透射到CCD镜头内[19]。45°斜抛的针头反射面放置在收集透镜后焦点处,可将绝大部分中心透射光反射至光收集器。CCD相机感光面为768×576像素点,像素点长×宽为8.30 μm× 8.30 μm,镜头为日本Computar M3514-MP(焦距为 35 mm,光圈为1.4),镜头与相机机身之间加5 mm长度转接环。
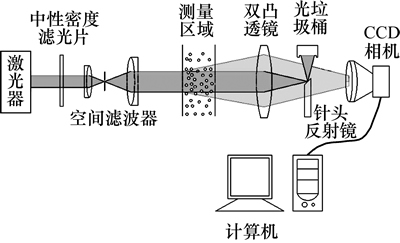
图6 光散射颗粒质量浓度测量系统示意图
Fig. 6 Schematic diagram of light scattering measurement system for dust mass concentration

图7 激光光束截面光强图
Fig. 7 Intensity distribution diagram of laser beam over its cross-section
测量系统中存在的大量杂散光来源于激光器的杂散光、光学系统对光束产生散射和环境光等,除了利用空间滤波器滤除激光器的杂散光、针头反射镜反射透射光到光线收集器外,还可以进行透镜镀膜,测量区域玻璃容器较小角度斜置,在黑暗环境下测量等,以减少杂散光的影响。
3.2 测量系统的校准及线性度验证
将针孔放置在测量区域时,激光光束入射小孔发生衍射,衍射光的光强图进入CCD并计算出光强角分布曲线,与理论情况下的光强角分布曲线对比,并采用一元二次函数对理论光强曲线的角度进行校准以匹配实际光强曲线。首先利用大孔径的针孔D=120 μm和100 μm对测量光路的放大率进行校准,在确定放大率的情况下,利用针孔D=20 μm和40 μm对CCD拍摄图像的角度进行校准[19]。
图8所示为经过校准后的120 μm针孔的光强分布曲线。由图8可知:通过对比Fraunhofer衍射值与试验值,可以确定CCD相机镜头的最大放大率a≈0.3,角度校准公式为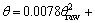
 。因小孔的制造精度限制(孔径绝对误差为±2 μm)以及杂散光的影响,所以,实验值与理论还有一定的偏差。图9所示为20 μm小孔的光强分布曲线。由图9可以看出:CCD可以探测到第3个波峰,但偏差较大,其他峰值被杂散光和暗电流信号淹没。
。因小孔的制造精度限制(孔径绝对误差为±2 μm)以及杂散光的影响,所以,实验值与理论还有一定的偏差。图9所示为20 μm小孔的光强分布曲线。由图9可以看出:CCD可以探测到第3个波峰,但偏差较大,其他峰值被杂散光和暗电流信号淹没。
CCD线性度验证时,通过控制曝光时间ΔT,调节进入CCD的光量。图10所示为当小孔孔径为20 μm时,衍射主峰和第2波峰的光强与曝光时间ΔT的关系。0.3~320 ms的曝光时间内主峰和第2波峰的光强的离散值,与斜率为0.01的直线相比,主峰光强,第2波峰光强值均与曝光时间呈良好的线性关系。线性范围大于2个数量级,这与CCD相机的像素点位深为8位较吻合。

图8 120 μm孔径小孔的衍射光强曲线
Fig. 8 Diffraction pattern of a 120 μm pinhole

图9 20 μm孔径小孔衍射光强曲线
Fig. 9 Diffraction pattern of a 20 μm pinhole

图10 不同曝光时间ΔT下CCD线性度
Fig. 10 CCD linearity with different exposure time
4 颗粒质量浓度试验结果及讨论
为了验证系统对颗粒物质量浓度测量的准确性,实验中采用了国家标准颗粒GBW(E)120004(10 μm)和GBW(E)120006(20 μm)作为样品,悬浮液中聚苯乙烯小球的颗粒数及平均粒径都经光学显微镜直接测量的绝对方法进行标定。首先移除针头,通过透射光的焦点确定散射光中心,然后将加入空白溶液的比色皿放置在测量区域进行背景图像测量,最后测量加入样品的比色皿的散射图像,通过样品散射图像与背景图像的散射光强差,可得悬浮液中小球的散射光强曲线。图11所示为GBW(E)120006(20 μm)样品中小球的散射光强曲线图,离散点为系统测得平均粒径为20 μm的多分散度颗粒群的散射光强,实线为20 μm单分散颗粒的Fraunhofer衍射理论光强曲线。由图11可见:虽然在较大角度上实验光强与理论光强有较大差距,但整体上两者匹配程度较好,并因大角度的散射光强测量相对误差对测量结果的影响远小于极小散射角,故此系统可以满足样品质量浓度的测量的要求。
表1所示为悬浮液中2种标定质量浓度聚苯乙烯小球的实验测量结果。由表1可知:实测质量浓度与标定质量浓度的相对误差基本在15%以内,由于悬浮液中颗粒分布不均匀,以及存在气泡等原因,难免有大的测量质量浓度误差存在,但从整体上看,系统的质量浓度测量结果与标定结果一致性较好。
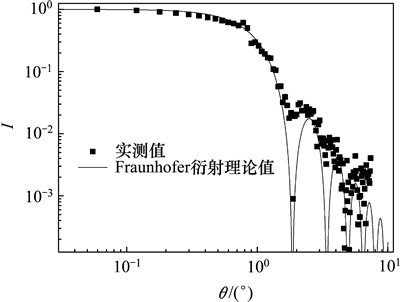
图11 GBW(E)120006(20 μm)样品的颗粒散射光强曲线图
Fig. 11 Scattering intensity curves of sample, GBW(E)120006(20 μm)
表1 2种粒径颗粒的质量浓度测量结果
Table 1 Mass concentration measurements of sample with two particle diameters

5 结论
1) 对利用散射积分法的烟尘质量浓度测量系统进行了误差分析,研究了平均粒径和散射角区间对测量结果的影响,验证了散射积分法无需预知粒径的优点,而当散射角积分为0.03°~5°时就可以满足质量浓度测量需要。
2) 测量系统具有高灵敏度和较好的线性度,线性度范围大于2个数量级,经校准后的衍射光强曲线与理论光强曲线吻合较好。
3) 因样品质量浓度不均匀、存在气泡等原因,导致少量单独测量的质量浓度相对误差较大,但整体上实测值与标定值一致性较好,证明了光散射测量系统的可行性。
参考文献:
[1] JIANG Lili, ZHANG Yunhui, SONG Guixiang. A time series analysis of outdoor air pollution and preterm birth in Shanghai[J]. Biomedical and Environment Sciences, 2007, 20(5): 426-431.
[2] 刘小虎. 粉尘浓度测量技术研究[D]. 西安:西安工业大学电子信息工程学院, 2013: 2-7.
LIU Xiaohu. Study on powder concentration measurement technology[D]. Xi’an: Xi’an Technological University. School of Electronic Information Engineering, 2013: 2-7.
[3] DEGAN G A, PINZARI D L M. Monitoring airborne dust in an Italian basalt quarry: comparison between sampling methods [C]// Air Pollution XXI. Siena, Italy: WIT Press, 2013: 75-84.
[4] AWAD T S, MOHARRAM H A, SHALTOUT O E, et al. Applications of ultrasound in analysis, processing and quality control of food: a review[J]. Food Research International, 2012, 48(2): 410-427.
[5] 王超, 王玉琳, 张文彪. 基于静电传感的气固两相流测量及研究装置[J]. 电子测量与仪器学报, 2011, 25(1): 1-9.
WANG Chao, WANG Yulin, ZHANG Wenbiao. Gas-solid two-phase measurement and research apparatus based on electrostatic sensing[J]. Journal of Electronic Measurement and Instrument, 2011, 25(1): 1-9.
[6] GOBRECHT A, BENDOULA R, ROGER J M, et al. Combining linear polarization spectroscopy and the Representative Layer Theory to measure the Beer–Lambert law absorbance of highly scattering materials[J]. Analytica Chimica Acta, 2015, 853(1): 486-494.
[7] DICK V P. Applicability limits of Beer’s law for dispersion media with a high concentration of particles[J]. Applied Optics, 1998, 37(21): 4998-5004.
[8] HEINISCH R L, BRONOLD F X, FEHSKE H. Mie scattering by a charged dielectric particle[J]. Physical Review Letters, 2012, 109(24): 6380-6383.
[9] 许玉凤. 基于光度计法的粉尘质量浓度测量系统的研究与开发[D]. 南京:南京理工大学理学院, 2007: 11-25.
XU Yufeng. Research and development of the system for dust mass concentration measurement based on photometer measurement[D]. Nanjing: Nanjing University of Science and Technology. School of Science, 2007: 11-25.
[10] 邢键. 基于光后向散射法的烟尘浓度测量技术研究[D]. 哈尔滨:哈尔滨工业大学理学院, 2010: 82-102.
XING Jian. Research on measurement technology of soot concentration based on light backscattering[D]. Harbin: Harbin Institute of Technology. School of Science, 2010: 82-102.
[11] 赵延军. 光散射型颗粒浓度在线监测方法及CEM系统研究[D]. 南京: 东南大学能源与环境学院, 2004: 33-43.
ZHAO Yanjun. Investigation on in-situ measurement of particle concentration by laser scattering[D]. Nanjing: Southeast University. School of Energy and Environment, 2004: 33-43.
[12] LAMANNA G, SUN H, WEIGAND B, et al. Measurements of droplet vaporisation by means of light scattering[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2005, 261(1): 153-161.
[13] BERG M J, HILL S C, GURTON G V A K P. Spatial filtering technique to image and measure two-dimensional near-forward scattering from single particles[J]. Optics Express, 2010, 18(9): 9486-9495.
[14] KHONINA S N, USTINOV A V, KOVALYOV A A, et al. Near-field propagation of vortex beams: models and computation algorithms[J]. Optical Memory and Neural Networks, 2014, 23(2): 50-73.
[15] VAN DE HULST H C. Light scattering by small particles[M]. USA: Dover Publications, 1982: 28-32.
[16] KOO J H, HIRLEMAN E D. Synthesis of integral transform solutions for the reconstruction of particle-size distributions from forward-scattered light[J]. Applied Optics, 1992, 31(12): 2130-2140.
[17] LIU J. Essential parameters in particle sizing by integral transform inversions[J]. Applied Optics, 1997, 36(22): 5535-5545.
[18] YU A B, STANDISH N. A study of particle size distributions[J]. Powder Technology, 1990, 62(2): 101-118.
[19] LEE D, GUTOWSKI I A, BAILEY A E, et al. Investigating the microstructure of a yield-stress fluid by light scattering[J]. Physical Review E, 2011, 83(3): 1-18.
(编辑 刘锦伟)
收稿日期:2015-01-03;修回日期:2015-03-10
基金项目(Foundation item):国家自然科学基金资助项目(51376049);国家质量监督检验检疫总局科技计划项目(2012QK176) (Project(51376049) supported by the National Natural Science Foundation of China; Project(2012QK176) supported by the Science and Technology Development Program of Administration of Quality Supervision, Inspection and Quarantine of People’s Republic of China)
通信作者:许传龙,教授,博士生导师,从事多相流测试技术研究;E-mail: chuanlongxu@seu.edu.cn
摘要:针对散射积分法测量粉尘颗粒质量浓度时,测量系统并不能满足角度积分上限为π和角度下限为0的固有缺陷,基于Mie理论数值计算散射光强的角分布,进而对质量浓度测量误差进行分析。利用电荷耦合元件(charge-coupled device, CCD)的高灵敏度、低噪声、线性度好等优点,研究并搭建一种基于CCD的光散射颗粒质量浓度测量系统,并通过已知孔径的小孔对CCD测量系统的角度分辨率和放大率进行校正,测试CCD的灵敏度及线性度。最后,利用已知粒径和质量浓度的样品对测量系统的准确性进行试验研究。研究结果表明:当散射角积分为0.03°~5°时,可满足质量浓度测量需要,测量相对误差小于15%。
[2] 刘小虎. 粉尘浓度测量技术研究[D]. 西安:西安工业大学电子信息工程学院, 2013: 2-7.
[5] 王超, 王玉琳, 张文彪. 基于静电传感的气固两相流测量及研究装置[J]. 电子测量与仪器学报, 2011, 25(1): 1-9.
[9] 许玉凤. 基于光度计法的粉尘质量浓度测量系统的研究与开发[D]. 南京:南京理工大学理学院, 2007: 11-25.
[10] 邢键. 基于光后向散射法的烟尘浓度测量技术研究[D]. 哈尔滨:哈尔滨工业大学理学院, 2010: 82-102.
[11] 赵延军. 光散射型颗粒浓度在线监测方法及CEM系统研究[D]. 南京: 东南大学能源与环境学院, 2004: 33-43.
[15] VAN DE HULST H C. Light scattering by small particles[M]. USA: Dover Publications, 1982: 28-32.


