Robust control of gantry crane system with hoisting: A new solution based on wave motion
YANG Tang-wen(杨唐文)1, 2, QIN Yong(秦勇)2, HAN Jian-da(韩建达)3
(1. Institute of Information Science, Beijing Jiaotong University, Beijing 100044, China;
2. State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China;
3. State Key Laboratory of Robotics, Shenyang Institute of Automation, Shenyang 110016, China)
Abstract: Large load swing of a gantry crane, due to cable flexibility and rapid movement, needs to be controlled. Herein, a wave-based approach interprets the cable motion as two superposed traveling waves. To combine position and active swing control, the trolley motion and load hoisting are carefully designed here, and a practical approach is adopted to design hoisting motions in the upward and downward manoeuvres, counteracting their reverse effects on the load swing. A robust control algorithm, based on the model of the crane system, is proposed to realize the trolley and hoisting motions, allowing for load variations and parameter uncertainties. This new solution to motion control of a gantry crane works very well, and is stable and adaptive to large load variations. As demonstrated in the simulation experiments, it lands the load rapidly and exactly at target and stops it dead, with nearly zero swing.
Key words: gantry crane systems; robust control; hoisting; mechanical wave concepts
CLC number: TP24 Document code: A Article ID: 1672-7207(2011)S1-0288-05
1 Introduction
A gantry crane system moves a load mass, hanging at the lower end of a soft cable, from an initial position to a target position. In many applications, human operators do the jobs by manual control. However, undesired free pendulum motion, or load swing, is induced due to driver inexperience, causing transfer delays, safety issues and even destructive collisions. Therefore, effective control techniques are needed to manipulate a crane system safely. Gantry crane is a classic example of non-collocated control. That is, the actuator is located distant from the load mass point it is attempting to control, with very loose dynamic coupling, and it must work through the dynamics of the complicated system on its own to control the position of the load mass. To avoid large undesired swings, smaller motion increments and accelerations are frequently used. Consequently, there is an apparent conflict between rapid rest-to-rest motion and the load swing control. Reconciling the two still remains challenging.
For many reasons, it is necessary to ensure minimal load swing on the trolley’s arrival at the target location, particularly as the swing energy and momentum of a heavy load may be very large. Therefore, this issue has attracted much attention over the past decades[1-8]. Starr[1] proposed to stop the swing of a load, hanging at the tip of a PUMA manipulator, by controlling its tip motion. First, the manipulator end-effector is rapidly accelerated from rest to half the maximum transport velocity, which yields only a swing rate but no load swing angle, and then a secondary accelerating step is used to accelerate the load to the maximum velocity at some point where the swing angle and rate are both zero. Constant accelerations are used during the accelerating process. The decelerating motion is just a time-reversed version of the previous accelerating manoeuvre. A swing-free load transport was claimed. Based on the technique, a more general approach was developed further by Jones et al[2] and Strip[8]. A constant-velocity motion is added between the two accelerating steps, so that the demand that the limited acceleration time of the first step be negligible can be removed. A model-free control scheme is proposed to suppress the load swing by Wahyudi et al[9], which comprises of a nominal characteristic trajectory following controller and a fuzzy logic controller.
Wave theories of flexible structures were introduced some twenty years ago (von Flotow[10]). However, in the control area, wave concepts have been avoided, for good reason, generally. Recently, the idea shows potential for vibration control of mechanical systems with flexible structures[3, 7, 11-13]. With this idea, the cable motion of a gantry crane system is interpreted as two elastic waves propagating in opposite directions (launching and returning waves). Matsuda et al[12] used a compensator formulated as an H? optimization to minimise the returning waves at the actuator end. Saigo et al[13] proposed a wave-absorption strategy to suppress vibrations by controlling the lateral motion of the trolley of a suspended pendulum system. Mechanical wave concepts are applied to determine the trolley motion of gantry crane systems without discriminating hoisting motion in Ref.[3]. The wave idea treats vibration in a natural way. It is simple and intuitive, leading to highly efficient and adaptable control for flexible systems.
Usually, a gantry crane moves varying loads, of values unknown to the controller, leading to a very challenging issue of motion control of the gantry crane. Moreover, modeling errors and simplification make the issue more complicated, and the robustness of a control system is difficult to be guaranteed. Sliding mode techniques[14-15] appear to be an effective solution to parameter variations and disturbances. In Ref.[5], an adaptive sliding mode control, using a real-time fuzzy inference, was proposed for an overhead crane. But it is well known that the sliding mode method is prone to suffering from the problematic chattering. Based on the Lyapunov theorem, Lee[6] proposed an anti-swing control law to track planned trajectories, using an approximate linearied model of an overhead crane. Such a linearied model usually ignores important nonlinear dynamics to facilitate controller design. A PD controller with feedback of winch position and velocity (Kiss et al[16]) is used to control a crane, and its stability is proved by the LaSalle's invariance principle. In Ref.[17], nonlinear terms are added to PD controllers to attend the dynamic coupling between the trolley and the load mass. However, in these controllers, the crane models are assumed to be accurate enough, and parameter variations were not taken into account. In this work, a nonlinear control technique is proposed based on a gantry crane model, taking parameter uncertainties into account, especially varying loads.
2 Trolley motion and load mass hoisting
A gantry crane is to move a load rest to rest from an initial to a target location, with hoisting to avoid obstacles. Before the load mass is laid down at target, the load swing is required to be stopped. In Ref.[3], we have analyzed the influence of trolley motion on the load mass swing, based on the wave motion concepts. Here we discuss further the influence of load hoisting on its swing, and then propose in next section a rapid motion control law taking parameter uncertainties into account.
Gantry cranes generally use hoisting, especially for obstacle avoidance in transit. But, empirically we know that hoisting changes the load swing. To study the hoisting effect on the swing, let us analyze the system dynamics first. The dynamics of a crane system is derived here using the Lagrangian formulation by assuming that the load is a lumped mass, the cable is light and straight, and friction and damping are negligible, without loss of generalization, as done in Lee[6], Matsuda et al[12] and Fang et al[17]. Generally, the equations of motion of a gantry crane system can be written in matrix form as[3]
(1)
where 
and 
are given by
,
,
, 
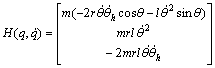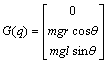and 
,
mt is the equivalent mass of the trolley, and F is the horizontal force to move it. The load m is hanged at the lower end of the cable, and hoisted by the winch, which is fixed on the trolley. Iw and mw are the winch moment of inertia and mass, respectively. r is the winch drum radius, and θh is the winding angle. And thus the hoisting length h(t)=rθh(t). τ is the applied torque to the winch roller, and g is the acceleration due to gravity.
Eliminating the load mass m and the current cable length l=l0-rθh (l0 is the initial length of the cable) from the 3rd equation of the equations of motion, we get
(2)
Eq.(2) describes the relationship among the load swing angle θ and the motions of the trolley y (namely, y(0, t)) and of the winch winding θh. For smaller load swing, as generally happens, Eq.(2) can be further simplified to a second-order, forced vibration equation,
(3)
where ω and ξ are the swing frequency and the damping ratio, respectively, and we have
and 
In Eq.(3), the trolley acceleration is acting as an external forcing function (or an input) to the dynamics of the swinging motion. The transient swing behavior is therefore characterized mainly by the two parameters. The swing frequency, ω, is seen to depend on the hoisting length, while the damping ratio, ξ, depends on both the length and the hoisting rate. When the load mass is being hoisted upwards, the swing frequency increases, while the damping is negative as 
, resulting in an increase in the swing amplitude. When the load mass is hoisted downwards, the swing frequency decreases, 
leads to positive damping. The swing energy is dissipated and the load swing is reduced. Moreover, we can see that the load mass has no direct effect on the swing dynamics.
Taking the different influence of hoisting on the load swing into account, here we set h(t) to be piecewise continuous as
(4)
where tu(<>min) is the time for the upward hoist, and obviously it should be less than the time for the load to hit an obstacle. tmin( ≤ tf) is the minimum time for the trolley to reach the target, which is computed from the target distance and the trolley maximum velocity. tf is the whole manoeuvre time, as defined earlier. hmax is the required hoisting height, and hup(t) and hdn(t) are respectively the reference trajectories to be determined for hoisting up and down.
3 Robust control strategy
Solving 
from Eq. (1), and substituting it into the first one, then the dynamics of the crane system can be written as
(5)
where 
and 
are given by
,
,
,
,
.
Based on the previous equations of motion, an inverse dynamics control law is given by
(6)
where 
is an outer loop of the control, which ensures the stability of the control system.
As we know, in most applications the dynamics parameters of gantry crane systems are variable, and sometimes they are unknown and uncertain. To address the issues, robust control laws are needed, and one is discussed here by
(7)
where 
, 
and 
are the computed versions of 
, 
and 
respectively. They are constant matrices and given a priori. 
is a redesigned outer loop control.
Here, 
comprises of a nominal and error compensating terms, that is
(8)
and v is set as
(9)
where 
, 
, with 
the desired motion vector generated in section 2 and Ref. [3], 
is the actually measured values of the trolley and hoisting motions. Kd and Kp are diagonal positive gain matrices.
is an extra compensating component, used not only to attend the effects of inaccurate or varying parameters on the tracking errors, but also to guarantee stability of the following tracking error equations,
(10)
where
, 
, 
, and 
with 
and 
.
The extra term 
in the control is designed to be the form as
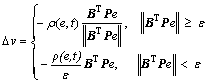(11)
where ε＞0, and P is a positive definite symmetric matrix, which is obtained from
(12)
and A is a Hurwitz matrix, and Q is a specified positive definite symmetric matrix. ρ(e, t) is a boundary function, satisfying 
and 
, and given by
(13)
where K=[Kp, Kd], α, Q1 and β are positive, satisfying the following inequalities:
, 
, and 
,
and 
and γ(e, t) are positive functions of tracking errors and time, respectively satisfying
and 
.
The stability of the proposed control scheme can be proved by the second Lyapunov method. The interested readers please refer Theorem 8.5.3 of Spong et al[18].
4 Simulations
To illustrate the proposed schemes, a crane system with mt=200 kg, mw=100 kg, Iw=20.0 kg·m2 and r=0.2 m, is used for a 12 m manoeuvre. The initial length of the flexible cable is 8.0 m. It is wound to hoist a load mass up and down by 4.0 m, returning to the original height on arrival. The hoisting motion follows a pre-determined polynomial profile, adjusted on line to ensure completion on the trolley's arrival at target. In the proposed control, the traveling distance, the maximum motion speed of the trolley and the hoisting displacement are control parameters, and they are known in advance.
The gantry crane system is designed to handle loads from 1 to 10 t, and the following parameters are used for the robust controller design.
, 
,
, 
Figs.1 and 2 show numerical simulation results for m=1 and 10 t, respectively. The trolley motion and the load hoisting are given in Figs.1(a) and 2(a). The desired values, generated in real time with the planning scheme of section 2 and Ref.[3], are shown with the dashed lines, and the actual motions are given with the solid lines. It can be seen that the trolley stops at the target position precisely and rapidly, and the controller tracks the required trolley and load hoisting motions very well, despite the load variation by a factor of 10. The trolley's velocity profiles shows it moving at close to the maximum velocity for most of the transit time. Figs.1(b) and 2(b) show the swing angles of the load mass respectively. They are almost negligible at the end of the manoeuvres. Although only two simulation cases are studied here, the results well illustrate the excellent performance of the proposed planning and control schemes. Moreover, we can see that the gantry crane takes less time to move smaller load masses by the same distance, which shows that the proposed schemes are flexible, adaptable to the variation of loads.
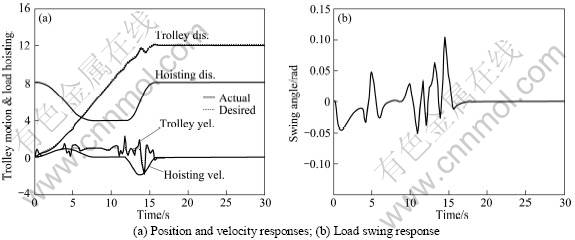
Fig.1 Numerical results for m=1 t
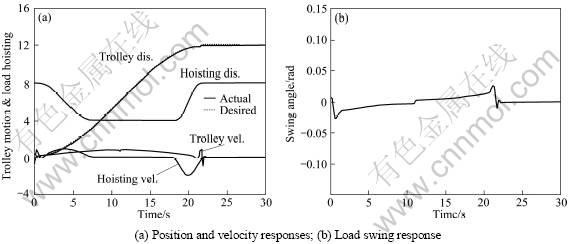
Fig.2 Numerical results for m=10 t
5 Conclusions
A wave based robust control is proposed for an industrial gantry crane system to move varying loads rapidly and precisely. The trolley motion and the load hoisting are designed carefully to avoid load swing. Hoisting effects on the load swing are different in the upward and downward phases, and therefore two different hoisting trajectories are generated in real time. A nonlinear robust control algorithm, based on the dynamics model of the gantry crane system, is adopted to implement the trolley and hoist motions, allowing varying and uncertain parameters. It is demonstrated in the simulation results that, despite load variations, loads can be positioned precisely and rapidly, with nearly zero swing on arrival at target.
References
[1] Starr G P. Swing-free transport of suspended objects with a path-controlled robot manipulator [J]. ASME Journal of Dynamics Systems, Measurement, and Control, 1985, 107: 97-100.
[2] Jones J F, Petterson B J. Oscillation damped movement of suspended objects [C]//Proceedings of IEEE International Conference on Robotics and Automation. Philadelphia, PA, 1988: 956-962.
[3] Yang T W, O'connor W J. Wave-based control for anti-swing motion of a high-speed crane system with hoisting [C]//Proceedings of the IASTED international conference on Robotics and Applications. Cambridge, MA, 2005: 82-87.
[4] Yang T W, O'connor W J. Wave based robust control of a crane system [C]//Proceedings of the IEEE international conference on Intelligent Robots and Systems. Beijing, 2006: 2724-2729.
[5] Liu D T, Yi J Q, Zhao D B, et al. Adaptive sliding mode fuzzy control for a two-dimensional overhead crane [J]. Mechatronics, 2005, 15: 505-522.
[6] Lee H H. A new motion-planning scheme for overhead cranes with high-speed hoist [J]. ASME Journal of Dynamic Systems, Measurement, and Control, 2004, 126: 359-364.
[7] O'connor W J. Wave-based analysis and control of lump-modeled flexible robots [J]. IEEE Transactions on Robotics, 2007, 23(2): 342-352.
[8] Strip D R. Swing-free transport of suspended objects: a general treatment [J]. IEEE Transactions on Robotics and Automation, 1989, 5(2): 234-236.
[9] Wahyudi J J, Muhida R, Salami M J E. Control strategy for automatic gantry crane systems: A practical and intelligent approach [J]. International Journal of Advanced Robotic Systems, 2007, 4(4): 447-456.
[10] von Flotow A H. Traveling wave control for large spacecraft structures [J]. AIAA Journal of Guidance, Control, and Dynamics, 1986, 9: 462-368.
[11] Yang T W, O’connor W J, Ramos F. Wave-based slewing and vibration control of a flexible arm [J]. International Journal of Intelligent Systems Technologies and Applications, 2009, 7(2): 157-160.
[12] Matsuda K, Kanemitsu Y, Kijimoto K. A wave-based controller design for general flexible structures [J]. Journal of Sound and Vibration, 1998, 216(2): 269-279.
[13] Saigo M, Tani K, Usui H. Vibration control of a traveling suspended system using wave absorbing control [J]. ASME Journal of Vibration and Acoustics, 2003, 125: 343-350.
[14] Young K D, Utkin V I, ?zgüner ?. A control engineer's guide to sliding mode control [J]. IEEE Transactions on Control Systems Technology, 1999, 7(3): 328-342.
[15] Bartolini G, Pisano A, Usai E. Second-order sliding-mode control of container cranes [J]. Automatica, 2002, 38(10): 1783-1790.
[16] Kiss B, Lévine J, Mullhaupt P. A simple output feedback PD controller for nonlinear cranes [C]//Proceedings of the IEEE conference on Decision and Control. Sydney, Australia, 2000: 5097-5101.
[17] Fang Y, Dixon W E, Dawson D M, et al. Nonlinear coupling control laws for an underactuated overhead crane system [J]. IEEE-ASME Transactions on Mechtronics, 2003, 8(3): 418-423.
[18] Spong m W, Vidyasagar M. Robot dynamics and control [M]. New York: John Wiley & Sons, 1989: 260-263.
(Edited by YANG You-ping)
Received date: 2011-04-15; Accepted date: 2011-06-15
Foundation item: Project (2011JBM019) supported by the Fundamental Research Funds for the Central Universities; Project (RCS2010K002) supported by the State Key Laboratory of Rail Traffic Control and Safety; Project (RLO200801) supported by State Key Laboratory of Robotics
Corresponding author: YANG Tang-wen, PhD; Tel: +86-10-51684902; E-mail: twyang@bjtu.edu.cn
