J. Cent. South Univ. (2016) 23: 277-285
DOI: 10.1007/s11771-016-3071-7
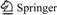
Effect of key factors on cold orbital forging of a spur bevel gear
ZHUANG Wu-hao(庄武豪)1, 2, DONG Li-ying(董丽颖)1, 2
1. School of Materials Science and Engineering, Wuhan University of Technology, Wuhan 430070, China;
2. School of Automotive Engineering, Hubei Key Laboratory of Advanced Technology for Automotive Components, Wuhan University of Technology, Wuhan 430070, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract:
Cold orbital forging is an advanced spur bevel gear forming technology. Generally, the spur bevel gear in the cold orbital forging process is formed by two steps: the preforming step and the final step. Due to the great importance of the final step to gear forming and its complication with interactive factors, this work aims at examining the influence of key factors on the final step in cold orbital forging of a spur bevel gear. Using the finite element (FE) method and control variate method, the influence rules of four key factors, rotation velocity of the upper tool, n, feeding velocity of the lower tool, v, tilted angle of the upper tool, γ, friction factor between the tools and the billet, m, on the geometry and the deformation inhomogeneity of the cold orbital forged gear are thoroughly clarified. The research results show that the flash becomes more homogeneous with increasing v, increasing m, decreasing n or decreasing γ. And the deformation of the gear becomes more homogeneous with increasing v, decreasing n or decreasing γ. Finally, a corresponding experiment is conducted, which verifies the accuracy of FE simulation conclusions.
Key words:
cold orbital forging; FE modeling; key factors; spur bevel gears;
1 Introduction
As an incremental metal forming process, cold orbital forging is widely used to produce spur bevel gears. A representative of the cold orbital forging process is vividly shown in Fig. 1. As can be seen, the conical upper tool is tilted by angle γ and it continually rotates around the vertical machine axis with the constant rotation velocity n. At the same time, the lower tool feeds to press the billet vertically with the feeding velocity v. Under these actions of the tools, the billet deforms locally and continuously. From the above description, it can be inferred that the cold orbital forging process is very complicated with interactive factors.
In retrospect, many scholars have studied the orbital forging process for its outstanding features such as high accuracy, low vibration and significant materials saving. Summarily, these studies have been centered on cylindrical and ring billets, including analyzing the contact behaviors [1-5], calculating the power [6-11], testing the plastic deformation behaviors [12-19] and forecasting the forming defects [20-22]. It should be pointed out that the aforementioned studies are limited to simple geometries. However, the gears which belong to the complex geometries are traditionally investigated by the conventional forging [23-24], cold closed-die forging [25-27] and rotational fine blanking [28] while they are scantly investigated by orbital forging. Deng et al [29] simulated the cold orbital forging process of a spur bevel gear and optimized the billet geometry. Han et al [30] investigated the process design and control method in cold rotary forging of gears with non-rotary upper and lower profiles.  [31] accomplished the simulation of the complex motion of the rocking tool in cold orbital forging. Noticeably, these studies focus on one-step formation in cold orbital forging of spur bevel gears, which is theoretical. In fact, spur bevel gears in the cold orbital forging process are commonly formed by two steps in the actual production. This is because cold orbital forging of spur bevel gears with two steps can not only reduce the forging force and prolong the life of the tools but also make the metal redistribute to fill the tool cavities better. Therefore, this work investigates the cold orbital forging of spur bevel gears with two steps.
[31] accomplished the simulation of the complex motion of the rocking tool in cold orbital forging. Noticeably, these studies focus on one-step formation in cold orbital forging of spur bevel gears, which is theoretical. In fact, spur bevel gears in the cold orbital forging process are commonly formed by two steps in the actual production. This is because cold orbital forging of spur bevel gears with two steps can not only reduce the forging force and prolong the life of the tools but also make the metal redistribute to fill the tool cavities better. Therefore, this work investigates the cold orbital forging of spur bevel gears with two steps.
Due to the great importance of the final step to gear forming and its complication with interactive factors, this work aims at examining the influence of key factors on the final step in cold orbital forging of a spur bevel gear. According to the practical geometry shape and dimensions, the FE model in Deform-3D software is established. Through the FE model, the influence rules of the four key factors, rotation velocity of the upper tool n, feeding velocity of the lower tool v, tilted angle of the upper tool γ, friction factor between the tools and the billet m, on the geometry and the deformation inhomogeneity of the cold orbital forged gear are thoroughly clarified.
2 FE models of cold orbital forging of a spur bevel gear
In this work, the FE method is adopted to examine the influence rules of four key factors on the final step in cold orbital forging of the 20CrMnTi alloy spur bevel gear. As the initial billet in the final step is obtained from the final stage of the first step, the two FE models of the upper tool, lower tool and the billet are established in accordance with the practical geometry shape and dimensions, as shown in Fig. 2. After the achievement of the geometry models, the billet and tools are assembled in the global coordinate system. The tools are defined as the analytical rigid bodies while the billets are defined as deforming solid bodies with the element numbers 60538 and 100986 (the preforming step and the final step), respectively. The model of the friction is shear and the size of time-step is 0.02.
3 Results and discussion
In view of the FE models above, the influence rules of cold orbital forging of a spur bevel gear in the final step are thoroughly clarified by analyzing the influence of the key factors, rotation velocity of the upper tool n, feeding velocity of the lower tool v, tilted angle of the upper tool γ, friction factor between the tools and the billet m, on the geometry and the deformation inhomogeneity of the cold orbital forged gear.
3.1 Calculation parameters
Parameter 1 includes n={20, 30, 40, 60, 120, 240, 480} (r/min), v=5 mm/s, γ=1.5° and m=0.14. This is aimed to examine the influence of rotation velocity of the upper tool n on the final step.
Parameter 2 includes v={0.625, 1.25, 2.5, 5, 7.5, 10, 15} (mm/s), n=60 r/min, γ=1.5° and m=0.14. This is aimed to examine the influences of feeding velocity of the lower tool v on the final step.
Parameter 3 includes γ={0.25, 1, 2, 3, 4, 6, 8} (°), v={2.5, 5, 10} (mm/s), n=60 r/min and m=0.14. This is aimed to examine the influence of tilted angle of the upper tool γ on the final step.
Parameter 4 includes m={0.05, 0.1, 0.14, 0.3, 0.4, 0.5, 0.7}, v={2.5, 5, 10} (mm/s), n=60 r/min and γ=1.5°. This is aimed to examine the influence of friction factor between the tools and the billet m on the final step.
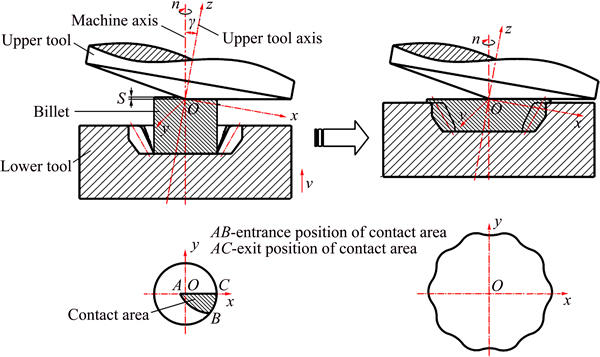
Fig. 1 forming principle of cold orbital forging

Fig. 2 FE models of cold orbital forging of spur bevel gear with two steps:
3.2 Influence of key factors on geometry of cold orbital forged gear
As the cold orbital forging process of the spur bevel gear reaches the final stage, the flash is gradually formed, as shown in Fig. 3. The size of the flash changes greatly with different key factors. When the size of the flash is larger, more metal flows into the flash region and less metal flows into the tool cavities correspondingly, leading to the difficulty in the tool cavities filling, and vice versa. As a consequence of this, the maximum and the minimum radii of the flash can be regarded as important indexes for the geometry of the cold orbital forged gear. Noticeably, when the metal flows out of the tool cavity in the radial direction, the resistants of metal flow in the directions of addendum and dedendum are different, leading to the inhomogeneity of the flash. Then, φ (φ=Rmax-Rmin) is defined as another index for the geometry of the cold orbital forged gear, which is also shown in Fig. 3. Obviously, the flash becomes more inhomogeneous with the larger value of φ, and vice versa.
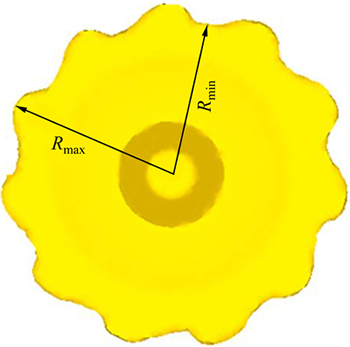
Fig. 3 geometry and measurement of flash (inhomogeneity of flash: φ=Rmax-Rmin; Rmax: the maximum radius of flash; Rmin: the minimum radius of the flash)
Figure 4 shows the influence of n and v on the geometry of the cold orbital forged gear, namely the influence on the maximum and the minimum radii of the flash. It is interesting to find that if S (S=60v/n, which is defined as feeding amount per rotation) is constant and whichever n or v changes, the maximum and the minimum radii of the flash are substantially unchanged. That is to say, the influences of n and v on the size of the flash can be regarded as the influence of S. With increasing S, both the maximum and the minimum radii of the flash are decreasing. This indicates that the increase of S makes the metal easier to fill the tool cavities. This can be explained as follows. When S is small, the deformation mainly occurs in the region near the upper surface of the billet and the “mushroom” effect becomes obvious, leading to a large flash. With increasing S,the deformation of the billet from upper surface to lower surface is more homogeneous and the “mushroom” effect becomes less obvious [15]. As a consequence, the size of the flash in the cold orbital forged spur bevel gears decreases and the tool cavity can be filled perfectly. Noticeably, the lines in Fig. 4 decrease sharply when S is smaller than 5 mm/r and quite slowly when S is larger than 5 mm/r.
Fig. 4 Effects of n and v on geometry of cold orbital forged gear:
Figure 5 shows the influence of S on the inhomogeneity of the flash in the cold orbital forged spur bevel gears. In this figure, the value of φ decreases with increasing S. That is to say, the flash becomes more homogeneous with increasing S. The lines in Fig. 5 also decrease slowly when S is larger than 5 mm/r. Figure 6 shows the deformation of the flash in the cold orbital forged spur bevel gears for different S. When S is 0.625 mm/r, the difference of the flash between the maximum radius and the minimum one is the largest, leading to the inhomogeneous flash. However, when S reaches 15 mm/r, the maximum radius and the minimum one of the flash are almost the same, leading to the homogeneous flash.

Fig. 5 Effects of S on inhomogeneity of flash of cold orbital forged gear

Fig. 6 deformation of flash of cold orbital forged gear for different S:
Figure 7 shows the interactive influence of γ and S on the geometry of the cold orbital forged gear. In fig. 7, the maximum and the minimum radii of the flash are increasing with increasing γ for a constant S. It indicates that more metal flows out of the tool cavity and forms the flash. That is to say, it is more difficult to completely fill the tool cavity with increasing γ. This is because with the increase of γ, the plastic deformation area mainly occurs in the upper surface of the billet and a more obvious “mushroom” effect occurs, leading to a larger radius of the flash. From Fig. 7, it can also be seen that a larger S can produce a smaller radius of the flash, which is in agreement with Fig. 4. And the maximum radius of the flash increases more rapidly than the minimum one with increasing γ, thus leading to the increase of φ, namely the flash becomes more inhomogeneous, as shown in Figs. 8 and 9. In addition, Fig. 7 illustrates that φ decreases with increasing S for a constant γ, which is in agreement with Fig. 5.
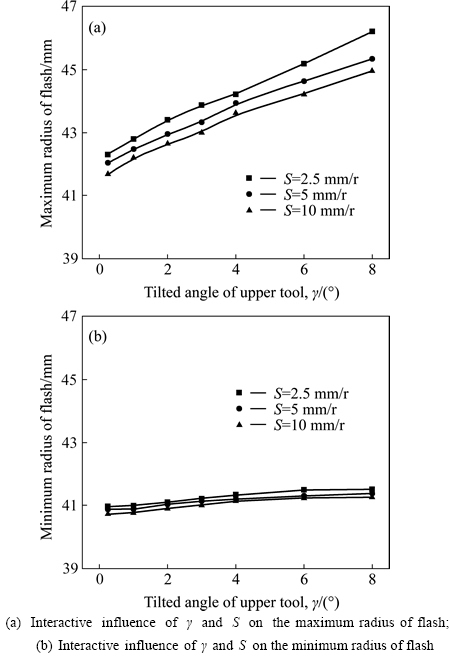
Fig. 7 interactive effects of γ and S on geometry of cold orbital forged gear:
Figure 10 shows the interactive influences of m and S on the geometry of the cold orbital forged gear. In this figure, the maximum radius of the flash is decreasing while the minimum one is increasing with increasing m.
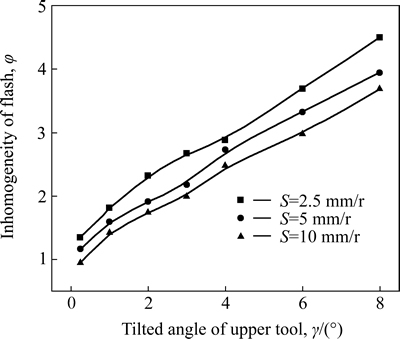
Fig. 8 interactive influences of γ and S on inhomogeneity of flash of cold orbital forged gear
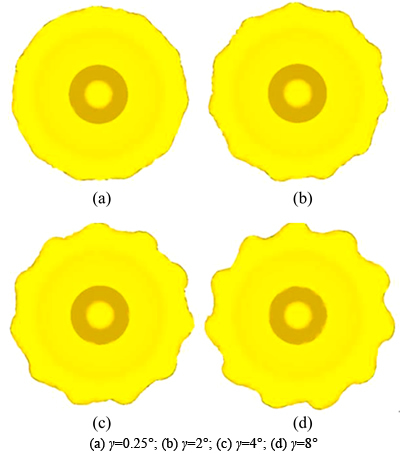
Fig. 9 deformation of flash of cold orbital forged gear for different γ:
Figure 11 shows the interactive influences of m and S on the inhomogeneity of the flash of the cold orbital forged gear. In this figure, φ decreases with increasing m, namely the flash becomes more homogeneous. Moreover, Fig. 11 also shows that for a constant m, φ decreases with increasing S, which is in agreement with Fig. 5. The deformation of the flash of the cold orbital forged gear for different m is shown in Fig. 12. When m is 0.05, the difference between the maximum radius and the minimum one is the largest, leading to the most inhomogeneous flash. When m increases to 0.7, the difference between the maximum radius and the minimum one is quite small, leading to the most homogeneous flash.
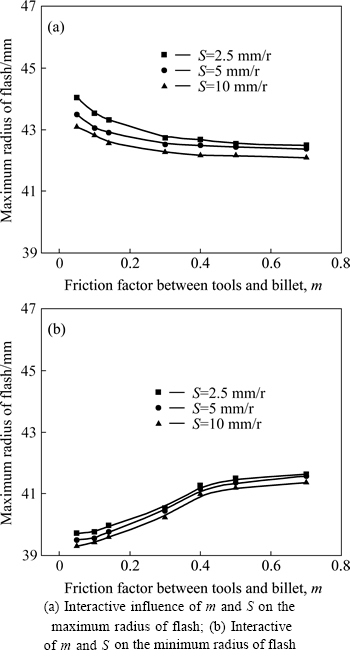
Fig. 10 interactive effects of m and S on geometry of cold orbital forged gear:

Fig. 11 interactive effects of m and S on inhomogeneity of flash of cold orbital forged gear
3.3 Influence of key factors on deformation inhomogeneity of cold orbital forged gear
As cold orbital forging is an incremental metal forming process, the metal undergoes different deformation degree. That is to say, the deformation ofthe cold rotary forged gear is inhomogeneous after cold orbital forging process. The inhomogeneity of the cold orbital forged gear can highly affect its performance. Therefore, the standard deviation of the effective strain is adopted as an important index for the deformation inhomogeneity of the cold orbital forged gear. Figure 13 shows the distribution of the effective strain of the cold orbital forged gear. Obviously, the deformation of the gear is inhomogeneous and the most inhomogeneous area is on the surface of the gear.
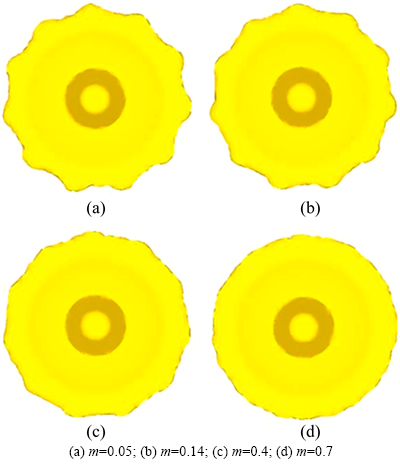
Fig. 12 deformation of flash of cold orbital forged gear for different m:

Fig. 13 distribution of effective strain of cold orbital forged gear
Figure 14 shows the influences of n and v on the deformation inhomogeneity of the cold orbital forged gear, namely the influence on the standard deviation of the effective strain. In this figure, two lines almost overlap together which infers that the influence of n and v on the deformation inhomogeneity of the cold orbital forged gear can be attributed to the influence of S. With increasing S, the standard deviation of the effective strain gradually decreases. This is mainly because when S is smaller, the deformation mainly occurs on the upper surface of the billet and the metal in this region flows out of the tool cavities to form larger flash (shown in Fig. 4). However, when S is larger, the metal in the upper and lower surface deforms simultaneously. This makes the deformation of the gear more homogeneous and the standard deviation of the effective strain smaller accordingly. Noticeably, the lines in Fig. 14 decrease sharply when S is smaller than 5 mm/r and quite slowly when S is larger than 5 mm/r.
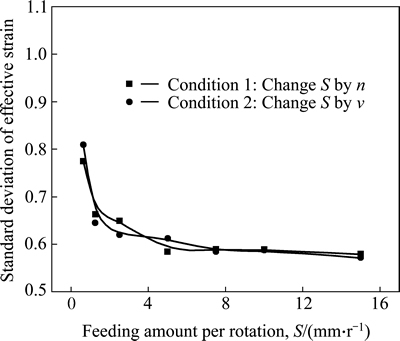
Fig. 14 Effects of n and v on deformation inhomogeneity of cold orbital forged gear
Figure 15 shows the interactive influences of γ and S on the deformation inhomogeneity of the cold orbital forged gear. In this figure, the standard deviation increases with increasing γ for a constant S. This is because with a larger γ, the deformation mainly occurs on the upper surface of the billet, where a larger flash is formed (shown in Fig. 7), leading to the inhomogeneity of the cold orbital forged gear. From Fig. 15, it can also be seen that a larger S can produce a smaller standard deviation of the effective strain, which is in agreement with Fig. 14.
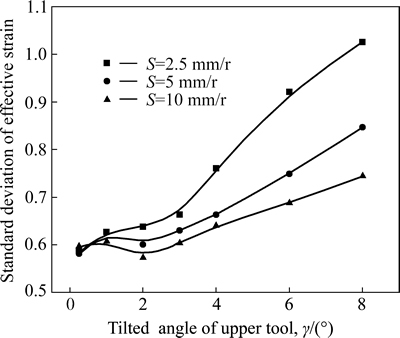
Fig. 15 interactive effects of γ and S on deformation inhomogeneity of cold orbital forged gear
Figure 16 shows the interactive influence of m and S on the deformation inhomogeneity of the cold orbital forged gear. In this figure, the standard deviation is relatively steady with increasing m for a constant S. That is to say, m has little influence on the deformation inhomogeneity of the cold orbital forged gear. The reason can be as follows: The metal flow resistant between the billet and tools increases with increasing m, leading to the larger deformation on the surface of the gear. With the proceeding of the cold orbital forging process, this deformation area can easily permeate into the center of the gear and make the deformation of the gear homogeneous. From Fig. 16, it can also be seen that a larger S can produce a smaller standard deviation of the effective strain, which is in agreement with Fig. 14.
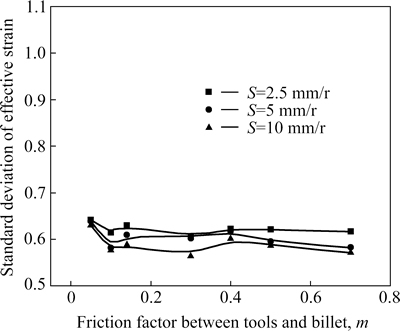
Fig. 16 interactive effects of m and S on deformation inhomogeneity of cold orbital forged gear
3.4 Validation of FE models of cold orbital forging
For the consideration of the analysis above and the practical working condition, the optimized parameters are selected and used for simulation, as listed in Table 1. The simulative results with different strokes of the billet are achieved, which is shown in Fig. 17. In this figure, the spur bevel gear is gradually formed with undistorted mesh in the cold orbital forging process.
In order to evaluate the accuracy of the proposed FE model, the experiments with the same parameters are carried out. In these experiments, the material of the billet is 20CrMnTi alloy which is under isothermal spheroidization and the lubricant is MoS2.
Table 1 Simulative parameters for FE models

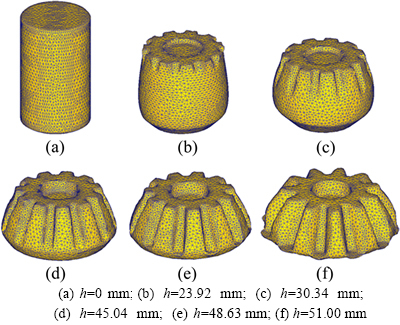
Fig. 17 Spur bevel gear formed with undistorted mesh in cold orbital forging process (h: stroke of lower tool):
It is known that the shape of the billet plays an important role in the comparison between the experimental results and the simulative ones after the cold orbital forging process. Figure 18 shows the deformed billet in the final stage of the two steps. From Fig. 18, there is a good consistency on the gear shape between experimental and simulative results. In view of the above analysis, the proposed models of cold orbital forging are proved to be reliable experimentally and the selected parameters can be used to form the spur bevel gear perfectly.

Fig. 18 billet deformed in each step after experiments (a) and simulations (b)
4 Conclusions
1) The key factors have great influence on the geometry of the cold orbital forged gear. The influences of n and v on the size of the flash can be regarded as the influence of S. With increasing S, both the maximum and the minimum radii of the flash are decreasing, leading to the metal easier to fill the tool cavities. And the flash becomes more homogeneous with increasing S. With increasing γ, the maximum and the minimum radii of the flash are increasing, which makes the metal more difficult to completely fill the tool cavity. And the flash becomes more inhomogeneous with increasing γ. With increasing m, the maximum radius of the flash is decreasing while the minimum one is increasing. And the flash becomes more homogeneous with increasing m.
2) The key factors have great influence on the deformation inhomogeneity of the cold orbital forged gear. The influences of n and v on the deformation inhomogeneity of the cold orbital forged gear can be attributed to the influence of S. With increasing S, the standard deviation of the effective strain is smaller and the deformation of the gear is more homogeneous accordingly. With increasing γ, the standard deviation of the effective strain increases, leading to the inhomogeneity of the cold orbital forged gear. With increasing m, the standard deviation is relatively steady. That is to say, m has little influence on the deformation inhomogeneity of the cold orbital forged gear.
3) In order to evaluate the accuracy of the proposed FE model and the optimized parameters, the simulation and the experiment with the same parameters are carried out. The results show that the proposed models of cold orbital forging are proved to be reliable experimentally and the selected parameters can be used to form the spur bevel gear perfectly with two steps.
References
[1] Hawkyard J B, Gurnani C K S, Johnson W. Pressure-distribution measurements in rotary forging [J]. Journal of Mechanical Engineering Science, 1977, 19: 135-142.
[2] Pei X H, Zhou D C, Wang Z R. Some basic problems of the rotary forging and its application [C]// Proceedings of the second International Conference on Rotary Metalworking Processes. 1982: 81-90.
[3] HAN Xing-hui, HUA Lin. Prediction of contact pressure, slip distance and wear in cold rotary forging using finite element methods [J]. Tribology International, 2011, 44 (12): 1742-1753.
[4] HAN Xing-hui, HUA Lin. Investigation on contact parameters in cold rotary forging using a 3D FE method [J]. International Journal of Advanced Manufacturing Technology, 2012, 62 (9/10/11/12): 1087-1106.
[5] HAN Xing-hui, HUA Lin. 3D FE modelling of contact pressure response in cold rotary forging [J]. Tribology International, 2013, 57: 115-123.
[6] APPLETON E, SLATER R A C. Effects of upper platen configuration in the rotary forging process and rotary forging into a contoured lower platen [J]. International Journal of Machine Tool Design and Research, 1973, 13(1): 43-62.
[7] ZHANG Meng. Calculating force and energy during rotary forging [C]// Proceedings of the Third International Conference on Rotary Metalworking Processes. 1984: 115-124.
[8] OUDIN J, RAVALARD Y, VERWAERDE G, GELIN J C. Force, torque and plastic flow analysis in rotary upsetting of ring shaped billets [J]. International Journal of Mechanical Sciences, 1985, 27(11/12): 761-780.
[9] HAWKYARD J B, SMITH C P. The influence of elastic die distortion on forming force in rotary forging [J]. International Journal of Mechanical Sciences, 1988, 30(8): 533-542.
[10] CANTA T, FRUNZA D, SABADUS D, TINTELECAN C. Some aspects of energy distribution in rotary forming processes [J]. Journal of Materials Processing Technology, 1998, 80/81: 195-198.
[11] ZHOU De-cheng, HAN Ya-dong, WANG Z R. Research on rotary forging and its distribution of deformation [J]. Journal of Materials Processing Technology, 1992, 31(1/2): 161-168.
[12] CHOI S, NA K H, KIM J H. Upper-bound analysis of the rotary forging of a cylindrical billet [J]. Journal of Materials Processing Technology, 1997, 67(1): 78-82.
[13] KALINOWSKA-OZGOWICZ E, KRUKIEWICZ W, KOWALSKI L, KOZIK R, RABUS J, SZOTA J G. Orbital forming of an oxygen cylinder web [J]. Journal of Materials Processing Technology, 1997, 64(1): 215-222.
[14] WANG Guang-chun, GUAN Jing, ZHAO Guo-qun. A photo-plastic experimental study on deformation of rotary forging a ring workpiece [J]. Journal of Materials Processing Technology, 2005, 169(1): 108-114.
[15] HUA Lin, HAN Xing-hui. 3D FE modeling simulation of cold rotary forging of a cylinder workpiece [J]. Materials and Design, 2009, 30(6): 2133-2142.
[16] HAN Xing-hui, HUA Lin. Effect of size of the cylindrical workpiece on the cold rotary-forging process [J]. Materials and Design, 2009, 30(8): 2802-2812.
[17] HAN Xing-hui, HUA Lin. 3D FE modeling of cold rotary forging of a ring workpiece [J]. Journal of Materials Processing Technology, 2009, 209(12/13): 5353-5362.
[18] HAN Xing-hui, HUA Lin. Comparison between cold rotary forging and conventional forging [J]. Journal of Mechanical Science and Technology, 2009, 23(10): 2668-2678.
[19] LIU G, YUAN S J, WANG Z R, ZHOU D C. Explanation of the mushroom effect in the rotary forging of a cylinder [J]. Journal of Materials Processing Technology, 2004, 151(1/2/3): 178-182.
[20] ZHOU De-cheng, YUAN Shi-jian, WANG Z R, XIAO Zhen-rui. Defects caused in forming process of rotary forged parts and their preventive methods [J]. Journal of Materials Processing Technology, 1992, 32(1/2): 471-479.
[21] OH H K, CHOI S. Ductile fracture in the central region of a circular plate in rotary forging [J]. Journal of Materials Processing Technology, 1997, 68(1): 23-26.
[22] OH H K, CHOI S. A study on center thinning in the rotary forging of a circular plate [J]. Journal of Materials Processing Technology, 1997, 66(1): 101-106.
[23] LEE J J, JUNG U J, PARK G J. Shape optimization of the workpiece in the forging process using equivalent static loads [J]. Finite Elements in Analysis and Design, 2013, 69: 1-18.
[24] BRINKSMEIER E, LUBBEN T, FRITSCHING U, CUI Cheng-song, RENTSCH R, SOLTER J. Distortion minimization of disks for gear manufacture [J]. International Journal of Machine Tools and Manufacture, 2011, 51(4): 331-338.
[25] SONG J H, IM Y T. Process design for closed-die forging of bevel gear by finite element analyses [J]. Journal of Materials Processing Technology, 2007, 192/193: 1-7.
[26] HU Cheng-liang, WANG Ke-sheng, LIU Quan-kun. Study on a new technological scheme for cold forging of spur gears [J]. Journal of Materials Processing Technology, 2007, 187/188: 600-603.
[27] JIN Jun-song, XIA Ju-chen, WANG Xin-yun, HU Guo-an, LIU Hua. Die design for cold precision forging of bevel gear based on finite element method [J]. Journal of Central South University of Technology, 2009, 16(4): 546-551.
[28] YANG Shan, SONG Yan-li, ZHANG Mei. Effects of parameters on rotational fine blanking of helical gears [J]. Journal of Central South University, 2014, 21(1): 50-57.
[29] DENG Xiao-bin, HUA Lin, HAN Xing-hui, SONG Yan-li. Numerical and experimental investigation of cold rotary forging of a 20CrMnTi alloy spur bevel gear [J]. Materials and Design, 2011, 32(3): 1376-1389.
[30] HAN Xing-hui, HUA Lin, ZHUANG Wu-hao, ZHANG Xin-chang. Process design and control in cold rotary forging of non-rotary gear parts [J]. Journal of Materials Processing Technology, 2014, 214(11): 2402-2416.
[31]  G. Investigation of the cold orbital forging process of an AlMgSi alloy bevel gear [J]. Journal of Materials Processing Technology, 2013, 213(10): 1692-1702.
G. Investigation of the cold orbital forging process of an AlMgSi alloy bevel gear [J]. Journal of Materials Processing Technology, 2013, 213(10): 1692-1702.
(Edited by YANG Hua)
Foundation item: Project(51105287) supported by the National Natural Science Foundation of China; Project(IRT13087) supported by Innovative Research Team Development Program of Ministry of Education of China; Project(2012-86) supported by High-End Talent Leading Program of Hubei Province, China; Project(2014CFB876) supported by Natural Science Foundation of Hubei Province, China
Received date: 2014-12-02; Accepted date: 2015-04-10
Corresponding author: DONG Li-ying, Master; Tel: +86-27-87168391; E-mail: dongliying99@163.com
Abstract: Cold orbital forging is an advanced spur bevel gear forming technology. Generally, the spur bevel gear in the cold orbital forging process is formed by two steps: the preforming step and the final step. Due to the great importance of the final step to gear forming and its complication with interactive factors, this work aims at examining the influence of key factors on the final step in cold orbital forging of a spur bevel gear. Using the finite element (FE) method and control variate method, the influence rules of four key factors, rotation velocity of the upper tool, n, feeding velocity of the lower tool, v, tilted angle of the upper tool, γ, friction factor between the tools and the billet, m, on the geometry and the deformation inhomogeneity of the cold orbital forged gear are thoroughly clarified. The research results show that the flash becomes more homogeneous with increasing v, increasing m, decreasing n or decreasing γ. And the deformation of the gear becomes more homogeneous with increasing v, decreasing n or decreasing γ. Finally, a corresponding experiment is conducted, which verifies the accuracy of FE simulation conclusions.


