Trans. Nonferrous Met. Soc. China 24(2014) 1458-1466
Compositional optimization of glass forming alloys based on critical dimension by using artificial neural network
An-hui CAI1,2, Xiang XIONG2, Yong LIU2, Wei-ke AN1, Guo-jun ZHOU1, Yun LUO1, Tie-lin LI1, Xiao-song LI1, Xiang-fu TAN1
1. College of Mechanical Engineering, Hunan Institute of Science and Technology, Yueyang 414000, China;
2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China
Received 25 June 2013; accepted 30 October 2013
Abstract:
An artificial neural network (ANN) model was developed for simulating and predicting critical dimension dc of glass forming alloys. A group of Zr-Al-Ni-Cu and Cu-Zr-Ti-Ni bulk metallic glasses were designed based on the dc and their dc values were predicted by the ANN model. Zr-Al-Ni-Cu and Cu-Zr-Ti-Ni bulk metallic glasses were prepared by injecting into copper mold. The amorphous structures and the determination of the dc of as-cast alloys were ascertained using X-ray diffraction. The results show that the predicted dc values of glass forming alloys are in agreement with the corresponding experimental values. Thus the developed ANN model is reliable and adequate for designing the composition and predicting the dc of glass forming alloy.
Key words:
critical dimension; glass forming alloy; artificial neural network; metallic glasses;
1 Introduction
Metallic glasses have drawn a lot of interests because of their superior physical, mechanical and chemical properties compared with the corresponding crystalline counterparts [1,2]. In particular, the development of bulk metallic glasses (BMGs) widens their applications and extensively triggers the investigation of glass forming ability (GFA) of alloys.
There are many methods for estimating the GFA of glass forming alloys. One includes empirical rule proposed by INOUE and ZHANG [3] and the electron concentration rule proposed by CHEN et al [4]. These rules can not quantitatively estimate the GFA of the alloys and even there are opposite cases [5]. The second method is the characterization parameters, such as Kgl [6], △Tx [7], Trg [8,9], γ [7, 9], γ* [10] and ν [11]. These parameters can be obtained after the amorphous alloy has been prepared and/or even there are opposite cases [12]. The third method is the mathematical and/or physical equation [9,13-16]. For example, INOUE et al [15] provided an equation for the estimation of critical cooling rate Rc. LU and LIU [9,16] proposed some empirical relationships for the prediction of the Rc. However, the equation includes some parameters which are difficult to obtain and/or their reliability depends on the number of the data. CAI et al [17,18] tried to relate the Rc with the physical and/or chemical parameters. Although better results were obtained and these parameters were also easily calculated, these relationships can not characterize in the commonality. Finally, researchers proposed some models from the thermal, topological and physical points of view. For example, the composition located at deep eutectic point was designed by thermodynamics [19]. It is clear that its result would deviate from the practical case because the formation of the metallic glass is a non-equilibrium solidification procedure. From the topological structure, it was found that the atomic size ratio [20], the average electronegativity difference [21], and the local packing efficiency [22] were strongly related with the GFA of alloys. However, these parameters are difficult to be calculated for the multi-component alloy. PANG et al [23] have recently designed the composition of Ni-Hf amorphous alloys based on the cluster whose type and magnitude are difficult to be defined. GUO and LIU [24], and CAI et al [25] have recently estimated the Rc for the formation of amorphous alloys from the dc from the thermodynamic point of view. However, the thermodynamic model contains many parameters which are difficult to be measured and depend on the temperature. Among above mentioned parameters, the dc can be directly used to evaluate the GFA of glass forming alloys. However, the dc of the glass forming alloy can be obtained through a large number of the experiments and depends on the experimental condition. Can it be quickly and reliably estimated ahead of the experiments?
It is well known that the dc is influenced by physical and chemical factors. The relationships between the dc and these factors are very complex, resulting in the difficult description of the relationships by a mathematical and/or physical model. Artificial neural network (ANN) technique is thought to be a reliable method for the resolution of the complex system and has been effectively used for the composition design, technology optimization, and performance prediction [26-33] due to its perfect performance, such as self-organization, self-adaption, strong learning and anti-interference capacity. Moreover, the ANN technique has been used to predict parameters for the metallic glasses and reliable results are obtained. For example, KEONG et al [34] established an ANN model for reliably predicting the crystallization temperatures of the Ni-P based metallic glasses. CAI et al [35-37] established ANN models for predicting Trg, △Tx and Rc of glass forming alloy, respectively. But there are no reports for the prediction of the dc of glass forming alloy by ANN technique.
In the present work, a computer model based on radial basis function artificial neural network (RBFANN) is designed for prediction and simulation of the dc of metallic glass. In addition, a group of Zr-Al-Ni-Cu bulk metallic glasses are designed and their dc values are predicted by the RBFANN model. It is found that the predicted dc values are in good agreement with the corresponding experimental values.
2 Experimental
Zr-Al-Cu-Ni and Cu-Zr-Ti-Ni shown in Tables 1 and 2 alloys with nominal compositions (mole fraction, %) were pre-alloyed more than five times by arc melting pure metal elements in a Ti-gettered argon atmosphere. These master ingots then were surface-polished, followed by induction-melting inside quartz tubes in argon atmosphere, then injected into copper mold to obtain d1-10 mm conical samples. The amorphous structures and the determination of the dc of as-cast alloys were ascertained using X-ray diffraction (XRD) with a XD-3A diffractometer with Cu Kα.
Table 1 Predicted and tested dc values for Zr-Al-Ni-Cu bulk metallic glasses developed in this work
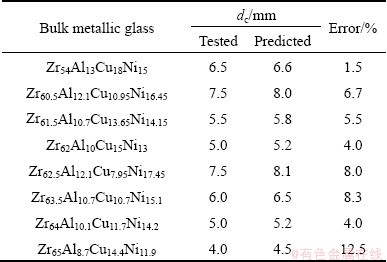
Table 2 Predicted and tested dc values for Cu-Zr-Ti-Ni bulk metallic glasses developed in this work

3 ANN model
Back-propagation artificial neural network (BPANN) and radial basis function artificial neural network RBFANN are thought to be general methods for simulation and prediction modeling. The BPANN has stronger generalization capacity, but it has some shortcomings. It is difficult to determine learning rate, initial weight, objective error, and the numbers of hidden layers and of neurons in hidden layer. Moreover, it would result in the decrease of convergent rate and even be trapped in a local minimum if these parameters can not be suitably and coordinately selected. Nevertheless, the RBFANN has some merits, such as only one adjusted parameter, rapid training procedure and zero error [26-29,35-37]. In addition, the RBFANN is advantageous of the BPANN for better approximating and sorting capacity, and quick learning rate. The base functions among the nodes of the hidden layers for the RBFANN characterize in locality, indicating that the RBFANN is suitable for solving the complex, nonlinear, and local problems. Thus, MATLAB 7.0 package (Neural Network Toolbox from The Math Works Inc.) was used to create the RBFANN model in the present work. The modeling procedures are as follows. Firstly, the data is collected, analyzed and pre-processed. Then the pre-processed data are divided into two kinds of data, i.e., one for training and the other for testing. The third step is to train the neural network. Lastly, the trained neural network is tested.
Sixteen parameters strongly influencing the dc are selected for the inputs of RBFANN model. These parameters are mixing entropy (Smix), difference in atomic radius ratio (Δd), average atomic radius (de), difference in atomic electronegativity ratio (Δe), average atomic electronegativity (ee), Δd /Δe, de/ee, ionicity index (v), fusion heat (ΔHm), fusion temperature (Tm), ΔHm/Tm, specific heat capacity (cp), thermal conductivity (λ), density (ρ), thermal diffusivity (α=λ/ρcp), and thermal storage coefficient (b=(λρcp)1/2). The reasons for the selection and the calculation of these parameters are shown in Refs. [17,18,24,35-37]. In addition, it should be noted that the dc is used to be the output of RBFANN model.
4 Results and discussion
The RBFANN model for predicting and simulating the dc consists of 16 inputs and 1 output. These parameters are calculated by weighted average method with the weight of atomic percentage of each element in metallic glasses [17,18]. Then, these input and output parameters are normalized in the region of (0, 1) to improve the training efficiency according to X=0.1+ 0.8(x-xmin)/(xmax-xmin) (X is the normalization parameter, x is a parameter value, xmin and xmax are the minimum and maximum values for a parameter). The detailed training procedure of the RBFANN is shown in Refs. [35-37]. However, it should be noted that the ratio of the data for training and the datum for testing is confined to be 99:100 during the training and testing procedures. A distribution parameter t was chosen to be 46 because there is the largest linear correlation coefficient (r) between the predicted dc values and the corresponding experimental values. Furthermore, the developed RBFANN model was verified by the data [38-49] in Table 3 in order to examine its efficiency. The relationship between the predicted dc and the experimental value is shown in Fig. 1. As shown in Table 3, the predicted dc values deviate from the corresponding experimental values. However, Fig. 1 presents a better linear relationship and the linear correlation coefficient reaches up to 0.9951, indicating better global performance of the RBFANN model.
In addition, a reliable model should be characterized in not only better global performance but also better local performance including the sorting capacity and the sensitivity to alloying elements. Figure 2 presents the relationships between the predicted dc values and the corresponding experimental values for Zr-based, Fe-based, Mg-based, Ni-based and Cu-based metallic glasses in Table 3.
Table 3 Predicted and tested dc values of metallic glasses [38-49]

Continued
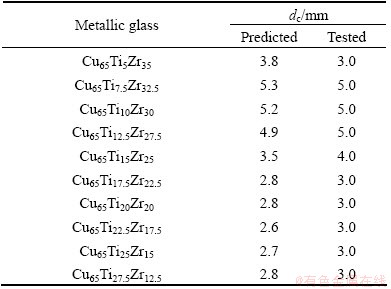

Fig. 1 Relationship between predicted and corresponding tested dc values of metallic glasses in Table 3
It is observed from Fig. 2 that the linear correlation coefficients are 0.9837 for Zr-based metallic glasses, 0.9610 for Fe-based metallic glasses, 0.9887 for Mg-based metallic glasses, 0.9868 for Ni-based metallic glasses, and 0.9344 for Cu-based metallic glasses, respectively. It indicates that the established RBFANN model characterizes in better sorting performance. Of course, there is a difference among the linear correlation coefficients for different alloy systems. It would be due to the different magnitude of samples in the RBFANN model and/or the accuracy of the experimental dc values for different alloy systems.
The sensitivity to large and minor change of the alloying elements is also investigated and presented in Fig. 3. It is clearly seen from Fig. 3 that although the predicted dc values deviate from the corresponding tested values, the change tendency of the predicted dc values to the alloying elements is in good agreement with that of the tested values except for Cu60Ti40-xZrx metallic glasses of 12.5%≤x≤22.5% and 27.5%≤x≤32.5% (Fig. 3(a)) and Zr38Ti17Cu22.5-xBe22.5Cox metallic glasses of 10%≤x≤15% (Fig. 3(b)). Thus, the established RBFANN model is sensitive to the compositional change of the metallic glass.

Fig. 2 Relationships between predicted dc and corresponding dc value for Ni-based (a), Mg-based (b), Fe-based (c), Zr-based (d), and Cu-based (e) metallic glasses, respectively
Furthermore, the dc values of other 218 metallic glasses were predicted whose tested dc values are uncertain, as shown in Fig. 4. Although the values between the predicted dc values and the corresponding tested values are different from each other (not shown here), the linear correlation coefficient is up to 0.9220 (Fig. 4). It indicates better change tendency between the predicted dc values and the tested dc values.
The dc values of Al-based metallic glasses [50-54] with worse GFA were predicted by the established RBFANN model, as shown in Table 4. It is obviously from Table 4 that the predicted and tested dc values of the Al-based metallic glasses are in better agreement with each other. The linear correlation coefficient is up to 0.9347 (Fig. 5(a)), indicating that the predicted and tested dc values of the Al-based metallic glasses are in better agreement with each other in the change tendency. Interestingly, it is found from Fig. 5(b) that the change tendency for the predicted dc of Al85Ni5Y8-xCo2Fex (1≤x≤5) to Fe content is in better agreement with that for the corresponding tested ones. Thus, the established RBFANN model is reliable and adequate.

Fig. 3 Change of predicted and tested dc values of Cu60Ti40-xZrx metallic glasses on Zr (a), Zr38Ti17Cu22.5-xBe22.5Cox metallic glasses on Co (b), (Zr60Al10Cu20Ni10)100-xTix metallic glasses on Ti (c), and Fe77-xNb6B17Yx metallic glasses on Y (d)
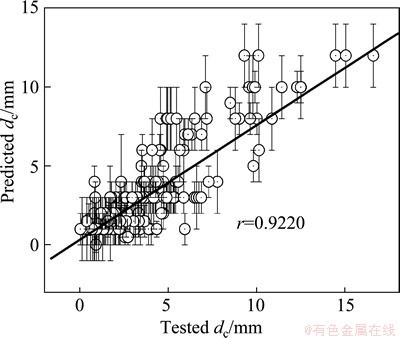
Fig. 4 Relationship between predicted dc and tested values of some metallic glasses
On the other hand, the compositions of a group of Zr-Al-Ni-Cu metallic glasses [12,55-57] were optimized by the established RBFANN model and their dc values were carefully defined by XRD results (not shown herein). The tested and predicted dc values are listed in Table 1. As shown in Table 1, although the error between the tested and the predicted dc values of Zr63.5Al10.7Cu10.7Ni15.1 metallic glass is up to 12.5%, the errors for other Zr-Al-Ni-Cu metallic glasses do not exceed 10%. It indicates that the predicted dc of Zr-Al-Ni-Cu metallic glasses accord with the corresponding tested values. In addition, the relationship between the predicted dc values and the tested values is presented in Fig. 6. It is clearly seen from Fig. 6 that the predicted dc values of Zr-Al-Ni-Cu metallic glasses are in better agreement with the tested ones because the linear correlation coefficient is up to 0.9911.
Table 4 Predicted and tested dc values for Al-based metallic glasses [50-54]
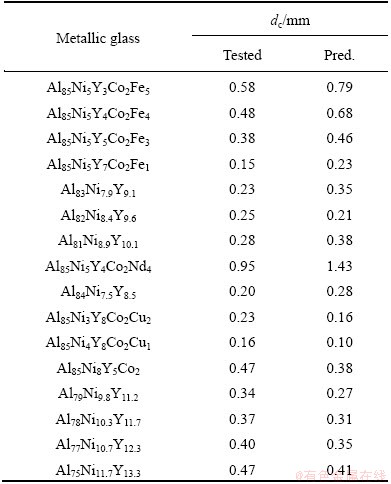

Fig. 5 Relationship between predicted and tested dc values of Al85Ni5Co2Y8-xFex (x=1,3,4,5) metallic glasses listed in Table 4 (a), and change of predicted and tested dc values for Al85Ni5Y8-xCo2Fex metallic glasses on Fe (b)
In order to further examine the reliability of the RBFANN model, Cu-Zr-Ti-Ni glass forming alloys were also designed by the RBFANN. Their compositions are shown in Table 2. Their amorphous structures were ascertained by XRD and their XRD patterns are presented in Fig. 7. The dc values of Cu-Zr-Ti-Ni bulk metallic glasses developed in this work can be determined according to Fig. 7 and are listed in Table 2.
As shown in Table 2, although the dc error of Cu50Zr40Ti10 bulk metallic glass is up to 15.0%, the errors of other Cu-Zr-Ti-Ni bulk metallic glasses do not exceed 10.0%. It indicates that the predicted dc values of Cu-Zr-Ti-Ni bulk metallic glasses are in good agreement with the corresponding tested values. In addition, the relationship between the predicted dc values and the tested values is shown in Fig. 8(a). One can clearly observe from Fig. 8(a) that the linear correlation coefficient is up to 0.9801, indicating that the predicted and tested dc values of Cu-Zr-Ti-Ni bulk metallic glasses agree with each other. Figure 8(b) presents the change of the predicted and tested dc values of Cu-Zr-Ti-Ni bulk metallic glasses to Ni content. It is clearly observed from Fig. 8(b) that the change tendency of the predicted dc values is in good agreement with that of the corresponding tested values. It also indicates that the developed RBFANN model is sensitive to the Ni content in Cu-Zr-Ti-Ni glass forming alloys. In a word, the established RBFANN model can be reliably used to design the composition and predict the dc of glass forming alloy.

Fig. 6 Relationship between predicted dc values and tested dc values of Zr-Al-Ni-Cu bulk metallic glasses developed in this work as shown in Table 1
5 Conclusions
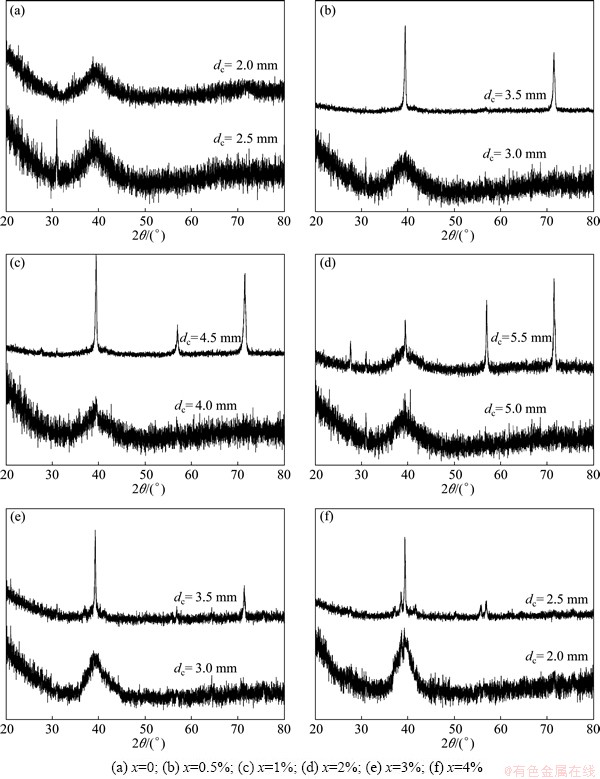
Fig. 7 XRD patterns of Cu50Zr40Ti10-xNix (0≤x≤4%)

Fig. 8 Relationship between predicted dc values and tested dc values (a) and change tendency of predicted and tested dc values to Ni content (b) for Cu-Zr-Ti-Ni bulk metallic glasses developed by us in Table 2
1) The RBFANN model can identify the type of alloys and elements and is sensitive to large and minor change of alloying elements, indicating its global, local, and sorting performance. The predicted results are in good agreement with the corresponding experimental values, indicating that the RBFANN model developed in this work is reliable and adequate for the prediction and the simulation of the critical dimension of glass forming alloys.
2) The predicted dc values of Zr-Al-Ni-Cu and Cu-Zr-Ti-Ni bulk metallic glasses developed in this work are in good agreement with the corresponding experimental values. The change tendency of the predicted dc values is also in good agreement with that of the corresponding tested values. These results indicate that RBFANN model could be reliably used to optimize the compositions and predict the critical dimensions of glass forming alloys.
References
[1] WANG W H, DONG C, SHEK C H. Bulk metallic glasses [J]. Mater Sci Eng R, 2004, 44: 45-89.
[2] WANG W H. Roles of minor additions in formation and properties of bulk metallic glasses [J]. Prog Mater Sci, 2007, 52: 540-596.
[3] INOUE A, ZHANG T. Stabilization of super-cooled liquid and bulk glassy alloys in ferrous and non-ferrous systems [J]. J Non-Cryst Solids, 1999, 250-252: 552-557.
[4] CHEN W, WANG Y, QIANG J, DONG C. Bulk metallic glasses in the Zr-Al-Ni-Cu system [J]. Acta Mater, 2003, 51: 1899-1907.
[5] SCHWARZ R B, HE Y. Formation and properties of bulk amorphous Pd-Ni-P alloys [J]. Mater Sci Forum, 1997, 235: 231-233.
[6] HURBY A. Evaluation of glass-forming tendency by means of DTA [J]. Czech J Phys, 1972, 22: 1187-1193.
[7] LI Y, NG S C, ONG C K, HNG H H, GOH T T. Glass forming ability of bulk glass forming alloys [J]. Scripta Mater, 1997, 36: 783-787.
[8] LU Z P, TAN H, LI Y. The correlation between reduced glass transition temperature and glass forming ability of bulk metallic glasses [J]. Scripta Mater, 2000, 42: 667-673.
[9] LU Z P, LIU C T. A new glass-forming ability criterion for bulk metallic glasses [J]. Acta Mater, 2002, 50: 3501-3512.
[10] XIA L, FANG S S, WANG Q, DONG Y D, LIU C T. Thermodynamic modeling of glass formation in metallic glasses [J]. ApplPhysLett, 2006,88: 171905.
[11] WANG W H. The elastic properties, elastic models and elastic perspectives of metallic glasses [J]. Prog Mater Sci, 2012, 57: 487-656.
[12] CAI A H, XIONG X, LIU Y, AN W K, TAN J Y, PAN Y. Design of new Zr-Al-Ni-Cu bulk metallic glasses [J]. J Alloys Compd, 2009, 468: 432-437.
[13] CAI A H, CHEN H, AN W K, TAN J Y, ZHOU Y. Relationship between melting enthalpy △Hm and critical cooling rate Rc for bulk metallic glasses [J]. Mater Sci Eng A, 2007, 457: 6-12.
[14] CAI A H, PAN Y, GU J, SUN G X. A new criterion for glass forming ability of bulk metallic glasses [J]. Mater Sci Technol, 2006, 22: 859-863.
[15] INOUE A, ZHANG T, MASUMOTO T. Glass-forming ability of alloys [J]. J Non-Cryst Solids, 1993, 156-158: 473-480.
[16] LU Z P, LIU C T. Glass formation criterion for various glass-forming systems [J]. Phys Rev Lett, 2003, 91: 115505.
[17] CAI A H, SUN G X, PAN Y. Evaluation of the parameters related to glass-forming ability of bulk metallic glasses [J]. Mater Des, 2006, 27: 479-488.
[18] CAI A H, PAN Y, SUN G X. New thermodynamic parameter describing glass forming ability of bulk metallic glasses [J]. Mater Sci Technol, 2005, 21: 1222-1226.
[19] CAO H B, MA D, HSIEH K C, DING L, STRATTON W G, VOYLES P M, PAN Y, CAI M D, DICKINSON J T, CHANG Y A. The correlation between reduced glass transition temperature and glass forming ability of bulk metallic glasses [J]. Acta Mater, 2006, 54: 2975-2982.
[20] EGAMI T,WASEDA Y.Atomic size effect on the formability of metallic glasses [J]. JNon-CrystSolids, 1984,64:113-134.
[21] BOTTA W J, PEREIRA F S, BOLFARINI C, KIMINAMI C S, OLIVEIRA M F.Topological instability and electronegativity effects on the glass-forming ability of metallic alloys [J]. Philosophical Magazine Letters, 2008,88:785-791.
[22] MIRACLE D B.Atomic size effect on the formability of metallic glasses [J]. JNon-CrystSolids, 2004,342:89-96.
[23] PANG Chang, JIANG Jian-bing, LUO Ling-jie, GENG Yao-xiang, WANG Ying-min, WANG Qing, DONG Chuang. Ni-Hf metallic glasses and their atomic cluster formulas [J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2012, 42(5): 592-597. (in Chinese)
[24] GUO S, LIU Y. Estimation of critical cooling rates for formation of amorphous alloys from critical sizes [J]. J Non-Cryst Solids, 2012, 358: 2753-2758.
[25] CAI A H, XIONG X, LIU Y, AN W K, ZHOU G J, LUO Y, LI T L, LI X S. Estimation of glass forming ability of Mg-based alloys based on thermodynamics [J]. J Non-Cryst Solids, 2013, 376: 68-75.
[26] AN W K, CAI A H, LUO Y, CHEN H, LIU W X, LI T L, CHEN M. Optimization of composition of as-cast chromium white cast iron based on wear-resistant performance [J]. Mater Des, 2009, 30: 2339-2344.
[27] CAI A H, CHEN H, AN W K, LI X S, ZHOU Y. Optimization of composition and technology for phosphate graphite mold [J]. Mater Des, 2008, 29: 1835-1839.
[28] CAI A H, ZHOU Y, TAN J Y, LUO Y, LI T L, CHEN M, AN W K. Optimization of composition of heat-treated chromium white cast iron casting by phosphate graphite mold [J]. J Alloys Compd, 2008, 466: 273-280.
[29] CAI A H, CHEN H, AN W K, LIU W X, LUO Y, LI T L, CHEN M. Robust optimisation of chemical composition of as cast chromium white cast iron using a green sand mould [J]. Mater Sci Technol, 2008, 24: 302-308.
[30] YANG Xia-wei, ZHU Jing-chuan, NONG Zhi-sheng, HE Dong, LAI Zhong-hong, LIU Ying, LIU Fa-wei. Prediction of mechanical properties of A357 alloy using artificial neural network [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 788-795.
[31] YANG Xia-wei, ZHU Jing-chuan, HE Dong, LAI Zhong-hong, NONG Zhi-sheng, LIU Yong. Optimum design of flow distribution in quenching tank for heat treatment of A357 aluminum alloy large complicated thin-wall workpieces by CFD simulation and ANN approach [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 1442-1451.
[32] LIN Yi, ZHENG Zi-qiao, ZHANG Hai-feng, HAN Ye. Effect of heat treatment process on tensile properties of 2A97 Al-Li alloy: Experiment and BP neural network simulation [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 1728-1736.
[33] SENTHILKUMAR V, BALAJI A, ARULKIRUBAKARAN D. Application of constitutive and neural network models for prediction of high temperature flow behavior of Al/Mg based nanocomposite [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 1737-1750.
[34] KEONG K G, SHA W, MALINOV S. Artificial neural network modelling of crystallization temperatures of the Ni-P based amorphous alloys [J]. Mater Sci Eng A, 2004, 365: 212-218.
[35] CAI A H, XIONG X, LIU Y, AN W K, TAN J Y. Artificial neural network modeling of reduced glass transition temperature of glass forming alloys [J]. Appl Phys Lett, 2008, 92: 111909.
[36] CAI A H, XIONG X, LIU Y, AN W K, TAN J Y, LUO Y. Artificial neural network modeling for undercooled liquid region of glass forming alloys [J]. Compt Mater Sci, 2010, 48: 109-114.
[37] CAI A H, LIU Y, AN W K, ZHOU G J, LUO Y, LI T L, LI X S, TAN X F. Prediction of critical cooling rate for glass forming alloys by artifi cial neural network [J]. Mater Des, 2013, 52: 671-676.
[38] XING Da-wei, SHEN Jun, SUN Jian-fui, WANG Gang, YAN Ming. Glass forming ability of bulk (Zr0.6Cu0.2Ni0.1Al0.1)100-xTix amorphous alloys [J]. Journal of Harbin Institute of Technology, 2004, 36(9): 1265-1268. (in Chinese)
[39] WU Xiao-feng, ZHANG Hai-feng, QIU Ke-qiang, YANG Hong-cai, HU Zhuang-qi. Preparation and mechanical properties of Zr-based containing Co bulk metallic glass [J]. Rare Metal Materials and Engineering, 2004, 33(12): 1317-1320. (in Chinese)
[40] ZHANG Tao, MEN Hua, TI Yun-jie. Formation and mechanical properties of Cu-Ti-Zr bulk glassy alloys [J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(10): 925-929.
[41] SONG D S, KIM J H, FLEURY E, KIM W T, KIM D H. Synthesis of ferromagnetic Fe-based bulk glassy alloys in the Fe-Nb-B-Y system [J]. J Alloys Compd, 2005, 389: 159-164.
[42] XU D H, DUAN G, JOHNSON W L, GARLAND C. Formation and properties of new Ni-based amorphous alloys with critical casting thickness up to 5 mm [J]. Acta Mater, 2004, 52: 3493-3497.
[43] WANG L M, LI C F, INOUE A. Formation and mechanical properties of bulk glassy Ni57-xTi23Zr15Si5Pdx alloys [J]. Trans JIM, 2001, 42: 886-889.
[44] LEE J Y, BAE D H, LEE J K, KIM D H. Bulk glass formation in the Ni-Zr-Ti-Nb-Si-Sn alloy system [J]. J Mater Res, 2004, 19: 2221-2225.
[45] XING L Q, ECKERT J,  W, SCHULTZ L. High strength materials produced by precipitation of icosahedral quasicrystals in bulk Zr-Ti-Ni-Cu-Al amorphous alloys [J]. Appl Phys Lett, 1999, 74: 664-666.
W, SCHULTZ L. High strength materials produced by precipitation of icosahedral quasicrystals in bulk Zr-Ti-Ni-Cu-Al amorphous alloys [J]. Appl Phys Lett, 1999, 74: 664-666.
[46] MATTERN N, ECKERT J,  U. Structural behavior of Zr52Ti5Cu18Ni15Al10 bulk metallic glass at high temperatures [J]. Appl Phys Lett, 2002, 80: 4525-4527.
U. Structural behavior of Zr52Ti5Cu18Ni15Al10 bulk metallic glass at high temperatures [J]. Appl Phys Lett, 2002, 80: 4525-4527.
[47] WANLUK T A, SCHROERS J, JOHNSON W L. Critical cooling rate and thermal stability of Zr-Ti-Ni-Cu-Be alloys [J]. Appl Phys Lett, 2001, 78: 1213-1215.
[48] YI S, LEE J K, KIM W T, KIM D H. Ni-based bulk amorphous in the Ni-Ti-Zr-Si system [J]. J Non-Cryst Solids, 2001, 291: 132-136.
[49] YUAN G Y, INOUE A. The effect of Ni substitution on the glass-forming ability and mechanical properties of Mg-Cu-Gd metallic glass alloys [J]. J Alloys Compd, 2005, 387: 134-138.
[50] LOUZGUINE D V, INOUE A. Investigation of structure and properties of the Al-Y-Ni-Co-Cu metallic glasses [J]. J Mater Res, 2002, 17: 1014-1018.
[51]  HEUNEN G, VARGA L K,
HEUNEN G, VARGA L K,  S. Real time synchrotron studies on amorphous Al85Ce5Ni8Co2 and Al85Y5Ni8Co2 alloys [J]. J Alloys Compd, 2004, 368: 164-168.
S. Real time synchrotron studies on amorphous Al85Ce5Ni8Co2 and Al85Y5Ni8Co2 alloys [J]. J Alloys Compd, 2004, 368: 164-168.
[52] BASSIM N, KIMINAMI C S, KAUFMAN M J, OLIVEIRA M F. Crystallization behavior of amorphous Al84Y9Ni5Co2 alloy [J]. Mater Sci Eng A, 2001, 304-306: 332-337.
[53] FREITAG J M, KOKNAEV R G, SABET-SHARGHI R, KOKNAEVA M. Mechanical properties of Al-Y-Ni amorphous ribbons [J]. J Appl Phys, 1996, 78: 3967-3970.
[54] LOUZGUINE D V, INOUE A. Strong influence of supercooled liquid on crystallization of the Al85Ni5Y4Nd4Co2 metallic glass [J]. Appl Phys Lett, 2001, 78: 3061-3063.
[55] CAI A H, XIONG X, LIU Y, LI J H, AN W K, LUO Y. Characteristics of near-eutectic and off-eutectic Zr-Al-Ni-Cu glass forming alloys [J]. Mater Sci Eng A, 2009, 516: 100-102.
[56] AN W K, XIONG X, LIU Y, LI J H, CAI A H, LUO Y, LI T L, LI X S. Investigation of glass forming ability and crystallization kinetics of Zr63.5Al10.7Cu10.7Ni15.1 bulk metallic glass [J]. J Alloys Compd, 2009, 486: 288-292.
[57] CAI A H, AN W K, LUO Y, LI T L, LI X S, XIONG X, LIU Y. Glass forming ability, non-isothermal crystallization kinetics, and mechanical property of Zr61.5Al10.7Cu13.65Ni14.15 metallic glass [J]. J Alloys Compd, 2010, 490: 642-646.
基于临界尺寸采用人工神经网络技术优化设计玻璃形成合金的成分
蔡安辉1,2,熊 翔2,刘 咏2,安伟科1,周果君1,罗 云1,李铁林1,李小松1,谭湘夫1
1. 湖南理工学院 机械工程学院,岳阳 414006;
2. 中南大学 粉末冶金国家重点实验室,长沙 410083
摘 要:建立一个用于预测和模拟玻璃形成合金的临界尺寸的人工神经网络模型;基于该人工神经网络模型优化设计一系列Zr-Al-Ni-Cu和Cu-Zr-Ti-Ni块体非晶合金的成分并对其临界尺寸进行预测。采用真空喷注法制备Zr-Al-Ni-Cu和Cu-Zr-Ti-Ni块体非晶合金试样。这些块体合金的非晶态结构采用X射线衍射法进行表征并确定这些合金的非晶形成的临界尺寸。结果表明,预测的临界尺寸与实验结果吻合较好,所建立的神经网络模型能可靠地设计非晶合金的成分和预测非晶合金的临界尺寸。
关键词:临界尺寸;玻璃形成合金;人工神经网络;非晶
(Edited by Hua YANG)
Foundation item: Project (50874045) supported by the National Natural Science Foundation of China
Corresponding author: An-hui CAI; Tel: +86-730-8648848; E-mail: cah1970@sohu.com
DOI: 10.1016/S1003-6326(14)63213-1
Abstract: An artificial neural network (ANN) model was developed for simulating and predicting critical dimension dc of glass forming alloys. A group of Zr-Al-Ni-Cu and Cu-Zr-Ti-Ni bulk metallic glasses were designed based on the dc and their dc values were predicted by the ANN model. Zr-Al-Ni-Cu and Cu-Zr-Ti-Ni bulk metallic glasses were prepared by injecting into copper mold. The amorphous structures and the determination of the dc of as-cast alloys were ascertained using X-ray diffraction. The results show that the predicted dc values of glass forming alloys are in agreement with the corresponding experimental values. Thus the developed ANN model is reliable and adequate for designing the composition and predicting the dc of glass forming alloy.


