
J. Cent. South Univ. (2021) 28: 848-865
DOI: https://doi.org/10.1007/s11771-021-4649-2

Experimental study on energy storage and dissipation characteristics of granite under two-dimensional compression with constant confining pressure
SU You-qiang(速佑强)1, GONG Feng-qiang(宫凤强)1, 2, LUO Song(罗松)1, LIU Zhi-xiang(刘志祥)1
1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
2. School of Civil Engineering, Southeast University, Nanjing 211189, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract:
To study the energy storage and dissipation characteristics of deep rock under two-dimensional compression with constant confining pressure, the single cyclic loading-unloading two-dimensional compression tests were performed on granite specimens with two height-to-width (H/W) ratios under five confining pressures. Three energy density parameters (input energy density, elastic energy density and dissipated energy density) in the axial and lateral directions of granite specimens under different confining pressures were calculated using the area integral method. The experimental results show that, for the specimens with a specific H/W ratio, these three energy density parameters in the axial and lateral directions increase nonlinearly with the confining pressure as quadratic polynomial functions. Under constant confining pressure compression, the linear energy storage law of granite specimens in the axial and lateral directions was founded. Using the linear energy storage law in different directions, the elastic energy density in various directions (axial elastic energy density, lateral elastic energy density and total elastic energy density) of granite under any specific confining pressures can be calculated. When the H/W ratio varies from 1:1 to 2:1, the lateral compression energy storage coefficient increases and the corresponding axial compression energy storage coefficient decreases, while the total compression energy storage coefficient is almost independent of the H/W ratio.
Key words:
Cite this article as:
SU You-qiang, GONG Feng-qiang, LUO Song, LIU Zhi-xiang. Experimental study on energy storage and dissipation characteristics of granite under two-dimensional compression with constant confining pressure [J]. Journal of Central South University, 2021, 28(3): 848-865.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-021-4649-21 Introduction
More and more adjacent tunnels and mines have been widely employed in deep rock projects [1], and the surrounding rock masses at sidewall and bord are under a two-dimensional high stress state (σ1≥σ2≥σ3=0) after excavation unloading [2, 3]. Two-dimensional compression test and numerical simulation test under constant confining pressure are often used to simulate the stress state of deep rock mass, and many scientific and practical discoveries and conclusions have been obtained [2-8].
It is generally known that, the deformation and failure of rock are driven by energy conversion, including energy input, storage, dissipation, and release [9-13]. The existing theoretical and laboratory studies also confirmed that energy plays an important role in evaluating the mechanical properties of rocks [14-19]. Based on uniaxial compression tests, XIE et al [9] demonstrated that the strain energy released from rock plays a key role in rock structure mutation failure. LI et al [20] illustrated that the absorbed strain energy, damage strain energy, and elastic energy increase with an increase in strain rate. HOU et al [21] revealed the effect of bedding orientation on the mechanical property and energy evolution characteristics of shales. MUNOZ et al [22] proposed a new energy-based brittleness index that successfully describes the performance of different cutting and drilling methods. Moreover, according to uniaxial cyclic loading-unloading tests, MENG et al [23] revealed the characteristic of acoustic emission and energy evolution of red sandstone. GONG et al [18, 24-26] found the linear energy storage and dissipation laws existed in uniaxial compression test for various rocks, and these laws were used to establish the rock burst proneness indices of rock materials. Furthermore, via the two-dimensional compression test, LI et al [27] obtained that the total energy absorbed, the stored releasable strain energy, and the energy dissipation before rock failure increase with the increasing lateral pressure. WANG et al [28] found that elastic strain energy limit, the ratio of elastic strain energy to total energy absorbed and the ratio of dissipation energy to the total energy for coal rock are all a constant. YANG et al [29] suggested that the energy absorption capacity decreases as the biaxial compression stress ratio increases.
Most of the existing studies focused on the evolution characteristics of input energy density (IED), elastic energy density (EED), and dissipated energy density (DED) with loading stress and strain, and the linear energy storage and dissipation laws were confirmed in the uniaxial compression tests. However, under two-dimensional stress conditions, the relationships between IED, EED, and DED of rocks have not been investigated yet. Hence, it is necessary to conduct simulated the test in a laboratory scale to study the energy storage and dissipation characteristics of rocks under two- dimensional geo-stress conditions.
In the present study, we conducted a series of single cyclic loading-unloading two-dimensional compression (SCLUTDC) tests to investigate the energy storage and dissipation characteristics, and the height-to-width (H/W) ratio effect was also considered. The evolution characteristics of three energy density parameters (EED, DED and IED) of granite in the axial and lateral directions were also investigated. Moreover, the relationships between the total input energy density (TIED), total elastic energy density (TEED) and total dissipated energy density (TDED) of granite specimens with two H/W ratios were further analyzed and discussed.
2 Experimental
2.1 Specimen preparation and test equipment
In this experiment, the granite specimens were collected from Yueyang City, Hunan Province of China. The specimens were processed into two H/W ratios with dimensions of 50 mm×50 mm×50 mm (H/W=1:1) and 50 mm×50 mm×100 mm (H/W= 2:1), and the six surfaces of each specimen were polished with a sander. The machining accuracy was in strict accordance with the standard of International Society for Rock Mechanics [30]. The granite specimens with 1:1 H/W ratio were named as U-X and B-X, such as U-1 and B-1; the granite specimens with 2:1 H/W ratio were named as G-U-X and G-B-X, such as G-U-1 and G-B-1. The basic physical parameters of the specimens are summarized in Table 1. The specimens numbered G-U-1 and U-1 were used for uniaxial compression (UC) tests, and the remaining specimens were used for the SCLUTDC tests.
The schematic diagrams of the granite specimens with two height-to-width ratios under two-dimensional compression are shown in Figures 1(a) and (b). The tests on the rock specimens with two H/W ratios were carried out on a two-dimensional loading testing system, which comprises an independent axial loading device, a lateral loading device, and a data acquisition component. The axial and lateral maximum loading loads are 2000 and 250 kN, respectively. The axial deformation was measured using an extensometer with a range of 10 mm; the lateral deformation was obtained by an extensometer with a range of 10 mm.
2.2 Testing schemes
The UC and SCLUTDC tests were performed. First, the uniaxial compressive strength (UCS) values (σc) of rock specimens with two H/W ratios were obtained by the UC test with a load rate of 1 MPa/s. Subsequently, a series of SCLUTDC tests were carried out under a constant confining pressure. In the SCLUTDC tests, the same loading path and loading rate were used for the specimens with two H/W ratios. Therefore, taking the loading path of granite specimens with 1:1 H/W ratio in SCLUTDC tests as an example, we elaborated on it as follows (Figure 1(c)):
Both the axial stress (σ1) and confining pressure (σ2) of the granite specimens with 1:1 H/W ratio are simultaneously loaded to a predetermined confining pressure (5, 10, 15, 20 or 25 MPa) with a loading rate of 150 kN/min (1 MPa/s), and then simultaneously unloaded at the same rate (1 MPa/s) until the axial stress and confining pressure are zero.
Table 1 Basic physical parameters of granite specimens with two H/W ratios
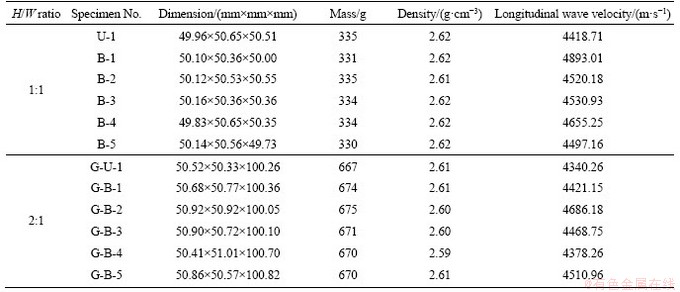
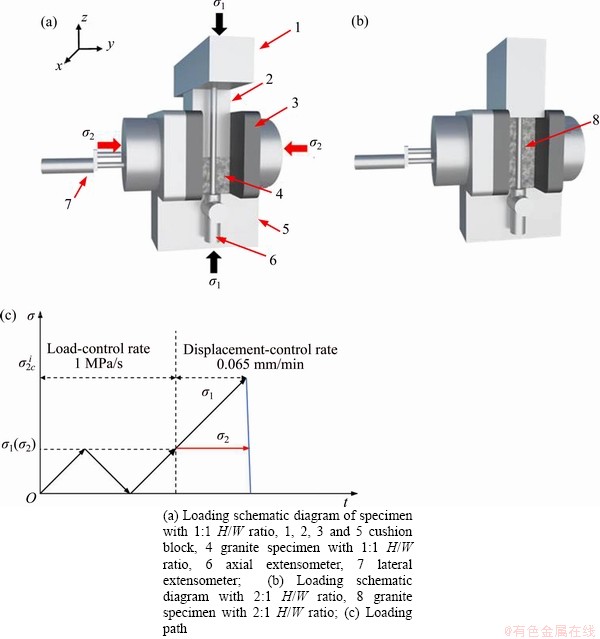
Figure 1 SCLUTDC of granite specimens:
The axial stress and confining pressure are simultaneously reloaded to a predetermined confining pressure (5, 10, 15, 20 or 25 MPa) with a loading rate of 150 kN/min (1 MPa/s), then the confining pressure was kept unchanged and the axial stress continued to increase with a rate of 0.065 mm/min until specimen failure.
2.3 Calculation method for energy density parameters
The deformation and failure of rock under two-dimensional constant confining pressure compression can be regarded as a closed system without thermal energy conversion. The total input energy density Ui at a fixed confining pressure i can be obtained by summing the corresponding axial input energy density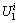 (AIED) and the lateral input energy density
(AIED) and the lateral input energy density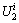 (LIED). Additionally, the total input energy density can also be obtained by summing the total elastic energy density
(LIED). Additionally, the total input energy density can also be obtained by summing the total elastic energy density and the total dissipated energy density
and the total dissipated energy density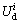 at a determined confining pressure i [13]. Hence, the total input energy density can be calculated by Eq. (1).
at a determined confining pressure i [13]. Hence, the total input energy density can be calculated by Eq. (1).
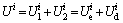 (1)
(1)
where and
and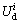 of the specimens at a confining pressure i can be expressed by Eq. (2).
of the specimens at a confining pressure i can be expressed by Eq. (2).
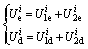 (2)
(2)
where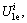
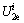 and
and 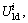
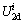 are the elastic energy densities (EED) and dissipated energy densities (DED) in axial and lateral directions, respectively.
are the elastic energy densities (EED) and dissipated energy densities (DED) in axial and lateral directions, respectively.
The IED (U), EED (Ue) and DED (Ud) in axial and lateral directions at the corresponding confining pressure i can be separately calculated using Eqs. (3) and (4) as follows (also see Figure 2):
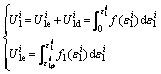 (3)
(3)
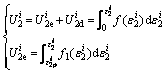 (4)
(4)
where is the axial elastic energy density (AEED),
is the axial elastic energy density (AEED), is the axial dissipated energy density (ADED) corresponding to axial stress (σ1), respectively,
is the axial dissipated energy density (ADED) corresponding to axial stress (σ1), respectively, and
and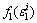 are the axial loading curvilinear function and the axial unloading
are the axial loading curvilinear function and the axial unloading
curvilinear function, respectively.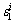 and
and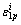 are the axial total strain value and the permanent axial strain on the axial stress-axial strain curve, respectively;
are the axial total strain value and the permanent axial strain on the axial stress-axial strain curve, respectively;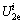 and
and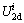 are the lateral elastic energy density (LEED) and the lateral dissipated energy density (LDED) corresponding to confining pressure (σ2), respectively.
are the lateral elastic energy density (LEED) and the lateral dissipated energy density (LDED) corresponding to confining pressure (σ2), respectively.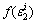 and
and are the lateral loading curvilinear function and the lateral unloading curvilinear function,respectively.
are the lateral loading curvilinear function and the lateral unloading curvilinear function,respectively.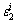 and
and 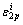 are the lateral total strain value and the permanent lateral strain value on the lateral stress-lateral strain curve, respectively. The AIED (LIED) is the area enclosed by the initial loading curve and the abscissa axis. The AEED (LEED) is the area enclosed by the unloading curve and abscissa axis. Hence, the ADED (LDED) is equal to the difference between the AIED (LIED) and the corresponding AEED (LEED) at the corresponding confining pressure i.
are the lateral total strain value and the permanent lateral strain value on the lateral stress-lateral strain curve, respectively. The AIED (LIED) is the area enclosed by the initial loading curve and the abscissa axis. The AEED (LEED) is the area enclosed by the unloading curve and abscissa axis. Hence, the ADED (LDED) is equal to the difference between the AIED (LIED) and the corresponding AEED (LEED) at the corresponding confining pressure i.
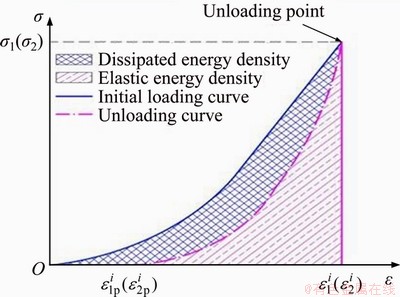
Figure 2 Calculation method of energy density parameters in axial and lateral directions under SCLUTDC
3 Stress-strain curves and failure characteristics
In the tests, the deformations of cushion block and specimen were measured at the same time during the loading process. Then the deformation of the cushion block was deducted before the stress-strain curve was drawn. The axial stress-axial strain curves of granite specimens with two H/W ratios (1:1 and 2:1) in the UC tests are shown in Figure 3. The UCS values of the specimens with H/W ratios of 1:1 and 2:1 are 183.74 and 156.51 MPa, respectively. It was observed that the UCS of specimen with 1:1 H/W ratio is higher, and that the post-peak part of the axial stress-axial strain curve becomes steeper when the H/W ratio increases [31]. Figure 4 shows the typical axial and lateral stress-strain curves of the specimens with two H/W ratios in the SCLUTDC tests. It can be clearly differentiated that the pre-peak axial stress-axial strain curve of the specimen with 1:1 H/W ratio is smooth under the confining pressure of 20 MPa, while that of the specimen with 2:1 H/W ratio has a turning point when the axial stress is close to 5 MPa. Meanwhile, the post-peak axial stress-axial strain curve is steeper with a greater H/W ratio of the specimen. The lateral stress-lateral strain curves of specimens with two H/W ratios are generally consistent, and lateral stress finally tends to the confining pressure. The axial and lateral loading-unloading stress- strain curves of the granite specimens with two H/W ratios in SCLUTDC tests are given in Figures 5 and 6. These figures clearly show that unloading curves are lower than the loading curves as a consequence of the energy dissipation during the initial loading process.
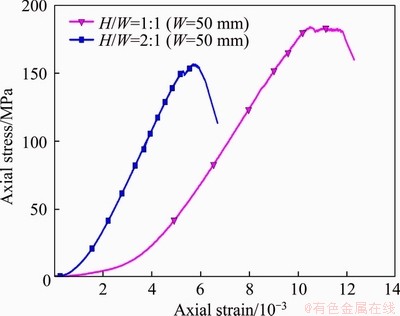
Figure 3 Axial stress-axial strain curves of granite specimens with two H/W ratios in UC tests
Figure 7 shows the peak compressive strength of the specimens with two H/W ratios under different confining pressures. As noted in Figure 7, the peak compressive strength decreases with increasing the H/W ratio under a constant confining pressure, and it also basically increases with the confining pressure for the specimens with the same H/W ratio. Moreover, the peak compressive strengths of the specimens with 1:1 H/W ratio under 0 and 5 MPa confining pressures are 183.7 and 167.9 MPa, respectively, which is obviously not consistent with the theory. The reason of the above phenomenon is the difference of stress path. When the confining pressure changes from 0 to 5 MPa, the stress state of the specimen changes from one dimension to two dimensions. With the confining pressure increased, the peak compressive strength of specimen with the same H/W ratio also increased. However, the peak compressive strength under 5 MPa confining pressure is lower than that under 0 MPa confining pressure, which is consistent with the results reported by AMADEI and ROBINSON [32].

Figure 4 Representative stress-strain curves of granite specimens with two H/W ratios in SCLUTDC tests:
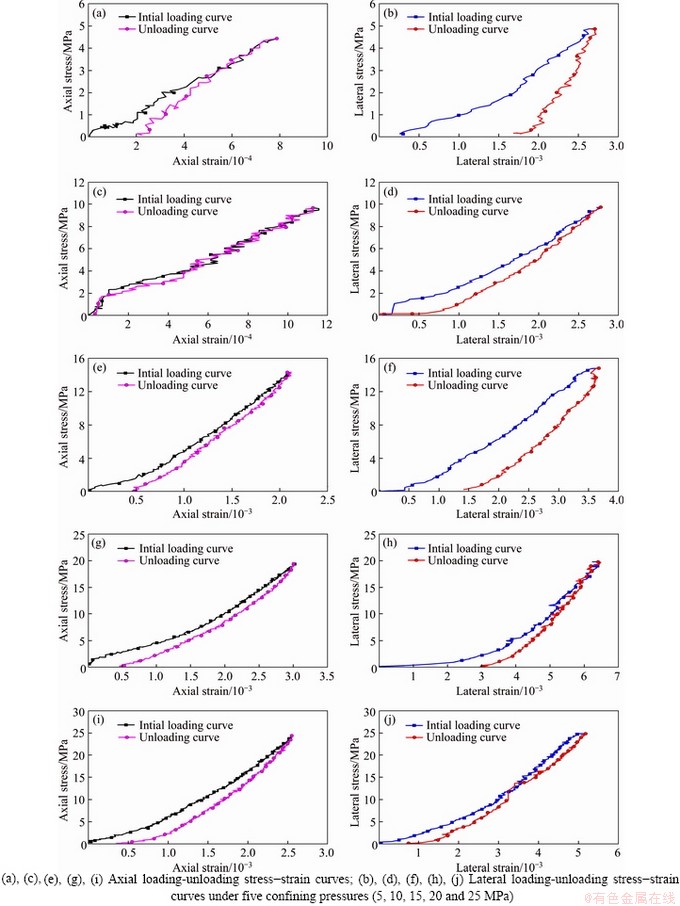
Figure 5 Loading-unloading stress-strain curves of granite specimens with 1:1 H/W ratio in SCLUTDC tests:
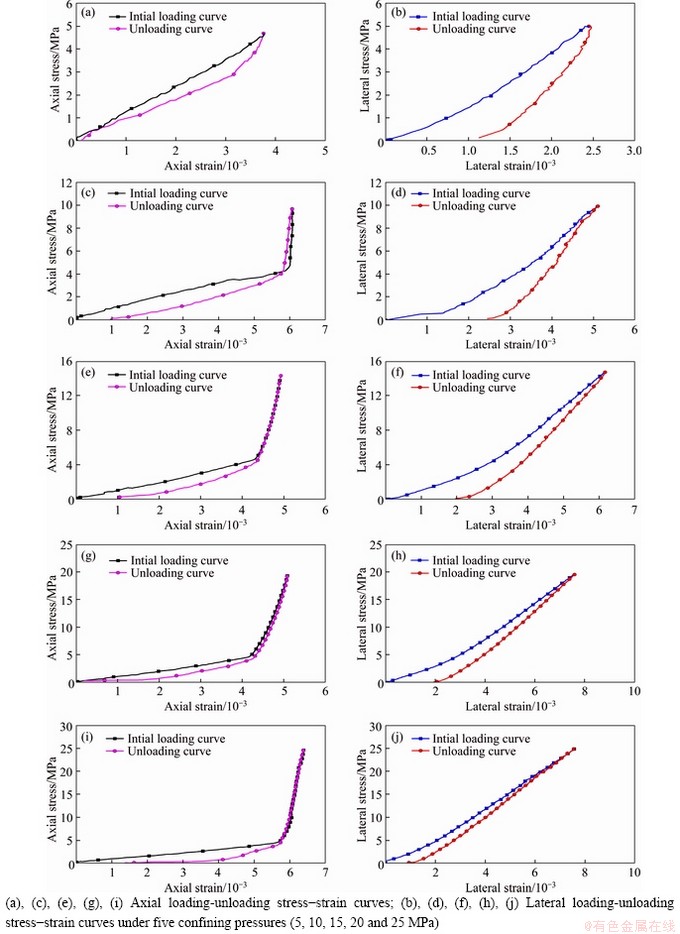
Figure 6 Loading-unloading stress-strain curves of granite specimens with 2:1 H/W ratio in the SCLUTDC tests:
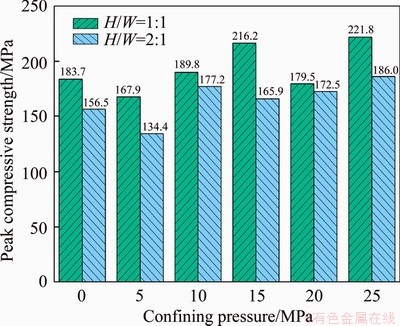
Figure 7 Peak compressive strength of specimens with two H/W ratios under different confining pressures
Figure 8 shows the fragmental states of specimens U-1 and G-U-1 in the UC tests, and Figure 9 shows the fragments of specimens B-5 and G-B-5 following failure in the SCLUTDC tests. Rock fragments ejected during the specimen failure in the UC and SCLUTDC tests. Compared with the UC tests, less rock fragments were ejected in the SCLUTDC tests. This observation was attributed to the reduction in the free surface of the specimens subjected to a two-dimensional compression where the specimens suffered from a confining pressure restraint. From Figures 9(a) and (b), it was observed that the specimens with two H/W ratios failed in shear mode.
4 Test results
4.1 Relationships between energy density parameters and confining pressure
According to the axial and lateral loading- unloading stress-strain curves of the specimens in the SCLUTDC tests, the IED, EED, and DED in axial and lateral directions under different confining pressures can be calculated using Eqs. (3) and (4). The TIED, TEED, and TDED can be obtained by the summation of the axial and lateral energy density parameters.
The variations in IED, EED, and DED of the granite specimens tested under various confining pressure are illustrated in Figures 10 and 11 (In these figures, the coordinate point (0, 0) is used to correct the deviation). It turns out that the IED, EED, and DED in axial and lateral directions of granite specimens with two H/W ratios increase nonlinearly with the confining pressure as quadratic polynomial functions, so are the TIED, TEED and TDED. The quadratic polynomial functions and correlation coefficients (R2) are listed in Tables 2 and 3. Compared with three axial energy density parameters (AIED, AEED and ADED) of the pecimens with 2:1 H/W ratio, those of the specimens with 1:1 H/W ratio increase rapidly with an increase in confining pressure, whereas the changes in the three lateral energy density parameters (LIED, LEED and LDED) of the specimens with two H/W ratios under various confining pressures are generally consistency.

Figure 8 Representative failure mode of specimens with two H/W ratios in UC tests:

Figure 9 Representative failure mode of specimens with two H/W ratios in SCLUTDC tests under two-dimensional compression:
For the specimens with two H/W ratios, the changes in the three total energy density parameters versus the confining pressure are roughly consistent. The EED curves are considerably similar to the corresponding IED curve, whereas the corresponding DED curve deviates farther from them.
4.2 Relationships between EED, DED and IED in axial and lateral directions
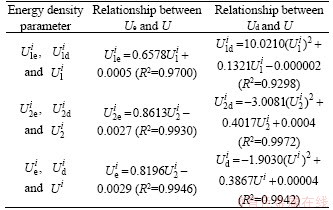
To further investigate the relationships among the EED, DED, and IED of granite specimens with two H/W ratios under different confining pressures, the corresponding data were fitted, as shown in Figures 12 and 13.Whether the H/W ratio is 1:1 or 2:1, the EEDs in axial and lateral directions increase linearly with increasing the corresponding IED, so is the TEED with the TIED. The fact that the linear correlation coefficients are greater than 0.9690 indicates that the EEDs in various directions of the specimens with two H/W ratios have a strong correlation with the corresponding IED. This finding confirmed the linear energy storage law of the granite under two-dimensional constant confining pressure compression. Moreover, the DEDs in axial and lateral directions increase nonlinearly with an increase in the corresponding IED as quadratic polynomial functions, so is the TDED with the TIED. The fitting functions and R2 of the granite specimens with two H/W ratios between EED, DED, and IED are summarized in Tables 4 and 5.
4.3 Compression energy storage coefficients
To clearly describe the energy storage performance of granite under two-dimensional stress conditions, the concepts of compression energy storage coefficient (CESC) was proposed based on the linear storage law in various directions, which includes the axial compression energy storage coefficient (ACESC), the lateral compression energy storage coefficient (LCESC), and the total compression energy storage coefficient (TCESC). The CESCs can be expressed as the ratio of the EED to the corresponding IED in the linear fitting functions. The constant terms in the fitting expressions can be ignored because they are 1-3 orders of magnitude lower than the corresponding CESCs. The CESCs can be defined as follows:
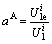 (5)
(5)
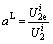 (6)
(6)
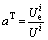 (7)
(7)
where aA is the axial compression energy storage coefficient (ACESC); aL is the lateral compression energy storage coefficient (LCESC); aT is the total compression energy storage coefficient (TCESC).
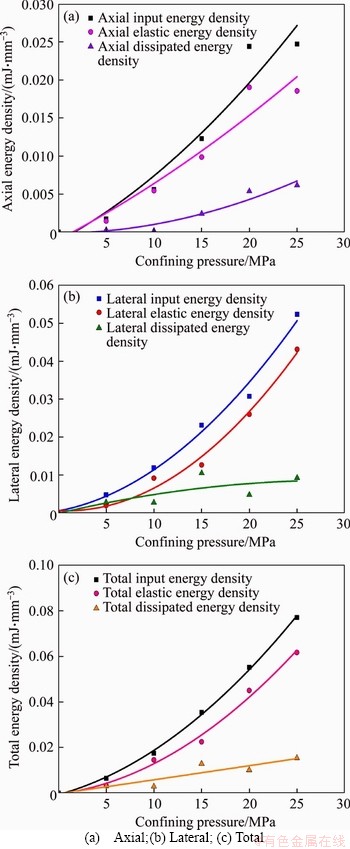
Figure 10 Change laws of IED, EED and DED in various directions of granite specimens with 1:1 H/W ratio under five confining pressures:
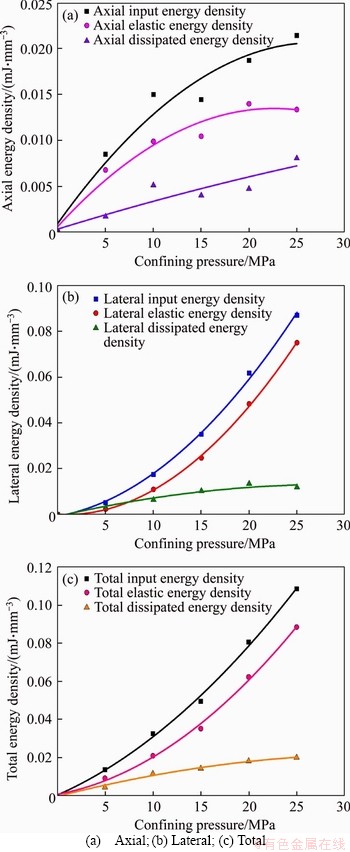
Figure 11 Change laws of IED, EED and DED in various directions of granite specimens with 2:1 H/W ratio under five confining pressures:
Table 2 Fitting functions between IED, EED, DED of granite specimen with 1:1 H/W ratio and the confining pressure

Table 3 Fitting functions between the IED, EED, DED of the granite specimen with 2:1 H/W ratio and confining pressure

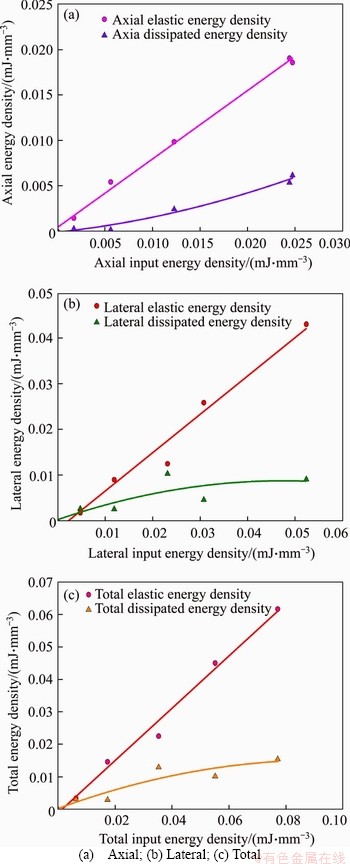
Figure 12 Relationships between EED, DED and IED of granite specimen with 1:1 H/W ratio:
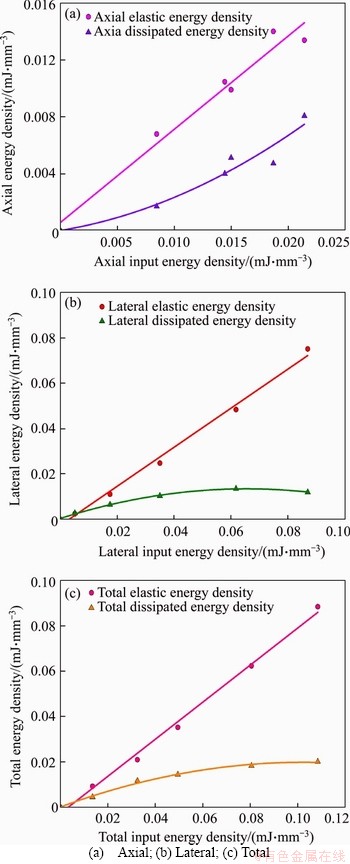
Figure 13 Relationships between EED, DED and IED of granite specimen with 2:1 H/W ratio:
Table 4 Fitting functions between EED, DED, and IED of granite specimen with 1:1 H/W ratio
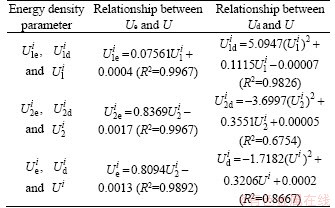
Table 5 Fitting functions between EED, DED, and IED of the granite specimen with 2:1 H/W ratio
For the granite specimens with H/W ratios of 1:1 and 2:1, the ACESCs are 0.7561 and 0.6578, LCESCs are 0.8369 and 0.8613, and TCESCs are 0.8094 and 0.8196, respectively. The CESC represents the energy storage capacity of specimens in the tests. It can be observed that the LCESCs of the granite specimens are greater than the related ACESCs, indicating that the lateral energy storage dominates in the SCLUTDC tests. When the H/W ratio varies from 1:1 to 2:1, the LCESC increases and the ACESC decreases, while the corresponding TCESC is almost independent of the specimen H/W ratio. In the UC tests, LIANG et al [33] found that the IED, EED, and DED decrease with increasing the length/diameter ratio of granite specimens. In this study, the total energy storage coefficient was introduced to characterize the potential of granite for storing energy, and the total energy storage coefficient was equal to the ratio of the EED to IED. The energy storage coefficients of the specimens with 1:1 and 2:1 H/W ratios in our study were 0.8094 and 0.8196, respectively. The H/W ratio only changes the axial and lateral CESCs, and it does not affect the total energy storage law of the granite specimen. The above results further illustrate that, in the SCLUTDC tests, the total energy storage coefficient of rock is constant, which is a material parameter of rock material itself.
4.4 Application of linear energy storage law
According to the linear energy storage law described herein before, the EED or DED of rock specimens under any specific confining pressures can be calculated: using 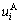 obtained from the axial stress-axial strain curves,
obtained from the axial stress-axial strain curves,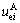 and
and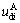 can be calculated via Eq. (8);
can be calculated via Eq. (8);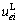 and
and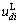 can be calculated in terms of the Eq. (9) and
can be calculated in terms of the Eq. (9) and  obtained from the lateral stress-lateral strain curves; when
obtained from the lateral stress-lateral strain curves; when 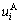 and
and  were acquired, the corresponding
were acquired, the corresponding 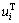 can also be calculated by Eq. (2) in Section 2.3, and thereby
can also be calculated by Eq. (2) in Section 2.3, and thereby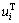 can be substituted into Eq. (10) to attain
can be substituted into Eq. (10) to attain 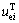 and
and 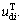
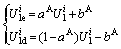 (8)
(8)
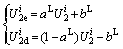 (9)
(9)
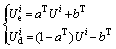 (10)
(10)
where aA, aL and aT are the ACESC, LCESC, TCESC, respectively; bA, bL and bT are three constant terms in the linear fitting functions.
Applying the linear energy storage law of the specimens in various directions, the evolution process of the EED and DED can be obtained. Figures 14 and 15 show the energy evolution trend of three energy density parameters with two H/W ratios under the same confining pressure i (i=25 MPa). For the specimens with a specific H/W ratio, the IED, EED and DED in axial and lateral directions increase nonlinearly with the axial strain, so are the TIED, TEED and TDED.
5 Discussion
Figure 4 in Section 3 show the representative axial and lateral stress-strain curves of the granite specimen with 2:1 H/W ratio. Noted that, an inflection point (point A) marked the changing of two stress paths. According to the elastic mechanics theory, the slope of the axial stress-axial strain curves OA and AB can be attained, and they were 1.69 GPa and 29.64 GPa, respectively. The difference was due to changes in the stress path. In the OA stage, the axial stress and confining pressure were simultaneously loaded-unloaded to the specific values. In the AB stage, the confining pressure was kept unchanged and the axial stress continued to increase until specimen failure. In addition, an inflection point A was just the point of stress path change. A small stress before the point A produced a large deformation, and the axial deformation increased slowly after point A. ZHU et al [34] carried out the cyclic loading-unloading test with ten standard granite specimens, and reported the stress relationship is also pseudo elastic when the specimen was loaded and unloaded during the pseudo elastic phase, and an inflection point also existed on the axial stress-strain curve (see Figure 16).

Figure 14 Energy evolution curves of granite specimen with 1:1 H/W ratio in different directions (confining pressure=25 MPa):
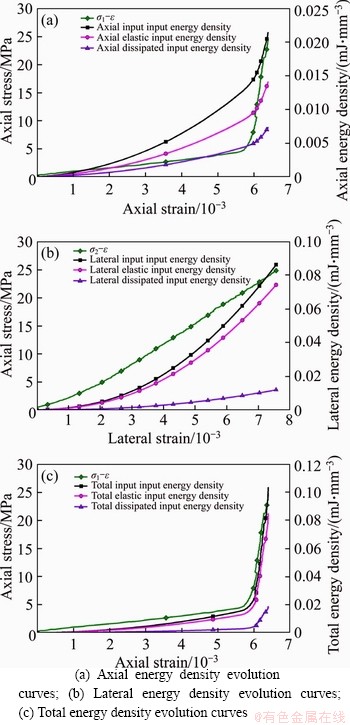
Figure 15 Energy evolution curves of granite specimen with 2:1 H/W ratio in different directions (confining pressure=25 MPa):
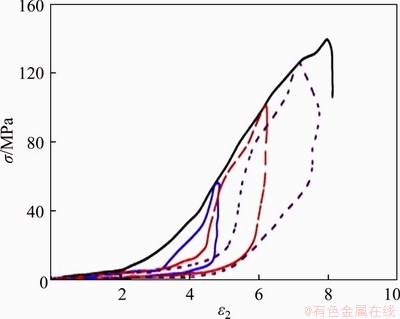
Figure 16 Cyclic loading-unloading stress-strain curves for granite specimens [34]
To better show the difference between the granite with two H/W ratios (1:1 and 2:1), based on the linear storage law in different directions (see Section 4.4), we attained the energy density parameters at the specific confining pressure, as illustrated in Figures 17, 18 and 19. As noted in Figures 17(a) and (b), as the confining pressure increases from 5 to 15 MPa, the AIED and AEED of the granite with 2:1 ratio increase at a faster rate. However, When the confining pressure increases from 15 to 25 MPa, the AIED and AEED of the granite with 1:1 ratio increases at a faster rate.
Figures 18(a) and (b) clearly shows that as the confining pressure increases, the LIED and LEED of the 2:1 H/W increase faster. Figures 19(a) and (b) also have the same law. The influence of the specimen’s H/W ratio on energy characteristics has been investigated by researchers. ZHAO and CAI [35] reported that the specimen with 1:1 H/W ratio released more energy than the specimen with 2.5:1 H/W ratio under true-triaxial unloading conditions. This is because the strength of the specimen with 1:1 H/W ratio is higher than that of granite specimen with 2.5:1 H/W ratio under true-triaxial unloading conditions, and the rock specimen’s strength is higher, more strain energy have been stored in the specimen. In the current study, when the confining pressure is 25 MPa, the strength of the specimen with 1:1 and 2:1 H/W ratio are 221.8 and 186.0 MPa, respectively. However, the total strain energy stored in the specimen with 1:1 H/W is less than that of the specimen with 2:1 ratio. Noted that, the TEED of the specimen with 1:1 and 2:1 H/W ratio was calculated under specific confining pressure, not the TEED at the peak compressive strength. Although the TEED at peak strength have not been determined, fortunately, the linear energy storage law of granite under two-dimensional constant confining pressure compression have been confirmed. Furthermore, under the two-dimensional compression, the energy evolution characteristics and peak energy density of granite in different paths can be explored.

Figure 17 Comparison of axial energy densities of specimens with two H/W ratios:

Figure 18 Comparison of lateral energy densities of specimens with two H/W ratios:
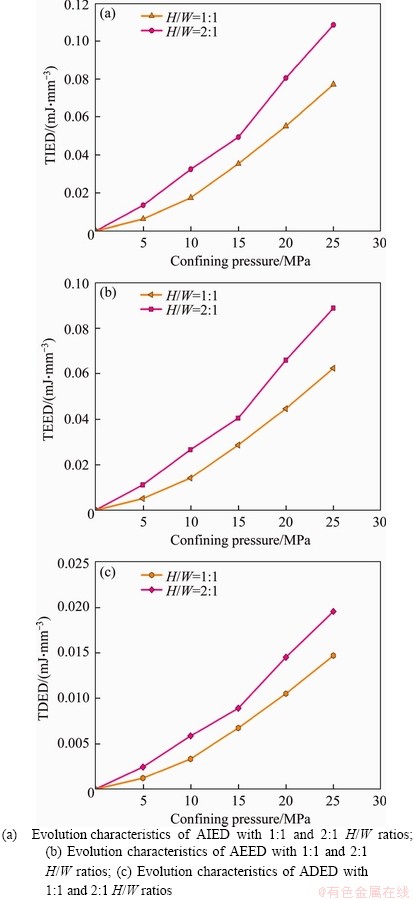
Figure 19 Comparison of total energy densities of the specimens with two H/W ratios:
6 Conclusions
To investigate the energy storage and dissipation characteristics of granite under two- dimensional constant confining pressure compression, the SCLUTDC tests were performed on the granite specimens with two H/W ratios in this study. Based on the analysis of experimental results from an energy perspective, the following conclusions were drawn:
1) Whether the H/W ratio is 1:1 or 2:1, the IED, EED and DED in the axial and lateral directions of granite specimens increase nonlinearly with increasing confining pressure as quadratic polynomial functions, so are the TIED, TEED and TDED. The EED curve is considerably similar to the corresponding IED curve in various directions, whereas the corresponding DED curve deviates farther from them.
2) Whether the H/W ratio is 1:1 or 2:1, the EED in the axial and lateral directions increase linearly with an increase in the corresponding IED, and the TEED also increases linearly as the corresponding TIED increases. A linear energy storage law is confirmed under two-dimensional constant confining pressure compression, and the H/W ratio of granite specimens not affects the linear storage law. On this basis, the CESC in various directions is introduced to describe the energy storage performance under two-dimensional constant confining compression. When the H/W ratio varies from 1:1 to 2:1, the LCESC increases and the corresponding ACESC decreases, while the TCESC is almost independent of the H/W ratio.
Contributors
GONG Feng-qiang provided the concept, developed the overarching research goal, and led the research activity planning and execution. GONG Feng-qiang also made great contribution to the improvement of manuscript after the initial draft finished. SU You-qiang conducted the experiments, analyzed the test data, and wrote the initial draft of the manuscript. LUO Song offers some valuable suggestions for the contents of the manuscript and edited the language of the manuscript. LIU Zhi-xiang reviewed and edited the manuscript. All authors replied to reviewers’ comments and revised the final version.
Conflict of interest
SU You-qiang, GONG Feng-qiang, LUO Song, and LIU Zhi-xiang declare that they have no conflict of interest.
References
[1] LI X B, GONG F Q, TAO M, DONG L J, DU K, MA C D, ZHOU Z L, YIN T B. Failure mechanism and coupled static-dynamic loading theory in deep hard rock mining: A review [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2017, 9(4): 767-782. DOI: 10.1016/j.jrmge. 2017.04.004.
[2] SI X F, GONG F Q. Strength-weakening effect and shear-tension failure mode transformation mechanism of rockburst for fine-grained granite under triaxial unloading compression conditions [J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 131: 104347. DOI: 10.1016/j.ijrmms.2020.104347.
[3] SAHOURYEH E, DYSKIN A V, GERMANOVICH L N. Crack growth under biaxial compression [J]. Engineering Fracture Mechanics, 2002, 69(18): 2187-2198. DOI: 10.1016/S0013-7944(02)00015-2.
[4] MA C D, LI X B, CHEN F, XU J C. Fracturing behavior study of biaxial compression of rock subjected to dynamic disturbance load [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(6): 1238-1244. DOI: CNKI:SUN: YSLX.0.2010-06-021. (in Chinese)
[5] LI A, SHAO G J, LEI D, ZHU Y H. Study on damage characteristics of marble under biaxial compression [J]. Journal of Hydraulic Engineering, 2012, 43(S1): 131-134. DOI: 10.13243/j.cnki.slxb.2012.s1.021. (in Chinese)
[6] ZHONG Z B, DENG R G, XIAO W M, LIN F, FU X M. Experimental study on an arched opening with straight wall in hard rhyolite under biaxial test [J]. Journal of the China Railway Society, 2016, 38(8): 110-118. DOI: 10.3969/ j.issn.1001-8360.2016.08.016. (in Chinese)
[7] PENG J Y, LI Y H, ZHANG F P, QIU Z G. Failure process and mechanism of sandstone under combined equal biaxial static compression and impact loading [J]. Strain, 2018, 54(2): e12267. DOI: 10.1111/str.12267.
[8] LIU K, ZHAO J, WU G, MAKSIMENKO A, HAQUE A, ZHANG Q B. Dynamic strength and failure modes of sandstone under biaxial compression [J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 128: 104260. DOI: 10.1016/j.ijrmms.2020.104260.
[9] XIE H P, PENG R D, JU Y. Energy dissipation of rock deformation and fracture [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(21): 3565-3570. DOI: 10.1016/j.jnucmat.2004.03.002. (in Chinese)
[10] HUANG D, LI Y R. Conversion of strain energy in triaxial unloading tests on marble [J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 66(1): 160-168. DOI: 10.1016/j.ijrmms.2013.12.001.
[11] HE M M, HUANG B Q, ZHU C H, CHEN Y S, LI N. Energy dissipation-based method for fatigue life prediction of rock salt [J]. Rock Mechanics and Rock Engineering, 2018, 51(5): 1447-1455. DOI: https://doi.org/10.1007/ s00603-018-1402-8.
[12] ZHANG Y, FENG X T, ZHANG X W, WANG Z F, SHARIFZADEH M, YANG C X, KONG R, ZHAO J. Strain energy evolution characteristics and mechanisms of hard rocks under true triaxial compression [J]. Engineering Geology, 2019, 260: 105222. DOI: https://doi.org/10.1016/ j.enggeo.2019.105222.
[13] MCSAVENEY M J, DAVIES T R. Surface energy is not one of the energy losses in rock comminution [J]. Engineering Geology, 2009, 109: 109-113. DOI: 10.1016/j.enggeo. 2008.11.001.
[14] HASHEMI S S, MELKOUMIAN N. A strain energy criterion based on grain dislodgment at borehole wall in poorly cemented sands [J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 87: 90-103. DOI: 10.1016/j.ijrmms.2016.05.013.
[15] MUNOZ H, TAHERI A, CHANDA E K. Fracture energy-based brittleness index development and brittleness quantification by pre-peak strength parameters in rock uniaxial compression [J]. Rock Mechanics and Rock Engineering, 2016, 49(12): 4587-4606. DOI: 10.1007/ s00603-016-1071-4.
[16] MAHANTA B, TRIPATHY A, VISHAL V, SINGH TN, RANJITH PG. Effects of strain rate on fracture toughness and energy release rate of gas shales [J]. Engineering Geology, 2016, 218: 39-49. DOI: 10.1016/j.enggeo.2016. 12.008.
[17] PAN Xiao-hua, LU Qing. A quantitative strain energy indicator for predicting the failure of laboratory-scale rock samples: Application to shale rock [J]. Rock Mechanics and Rock Engineering, 2018, 51(9): 2689-2707. DOI: 10.1007/ s00603-018-1480-7.
[18] GONG F Q, YAN J Y, LI X B. A new criterion of rock burst proneness based on the linear energy storage law and the residual elastic energy index [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(9): 1993-2014. DOI: CNKI:SUN:SLSK.0.2018-09-009. (in Chinese)
[19] KIVI I R, AMERI M, MOLLADAVOODI H. Shale brittleness evaluation based on energy balance analysis of stress-strain curves [J]. Journal of Petroleum Sci & Engineering, 2018, 167: 1-19. DOI: 10.1016/j.petrol. 2018.03.061.
[20] LI Y R, HUANG D, LI X A. Strain rate dependency of coarse crystal marble under uniaxial compression: Strength, deformation and strain energy [J]. Rock Mechanics and Rock Engineering, 2014, 47(4): 1153-1164. DOI: 10.1007/ s00603-013-0472-x.
[21] HOU P, GAO F, YANG Y G, ZHANG X X, ZHANG Z Z. Effect of the layer orientation on mechanics and energy evolution characteristics of shales under uniaxial loading [J]. International Journal of Mining Science and Technology, 2016, 26(5): 857-862. DOI: 10.1016/j.ijmst.2016.05.041.
[22] MUNOZ H, TAHERI A, CHANDA E K. Rock drilling performance evaluation by an energy dissipation based rock brittleness index [J]. Rock Mechanics and Rock Engineering, 2016, 49(8): 3343-3355. DOI: 10.1007/s00603-016-0986-0.
[23] MENG Q B, ZHANG M W, HAN L J, PU H, NIE T Y. Effects of acoustic emission and energy evolution of rock specimens under the uniaxial cyclic loading and unloading compression [J]. Rock Mechanics and Rock Engineering, 2016, 49(10): 3873-3886. DOI: 10.1007/s00603-016- 1077-y.
[24] GONG F Q, WANG Y L, LUO S. Rockburst proneness criteria for rock materials: Review and new insights [J]. Journal of Central South University, 2020, 27(10): 2793-2821. DOI: 10.1007/s11771-020-4511-y.
[25] GONG F Q, YAN J Y, LI X B, LUO S. A peak-strength strain energy storage index for rock burst proneness of rock materials [J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 117: 76-89. DOI: 10.1016/ j.ijrmms.2019.03.020.
[26] GONG F Q, YAN J Y, LUO S, LI X B. Investigation on the linear energy storage and dissipation laws of rock materials under uniaxial compression [J]. Rock Mech Rock Eng, 2019, 52(11): 4237-4255. DOI: 10.1007/s00603- 019-01842-4.
[27] LI L Y, WANG R X, MA X, ZHAO Z W, XU Y Y, LU J F. The energy variety analysis of rock under biaxial compression [J]. Journal of China Coal Society, 2010, 35(12): 2033-2038. DOI: 10.1016/S1876-3804(11)60004-9. (in Chinese)
[28] WANG Y F, ZHENG X J, WANG L P, ZHOU H B. Energy evolution mechanism in failure process of coalrock and energy strength criterion under biaxial loading [J]. Industrial Construction, 2015, 45(5): 87-92, 110. DOI:10. 13204/ j.gyjz201505019. (in Chinese)
[29] YANG Y F, TANG C A, XIA K W. Study on crack curving and branching mechanism in quasi-brittle materials under dynamic biaxial loading [J]. International Journal of Fracture, 2012, 177(1): 53-72. DOI: 10.1007/s10704-012-9755-6.
[30] FAIRHURST C E, HUDSON J A. Draft ISRM suggested method for the complete stress-strain curve for intact rock in uniaxial compression [J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(3): 281-289. DOI: 10.1016/S0148-9062(99)00006-6.
[31] MOGI K. Experimental rock mechanics [M]. London: Taylor & Francis Group, 2007.
[32] AMADEI B, ROBINSON M J. Strength of rock in multiaxial loading conditions [C]// Proceedings of 27th US Rock Mech Symposium. Alabama: Tuscaloosa. 1983, 47-55. https://www.researchgate.net/publication/254543007.
[33] LIANG C Y, ZHANG Q B, LI X, XIN P. The effect of specimen shape and strain rate on uniaxial compressive behavior of rock material [J]. Bulletin of Engineering Geology and the Environment, 2016, 75(4): 1669-1681. DOI: 10.1007/s10064-015-0811-0.
[34] ZHU W S, YANG W M, LI X J, XIANG L, YU D J. Study on splitting failure in rock masses by simulation test, site monitoring and energy model [J]. Tunnelling and Underground Space Technology, 2014, 41: 152-164. DOI: 10.1016/j.tust.2013.12.007.
[35] ZHAO X G, CAI M. Influence of specimen height-to-width ratio on the strainburst characteristics of Tianhu granite under true-triaxial unloading conditions [J]. Canadian Geotechnical Journal, 2014, 52(7): 890-902. DOI: 10.1139/cgj-2014-0355.
(Edited by HE Yun-bin)
中文导读
二维等围压压缩下花岗岩的能量存储和耗散特征试验研究
摘要:为了研究深部岩石在二维等围压压缩下的能量存储和耗散特征,对两种高宽比(1:1和2:1)的长方体花岗岩试样进行了五种围压下的一次加卸载压缩试验。利用图形积分方式获得了试样在五种围压下的轴向和侧向的输入能密度、弹性能密度和耗散能密度的值。试验结果表明:两种高宽比下试样的三种能量密度参数值随着围压的增加而非线性增加,呈现二次多项式函数关系;在二维等围压压缩下,发现了轴向和侧向上的线性储能规律。根据轴向和侧向上的线性储能规律,可以计算花岗岩在具体围压下轴向、侧向以及总的弹性能密度的值。此外,当高宽比从1:1增加到2:1时,侧向压缩储能系数增加,相应的轴向压缩储能系数降低,而总的压缩储能系数与高宽比无关。
关键词:岩石力学;二维压缩;线性储能规律;一次加卸载;高宽比
Foundation item: Projects(41877272, 51974359) supported by the National Natural Science Foundation of China
Received date: 2020-06-30; Accepted date: 2020-10-09
Corresponding author: GONG Feng-qiang, PhD, Professor; Tel: +86-18175973819; E-mail: fengqiangg@126.com; ORCID: https:// orcid.org/0000-0002-2040-4294
Abstract: To study the energy storage and dissipation characteristics of deep rock under two-dimensional compression with constant confining pressure, the single cyclic loading-unloading two-dimensional compression tests were performed on granite specimens with two height-to-width (H/W) ratios under five confining pressures. Three energy density parameters (input energy density, elastic energy density and dissipated energy density) in the axial and lateral directions of granite specimens under different confining pressures were calculated using the area integral method. The experimental results show that, for the specimens with a specific H/W ratio, these three energy density parameters in the axial and lateral directions increase nonlinearly with the confining pressure as quadratic polynomial functions. Under constant confining pressure compression, the linear energy storage law of granite specimens in the axial and lateral directions was founded. Using the linear energy storage law in different directions, the elastic energy density in various directions (axial elastic energy density, lateral elastic energy density and total elastic energy density) of granite under any specific confining pressures can be calculated. When the H/W ratio varies from 1:1 to 2:1, the lateral compression energy storage coefficient increases and the corresponding axial compression energy storage coefficient decreases, while the total compression energy storage coefficient is almost independent of the H/W ratio.


