Trans. Nonferrous Met. Soc. China 22(2012) 1701-1710
Determination of energy coupling to material in laser welding by a novel “sandwich” method
ZHANG Yi, SHI Ru-kun, LI Li-jun
State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China
Received 18 April 2012; accepted 15 June 2012
Abstract:
A mathematical energy coupling model was developed to analyze the light transmission in the keyhole and energy distribution on the keyhole wall. The main characteristics of the model include: 1) a prototype of the keyhole and the inverse Bremsstrahlung absorption coefficient in the keyhole plasma are obtained from the experiments; 2) instead of using a parallel incident beam, a focused laser beam with real Gaussian intensity distribution is implemented; 3) both Fresnel absorption and inverse Bremsstrahlung absorption during multiple reflections are considered. The calculation results show that the distribution of absorbed laser intensity by the keyhole wall is not uniform. The maximum laser energy is absorbed by the bottom of the keyhole, although no rays irradiate directly onto the bottom. According to analysis of beam focusing characteristics, the location of the focal plane plays a more important role in the laser energy absorption by the front wall than by the rear wall.
Key words:
laser welding; mathematical energy coupling model; “sandwich” method; keyhole;
1 Introduction
As a joining technique, laser welding is being applied in the metal industry on an increasing scale. Laser welding is generally classified as either conduction or keyhole welding. The basic difference between two classifications is the appearance of the keyhole. The role of the keyhole is predominant but the mechanism of the keyhole is complex and not fully understood. The mechanism of keyhole welding involves keyhole formation, plasma generation, energy coupling to the material, solid-liquid and liquid-gas phase transitions, the delicate balance between heating and cooling, the stability of keyhole, the effects of process parameters on welding quality and so on.
In order to make laser welding more efficient, it is necessary to couple as much incident intensity to the material as possible. Energy absorption by the keyhole wall due to multiple reflections is quite different from the incident flux. Fresnel absorption and inverse Bremsstrahlung (IB) absorption are two dominant mechanisms for energy coupling to material in laser welding as proposed in the literature. Generally, Fresnel absorption is even more influential than IB absorption in the keyhole [1]. Therefore, only the Fresnel absorption was considered in some models for simplicity [2-5]. The rays are trapped in the keyhole and ray tracing techniques are briefly implemented to describe Fresnel absorption and multiple reflections. On the other hand, the keyhole is indeed filled with partially ionized plasma in laser welding of metal materials. Laser energy is transferred to the plasma by means of inverse Bremsstrahlung absorption, and is then transported elsewhere by both reradiation and thermal conduction. IB absorption due to keyhole plasma plays a significant role in coupling laser energy to the materials [6,7]. Beer-Lambert’s law is the simplest approach to describe IB absorption [8-11]. The IB absorption coefficient can be obtained from single temperature plasma under the atmospheric pressure [12,13].
To analyze beam absorption by the keyhole wall, the keyhole profile should be either calculated simultaneously [14-16] or known in advance [17]. Some researchers tracked the light transmission based on the assumption of a cylindrical or conical keyhole shape [18], which is only valid at low welding speeds. In fact, for keyhole welding with high laser speeds, neither the shape of the keyhole is rotationally symmetric, nor the centre line of the keyhole is straight. The keyhole is bent in the opposite direction of the beam travel velocity. The higher the laser speed is, the larger the bending angle occurs. A rapid CCD camera located coaxially to the laser beam is an effective way to record the shape of the keyhole on the workpiece surface, in particular to record the keyhole’s diameter. Owing to those convenient observations, the two-dimensional images of the keyhole shape from the top view can be used extensively in analysis of keyhole behavior [5,19,20]. Although it is difficult to observe the shape of the keyhole perpendicular to the workpiece surface, more information about the keyhole can be obtained from the side view of the keyhole [1,21].
Initially, the incident intensity distribution of laser was assumed to move a line source of heat [22]. In recent years, the more accurate heat source with the Gaussian or uniform top-hat distribution [11] has been widely used in the mathematic model to simulate energy absorption. However, a parallel incident beam is usually taken when considering the irradiation on the keyhole wall. This simplification is far from the actual condition in laser welding.
In order to study the energy coupling between laser and material during laser welding, a focused laser beam with real Gaussian intensity distribution is implemented in the present work, instead of using a parallel incident beam. Both Fresnel absorption and IB absorption are considered.
2 Experimental
A specially designed setup shown in Fig. 1 was used to observe the keyhole and take measurements of the light emission of the keyhole plasma in deep penetration laser welding of aluminum films, clamped between two pieces of GG17 glass. This kind of experimental sample [23] is called a “sandwich”. The laser beam was focused to a diameter of about 0.3 mm by a GaAs lens with a focal length of 100 mm. Coaxial shielding Ar gas was used to blow off the plasma plume and to protect the lens and the weld bead. On one side of the sandwich sample, a high-speed camera was used to take photographs, the exposure of which was 1/1000 s. In order to attenuate the high-temperature light emission, a filter was placed in front of the camera. On the other side, a spectrometer and a CCD camera were employed to take spectral analysis of light emission inside the keyhole during laser welding. All experimental data were recorded and saved in the computer. The laser used was a specially designed PHC-1500 CO2 CW laser with a folded resonator. The transverse mode of the output beam was near Gaussian. In all of the experiments, the beam was kept stationary while the specimen was moved by a CNC controlled worktable.
Fig. 1 Schematic diagram of experimental setup
3 Energy coupling model
3.1 Characteristics of model
As is known, the energy coupling between laser and material during laser welding is determined by Fresnel absorption due to multiple reflections and inverse Bremsstrahlung absorption due to keyhole plasma. The formation of the keyhole makes the welding pool deeper and narrower, improving the efficiency of laser energy absorption. In order to analyze the light transmission in the keyhole and energy distribution on the keyhole wall, the energy coupling model was characterized as follows.
1) The prototype of the keyhole described in the model was obtained in the above experiment. Based on the observation of Fig. 2(a) the fitted curve of the keyhole was obtained as shown in Fig. 2 (b). Then the front wall and the rear wall of the keyhole can be formulated by the following function.
For the front wall, there is
(1)
For the rear wall, there is
(2)
where a1, a2, a3 and a4, b1, b2, b3 and b4 are the polynomial coefficients for the front and rear keyhole wall, respectively.
2) A focused incident flux of Gaussian distribution was implemented in the system model to investigate the beam characteristics, and the focused spot was taken as that emitted by a visual focal point O illustrated in Fig. 3. For the radius of the real focal spot is r0 and a visual focal point with the zero radius is defined in order to trace the light ray. In the model, the focused laser beam can be absorbed and reflected. The distance between the focused spot and the workpiece surface is denoted by d, being positive above the surface and negative inside the keyhole. The distance between the visual focal point and the focused spot is taken as d0. Also, the diameters of the Gaussian beam and the focused spot are ωm and 2r0, respectively. In the model, a Cartesian coordinate system is used with the x-axis as the travel direction and the z-axis as the transmission direction of laser.
Fig. 2 Photograph of keyhole (a) and geometry of keyhole (b) in energy coupling model
Fig. 3 Scheme of laser welding procedure
3) Because the absorption process is considered to be in the symmetrical plane along the travel direction, laser processing can be simulated in two dimensions, as a function of main parameters such as welding speed, incident intensity, and material properties. The absorptions on the front wall and the rear wall of the keyhole during laser welding should be most concerned as they determined the geometry of the keyhole and the whole process of deep penetration laser welding.
4) Both Fresnel absorption and inverse Bremsstrahlung absorption are taken into account in the model. Fresnel absorption is very efficient inside the keyhole due to the multiple reflections of the trapped laser beam. The reflectivity, R, by the keyhole wall was mainly dependent on the angle θ between the incident ray and the surface normal as follows [24]:
(3)
(4)
where ε1, ε2 are the real parts of dielectric constants of the metal and the gas, respectively; σst is the static conductivity of the metal; ω is the laser frequency; ε0 is the vacuum permeability.
The absorption rate will be 1-R. IB absorption results from the presence of plasma inside the keyhole. The plasma absorbs the energy of the laser beam and then re-deposits the energy on the keyhole wall by radiation. An expression for the IB absorption coefficient is [25]
(5)
where ne is the electron density; e is the elementary charge; 
is the quantum mechanical Gaunt factor; me is the electron mass; 
is the Planck’s constant; kb is Boltzmann’s constant; Tp is the plasma temperature; c is the vacuum speed of light; ωpe is the plasma frequency.
3.2 Assumptions in model
The aim of the mathematical model was to understand the behavior of laser beam in the keyhole. The fundamental assumptions of the model are outlined below.
1) The process is considered to be in the quasi-stationary state, which is reasonable when the laser heat source is moving at a constant speed on a regular path.
2) Reflections by the keyhole wall are assumed to be specular in character, following the classic Fresnel rule with the angle of incidence θinc equal to the angle of reflection θref, which has been widely accepted for deciding the material’s laser absorption rate.
3) The laser source represented by the Gaussian intensity distribution and the keyhole profile are both discretized as shown in Fig. 4. The Gaussian beam intensity perpendicular to the focusing beam at r on the lens is
(6)
where P is the power of laser beam. For the high power laser used in the experiments, the beam quality factor M2 was measured to be 1.26, which was closely achieved for a diffraction-limited Gaussian beam. The approach is thus expected to give a useful approximation.
Fig. 4 Discretization of laser source and keyhole
4) To calculate the absorption of incident laser light in the keyhole plasma, it is assumed that the electron temperature distribution is uniform. The electron temperature and density of the plasma are measured in the experiments. Although it is much more complicated in reality, the absorbed intensity from the inverse Bremsstrahlung absorption Iabsp is well described by Beer-Lambert's Law. In Eq. (7), 
is the inverse Bremsstrahlung absorption rate, z is the distance the laser travels through the plasma, and Iinc is the incident intensity of the laser.
(7)
3.3 Energy absorption by keyhole wall
In laser welding, especially deep penet1ration laser welding, it is critical to understand the mechanism of energy coupling between laser and materials, as well as keyhole formation and plasma generation. In keyhole laser welding, the incident laser intensity is affected by several phenomena including plasma plume damping, multiple reflection and absorption, and inverse Bremsstrahlung absorption due to keyhole plasma. In this work, a ray tracing technique with a discrete grid cell system was proposed to simulate the energy transportation. The basic point was that the laser beam consisted of a bundle of ray, and then the ray was trapped by ray tracing technique to determine the trajectory in the keyhole.
3.3.1 Angles of incidence and reflection
The local inclination of the keyhole wall on the wall segment (i, i+1) is defined by (βe)i with respect to the x-axis direction, while its normal angle is referred to as (βnor)i normal to the segment. Each ray j incident on the keyhole wall for the kth time on the wall segment (i, i+1) with an angle 
is reflected with an angle 
, both angles measured with respect to the x-axis direction. For this definition, when
gives
(8)
And according to assumption 2,
(9)
(10)
Based on the profile feature of the keyhole in experiments, the incident angle, 
, of the ray j and the angle of the reflected ray j,
can be determined in the following six cases shown in Fig. 5.
Case 1 For the ray j incident on the rear wall segment (i, i+1) and 
, 
,
(11)
Case 2 For the ray j incident on the rear wall segment (i, i+1) and 
, 
,
(12)
Case 3 For the ray j incident on the rear wall segment (i, i+1) and , ,
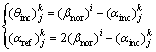(13)
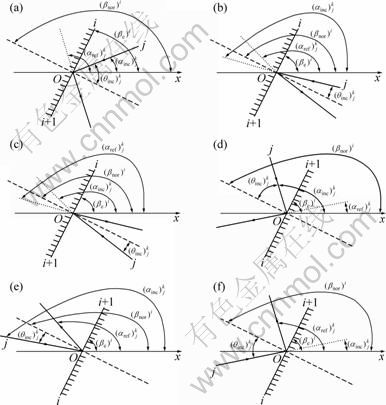
Fig. 5 Reflection of ray j on segment (i, i+1) for the kth time: (a) k=1; (b) k=2; (c) k=3; (d) k=4; (e) k=5; (f) k=6
Case 4 For the ray j incident on the front wall segment (i, i+1) and , ,
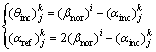(14)
Case 5 For the ray j incident on the front wall segment (i, i+1) and , ,.
(15)
Case 6 For the ray j incident on the front wall segment (i, i+1) and , ,
(16)
3.3.2 Equation of incident ray j
As shown in Figs. 2 and 3, the slope of ray j incident on the keyhole wall for the first time can be formulated as:
(17)
where F is the focal length of the lens used in the experiments, and rj is the location of the ray j on the lens.
Then the equation of ray j incident on the keyhole wall for the first time is described as:
(18)
with
(19)
Combining Eqs. (1), (2) and (18), the first incident point (
,
) on the keyhole wall is obtained.
If the (k-1)th incident point (
,
) is known, then the equation of ray j incident on the keyhole wall for the (k-1)th time can be expressed as:
(20)
with
(21)
For 
, combining Eqs. (1), (2) and (20), the kth incident point (
,
) on the keyhole wall is identified.
3.3.3 Power density of incident ray j
The power of each ray is described from a circularly symmetric Gaussian beam profile as:
(22)
Nevertheless, the intensity varies in inverse proportion to the square of the light path difference between the source and the surface, according to the inverse square law of the photometry. If the influence of plasma is ignored, the intensity of each incident light should be written as Eq. (23) before it first arrives on the keyhole wall.
(23)
Also, the plasma plume exits above the keyhole and the keyhole contains partially ionized keyhole plasma during laser welding of metal materials. The laser beam transports partial energy to the inverse Bremsstrahlung, and which is then transferred by both reradiation and thermal conduction. Therefore, beam damping due to plasma plume and inverse Bremsstrahlung absorption because of keyhole plasma should not be neglected. The intensity of each light before reaching the keyhole wall can be expressed as:
(24)
with
(25)
Equation (24) represents the power density 
of ray j incident on the keyhole wall for the first time. In order to obtain both Fresnel absorption and IB absorption thanks to each reflection on the keyhole wall, the power density 
of ray j incident on the keyhole wall for the kth (k≥2) time is expressed as:
(26)
Combining Eqs. (24) and (26), the final expression of the power density of ray j incident on the keyhole wall for the kth time can be given as:
(27)
3.3.4 Absorbed intensity by keyhole wall
Based on assumption 4, IB absorption of ray j uniformly reradiates and transports energy to the nodes in the rectangle area [
，
], as shown in Fig. 6. Then the power density owing to IB absorption of ray j by node i can be expressed as:
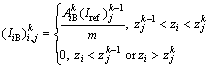(28)
where 
is the power density of ray j after the (k-1)th reflection by the keyhole wall, m is the number of nodes in the rectangle area [，], and 
is the absorption coefficient due to IB absorption.
Fig. 6 Schematic of IB absorption of ray j for the kth time
The power density due to Fresnel absorption of ray j by node i can be expressed as:
(29)
where 
is the absorption coefficient due to Fresnel absorption.
The power density due to both Fresnel absorption and IB absorption of ray j by node i can be expressed as:
(30)
Thus, the total absorbed power density by node i can be expressed as:
(31)
where li is the length of segment on the keyhole wall.
A flow chart depicted in Fig. 7 shows the laser beam coupling to the materials based on the keyhole in the experiments.
4 Results and discussion
The above mentioned mathematical model is used to study the effects of energy distribution on Fresnel absorption, IB absorption, and the location of the focal plane. The results for laser welding with a spatially Gaussian continuous wave CO2 laser are given here. The laser processing parameters are listed as follows: laser beam power P=1000 W; focal length of GaAs lens F=100 mm; the diameter of the laser beam before focusing ωm=30 mm; the radius of the focal spot r0=0.15 mm. The aluminum spectrum in the experiment is shown in Fig. 8.
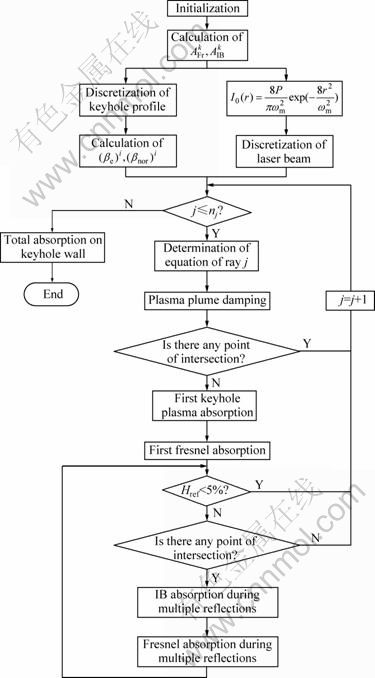
Fig. 7 Flow chart of absorption mechanism in laser welding
First, only the Fresnel absorption by both the front wall and the rear wall was calculated during multiple reflections. The result is shown in Fig. 9, and it is indicated that the distribution of the absorbed laser intensity is not uniform for the Fresnel absorption. As the keyhole is bent, it is not possible for the laser to irradiate directly on the entire keyhole wall, especially on the rear wall of the keyhole. For Fresnel absorption on the keyhole wall investigated, the magnitude of average absorbed laser intensity by the rear wall was 105 W/m2, while the average absorbed laser intensity by the front wall was 108 W/m2. Although no rays directly irradiated on the bottom of the keyhole, the maximum laser energy was absorbed by the bottom of the keyhole due to Fresnel absorption during multiple reflections, which was caused by the minimum curvature radius at the bottom of keyhole wall.
IB absorption was also calculated in order to reveal the effects of IB absorption on the keyhole wall. Comparing Fig. 9 and Fig. 10, it is demonstrated that IB absorption changes the distribution of the energy absorption by the whole keyhole wall, especially by the rear wall. The magnitude of average absorbed laser intensity by the rear wall increases by 10 times compared with that under neglecting IB absorption, reaching up to 106 W/m2. However, IB absorption only plays a small role in the total absorption by the front wall. The greatest contribution of the energy absorption by the front wall is made by Fresnel absorption during multiple reflections. Similar to the results shown in Fig. 9, the maximum laser energy is absorbed by the bottom of the keyhole when considering both Fresnel absorption and IB absorption by the keyhole wall.
Fig. 8 Aluminum spectrum in experiment
Fig. 9 Fresnel absorption by keyhole wall during multiple reflections
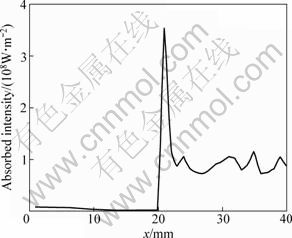
Fig. 10 Total absorption by keyhole wall during multiple reflections
As an important process parameter, the location of the focal plane not only changes the beam diameter on the workpiece surface, but also alters the sidescattering of incident light, resulting in variation of distribution of energy absorption on the keyhole wall. Using the ray-tracing procedure introduced previously, local energy depositions on the keyhole wall under different locations of focal plane were calculated. The distance d between the focal plane and workpiece surface shown in Fig. 11 is taken to be negative when the focal plane is inside the sample or positive when the focal plane is above the sample surface. From Fig. 11, it is indicated that the location of the focal plane plays a more important role in laser energy absorption by the front wall than by the rear wall. This is because the greatest contribution of laser energy absorption by the rear wall is made by IB absorption, while Fresnel absorption is the main mechanism of laser energy absorption by the front wall during multiple reflections. The location of the focal plane has great effect on Fresnel absorption by the keyhole, by changing beam diameter and direction of the incident laser beam, which can be seen in Fig. 11. When the focal plane is above the sample surface, the power density irradiated on the keyhole wall is reduced, so the total absorbed laser intensity decreases. When the focal plane is inside the sample, the power density irradiated on the keyhole wall is higher, so the total absorbed laser intensity increases.
Fig. 11 Absorption by keyhole wall under different locations of focal plane
5 Conclusions
1) By observation of an actual keyhole in laser welding of thin aluminum foil clamped between two pieces of glass, it is found that the keyhole is seriously bent in the opposite direction of the welding speed. Based on the novel “sandwich” experimental method, a mathematical energy coupling model has been developed to analyze the light transmission in the keyhole and energy distribution on the keyhole wall. By trapping the rays of the laser beam, the trajectory of the light in the keyhole was determined by a ray-tracing technique. Then the incident angle, the incident point on the keyhole wall, the equation of the incident ray, the equation of the reflected ray, and the energy distribution of the absorbed laser intensity by the keyhole wall were obtained. As the keyhole is bent, it is not possible for the laser to irradiate directly on the entire keyhole wall. Therefore, the distribution of absorbed laser intensity by the keyhole wall was not uniform. It is interesting that the maximum laser energy is absorbed by the bottom of the keyhole due to both Fresnel absorption and IB absorption during multiple reflections, although no rays are directly irradiated onto the bottom. Also, the magnitude of average absorbed laser intensity by the front wall is one thousand times more than that by the rear wall.
2) Fresnel absorption and inverse Bremsstrahlung (IB) absorption are two basic alternative mechanisms for energy transfer in deep penetration laser welding. According to the calculations, the greatest contribution of laser energy absorption by the rear wall is made by IB absorption, while Fresnel absorption is the main mechanism of laser energy absorption by the front wall during multiple reflections. Therefore, the location of the focal plane plays a more important role in laser energy absorption by the front wall than by the rear wall. Defocus not only changes the beam diameter on the workpiece surface but also alters the sidescattering of incident lights, resulting in varied distribution of energy absorption by the keyhole wall.
References
[1] MIZUTANI M, KATAYAMA S, MATSUNAWA A. Observation of molten metal behavior during laser irradiation: Basic experiment to understand laser welding phenomena [C]//Proceedings of SPIE. First International Symposium on High-power Laser Macroprocessing. Osaba: 2003, 4831: 208.
[2] CHENG Yuan-yong, JIN Xiang-zhong, LI Shi-chun, ZENG Li-cheng. Fresnel absorption and inverse Bremsstrahlung absorption in an actual 3D keyhole during deep penetration CO2 welding of aluminum 6016 [J]. Optics & Laser Technology, 2012, 44: 1426-1436.
[3] KAPLAN A F H. Fresnel absorption of 1 μm- and 10 μm-laser beams at the keyhole wall during laser beam welding: Comparison between smooth and wavy surfaces [J]. Applied Surface Science, 2012, 258: 3354-3363.
[4] WWAN-WOO P. Theoretical investigations on multiple-reflection and Rayleigh absorption-emission-scattering effects in laser drilling [J]. Applied Surface Science, 2010, 256: 2392-2399.
[5] LEE J Y, SUNG H K, FARSON D F, CHOONG D Y. Mechanism of keyhole formation and stability in stationary laser welding [J]. J Phys D: Appl Phys, 2002, 35: 1570-1576.
[6] FABBRO R. Melt pool and keyhole behaviour analysis for deep penetration laser welding [J]. J Phys D: Appl Phys, 2010, 43: 445501-9.
[7] DOWDENT J, WU S C, KAPADIAS P, STRANGELL C. Dynamics of the vapour flow in the keyhole in penetration welding with a laser at medium welding speeds [J]. J Phys D: Appl Phys, 1991, 24: 519-532.
[8] ZHANG Yi, LI Li-jun, ZHANG Gang. Spectroscopic measurements of plasma inside the keyhole in deep penetration laser welding [J]. J Phys D: Appl Phys, 2005, 38: 703-710.
[9] AMARA E H, BENDIB A. Modelling of vapour flow in deep penetration laser welding [J]. J Phys D: Appl Phys, 2002, 35: 272-280.
[10] ZHOU J, TSAI H L, WANG P C. Transport phenomena and keyhole dynamics during pulsed laser welding [J]. J Heat Transfer, 2006, 128: 680-690.
[11] FABBRO R, CHOUF K. Keyhole modeling during laser welding [J]. J Appl Phys, 2000, 87: 4075-4083.
[12] SOLANA P, NEGRO G. A study of the effect of multiple reflections on the shape of the keyhole in the laser processing of materials [J]. J Phys D: Appl Phys, 1997, 30: 3216-3222.
[13] SOLANA P, OCANA J L. A mathematical model for penetration laser welding as a free-boundary problem [J]. J Phys D: Appl Phys, 1997, 30: 1300-1314.
[14] FABBRO R, SLIMANI S, DOUDET I, COSTE F, BRIAND F. Experimental study of the dynamical coupling between the induced vapour plume and the melt pool for Nd-Yag CW laser welding [J]. J Phys D: Appl Phys, 2006, 39: 394-400.
[15] ABDERRAZAK K, BANNOUR S, MHIRI H, LEPALEC G, AUTRIC M. Numerical and experimental study of molten pool formation during continuous laser welding of AZ91 magnesium alloy [J]. Computational Materials Science, 2009, 44: 858-866.
[16] FABBRO R, SLIMANI S, COSTE F, BRIAND F. Study of keyhole behaviour for full penetration Nd–Yag CW laser welding [J]. J Phys D: Appl Phys, 2005, 38: 1881-1887.
[17] CHO J H, NA S J. Implementation of real-time multiple reflection and Fresnel absorption of laser beam in keyhole [J]. J Phys D: Appl Phys, 2006, 39: 5372-5378.
[18] JIN X Z, BERGER P, GRAF T. Multiple reflections and Fresnel absorption in an actual 3D keyhole during deep penetration laser welding [J]. J Phys D: Appl Phys, 2006, 39: 4703-4712.
[19] MOHANTY P S, ASGHARI T, MAZUMDER J. Experimental study on keyhole and melt pool dynamics in laser welding [C]//Proc ICALEO'97. San Diego, LIA: Laser Institute of America, 1997: Section G, 200.
[20] MIYAMOTO I, OHMURA E, MAEDE T. Dynamic behavior of plume and keyhole in CO2 laser welding [C]//Proc ICALEO'97. San Diego, FL: Laser Institute of America, 1997: Section G, 210-18.
[21] MARTIN B, LOREDO A, PILLOZ M, GREVEY D. Characterisation of CWNd:YAG laser keyhole dynamics [J]. Optics & Laser Technology, 2001, 33: 201-207.
[22] KAPLAN A. A model of deep penetration laser welding based on calculation of the keyhole profile [J]. J Phys D: Appl Phys, 1994, 27: 1805-1814.
[23] ZHANG Yi, CHEN Gen-yu, WEI Hai-ying, ZHANG Jun. A novel “sandwich” method for observation of the keyhole in deep penetration laser welding [J]. Optics and Lasers in Engineering, 2008, 46(2): 133-139.
[24] SCHULZ W, SIMON G, URBASSEK H M, DECKER I. On laser fusion cutting of metals [J]. J Phys D: Appl Phys, 1987, 20: 481-488.
[25] HUGES T P. Plasmas and laser light [M]. London: Adam Hilger, 1975: 44.
基于“三明治”方法的激光焊接能量耦合模型
张 屹，史如坤，李力钧
湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082
摘 要：建立激光与能量耦合模型以研究激光在小孔内的传输和孔壁能量的分布。该模型的主要特点包括：1)小孔和孔内等离子体的逆韧致吸收系数均为实验测量所得；2) 入射激光为高斯分布的聚焦光束而非平行光束；3) 同时考虑了激光光束在孔内多次反射的菲涅尔吸收和逆韧致吸收。计算结果表明：孔壁所吸收的激光能量并不一致；尽管激光未能直接照射孔底，但是小孔孔底所吸收的激光能量最多。基于聚焦光束的特征分析，焦平面的位置对小孔前沿所吸收的激光能量较后沿更重要。
关键词：激光焊接；能量耦合模型；“三明治”方法；小孔
(Edited by YANG Hua)
Foundation item: Projects (51175162, 50805045) supported by the National Natural Science Foundation of China; Project supported by the Scientific Research Foundation for the Returned Overseas Chinese Scholars, Ministry of Education, China
Corresponding author: ZHANG Yi; Tel: +86-13787097373; E-mail: zy2100_hn@yahoo.com
DOI: 10.1016/S1003-6326(11)61376-9
Abstract: A mathematical energy coupling model was developed to analyze the light transmission in the keyhole and energy distribution on the keyhole wall. The main characteristics of the model include: 1) a prototype of the keyhole and the inverse Bremsstrahlung absorption coefficient in the keyhole plasma are obtained from the experiments; 2) instead of using a parallel incident beam, a focused laser beam with real Gaussian intensity distribution is implemented; 3) both Fresnel absorption and inverse Bremsstrahlung absorption during multiple reflections are considered. The calculation results show that the distribution of absorbed laser intensity by the keyhole wall is not uniform. The maximum laser energy is absorbed by the bottom of the keyhole, although no rays irradiate directly onto the bottom. According to analysis of beam focusing characteristics, the location of the focal plane plays a more important role in the laser energy absorption by the front wall than by the rear wall.
