A first-principle calculation of structural, mechanical and electronic properties of titanium borides

YAN Hai-yan¹, WEI Qun², CHANG Shao-mei³, GUO Ping⁴

1. Department of Chemistry and Chemical Engineering, Baoji University of Arts and Sciences, Baoji 721013, China;

2. Department of Physics, Xidian University, Xi’an 710071, China;

3. Department of Physics, Baoji University of Arts and Sciences, Baoji 721007, China;

4. Department of Physics, Northwest University, Xi’an 710069, China

Received 17 August 2010; accepted 15 November 2010

Abstract:

The first-principle calculations are performed to investigate the structural, mechanical and electronic properties of titanium borides (Ti₂B, TiB and TiB₂). Those calculated lattice parameters are in good agreement with the experimental data and previous theoretical values. All these borides are found to be mechanically stable at ambient pressure. Compared with parent metal Ti (120 GPa), the larger bulk modulus of these borides increase successively with the increase of the boron content in three borides, which may be due to direction bonding introduced by the boron atoms in the lattice and the strong covalent Ti—B bonds. Additionally, TiB can be regarded as a candidate of incompressible and hard material besides TiB₂. Furthermore, the elastic anisotropy and Debye temperatures are also discussed by investigating the elastic constants and moduli. Electronic density of states and atomic Mulliken charges analysis show that chemical bonding in these titanium borides is a complex mixture of covalent, ionic, and metallic characters.

Key words:

titanium borides; first-principle calculations; mechanical properties; density of states; Mulliken atomic population analysis;

1 Introduction

With the actual increasing interest and impetus in the search for materials possessing specific and desired properties, transition metal borides have attracted much attention for their fundamental physics and technological application [1-3]. More precisely, titanium borides (Ti₂B, TiB and TiB₂) are a group of materials with outstanding properties such as chemical stability, high hardness, high melting point, good thermal conductivity, and low electrical resistivity [4-5]. Besides bulk titanium borides, increasing attention is also devoted recently to their nano-sized forms such as nanopowders, nanowires, nanotubes, and nanocomposites [6-8].

Among these borides, the most known AlB₂-type TiB₂ is a potential candidate for many high-performance applications, in cutting tools, wear-resistant coating, electrodes in aluminum-extraction cells, etc. A great deal of experimental and theoretical effort has been performed on TiB₂ at ambient pressure as well as high pressure [9-18]. However, some previous experimental results for the measured mechanical properties are somewhat different [10, 13, 19]. Besides, by contrast, it turned out that the works (including ab initio calculations) for other borides (especially Ti₂B) are limited. So, this is one of motivations for the present work. Furthermore, to the best of our knowledge, TiB whiskers as reinforcements play an important role in various titanium alloys [20], while Ti₂B is an essentially intermetallic compound [21]. Therefore, systematic studies on the crystal structure and related physical properties of titanium borides are necessary and of great interest.

In the present work, in order to get insight to the mechanical and electronic properties of transition borides systematically, a first-principle study for Ti₂B, TiB and TiB₂ has been performed using the projector augmented wave (PAW) method. We have evaluated and analyzed a set of physical parameters of these transition borides such as lattice parameters, density of states, Mulliken charges, and mechanical properties (elastic constants, bulk and shear modulus, elastic modulus, elastic anisotropy, etc.). Additionally, the numerical estimates of sound velocities and Debye temperature of three borides were also predicted.

2 Computational methods

The first-principle calculations were performed with the plane-wave basis based on the density functional theory, as implemented in the Vienna ab initio simulation package [22]. The electron and core interactions were included by using the frozen-core all-electron projector augmented wave (PAW) method [23]. The exchange correlation function was treated by the generalized gradient approximation (GGA) proposed by PERDEW, BURKE and ERNZERHOF (PBE) [24]. The plane-wave basis set cut-off was set as 420 eV for all cases. The special points sampling integration over the Brillouin zone was employed by using the Monkhorst-Pack scheme [25] with a grid of 0.035 ?^-1. Convergence of the total energy with different number of k points and the plane-wave cut-off energy has been tested. The tolerances for geometry optimization were set as the difference in total energy within 1×10^-6 meV/atom. The elastic constants were determined by applying a set of given homogeneous deformation with a finite value and calculating the resulting stress with respect to optimizing the internal atomic freedoms, as implemented by MILMAN and WARREN [26]. Atoms were allowed to relax until Hellman–Feynman forces were less than 0.001 eV/? and the maximum strain value was 0.2%. The bulk modulus, shear modulus, elastic modulus, and Poisson ratio were thus derived from the Voigt-Reuss- Hill approximation [27].

3 Results and discussion

3.1 Crystal structure parameters

Almost all known transition metal semi-borides crystallize in a body centered tetragonal (Al₂Cu-type, Z=4) structure (D_4h¹⁸) with space group I4/mcm [21]. Hence, for Ti₂B, there are four formula units (f. u.) in the conventional tetragonal cell (Fig. 1(a)), in which the B and Ti atoms occupy the 4a (0, 0, 0) and 6h (1/6, 2/3, 0) positions, respectively. There exists an ambiguity regarding the crystal structure of TiB. WYCKOFF [28] reported TiB in FeB structure, whereas PEARSON [29] and LANDOLT-B?RNSTEIN [30] suggested NaCl and ZrS structure, respectively. However, recent investigations [31] have confirmed the FeB configuration. In our calculations, we have taken the orthorhombic FeB structure with the unit cell containing four f. u.      (Fig. 1(b)). TiB₂ typically crystallizes in the well-known AlB₂-type structure (P6/mmm, Z=1) with Ti and B atoms sitting at the origin and (1/3, 2/3, 1/2) sites (Fig. 1(c)), in which the coplanar graphite-like B layers are present alternatively with the close-packed Ti sheets.

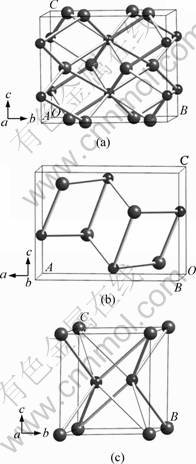
Fig. 1 Crystal structure of Ti₂B (a), TiB (b) and TiB₂ (c)) (Large and small spheres represent Ti and B atoms, respectively; a, b, c, A, B and C represent directions of crystal cells)

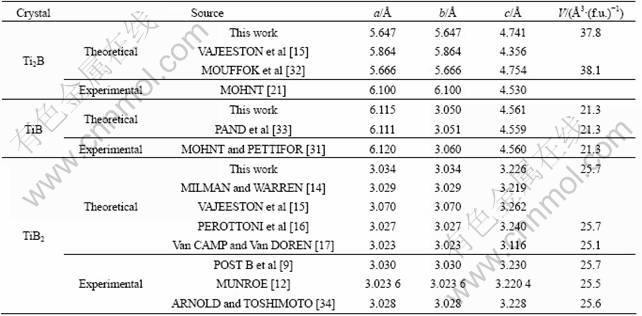
For each compound, the crystal structure was fully optimized with respect to the total energy to determine the lattice parameters: a, b, and c. The calculated lattice constants are given in Table 1, together with the available experimental data and previous theoretical values for comparison [9, 12, 14-17, 21, 31-34]. As seen from Table 1, agreement between the results of the present calculations and experimental data is very good: the deviations between the experimental and theoretical values for TiB and TiB₂ are all less than 1%. For tetragonal Ti₂B, the calculated lattice parameter a/c is 5.647/4.741, which is in excellent agreement with those previous theoretical calculations. However, compared with the experimental results [21], the highest disagreement in lattice constant a (7%) is obtained for Ti₂B. Here we shall emphasize that the transitional metal borides with metal-deficient or boron-deficient compositions can be easily obtained in actual experiments [35]. In one word, the agreement of the structural to be published results confirms the accuracy and reliability of the computational procedure employed.

Table 1 Calculated equilibrium lattice parameters a, b, c, and volume V for Ti₂B, TiB, and TiB₂ compounds

3.2 Mechanical properties

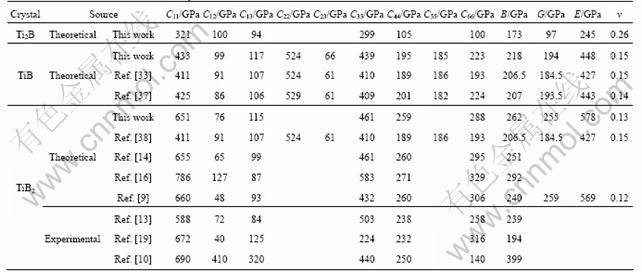
The accurate calculation of elasticity is essential for understanding the macroscopic mechanical properties of solid. Elasticity describes the response of a crystal under external strain and provides key information of the strength of the material, as characterized by elastic constants. To our knowledge, there is almost no experimental data about the elastic constants for Ti₂B and TiB except for TiB₂. We hope that our work could provide a useful reference for future study. The complete sets of zero-pressure single crystal elastic constants were calculated by using strain—stress method, as shown in Table 2. The elastic stability is a necessary condition for a stable crystal. A tetragonal crystal has to obey the following restrictions of its elastic constants [36]: C₁₁>0, C₃₃>0, C₄₄>0, C₆₆>0, (C₁₁-C₁₂)>0, (C₁₁+C₃₃-2C₁₃)>0 and 2(C₁₁+C₁₂)+C₃₃+4C₁₃>0. For a stable orthorhombic structure, C_ij has to satisfy the elastic stability criteria: C₁₁>0, C₂₂>0, C₃₃>0, C₄₄>0, C₅₅>0, C₆₆>0, C₁₁+C₂₂+C₃₃+ 2(C₁₂+C₁₃+C₂₃)>0, (C₁₁+C₂₂-2C₁₂)>0, (C₁₁+C₃₃-2C₁₃)>0 and (C₂₂+C₃₃-2C₂₃)>0. For the hexagonal structure with five independent elastic constants C₁₁, C₃₃, C₄₄, C₁₂ and C₁₃, they are C₃₃>0, C₄₄>0, C₁₁>|C₁₂|, (C₁₁+2C₁₂)C₃₃> 2C₁₃². In terms of the above conditions, the calculated elastic constants (Table 2) indicate that all these borides are mechanically stable. Our calculated elastic constants for TiB₂ are consistent with experimental and previous theoretical results [10-11, 13-14, 16, 19, 33, 37-38]. In addition, one should be aware that the values presented in Table 2 were obtained at T=0 K, and that temperature effects generally reduce the elastic constants. Therefore, we expect the experimental data for Ti₂B and TiB at room temperature to be smaller than those listed here.

Using the calculated elastic constants C_ij, bulk modulus and shear modulus for the corresponding polycrystalline aggregate are thus determined by the Voig-Reuss-Hill approximation method [27]. Furthermore, the elastic modulus E and Poisson ratio v are obtained in the light of the following equations:

                               (1)

                               (2)

The calculated bulk modulus, shear modulus, elastic modulus and Poisson ratio are listed in Table 2. Clearly, the calculated results for TiB₂ agree well with corresponding experiment [11], supporting the accuracy and reliability of our elastic calculations. For TiB, the large bulk modulus (218 GPa) manifests its strong incompressibility besides TiB₂. As expected, all these borides have larger bulk modulus than their parent metal (120 GPa) due to the direction bonding introduced by the boron atoms in the lattice. Moreover, it can be seen that the bulk modulus increases from 173 GPa to 262 GPa with the increase of the boron content in three borides, which are mainly due to the fact that the atomic volume decreases with the increase in the boron content in these borides. Furthermore, as a better indicator of potential hardness for materials, shear modulus quantifies the resistance to the shear deformation. Compared with the well-known hard TiB₂, TiB has a relatively large shear modulus shown in Table 2, indicating that it is expected to withstand shear strain to a certain extent and may act as hard material. By contrast, Ti₂B possesses much lower shear modulus than TiB and TiB₂, resulting in low bond-bending force constants and consequently a low hardness.

Table 2 Calculated elastic constants C_ij, bulk modulus B, shear modulus G, elastic modulus E and Poisson ratio v for three borides

It is well known that microcracks are easily induced in the materials due to the significant elastic anisotropy. Therefore, it is important to calculate elastic anisotropy in order to improve its mechanical durability. In view of the high bulk and shear moduli of TiB and TiB₂, we here have calculated the bulk modulus B along the different crystallographic axes for these two compounds. The anisotropy of the bulk modulus along the a-axis and b-axis with respect to the c-axis are given by A_Ba=B_a/B_c and A_Bb=B_b/B_c, where B_a, B_b, and B_c are the bulk modulus along different crystal axes, defined as B_i=idP/di, i=a, b, and c. Note that a value of 1.0 indicates elastic isotropy and any deviation from 1.0 represents elastic anisotropy. Using the relations mentioned above, the calculated parameters about elastic anisotropy together with the available experimental data are shown in Table 3. From our calculations, it is clear that both compounds are all elastic anisotropic. For TiB, it is interesting to note that the directional bulk modulus along the b-axis is larger than that along the a-axis or c-axis, which is consistent with the predicted elastic constants along different axes (see Table 2). Compared with TiB, TiB₂ is more anisotropic characterized by larger anisotropy of the bulk modulus A_Ba and A_Bb, which are also in agreement with experimental values [11].

As a fundamental parameter, Debye temperature closely relates to many physical properties of solids, such as specific heat, dynamic properties, and melting temperature [39]. At low temperature, it can be calculated from the elastic constants using the average sound velocity v_m, by the following equation:

                   (3)

where h is Planck’s constant; k is Boltzmann’s constant; N_A is Avogadro’s number; n is the number of atoms per formula unit; M is the molecular mass per formula unit; ρ is the density. The average sound velocity v_m is given by

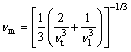                      (4)

where v_t and v_l are the transverse and longitudinal elastic wave velocities of the polycrystalline materials, respectively, and are given by Navier’s equation [40]. The calculated longitudinal, transverse and average elastic velocities, and Debye temperatures for three titanium borides are listed in Table 4. The calculated Debye temperature for TiB₂ is higher than that of Ti₂B or TiB, which agrees well with the experimental results [11, 41].

3.3 Electronic properties

To understand the mechanical properties of these borides on a fundamental level, the site projected and total electronic densities of states (DOS) of three titanium borides were calculated at zero pressure, as plotted in Fig. 2. It can be seen that all these compounds possess finite DOS at the Fermi level. Hence, these borides exhibit clear metallic behavior in their crystalline state. Moreover, the major orbital occupancy near Fermi level stems is predominated by the Ti-3d electrons, which are the principal cause for their metallicity. In Fig. 2, the DOS of Ti-3d and B-2p are energetically degenerated from the bottom of valence band to the Fermi level, indicating the covalent hybridization between the Ti and B atoms in these compounds, especially for TiB₂. It is earlier proposed that the lower DOS at the Fermi level often characterizes a more stable structure [42-43]. Among three borides, TiB₂ possesses the lowest DOS on the Fermi level, indicating its highest stability. Moreover, the decrease in the total DOS at the Fermi level is accompanied with the appearance of the pseudo gap around the Fermi level (Fig. 2(c)), which is helpful to increase the stability of TiB₂ and the strength of the covalent of the chemical bond between the Ti and B atoms. Since the coincidence between the pseudogap and the Fermi level in the TiB₂ is due to the band-filling effect and depends only on the electron number, it must be also noted that the presence of the Fermi level near the minimum of the DOS histogram indicates that the bonding states are occupied when all the antibonding ones are empty. So TiB₂ has better cohesively than Ti₂B and TiB. This is confirmed through the large bulk modulus of TiB₂ compared with Ti₂B and TiB.

Table 3 Calculated directional bulk modulus B_a, B_b, B_c, anisotropy factors A_Ba, and A_Bb of TiB and TiB₂

Table 4 Longitudinal, transverse, average elastic wave velocities (v_l, v_t and v_m), and Debye temperature Θ_D at theoretical equilibrium volume

Fig. 2 Calculated total and partial state density of Ti₂B (a), TiB (b) and TiB₂ (c)

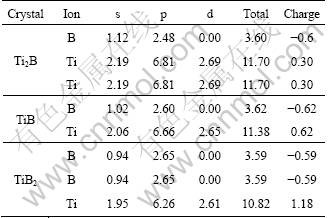
In order to understand the changes of the DOS on the Fermi level, we calculated the charge transfer situation between Ti and B atoms of Ti₂B, TiB and TiB₂ by the Mulliken atomic population analysis and tabulated them in Table 5. In Table 5, Ti atoms of TiB₂ have the largest charge values among the three titanium borides. The large charge transfering from Ti to B atoms of TiB₂ mainly comes from more electrons of Ti-3d orbital of TiB₂ taking part in the covalent bonding between Ti and B atoms or transferring from Ti and B atoms, which can be seen from the smallest Mulliken charge value (2.61). Consequently, the more Ti-3d electrons of TiB₂ become the bonding states than Ti₂B and TiB, which is accompanied with the larger decrease of Ti-3d states on the Fermi level. In addition, we found a charge transferring from Ti to B atom for all these borides, implying an ionic contribution to Ti—B bonding.    We thus conclude that the chemical bonding in these titanium borides is a complex mixture of covalent, ionic and metallic characters. Such a conclusion was also found in other transition metal borides [15, 44-45].

Table 5 Calculated atomic population of three titanium borides

4 Conclusions

1) Our calculated lattice parameters are in good agreement with the experimental data and previous theoretical values for these titanium borides. The calculated elastic constants indicate that all these borides are mechanically stable at ambient pressure.

2) The larger bulk modulus of these borides increase successively from Ti₂B to TiB₂ compared with parent metal Ti, which may be due to direction bonding introduced by the boron atoms in the lattice and the strong covalent Ti-B bonds. Additionally, TiB and TiB₂ show different degrees of elastic anisotropy. Debye temperatures calculated by elastic constants are 648 K for Ti₂B, 967.7 K for TiB, and 1 204.5 K for TiB₂.

3) According to the electronic density of states and Mulliken atomic population analysis, we thus conclude that the chemical bonding in these titanium borides is a complex mixture of covalent, ionic, and metallic characters

References

[1] LUNDSTORM T, RUNDQVIST S. Borides, silicides and phosphides [M]. London: Methuen, 1965.

[2] Serebriakova T I, Neronov V A, Peshev P D. High-temperature borides [M]. Moscow: Metallurgy, 1991. (in Russian)

[3] Basu B, Raju G B, Suri A K. Processing and properties of monolithic TiB₂ based materials [J]. Int Mater Rev, 2006, 51(6): 352-374.

[4] Tian D C, Wang X B. Electronic structure and equation of state of TiB₂ [J]. J Phys: Condens Matter, 1992, 4(45): 8765-8772.

[5] Atri R R, Ravichandran K S, Jha S K. Elastic properties of in-situ processed Ti-TiB composites measured by impulse excitation of vibration [J]. Mater Sci Eng A, 1999, 271(1-2): 150-159.

[6] Mitterer C, Losbichler P, Hofer F, Warbichler P, PGibson N, Gissler W. Nanocrystalline hard coatings within the quasi-binary system TiN-TiB₂ [J]. Vacuum, 1998, 50(3-4): 313-318.

[7] Mishra S K, Rupa P K P, Pathak L C. Surface and nanoindentation studies on nanocrystalline titanium diboride thin film deposited by magnetron sputtering [J]. Thin Solid Films, 2007, 515(17): 6884-6889.

[8] Kartal G, Timur S, Urgen M, Erdemir A. Electrochemical boriding of titanium for improved mechanical properties [J]. Surf Coat Technol, 2010, 204(23): 3935-3939.

[9] Post B, WGlaser F, Moskowitz D. Transition metal diborides [J]. Acta Metall, 1954, 2(1): 20-25.

[10] Gilman J J, Roberts B W. Elastic constants of TiC and TiB₂ [J]. J Appl Phys, 1961, 32(7): 1405.

[11] Spoor P S, Maynard J D, Pan M J, Green D J, Hellmann J R, Tanaka T. Elastic constants and crystal anisotropy of titanium diboride [J]. Appl Phys Lett, 1997, 70(15): 1959-1961.

[12] Munroe R G. Material properties of titanium diboride [J]. J Res Natl Inst Stand Technol, 2000, 105(5): 709-720.

[13] Manghnani M H, Fisher E S, Li F Y, Grady D E. Elastic moduli of TiB₂ [J]. Ceram Trans, 1993, 38(4): 771-785.

[14] Milman V, Warren M C. Elastic properties of TiB₂ and MgB₂ [J]. J Phys: Condens Matter, 2001, 13(24): 5585-5595.

[15] Vajeeston P, Ravindran P, Ravi C, Asokamani R. Electronic structure, bonding, and ground-state properties of AlB₂-type transition-metal diborides [J]. Phys Rev B, 2001, 63(4): 045115.

[16] Perottoni C A, Pereira A S, Jornada J A H da. Periodic Hartree-Fock linear combination of crystalline orbitals calculation of the structure, equation of state and elastic properties of titanium diboride [J]. J Phys: Condens Matter, 2000, 12(32): 7205-7222.

[17] Campa P E V, Dorena V E V. Ground state properties of titaniumdiboride [J]. High Pressure Research, 1995, 13(6): 335-341.

[18] Peng F, Fu H Z, Cheng X L. First-principles calculations of thermodynamic properties of TiB₂ at high pressure [J]. Physica B, 2007, 400(1-2): 83-87.

[19] Wright S. Estimation of single-crystal elastic constants from textured polycrystal measurements [J]. J Appl Crystallogr, 1994, 27(5): 794-801.

[20] Feng H B, Zhou Y, Jia D C, Meng Q C, Rao J C. Growth mechanism of in situ TiB whiskers in spark plasma sintered TiB/Ti metal matrix composites [J]. Crystal Growth & Design, 2006, 6(7): 1626-1630.

[21] Mohn P. The calculated electronic and magnetic properties of the tetragonal transition-metal semi-borides [J]. J Phys C: Solid State Phys, 1988, 21(15): 2841-2851.

[22] Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Phys Rev B, 1999, 59(3): 1758-1775.

[23] Bl?uml P E. Projector augmented-wave method [J]. Phys Rev B, 1994, 50(24): 17953-17979.

[24] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple [J]. Phys Rev Lett, 1996, 77(18): 3865-3868.

[25] Monkhorst H J, Pack J D. Special points for Brillouin-zone integrations [J]. Phys Rev B, 1976, 13(12): 5188-5192.

[26] Milman V, Warren M C. Elasticity of hexagonal BeO [J]. J Phys: Condens Matter, 2001, 13(2): 241-251.

[27] Hill R. On discontinuous plastic states, with special reference to localized necking in thin sheets [J]. J Mech Phys Solids, 1952, 1(1): 19-30.

[28] Wyckoff W G. Crystal structures [M]. New York: Wiley, 1963.

[29] Pearson W P. Handbook of lattice spacings and structures of metals and alloys [M]. New York: Pergamon, 1967.

[30] Landolt-B?rnstein. Numerical data and functional relationships in science and technology [M]. Berlin: Springer, 1971.

[31] Mohn P, Pettifor D G. The calculated electronic and structural properties of the transition-metal monoborides [J]. J Phys C: Solid State Phys, 1988, 21(15): 2829-2839.

[32] Mouffok B, Feraoun H, Aourag H. Electronic structure of some mono-, semi-titanium boride and diboride [J]. Mater Lett, 2006, 60(12): 1433-1436.

[33] Panda K B, Chandran K S R. First principles determination of elastic constants and chemical bonding of titanium boride (TiB) on the basis of density functional theory [J]. Acta Mater, 2006: 541641-541657.

[34] Arnold H S, Toshimoto K. Nuclear magnetic resonance in transition-metal diborides [J]. J Chem Phys, 1963, 38(4): 865-872.

[35] Hao X F, Xu Y H, Wu Z J, Zhou D F, Liu X J, Cao X Q. Low-compressibility and hard materials ReB₂ and WB₂: Prediction from first-principles study [J]. Phys Rev B, 2006, 74(22): 224112.

[36] Wu Z J, Zhao E J, Xiang H P, Hao X F, Liu X J, Meng J. Crystal structures and elastic properties of superhard IrN₂ and IrN₃ from first principles [J]. Phys Rev B, 2007, 76(5): 054115.

[37] YAO Qiang, XING Hui, MENG Li-jun, SUN Jian. Theoretical calculation of elastic properties of TiB₂ and TiB [J]. Chinese Journal of Nonferrous Metals, 2007, 17(8): 1297-1301. (in Chinese)

[38] Panda. K B, Chandran K S R. Determination of elastic constants of titanium diboride (TiB₂) from first principles using FLAPW implementation of the density functional theory [J]. Comput Mater Sci, 2006, 35(2): 134-150.

[39] Ravindran P, Fast L, Korzhavyi P A, Johansson B, Wills J, Eriksson O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi₂ [J]. J Appl Phys, 1998, 84(9): 4891-4904.

[40] Schreiber E, Anderson O L, Soga N. Elastic constants and their measurements [M]. New York: McGraw-Hill, 1973.

[41] Ledbetter H, Tanaka T. Elastic-stiffness coefficients of titanium diboride [J]. J Res Nat Inst Stand Technol, 2009, 114(6): 333-339.

[42] Xu J H, Freeman A. Phase stability and electronic structure of ScAl₃ and ZrAl₃ and of Sc-stabilized cubic ZrAl₃ precipitates [J]. Phys Rev B, 1990, 41: 12553-12561.

[43] Xu J H, Oguchi T, Freeman A J. Crystal structure, phase stability, and magnetism in Ni₃V [J]. Phys Rev B, 1987, 35: 6940-6943.

[44] Gou H Y, Hou L, Zhang J W, Li H, Sun G F, Gao F M. First-principles study of low compressibility osmium borides [J]. Appl Phys Lett, 2006, 88(22): 221904.

[45] Chiodo S, Gotsis H J, Russo N, Sicilia E. OsB₂ and RuB₂, ultra-incompressible, hard materials: First-principles electronic structure calculations [J]. Chem Phys Lett, 2006, 425(4-6): 311-314.

钛硼化物的结构、力学和电子性质的第一性原理研究

闫海燕¹，魏 群²，常少梅³，郭 平⁴

1. 宝鸡文理学院 化学化工系，宝鸡 721013；

2. 西安电子科技大学 物理系，西安 710071；

3. 宝鸡文理学院 物理系，宝鸡 721007；

4. 西北大学 物理系，西安 710069

摘  要：采用基于密度泛函理论的第一性原理计算方法研究了过渡族金属钛硼化物(Ti₂B, TiB和TiB₂)的晶体参数、力学性能和电子性质。晶格参数的计算结果与实验值以及其它理论计算值吻合得很好。弹性常数的计算结果表明，这3种硼化物在常压下都是力学稳定的。与金属钛相比(120 GPa)，3种硼化物的体弹模量都很大且随着硼含量的增加而增加，这可能是由金属晶格中引入的硼原子与钛原子之间形成定向共价键引起的。除TiB₂外，TiB具有较大的体弹模量和剪切模量，可以视作为一种具有良好抗压性质的硬质材料。此外，对这几种硼化物的弹性各向异性性质和德拜温度也进行了讨论。电子态密度和原子电荷布居分析表明，这3种硼化物的化学键成分同时包含了共价、离子和金属成分。

关键词：钛硼化物；第一性原理计算；力学性质；态密度；Mulliken原子布居分析

(Edited by YANG Hua)

Foundation item: Project (2010JK404) supported by the Education Committee Natural Science Foundation of Shaanxi Province, China; Projects (ZK0918, ZK0915) supported by the Baoji University of Arts and Sciences Key Research, China

Corresponding author: YAN Hai-yan; Tel: +86-917-3566589; E-mail: hyyan1102@163.com; WEI Qun; Tel: +86-917-3364258; E-mail: weiaqun@tom.com

DOI: 10.1016/S1003-6326(11)60906-0