J. Cent. South Univ. (2012) 19: 2016-2021
DOI: 10.1007/s11771-012-1239-3![]()
Coupling model for assessing anti-seepage behavior of curtain under dam foundation
PENG Peng (彭鹏)1, 2, SHAN Zhi-gang(单治钢)1, DONG Yu-fan(董育烦)1
1. Hydro China Huadong Engineering Corporation, Hangzhou 310000, China;
2. State Key Laboratory of Water Resources and Hydropower Engineering Science
(Wuhan University), Wuhan 430072, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract:
The seepage under a dam foundation is mainly controlled by the performance of the curtain. Its anti-seepage behavior may be weakened by the long term physic-chemical actions from groundwater. According to seepage hydraulics and geochemistry theory, a coupling model for assessing the behavior of the curtain under a dam foundation is set up, which consists of seepage module, solute transport module, geochemistry module and curtain erosion module, solved by FEM. A case study was carried out. The result shows that the curtain efficiency is weakened all the time. Aqueous calcium from the curtain is always in dissolution during the stress period for simulation, which leads to the increasing amount in groundwater reaching 846.35-865.312 g/m3. Within the domain, reaction extent differs in different parts of the curtain. The dissolution of Ca(OH)2 accounts to 877.884 g/m3 near the bottom and is much higher than that of the other parts. The erosion is much more serious near the bottom of the curtain than the other parts, which is the same to the upstream and downstream. Calcium dissolution is mainly controlled by hydraulic condition and dispersion, and it varies in a non-linear way within the domain.
Key words:
curtain; dam foundation; seepage; calcium ion leaching; coupling model;
1 Introduction
Seepage under a dam foundation is caused by high hydraulic pressure after impounding. As the curtain integrity and its anti-seepage efficiency are the critical processes that govern the seepage process, it is usually constructed to reduce the seepage or leakage. Coupled to the variations of seepage pressure and hydrochemistry, the dissolution of calcium ions from cementation zone is taken away by the fluids, which represents that a curtain is eroded. This results in increasing material porosity, and consequently increasing permeability, and decreasing mechanical properties. Therefore, the curtain efficiency is affected greatly by the flow and chemical fields [1].
In recent years, much of the present knowledge about curtain efficiency has been provided. WU and WANG [2] and GU and ZHANG [3] analyzed dam and its curtain working state through the groundwater regime under foundation. Finite element method simulating the unsteady-state flow was used to understand the curtain efficiency by FU and JIN [4]. As a consequence of water-rock interaction, water quality analysis around a dam foundation is a helpful investigative means to evaluate the anti-seepage performance of the curtain [5-7]. A model coupled of seepage field and stress field was built up by SHEN et al [8] to describe the real system. CHEN et al [9] believed that the interaction of seepage and stress couldn’t be ignored; it would result in the increase of stress level and seepage velocity, especially near the water-tight core. The results showed that the earth dam stability would be reduced when the coupling effect of seepage field and stress field was considered. DING and SHENG [10] made the seepage-stress coupled analyses on the dam foundation of 3# section in left bank power station, and the influence of pore water pressure on the stress and displacement of dam and foundation was discussed. The distribution characteristics of seepage field, stress and deformation of rock foundation were studied when different anti-seepage and drainage systems were adopted. SHENG et al [11] and CHAI and LI [12] set up different equations coupled of seepage and stress fields separately to analyze the groundwater macroscopic dynamics under dam foundation and to determine the hydro-geology parameters. The coupled analysis of dam site showed that the seepage field of coupled analysis is different from that of uncoupled analysis. The water pressure in the roof of underground opening of coupled analysis is larger than that of uncoupled analysis and the rock mass around the dam has great permeability with the magnitude 10-5-10-4m/s. But, it is hard to find the coupling model for assessing the anti-seepage behavior of curtain under dam foundation, especially in which the chemical reaction was considered.
In this work, a multi-physics model is set up, coupled of seepage field, a chemical reactive and mass transport field, which is solved by FEM. The simulation integrates a description of curtain efficiency variation which is of visualization in FEMLAB.
2 Multi-physics coupling model
2.1 Assumptions
Assumptions are given as follows:
1) The saturated porous medium is homogeneous and continuous, in which the flow is governed by Darcy’s law;
2) Hydraulic conductivity is only a spatial function, not variable with time;
3) The aquifer does not contribute other components to the variation of solute;
4) The amount of ions in groundwater varies only due to the dissolution/precipitation reactions, which could be modeled by using thermodynamic and kinetic laws.
2.2 Multi-physics model
A multi-physics model, used to simulate water-rock-dam interaction around a dam site, consists of four modules: seepage module [13], chemical reaction module [14-16], solute transport module [17-20] and curtain erosion module [21]. As the chemical module, it is given as
![]() (1a)
(1a)
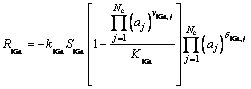 (1b)
(1b)
![]() (1c)
(1c)
![]() (1d)
(1d)
 (1e)
(1e)
![]() (1f)
(1f)
![]() (1g)
(1g)
![]() (1h)
(1h)
where C is the total concentration, while Ci is the special one from the mineral dissolution concerned; Xq is the change of concentration related to thermodynamics; Nc is the amount of species; ai is the activity of component i; Fi is the stoichiometric coefficient of species i; vij is the stoichiometric coefficient of species j in reaction i; A and B are constants; I is ionic concentration; bi is constant; ηi is activity of species i in groundwater; Tj is amount of species j; RKin is a temporal variation related to kinetics; S is the specific surface area of mineral; Ki is the equilibrium constant of reaction.
As for curtain erosion module, it can be described as
![]() (2)
(2)
where θ is the curtain porosity; Csolid is the ionic concentration concerned; D(C) is the ionic dispersion.
2.3 Methodology
In numerical simulation, there are full and separate couplings in multi-physics models. Usually, the former is called as a direct coupling method and the latter as an indirect coupling one. Direct coupling method can be used in solving nonlinear and interactive equations in fully coupled models, and therefore it can solve all equations at the same time. However, indirect coupling method is often used in solving separately coupled models and it must solve equations in a certain order. Therefore, the field of seepage module is calculated and taken as the boundary conditions of the field of the next module. As a result, it can reduce calculation time and improve efficiency. In this work, the latter method is adopted to solve multi-physics models. The main steps could be described as follows [22-25]:
1) At first, the field of seepage module is calculated. When a constant water head is given, the water head distribution (seepage discharge) can be calculated at first in ?t.
2) Based on water head distribution (seepage discharge), dissolved (precipitated) quantity of minerals in ?t is calculated by adopting chemical module. In chemical module, both kinetic and thermodynamic models are used to achieve local equilibrium.
3) The calcium ion concentration can be calculated by adding its increasing quantity which comes from the dissolution of minerals to the original water. And then, the results are applied to the solution transport module and calculated by FEM. Therefore, distribution of calcium ion concentration under a dam foundation can be obtained.
4) Based on the amount of the calcium ion in the groundwater under a dam foundation, the amount of the calcium ion in curtain under a dam foundation in ?t can be calculated by adopting curtain erosion module.
5) Steps 2-4 are repeated until a high precision is achieved.
FEMLAB is a powerful interactive software for modeling many kinds of scientific and engineering problems based on partial differential equations (PDEs). The package provides a number of application modules such as fluid mechanics, electromagnetics, structural mechanics and secondary development [26]. The chemical reaction module can be developed by adding some thermodynamic and kinetic equations in this work.
3 A case study
3.1 General description
The dam, with the width of 60 m in foundation and 13 sections, is located on a series of limestone and dolomite. The level is 135 m in upstream, while 15 m in downstream. And the curtain constructed at upstream is 100 m deep and 5 m wide to reduce leakage. It is of vital importance in groundwater variation. And it is harmful to the curtain of dam because of great water pressure.
3.2 Simulation
The model includes four steps: meshing, seepage simulation, chemical reactive transport simulation and leaching simulation of the curtain. Tables 1, 2 and 3 give some input data for the model. Table 1 shows some chemical compositions of the reservoir water and groundwater from drainage hole. Table 2 shows some hydro geological parameters of modeling area. Table 3 shows some geo-chemical reactions among water-rock- curtain system and their thermodynamic parameters in the area.
At first, the domain is divided into triangular mesh elements of different sizes according to the boundary conditions, reaching 16 258 mesh partitions. As the head of the upstream and downstream is constant, the steady-state seepage is simulated for calculating the hydraulic head and fluid velocity within the domain.
Secondly, chemical reactive transport module is used for describing the curtain behavior. It takes 10 d as a time-step and the total time is 7 200 d. Figures 1-5 show some results at different stress time from simulation.
Table 1 Chemical compositions (mg/L) and pH value of water
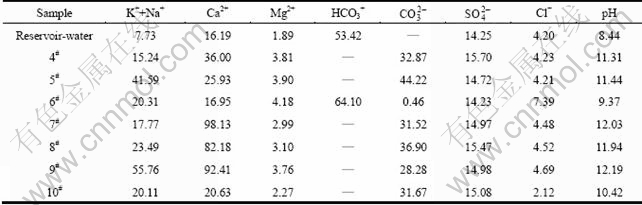
Table 2 Hydro geological parameters of modeling area
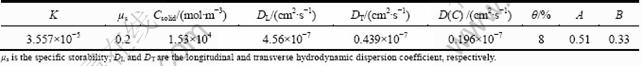
Table 3 Geo-chemical reactions among water-rock-curtain system and their thermodynamic parameters in area
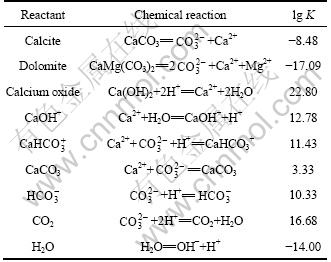
3.3 Results and discussion
From Figs. 1-5, following discussion could be presented.
1) Within the domain, reaction extent differs in different parts of the curtain. The dissolution of Ca(OH)2 accounts to 877.884 g/m3 near the bottom and is much higher than that of other parts (Fig. 1 and Fig. 2). Obviously, these losses will cause porosity increasing and permeability of the curtain, which again will affect the anti-seepage performance of the curtain and its durability.
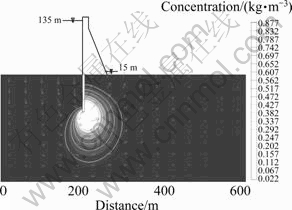
Fig. 1 Distribution of Ca2+ concentration after 360 d in cross section 6
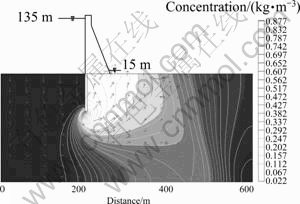
Fig. 2 Distribution of Ca2+ concentration after 7 200 d in cross section 6
2) Aqueous calcium has been always in dissolution during the stress period for simulation, which leads to the increasing amount in groundwater reaching 846.35-865.312 g /m3 (Fig. 3 and Fig. 4).
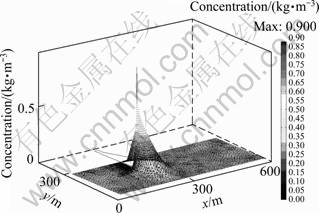
Fig. 3 Distribution of Ca2+ concentration after 360 d along vertical direction in domain
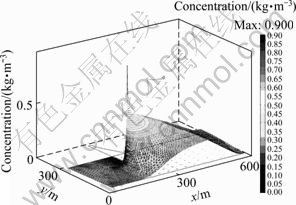
Fig. 4 Distribution of Ca2+ concentration after 7 200 d along vertical direction in domain
3) The erosion is much more serious near the bottom of the curtain than other parts, which is the same to the upstream and downstream (Fig. 5). This might be related to the flow velocity and hydraulic pressure.
4) Calcium dissolution mainly takes place at the bottom of the curtain and transports in three sub-zones. The first is behind the curtain and toward the downstream by 45° with the highest concentration of 600-700 g/m3. The second is at the curtain bottom and toward the upstream by 45° with the concentration of 400-600 g/m3. And the last is behind the curtain and toward downstream by 135° with the concentration of 200-400 g/m3. The former two are the consequences of both hydraulic condition and dispersion, while the last one is caused by the dispersion of calcium concentration near the upstream.
5) Water-rock-curtain interaction is thermo- dynamic; however, at the bottom of the curtain, the long-term reaction is more aggressive. It can be deduced that the anti-seepage efficiency of the curtain is weakened with time.
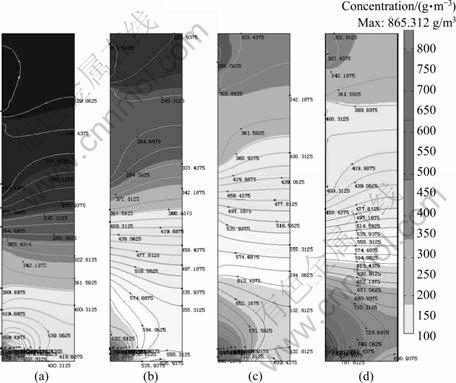
Fig. 5 Distribution of Ca2+ concentration within curtain at different time: (a) 1 800 d; (b) 3 600 d; (c) 5 400 d; (d) 7 200 d
To analyze the variation of concentration field and velocity with time, Figs. 6 and 7 show the calcium concentration that is 5 m and 45 m away from the curtain bottom, respectively.
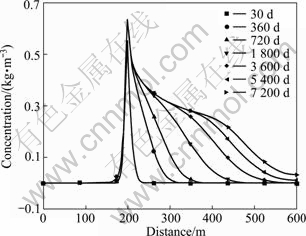
Fig. 6 Distribution of Ca2+ concentration at 5 m from curtain after different times
Figure 6 shows the variation of Ca2+ concentration with time at the curtain bottom along the river. It reaches the highest value at the bottom of the curtain, 0.558 kg/m3 at 30 d and 0.637 kg/m3 at 7 200 d. It increases much more slowly far away from the local, and the slowest rate is at the upstream according to the hydraulic condition.
Figure 7 shows the variation of Ca2+ concentration with time at the location 45 m away from the curtain bottom along the river. It has the similar distribution to Fig. 6. However, the concentration range at 5 m away from the bottom is much larger between that at 30 d and 7 200 d, with the highest value of 0.318 kg/m3, and the lowest value of 0.025 kg/m3. Within the domain, the concentration increases slowly, especially near the curtain. It varies in a non-linear way.
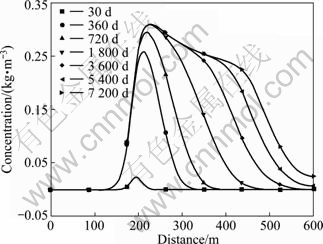
Fig. 7 Distribution of calcium ion concentration at 45 m from curtain after different times
4 Conclusions
1) A coupling model is set up for simulating water-rock-curtain interaction, which can be used to describe the evolution of both a curtain and groundwater in components, which represents the physico-chemical damage of the curtain in both spatial and temporal scales.
2) The curtain anti-seepage efficiency is weakened all the time. Aqueous calcium from the curtain is always in dissolution during the stress period for simulation, which leads to the increasing amount in groundwater reaching 846.35-865.312 g/m3. The erosion is much more serious near the bottom of the curtain than the other parts.
3) Calcium dissolution mainly takes place at the bottom of the curtain and transports mainly in three sub-zones. The first is behind the curtain and toward the downstream by 45° with the highest concentration. The second is at the curtain bottom and toward the upstream by 45°. And the last is behind the curtain and toward downstream by 135°. The former two are the consequences of both hydraulic condition and dispersion, while the last one is caused by the dispersion of calcium concentration near upstream. Within the domain, the concentration increases slowly, especially near the curtain, and it varies in a non-linear way.
4) The reaction between fluid and solid phases may lead to variation of curtain permeability, porosity and calcium leaching quantity, which represents the weakening trend of the anti-seepage of curtain.
References
[1] OUYANG Chang-yun. Technical problems about Geheyan Project's seepage proof curtain [J]. Yangtze River, 1995, 6(5): 10-15. (in Chinese)
[2] WU Zhong-ru, WANG Zhan-rui. Dynamic monitoring model of space displacement field of concrete dam [C]// International Symposium on Monitoring Technology of Dam Safety. 1992: 215-224.
[3] GU Chong-shi, ZHANG Qian-fei. Research on seepage monitoring model of earth-rock dam [J]. Journal of Hydrodynamics, 2003, 16(1): 62-74.
[4] FU Jun-feng, JIN Sheng. A study on unsteady seepage flow though dam [J]. Journal of Hydrodynamics, 2009, 21(5): 434-442.
[5] YANG Guang-zhong, PENG Han-xing, MA Xiao-hui. Evaluation of seepage field of grouting curtain in Dan Jiangkou dam [J]. Journal of Hydroelectric Engineering, 2000(4): 33-39. (in Chinese)
[6] SONG Han-zhou, ZHOU Jian, WANG Feng-bo. Study of groundwater quality evolution around dam-site and its significance [J]. Journal of Hydroelectric Engineering, 2004, 23(3): 74-78. (in Chinese).
[7] TONG Hai-tao, SONG Han-zhou. Reliability analysis of stochastic modeling for water-rock interaction [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(12): 2010-2014. (in Chinese)
[8] SHEN Zhen-zhong, CHEN Xiao-hu, XU Li-qun. Coupled analysis of stress-seepage interaction for gravity dam by element-free method [J]. Rock and Soil Mechanics, 2008, 29(11): 74-78. (in Chinese)
[9] CHEN Xiao-ping, QIAN Ping-yi, LIANG Zhi-song. Coupled analysis of stress-seepage interaction for dam [J]. Rock and Soil Mechanics, 2008, 29(11): 74-78. (in Chinese)
[10] DING Xiu-li, SHENG Qian. Seepage-stress coupled analysis on the dam foundation of 3# section in left bank power station of the three gorges project [J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(s): 1001-1005. (in Chinese)
[11] SHENG Jin-chang, SU Bao-yu, ZHAO Jian. Coupled stress and fluid analysis and concerned application in Xiluodu hydropower station [J]. Rock and Soil Mechanics, 2000, 21(4): 410-415. (in Chinese)
[12] CHAI Jun-rui, LI Shou-yi. Analysis of coupled seepage and stress fields in rock mass around the Daliushu dam [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(s1): 2322-2325. (in Chinese)
[13] CHAN D Y C, HUGHES B D. Transient flow around the boreholes [J]. Transport in Porous Media, 2003, 10(1): 137-152.
[14] ALIM TURSUN. Numeric hydro-geo-chemical modeling of dam foundation ageing [D]. Nanjing: Hohai University, 2005. (in Chinese)
[15] BABU D K, BANSAL P P. Analytical solution to Cl- flow through porous media [J]. Transport in Porous Media, 2005, 23(7): 17-19.
[16] ZHAO Ming-deng, LI Tai-ru, HUAI Wen-xin. Finite proximate method for convection-diffusion equation [J]. Journal of Hydrodynamics, 2008, 20(1): 47-53.
[17] ZHANG Qian-fei, LAN Shou-qi, XU Yong-fu. A new numerical method for groundwater flow and solution transport using velocity field [J]. Journal of Hydrodynamics, 2008, 20(3): 356-364.
[18] tan ye-fei, ZHOU Zhi-fang. Simulation of solute transport in a parallel single fracture with LBM/MMP mixed method [J]. Journal of Hydrodynamics, 2008, 20(3): 365-372.
[19] zhou yan-zhang, ZHOU Zhi-fang. Simulation of thermal transport in aquifer: A GWHP system in Chengdu, China [J]. Journal of Hydrodynamics, 2009, 21(5): 647-657.
[20] WANG Song-qing, ZHANG Xu. Variation characteristics of aquifer parameters induced by groundwater source heat pump operation under variable flow [J]. Journal of Central South University of Technology, 2011, 18(4): 1272-1277.
[21] GERARD B, PIJAUDIER CABOT G, LA BORDERIE C. Coupled diffusion-damage modeling and the implications on failure due to strain localization [J]. International Journal of Solids and Structures, 1998, 35(30): 4107-4120.
[22] COMSOL A B. Multi-physics version 3.4. User’s guide and reference guide [M]. Stockholm, 2009: 165-172.
[23] WANG Jin-guo, ZHOU Zhi-fang, JIN Zhong-qing. Coupled method of method of BEM-FAM for simulation of groundwater thermal transport [J]. Journal of Hydrodynamics, 2001, 9(5): 71-76.
[24] LI Min, DIAO Nai-ren, FANG Zhao-hong. Analysis of seepage flow in a confined aquifer with a standing column well [J]. Journal of Hydrodynamics, 2007, 19(1): 84-91.
[25] WANG Guo-jian, CHENG Tong-jin, FAN Ming, REN Chun, CHEN Wei-jun. Laboratory simulation of vertical hydrocarbon micro seepage [J]. Acta Geological Sinica, 2011, 85(1): 223-232.
[26] SHENG Jin-chang. Fully coupled thermo-hydro-mechanical model of saturated porous media and numerical modeling [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(s1): 3028-3033. (in Chinese)
(Edited by YANG Bing)
Foundation item: Project(50139030) supported by the National Natural Science Foundation of China; Project(501072) supported by the Scientific Research Foundation for the Returned Overseas Scholars of the Ministry of Education of China
Received date: 2011-04-13; Accepted date: 2011-10-08
Corresponding author: PENG Peng, PhD; Tel: +86-571-56738493; E-mail: hhu_pengpeng@126.com
Abstract: The seepage under a dam foundation is mainly controlled by the performance of the curtain. Its anti-seepage behavior may be weakened by the long term physic-chemical actions from groundwater. According to seepage hydraulics and geochemistry theory, a coupling model for assessing the behavior of the curtain under a dam foundation is set up, which consists of seepage module, solute transport module, geochemistry module and curtain erosion module, solved by FEM. A case study was carried out. The result shows that the curtain efficiency is weakened all the time. Aqueous calcium from the curtain is always in dissolution during the stress period for simulation, which leads to the increasing amount in groundwater reaching 846.35-865.312 g/m3. Within the domain, reaction extent differs in different parts of the curtain. The dissolution of Ca(OH)2 accounts to 877.884 g/m3 near the bottom and is much higher than that of the other parts. The erosion is much more serious near the bottom of the curtain than the other parts, which is the same to the upstream and downstream. Calcium dissolution is mainly controlled by hydraulic condition and dispersion, and it varies in a non-linear way within the domain.


