J. Cent. South Univ. Technol. (2011) 18: 1750-1756

DOI: 10.1007/s11771-011-0898-9

A mechanical system to predict wet grip potential of pavements

CHEN Xian-hua(陈先华)¹, B. Steinauer², A. Ueckermann²

1. School of Transportation, Southeast University, Nanjing 210096, China;

2. Institute of Road and Traffic Engineering, RWTH-Aachen University, D52074, German

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Key words:

wet grip; rubber tyre rim; penetration depth; friction coefficient; dynamic model；

1 Introduction

Skid resistance is an essential component of traffic safety as it is critical in maintaining vehicle control and reducing the stopping distance in emergency braking situations especially under wet conditions. The pavement surface must provide an adequate level of friction at the tire-to-pavement interface for safe operation of vehicles under normal weather conditions. The comprehension of physical mechanisms involved during rubber tires interacting with rough road surfaces is a decisive step for the prediction and the improvement of tyre wet grip performance and the friction potential of a pavement as a function of its texture. To achieve these goals, it is critical to develop a tire-road friction model which is able to predict the friction coefficient of a pavement based on its measured texture.

Friction is the tangential reaction force between two surfaces in contact. Physically, these reaction forces are the results of many different mechanisms like adhesion, hysteresis, cohesion and viscous friction, which depend on contact geometry and topology, properties of the bulk and surface materials of the bodies, displacement and relative velocity of the bodies and presence of lubrication [1-2]. The behavior of friction has been extensively examined. The experiments have been performed under idealized conditions with clean surfaces and stationary conditions, e.g., constant velocity. Lately, the interest in friction dynamics has increased. In recent years, much progress has been made in the physical understanding and modeling of the rubber frictions at rough substrate, e.g. road surface [3-6] A. Le Gal, X. Yang and M. Klüppel, J. Chem. Phys.. This provides a fundamental physical background for understanding the dynamic contact of tires with road tracks and the friction behaviors during cornering and braking [6]. Two mechanisms are usually known to primarily contribute to the rubber friction during sliding at a rigid surface, namely an adhesive component and a hysteresis component [3-4, 6-7]. The adhesion component arises from molecular interactions between two surfaces during the sliding process, and the distribution of contact patches is constantly renewed within the contact area, inducing a cyclic formation and breakage of molecular bonds between polymer chains and surface asperities associated with dissipative effects. The contribution of adhesion to friction dominates for a very smooth substrate and can be strongly reduced due to the interfacial lubricating [8-9]. For rough surfaces, on the other hand, the adhesive contribution to friction will be much smaller because of small contact area [8-9]. The hysteresis component referred to as the deformation contribution is resulted from the energy lost through the macroscopic dynamic deformation process of a certain volume of rubber induced by the surface roughness [8]. The level of hysteresis friction is promoted with increasing surface roughness and appears to be a determining factor for tyre grip performance under wet conditions. It is reasonable that adhesive forces are neglected under wet conditions and wet grip of pavement can totally be allocated to hysteretic effects within the rubber generated by the asperities of the road surface intruding into the tire tread.

The aim of this work is to develop a tool for predicting the wet grip potential of pavements based on the measured texture. Firstly, the hysteresis friction theory proposed by Persson has been overviewed. Since the hysteresis friction is closely related to the viscoelastic spectrum of rubber tyre rim, the complex dynamic modulus of tire rubber has been proved to be frequency-, strain- and temperature-dependent. Secondly, a generalized master procedure related to the time- temperature superposition principle and Payne effect with generalized Maxwell elements for rubbers tyre tread is presented. Thirdly, the integrated models with 2D numerical multi-body system consisting of interconnected masses, dampers and springs for wet grip are presented with a time step integration scheme to solve the numerical equations. Finally, the discussion on the output of the tool and the validation has been made.

2 PERSSON’s theory on hysteresis friction

The hysteresis friction of rubber is caused by the energy dissipation due to the internal material damping during the process of deformation. The deformation itself occurs during the sliding of a rubber element across the micro-scaled asperities of a rough surface. In recent 40 years, many approaches to hysteresis friction on rough substrates were developed based on static or dynamic contact mechanics with fractal/spectral methods. PERSSON [8, 10] has reviewed the contact mechanical models proposed by HERTZ, GREENWOOD- WILLIAMSON, ARCHARD, BUSH, GIBSON and THOMAS et al. He points out that those models have two drawbacks as they neglect the interaction between the different contact regions and the contact mechanics theories can only be applied as long as A<<>₀. A general theory of the hysteretic contribution to rubber friction has been developed by PERSSON [6, 8] to overcome these drawbacks, together with a simple rheological model of the complex elastic modulus. The theory is a continuation of the early studies of GROSCH, taking into account that the sliding friction of rubber has the same temperature dependence as that of the complex elastic modulus. PERSSON’s theory of rubber friction also differs from the theory of KL?PPEL and HEINRICH [5, 11] in that it is fully three-dimensional, and the deformations of the rubber in response to the surface roughness are taken into account on all relevant length scales, in contrast to Refs.[5,11], where this effect was only taken into account in some average way.

According to PERSSON [6, 8], the contribution to rubber friction from the viscoelastic deformation of the rubber surface by the substrate asperities depends only on the complex frequency-dependent viscoelastic modulus of the rubber and on the substrate surface roughness power spectrum. The roughness power spectrum governs rubber friction on rough substrates, e.g., friction of tyres on a road surfaces, and in?uences other phenomena of technological importance, e.g., the roughness-induced leaking of sealings. Let h(X) be the substrate height profile measured from the average surface plane defined so that áh(0)?=0, where á…? stands for ensemble averaging or averaging over the total surface. The surface roughness power spectrum is defined as Eq.(1), which can be easily obtained from the surface height profile. The height profile can be measured routinely on all relevant length scales using different methods such as atomic force microscopy (AFM), and optical methods.

                             (1)

In considering surfaces on which the statistical properties are translationally invariant and isotropic, such as self-affine pavement surface, the surface roughness power spectrum C(q) only depends on the magnitude of the wave q.

The main contribution to rubber friction when a rubber block slides on a rough substrate, such as in the case of a tyre on a road surface, is the viscoelastic energy dissipation in the surface region of the rubber as a result of the pulsating forces acting on the rubber surface from the substrate asperities. Neglecting the flash temperature, the friction coefficient is given by a sum over different length scales:

      (2)

where

whereis the complex viscoelastic

modulus of rubber, σ₀ is the averaged pressure in the nominal contact area A₀,  is the Poisson ratio which is equal to 0.5 for rubber, and v is the sliding velocity. The theory takes into account of the substrate roughness in the range of  where  is the smallest relevant wave of order 2π/L, L is the diameter of the nominal contact area, and  is the large wave cut-off which may be related to road contamination, or may be an intrinsic property of the tyre rubber [8].

3 Modelling of rubber

Since the hysteresis friction is closely related to the viscoelastic spectrum of rubber, it is common to use the simple three-parameter Maxwell constitutive model [6,8] or Rouse model [5] for rubber. For realistic rubber tyre rim, however, these simple models are not capable of representing viscoelastic behavior over a range of temperatures and strain levels. The three-parameter model is easily generalized to 2N+1 parameter model, as shown in Fig.1, or to what is sometimes called the Zener model.

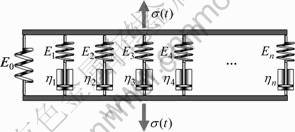
Fig.1 Schematic of one “elementary” rubber element

The constants E_i and η_i (i=0, 1, 2, …, n) represent various spring and damper elements of the model and the constant E₀ is referred to as the long term or equilibrium modulus. According to this generalized 2N+1 parameter model, the dynamic modulus of rubber can be expressed by the PRONY series [12] as

         (1)

where E(jω) is the magnitude of the complex modulus with real and imaginary components, called the storage and loss moduli, respectively; τ_i=η_i/E_i is the characteristic period of the various viscous elements of the model; ω is the circular frequency. Identification of these discrete spectral values in Eq.(3) has been conducted based on experimental results tested in DIK of German, with a method described by EMRI and TSCHOEGL [13-15], as shown in Fig.2.

Implicitly material properties E(jω) is dependent on temperature and strain rate. The temperature-frequency equivalency can be transformed by WLF equation according to WILLIAM et al [16]. The strain-dependence called Payne-effect [17-18] manifests the fact that an increase in amplitudes leads to a decrease in storage modulus and a maximum in loss modulus. It can be proximated by a phenomenological quantitive model according to KRAUS [19]. In the frequency domain, the superposition principle relates to properties at temperatures and frequencies according to the relationships as

                                                  (4)

where  is the shift factor at temperature T.

where T_r is the reference temperature, and C₁ and C₂ are empirical constants.

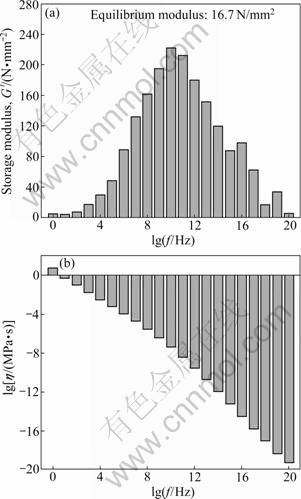
Fig.2 Discrete spectra with 21 pairs of prony coefficient identified: (a) Storage moduli; (b) Loss moduli

With the determined shift factors and incorporating with KRAUS [19] model, we can formulate strain-dependent spring and damper constants, and are now able to identify and describe the frequency-, strain- and temperature-dependent behaviour of rubber element in Fig.1, as

                                    (5)

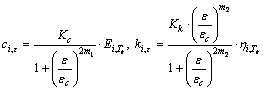        (6)

where c and k represent spring and damp constants respectively. T and ε mean temperature and strain dependent sub-indices, respectively.

4 Integrated model for wet grip

4.1 Physical model

The physical model for wet grip is built up by a number of interconnected Zener elements with coupling spring, as shown in Fig.3. Figure 3(a) presents one elementary rubber element (ERE), and it has got an additional attached mass, accounting for the mass of the tire tread; three of the EREs are connected to one by coupling springs; the EREs in turn are connected to the tire rim by rigid joints. The unloaded length of each of EREs is 10 mm, which is about the height of the tire tread. The distance between them is 3.3 μm. Input parameter of the system is the exciting texture profile w(t) and output parameter is the deformed rubber shape h(t) as well as the “inner” displacement z_i(t) of each of EREs.

4.2 System equations

The differential equation system is illustrated in Fig.4. This equation system must be solved for any given time step. Only the first two elementary rubber elements can be illustrated (from a total number of up to 30 000). On the left of the equation is the first derivative of the solution vector, which contains (top-down) the “inner” displacements z₁, …, z_n, the (outer) displacement h and velocity of the first two EREs. On the right-hand side of the equation we find the excitation vector, w_i^*(t), mainly influenced by the texture shape w(t), which is moved horizontally underneath the rubber system with given sliding velocity. Besides, the mass of the ERE and the stiffness of the road surface determines w_i^*(t) are shown in Eq.(7):

                                                     (7)

To the left of the excitation vector, w_i^*(t), we find the solution vector and the huge sparse matrix at the left built up by elements containing the masses, spring and damper constants, where c_ij  is the spring constant of spring i in ERE j (i=0, 1, …, N), c_kj is the spring constant of coupling spring of ERE j, k_ij is the damper constant of damper i in ERE j (i=0, 1, …, N), m is the mass of ERE, Sc_ij is the abbreviation for c_0j+2c_kj+Sc_ij+c_asp, and c_asp is the spring constant of road surface.

The matrix elements mentioned above, except for the mass of course, are frequency-, strain- and temperature-dependent.

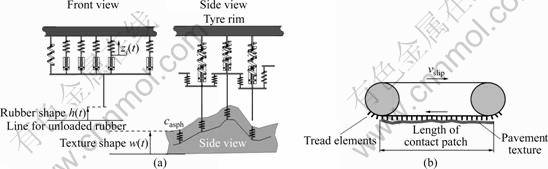
Fig.3 Rubber friction model (friction prediction): (a) Interconnected elementary rubber elements; (b) Physical model

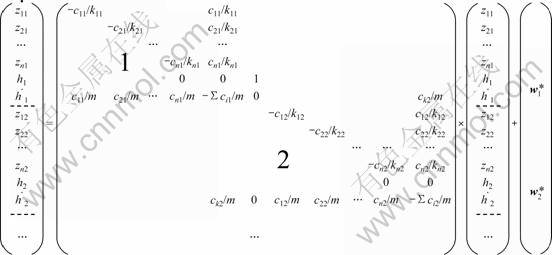
Fig.4 Differential equation system of rubber model

4.3 Structure of program

The tool structure consists of a main program in which the mechanical system and initial conditions are defined and subprograms in which the time step analysis is performed, i.e. assembling the sparse matrix, defining the ODE system, calculating the dissipated energy, temperature rise and consequent friction coefficient at the specified time and location. There are two basic modules to which the above mentioned structure is applied: the penetration depth module, and the friction module, as shown in Fig.5. Both modules use the same program structure and algorithm. The only difference is the kind of movement. The penetration depth module calculates the vertical movement of the rubber tread into the texture, whereas the friction module calculates the horizontal (sliding) movement of the rubber tread along the road.

5 Validation of system

5.1 Penetration depth

The penetration depth module determines the amount of the rubber tread that penetrates into the surface texture of the road. This information is crucial for the rubber model because the penetration depth determines the resulting texture profile that the tire faces and thus the excitation function of the rubber. Figure 6 shows the results of penetration depths for different sliding velocities. It can be clearly seen that the penetration depth decreases with increasing the speed of the car, which is obvious with increasing the speed, i.e. exciting frequency that the rubber becomes stiffer and thus penetrates the road surface to a lower extent.

Figure 6 shows the results in a context with penetration depths found in Ref.[20]. Based on the measured texture profiles of three different asphalt surfaces, one coarse stone matrix asphalt SMA0/11, one coarse asphalt concrete AB 0/11S and 8 normal asphalt concrete surfaces AB 0/8S, the appropriate penetration depths were calculated for different wheel velocities. It can be seen that the results found with the penetration model fits well with the results found in literature. Figure 7 finally shows the deformed shape of the rubber at the end of the penetration process. In the enlargement, one can see how the rubber “flows” around the asperities of the texture. It can be seen that the model is able to describe the deformations of rubber in macro- and micro-scale and the penetration depths (depending on the vertical loads on the rubber) are realistic and conform with penetration depths of real tires. It should be noted that the calculations on such a high resolution of 3.3 μm to produce results like ones shown in Fig.7 are very time-consuming.

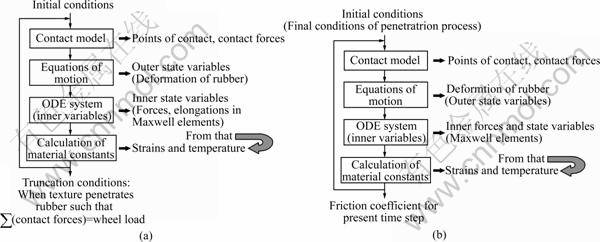
Fig.5 Penetration depth module (a) and friction module (b) of program

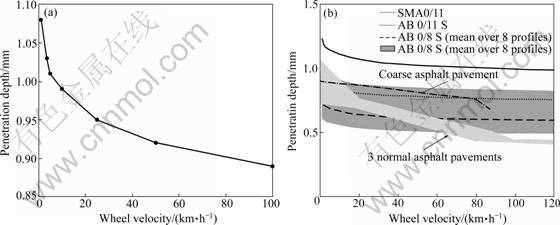
Fig.6 Penetration depths for varying speed: (a) Output of programme; (b) Results in Ref.[20]

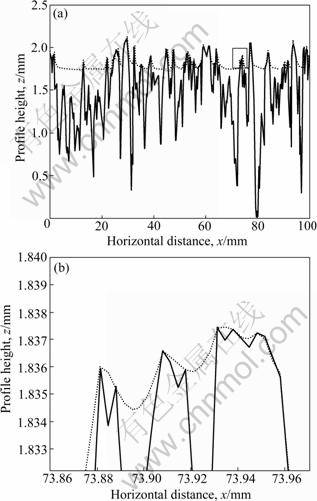
Fig.7 Rubber deformation due to vertical penetration into texture

5.2 Friction coefficient

Once the maximum penetration depth is determined, the friction during horizontal sliding can be calculated, i.e. the final conditions of the penetration process are the initial conditions of the horizontal sliding process, from which the coefficient of friction shall be calculated. Figure 8 shows a result of friction calculation using 24 time steps. After about 10 time steps, the output of the model reaches an equilibrium phase and the hysteresis friction coefficient converges at 0.5-0.9 with a mean value of 0.69, as shown in Fig.8(a). The mean value is very close to the measured results of 0.56 by dynamic friction tester of ISAC, RWTH-AACHEN. Figure 8(b) shows the simulated friction coefficient at equilibrium phase as a function of sliding velocity. The friction coefficient results are promising compared with the previous numerical results [10-11], which demonstrates that the tool can be used for wet grip prediction.

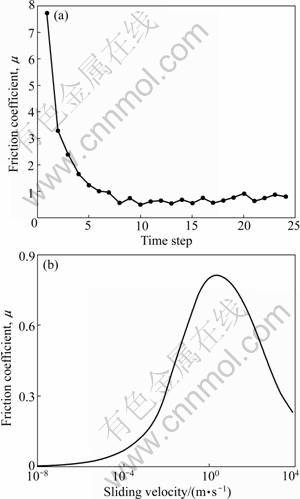
Fig.8 Convergence test (a) and simulated hysteresis friction coefficient (b) results

6 Conclusions

1) A mechanical system for predicting the wet grip potential of asphalt pavement has been systematically presented using an extended rubber material model by a time step integration scheme.

2) This analytical approach is transferred to a 2D numerical multi-body system consisting of interconnected masses, coupling spring and elementary rubber element of a generalized Maxwell model of rubber tyre tread. The advantage of the method described above is the approximation of the real physical hysteretic friction process and its description in time domain.

3) The system consists of two basic modules with the same program structure and algorithm, considering the frequency-, temperature-, and strain-dependency behaviors of the complex dynamic modulus of rubber element.

4) Input of the system is the measured texture profile of pavement and the outputs are penetration depth and friction coefficient. The dependence of penetration depth and friction coefficient on the velocity is simulated and validated.

5) This system can give reasonable prediction of wet grip potential of pavements.

References

[1] PERSSON B N J. Sliding friction: Physical principles and applications [M]. Germany: Springer, 2000.

[2] WEN Shi-zhu, HUANG Ping. The principle of tribology [M]. 3rd Ed. Beijing: Tsinghua University Press, 2009: 1-20. (in Chinese)

[3] MOORE D F. The friction and lubrication of elastomers [M]. Oxford: Pergamon Press, 1972: 20-24.

[4] GROSCH K A. The rolling resistance, wear and traction properties of tread compounds [J]. Rubber Chem Technol, 1996, 69: 495-568.

[5] HEINRICH G, KL?PPEL M, VILGIS T A. Evaluation of self-affine surfaces and their implication for frictional dynamics as illustrated with a Rouse material [J]. Computational and Theoretical Polymer Science, 2000, 10: 53-61.

[6] PERSSON B N J. Theory of rubber friction and contact mechanics [J]. J Chem Phy, 2001, 115(8): 3840-3861.

[7] SCHRAMM E J. Friction of elastomers on rough surfaces and description of wet braking performance of passenger car tires [D]. Regensburg und Hannover: University of Regensburg, 2002. (in German)

[8] PERSSON B N J, ALBOHR O, TARTAGLINO U, VOLOKITIN A I, TOSATTI E. On the nature of surface roughness with application to contact mechnics, sealing, rubber friction and adhesion [J]. J Phys: Condens Matter, 2005, 17: R1-R62.

[9] PAN Xiao-dong. Wet sliding friction of elastomer compounds on a rough surface under varied lubrication conditions [J], Wear, 2007, 262: 707-717.

[10] PERSSON B N J. Contact mechanics for randomly rough surfaces [J]. Surface Science Reports, 2006, 61(4): 201-227.

[11] HEINRICH G, KL?PPEL M. Rubber friction, tread deformation and tire traction [J]. Wear, 2008, 265: 1052-1060.

[12] PRONY R. Essai experimental et analytique etc [J]. J Ecole Polytech, 1795, 1(2): 24-76.

[13] EMRI I, TSCHOEGL N W. Generating line spectra from experimental responses: Part I. Relaxation modulus and creep compliance [J]. Rheol Acta, 1993, 32: 311-321.

[14] TSCHOEGL N W, EMRI I. Generating line spectra from experimental responses: Part II. Storage and loss functions [J]. Rheol Acta, 1993, 32: 322-327.

[15] EMRI I, TSCHOEGL N W. Generating line spectra from experimental responses: Part IV. Application to experimental data [J]. Rheol Acta, 1994, 33: 60-70.

[16] WILLIAMS M L, LANDEL R F, FERRY J D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids [J]. J Am Chem Soc, 1955, 77: 3701-3707.

[17] PAYNE A R. The dynamic properties of carbon black-loaded natural rubber vulcanizates: Part I [J]. J Appl Polym Sci, 1962, 6(19): 57-53.

[18] PAYNE A R. The dynamic properties of carbon black-loaded natural rubber vulcanizates: Part II [J]. J Appl Polym Sci,1963, 6(21): 368-372.

[19] KRAUS G. Mechanical losses in carbon black filled rubbers [J]. J Appl Poly Sci, 1984, 39: 75-92.

[20] BACHMANN T. Investigation of the use of tire sensors in the passenger car tire [D]. Darmstadt: TU Darmstadt, 1999. (in German)

(Edited by YANG Bing)

Foundation item: Project(FP6-PL-0506437) supported by European Commission; Project(50908053) supported by the National Natural Science Foundation of China

Received date: 2010-08-16; Accepted date: 2011-01-15

Corresponding author: CHEN Xian-hua, Associate Professor, PhD; Tel: +86-25-83790522; E-mail: chenxh@seu.edu.cn