
A method for calculating damage evolution in adiabatic shear band of titanium alloy
WANG Xue-bin(王学滨)
College of Mechanics and Engineering, Liaoning Technical University, Fuxin 123000, China
Received 27 August 2008; accepted 25 March 2009
Abstract:
A method for calculating the evolution of the local damage variable at the adiabatic shear band (ASB) center was proposed. In the present method, the JOHNSON-COOK model and the nonlocal theory were adopted, and the damage variable formula applicable for the bilinear (linearly elastic and strain-softening) constitutive relation was further generalized to consider the plastic deformation occurring in the strain-hardening stage. Aiming at Ti-6Al-4V, the effect of strain rate on the evolution of the local damage variable at the ASB center was investigated. In addition, a parametric study was carried out, including the effects of strain-hardening exponent, strain rate sensitive coefficient, thermal-softening exponent, static shear strength, strain-hardening modulus, shear elastic modulus, work to heat conversion factor, melting temperature and initial temperature. The damage extent at the ASB center in the radial collapse experiment was assessed. It is found that at higher strain rates the damage in the ASB becomes more serious at the same average plastic shear strain of the ASB.
Key words:
adiabatic shear band; damage variable; titanium alloy; nonlocal theory; JOHNSON-COOK model; strain-hardening; strain rate;
1 Introduction
Many experimental observations show that voids are generated in adiabatic shear bands(ASBs) of titanium alloys and other materials[1-6]. The nucleation, growth and coalescence of voids will form macrocracks. In this process, the load-carrying capacity of the material will be greatly weakened. So it will be controlled by the weakest parts of the material, i.e., ASBs. The further development of voids and/or microcracks in ASBs will result in the gradual damage in ASBs. Apparently, the more serious the damage extent in an ASB is, the weaker the ASB is. Thus, the lower load-carrying capacity of the material will be expected. Beyond the occurrence of the ASB, it is difficult to assess the damage extent in the ASB. As is known, no internal length parameter is included in the classical elastoplastic theory. Therefore, the thickness of the ASB and the nonuniform distribution of mechanical and physical parameters, such as strain, deformation, temperature rise and damage variable, cannot be accurately predicted.
After introducing gradient-dependent plasticity (a special case of the nonlocal theory) into the JOHNSON- COOK (J-C) model, WANG[7-11] investigated the distribution of the local strain, deformation and the temperature rise in ASBs of Ti-6Al-4V alloy and steels, the phase transformation condition and the thickness of the transformed ASB.
By using the nonlocal theory, the problem of damage localization of geomaterials was studied by WANG et al[12]. It was found that the local damage variable distribution in the tensile localization band in uniaxial tension was highly nonuniform. At the center of the band, the local damage variable reached its maximum, while at the two boundaries of the band it decreased to zero. By using the bilinear (linearly elastic and strain- softening) constitutive relation identical to that in Ref.[12], WANG[13] investigated the damage variable distribution in the shear band in a rock specimen in uniaxial compression and that in the tensile localization band in a three-point bending beam, respectively. On dynamic shear loading, WANG[14] investigated the local damage variable distribution in the ASB propagation process. However, the bilinear constitutive relation was still adopted. Obviously, the simple bilinear constitutive relation is not completely applicable for Ti-6Al-4V alloy.
In this work, a method for calculating the evolution of the local damage variable at the ASB center was proposed. In the present method, the J-C model and nonlocal theory were adopted and the damage variable formula applicable for the bilinear constitutive relation was further generalized to consider the plastic deformation occurring in the strain-hardening stage. Aiming at Ti-6Al-4V, the effect of the strain rate on the evolution of the local damage variable at the ASB center was investigated. In addition, a parametric study was carried out. The most serious damage extent in the ASB in the radial collapse experiment was also assessed.
2 Analysis and discussion
2.1 Basic formulas
To calculate the evolution of the maximum damage variable in an ASB (Fig.1) with decreasing shear stress τ, the following equations (Eqs.(1-5)) will be used. Eq.(1) is the J-C model[7-11, 15]. Eq.(3) is the shear Hooke’s law. Eq.(5) demonstrates the distribution of the local damage variable D(y) in the ASB.
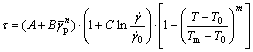 (1)
(1)
T=T0+![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
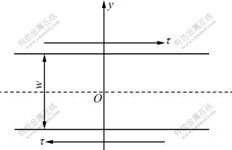
Fig.1 Narrow ASB in simple shear
where ![]() is the average plastic shear strain of the ASB;
is the average plastic shear strain of the ASB; ![]() is the reference shear strain rate;
is the reference shear strain rate; ![]() is the imposed shear strain rate; T0 is the initial temperature; Tm is the melting temperature; β is the work to heat conversion factor; cp is the heat capacity; ρ is the density; A, B, C, m, and n are the static shear strength, strain-hardening modulus, strain rate sensitive coefficient, thermal-softening exponent and strain-hardening exponent, respectively; γe is the elastic shear strain in the ASB; G is the shear elastic modulus; T is the average temperature in the ASB;
is the imposed shear strain rate; T0 is the initial temperature; Tm is the melting temperature; β is the work to heat conversion factor; cp is the heat capacity; ρ is the density; A, B, C, m, and n are the static shear strength, strain-hardening modulus, strain rate sensitive coefficient, thermal-softening exponent and strain-hardening exponent, respectively; γe is the elastic shear strain in the ASB; G is the shear elastic modulus; T is the average temperature in the ASB; ![]() (the elastic part of
(the elastic part of ![]() is γe and γe remains uniform distribution in the ASB) is the average shear strain of the ASB;
is γe and γe remains uniform distribution in the ASB) is the average shear strain of the ASB; ![]() is the critical plastic shear strain, i.e., the average plastic shear strain corresponding to the occurrence of the ASB (Fig.2); y is the coordinate whose original point O is set at the ASB center (Fig.1); and l is the internal length parameter, reflecting the heterogeneous extent of ductile metal materials (the lower the value of l is, the more homogenous the material is). l is related to the ASB thickness (w):
is the critical plastic shear strain, i.e., the average plastic shear strain corresponding to the occurrence of the ASB (Fig.2); y is the coordinate whose original point O is set at the ASB center (Fig.1); and l is the internal length parameter, reflecting the heterogeneous extent of ductile metal materials (the lower the value of l is, the more homogenous the material is). l is related to the ASB thickness (w):
w=2πl (6)
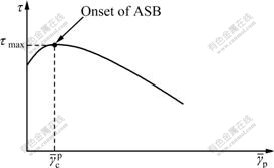
Fig.2 Relationship between shear stress and average plastic shear strain of ASB
2.2 Local damage variable in ASB
![]() and
and ![]() in Eq.(5) can be determined by using Eqs.(1)-(4).
in Eq.(5) can be determined by using Eqs.(1)-(4). ![]() corresponds to the peak shear stress τmax.
corresponds to the peak shear stress τmax.
As is known, Eqs.(1) and (2) are more complex. Therefore, the analytical solutions of ![]() and D(y) cannot be derived. It is found from Eq.(5) that D(±w/2)=0. This means that at the two boundaries of the ASB, no damage occurs. Damage only appears in the ASB. When y=0, D(y) reaches its maximum. This reflects that at the ASB center the damage extent is the most serious. The two special cases mentioned above are reasonable.
and D(y) cannot be derived. It is found from Eq.(5) that D(±w/2)=0. This means that at the two boundaries of the ASB, no damage occurs. Damage only appears in the ASB. When y=0, D(y) reaches its maximum. This reflects that at the ASB center the damage extent is the most serious. The two special cases mentioned above are reasonable.
Let the elastic shear strain corresponding to the occurrence of the ASB be ![]() (Fig.3).
(Fig.3). ![]() can be described by Hooke’s law:
can be described by Hooke’s law:
![]() (7)
(7)
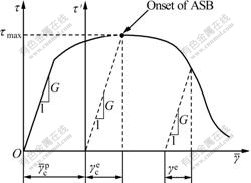
Fig.3 Relationship between shear stress and total shear strain of ASB
In the work, the occurrence of the ASB is believed to obey the maximum shear stress criterion. When the ASB is just initiated, we have τ=τmax, ![]() (
(![]() is the critical shear strain) and
is the critical shear strain) and ![]() . Thus, Eq.(5) can be written as
. Thus, Eq.(5) can be written as
![]() (8)
(8)
It is found from Eqs.(7) and (8) that D(y)=0. This means that when the ASB just appears, no damage occurs in any position of the ASB. This viewpoint is in agreement with the common knowledge.
When τ→0 in Eq.(5), we can find
![]() (9)
(9)
When y=0 in Eq.(9), we have D(0)→1. This means that a macroscopical fracture will take place along the center of the ASB. Similarly, when ![]() →∞ in Eq.(5) and y=0, we also have D(0)→1.
→∞ in Eq.(5) and y=0, we also have D(0)→1.
2.3 Nonlocal theory
As is known, in the elastic stage, no damage occurs in the material. Thus, using Eq.(3), we have
τ=Gγe (10)
The elastic stage is followed by the strain-hardening stage. In this stage, no damage appears until τ=τmax. When the condition is satisfied, the ASB occurs, followed by the strain-softening stage. In this stage, the thermal-softening effect dominates and overwhelms the effects of the strain-hardening and strain rate-hardening. In the strain-softening stage, the nucleation, growth and coalescence of voids and the initiation, propagation and combination of microcracks in the ASB cannot be neglected. Therefore, the damage in the ASB must be considered.
In the classical damage mechanics, in the strain- softening stage, the relationship between shear stress (τ) and total shear strain (γ) can be described by using Eq.(11) if the damage is taken into account:
τ=Gγ(1-D) (11)
where D is the damage variable. Eq.(11) cannot describe the distribution of the damage variable and the most serious damage extent at the ASB center. Therefore, new theories must be considered, such as the so-called nonlocal theory. Before the nonlocal theory is considered, Eq.(11) needs to be slightly modified to ensure that the maximum value of the local damage variable at the ASB center is one. Otherwise, it will be two. Herein, we modify Eq.(11) as
τ=![]() (12)
(12)
where ![]() is the average total shear strain in the ASB and
is the average total shear strain in the ASB and ![]() is the average damage variable in the ASB.
is the average damage variable in the ASB.
In order to consider interactions and interplay among microstructures (the microstructural effect) in the context of the classical damage theory, the variable ![]() in Eq.(12) needs to be seen as a nonlocal variable in the nonlocal damage theory. According to the nonlocal theory,
in Eq.(12) needs to be seen as a nonlocal variable in the nonlocal damage theory. According to the nonlocal theory, ![]() can be strictly derived as
can be strictly derived as
![]() (13)
(13)
Eq.(13) shows that the nonlocal damage variable ![]() is related to the internal length parameter l, the local damage variable D(y) and its second-order derivative dD2(y)/dy2. This means that the damage extent at a point of the material not only depends on the damage extent of itself, but also is influenced by the damage extent of its neighborhoods. The second-order derivative introduces spatial interactions[16] in Eq.(13).
is related to the internal length parameter l, the local damage variable D(y) and its second-order derivative dD2(y)/dy2. This means that the damage extent at a point of the material not only depends on the damage extent of itself, but also is influenced by the damage extent of its neighborhoods. The second-order derivative introduces spatial interactions[16] in Eq.(13).
The derivation of Eq.(13) includes three steps: weighting the local damage variable in the form of spatial averages, expending the local damage variable into a Tayor series and neglecting terms of order four and higher. In the first step, the weight function includes the internal length parameter, l, governing the distance at which spatial interactions among microstructures occur.
2.4 Derivation of local damage variable
Eq.(12) is applicable for the case that the material exhibits bilinear behavior in the linearly elastic and strain-softening stage. However, the measured shear stress—shear strain curves of titanium alloy specimens do not obey the bilinear assumption[5]. Beyond the linearly elastic stage, a wide plateau appears. In this stage, the shear stress firstly increases slowly until a peak shear stress is attained. This stage is called the strain-hardening stage. Then, beyond the peak stress, the shear stress decreases slowly. After that, the shear stress begins to decrease rapidly until the final fracture takes place. In the strain-hardening stage, no damage occurs although the shear strain progressively increases and is greater than zero (Figs.2 and 3). As a result, the critical plastic shear strain ![]() needs to be subtracted from the total shear strain
needs to be subtracted from the total shear strain ![]() . Thus, Eq.(12) is modified as
. Thus, Eq.(12) is modified as
![]() (14)
(14)
This modification is equivalent to moving the τ-axis to τ′-axis. The τ′—![]() curve can be still seen as two parts: the linearly elastic stage and the post-peak strain- softening stage.
curve can be still seen as two parts: the linearly elastic stage and the post-peak strain- softening stage.
We can obtain the expression for D(y), see Eq.(5), in terms of Eqs.(13) and (14) using the method in Refs.[12-14]. In the analytical process, three conditions need to be adopted: the symmetry of D(y) with respect to the coordinate y, the boundary condition and the assumption about the ASB thickness. The last condition results in Eq.(6).
Using Eq.(5), we can obtain the maximum local damage variable D(0) at the ASB center:
D(0)=![]() (15)
(15)
Using Eq.(3), we have
D(0)=![]() (16)
(16)
Using Eq.(4), we have
D(0)=![]() (17)
(17)
Eq.(15) shows that D(0) is dependent on three factors: the elastic shear strain ![]() in the ASB, the average plastic shear strain
in the ASB, the average plastic shear strain ![]() of the ASB and the critical plastic shear strain
of the ASB and the critical plastic shear strain ![]() (corresponding to the onset of the ASB).
(corresponding to the onset of the ASB).
It is noted that when the ASB is just initiated, we have ![]() However, after the ASB initiation,
However, after the ASB initiation, ![]() >γe<
>γe<![]() holds true.
holds true.
3 Example and parametric study
Fig.4 shows the effects of ![]() , n, C, m, A, B, G, β, Tm and T0 on τ—
, n, C, m, A, B, G, β, Tm and T0 on τ—![]() curve and D(0)—
curve and D(0)—![]() curve. Beyond the peak stress, the damage in the ASB begins to occur and D(0) will be greater than zero.
curve. Beyond the peak stress, the damage in the ASB begins to occur and D(0) will be greater than zero.
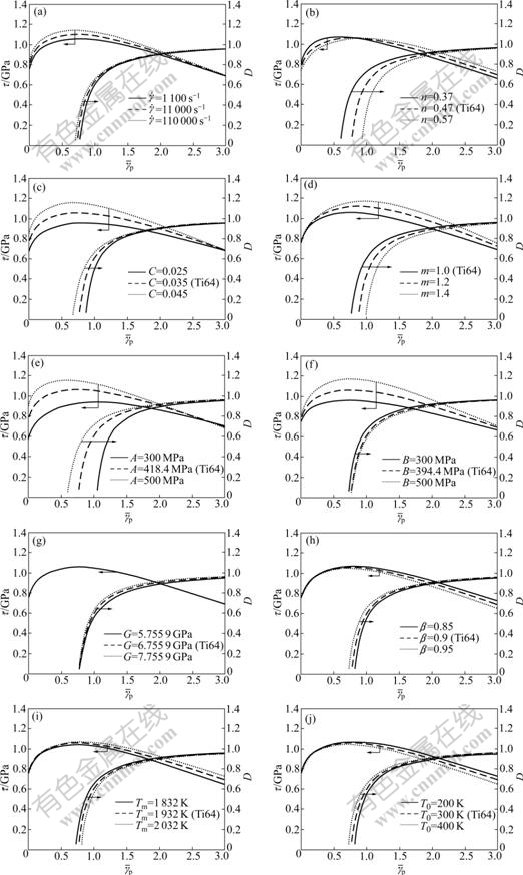
Fig.4 Effects of strain rate (a), strain-hardening exponent (b), strain rate sensitive coefficient (c), thermal-softening exponent (d), static shear strength (e), strain-hardening modulus (f), shear elastic modulus (g), work to heat conversion factor (h), melting temperature (i) and initial temperature (j) on evolution of maximum local damage variable in ASB
It is found from Fig.4 that D(0) increases with increasing ![]() or decreasing τ. The D(0)—
or decreasing τ. The D(0)—![]() curve exhibits the upward convex characteristic. The initial value of D(0) is zero, while the critical value is one.
curve exhibits the upward convex characteristic. The initial value of D(0) is zero, while the critical value is one.
It is noted that in Fig.4(a) the used parameters are identical to the values of Ti-6Al-4V alloy[3], namely, A=418.4 MPa, B=394.4 MPa, C=0.035, m=1.0, n=0.47, Tm=1 932 K, ρ=4 430 kg/m3, T0=300 K, ![]() =0.000 01 s-1, cp=564 J/(kg·K) and β=0.9. Fig.4(a) demonstrates the influence of
=0.000 01 s-1, cp=564 J/(kg·K) and β=0.9. Fig.4(a) demonstrates the influence of ![]() on τ—
on τ—![]() curve and D(0)—
curve and D(0)—![]() curve of Ti-6Al-4V. LIAO and DUFFY[5] performed dynamic torsional experiments to investigate the process of initiation and formation of ASBs in Ti-6Al-4V and the strain rate was in the range of 8 000- 13 000 s-1. In the present work, Fig.4(a) includes the results of the strain rate of 11 000 s-1. According to the measured shear stress—shear strain curve of the specimen TA-83[5], the adopted value of the shear elastic modulus is G=6.755 9 GPa.
curve of Ti-6Al-4V. LIAO and DUFFY[5] performed dynamic torsional experiments to investigate the process of initiation and formation of ASBs in Ti-6Al-4V and the strain rate was in the range of 8 000- 13 000 s-1. In the present work, Fig.4(a) includes the results of the strain rate of 11 000 s-1. According to the measured shear stress—shear strain curve of the specimen TA-83[5], the adopted value of the shear elastic modulus is G=6.755 9 GPa.
In Fig.4(b)-(j), ![]() =11 000 s-1. When the effects of a parameter are studied, the used other parameters are identical to those of Ti-6Al-4V[3].
=11 000 s-1. When the effects of a parameter are studied, the used other parameters are identical to those of Ti-6Al-4V[3].
Fig.4(a) shows that at higher strain rates, D(0) is higher at the same ![]() . This means that the damage extent in the ASB becomes more serious. It is obvious that the result is realistic. When
. This means that the damage extent in the ASB becomes more serious. It is obvious that the result is realistic. When ![]() is higher, the difference among the results at different strain rates becomes negligible.
is higher, the difference among the results at different strain rates becomes negligible.
It is found from Figs.4(b)-(j) that, D(0) is higher at lower n, m, B and Tm or higher C, A, G, β and T0 at the same ![]() , leading to more serious damage extent in the ASB.
, leading to more serious damage extent in the ASB.
Since the effects of ρ are opposite to those of cp and β, the effects of ρ and cp do not need to be presented.
4 Experimental verification
XUE et al[1] conducted the radial collapse experiment of a thick-walled cylinder of Ti-6Al-4V alloy under high-strain-rate deformation (about 104 s-1). They used the ASB edge length-to-thickness (δ/t) ratios to estimate the shear strains in ASBs. In Fig.5(b) in Ref.[1], the typical edge length δ was about 30 μm. A new measurement is conducted in the present work and it is found that the edge length is 28.8 μm, close to 30 μm. The typical thickness t of the ASB is 8 μm[1]. This gave a shear strain (expressed by ![]() in the present work) a value of about 4 [1]. If we select
in the present work) a value of about 4 [1]. If we select ![]() =104 s-1, G=6.755 9 GPa and the parameters of Ti-6Al-4V in Ref.[3] were used, the calculated maximum damage variable D(0) in the ASB is 0.978 3 when
=104 s-1, G=6.755 9 GPa and the parameters of Ti-6Al-4V in Ref.[3] were used, the calculated maximum damage variable D(0) in the ASB is 0.978 3 when ![]() =4, which is lower than 1. If δ=28.8 μm, then the assessed D(0) will be lower than 0.978 3. Indeed, no voids are observed at the center of the ASB in Figs.5(b)-(c) in Ref.[1]. Therefore, the present theoretical prediction is reasonable. Moreover, we can find that when
=4, which is lower than 1. If δ=28.8 μm, then the assessed D(0) will be lower than 0.978 3. Indeed, no voids are observed at the center of the ASB in Figs.5(b)-(c) in Ref.[1]. Therefore, the present theoretical prediction is reasonable. Moreover, we can find that when ![]() =13.106, D(0) reaches 1. This suggests that the voids have appeared at the ASB center. In addition, when
=13.106, D(0) reaches 1. This suggests that the voids have appeared at the ASB center. In addition, when ![]() =1.957, D(0)=0.9; when
=1.957, D(0)=0.9; when ![]() =5.183, D(0)=0.99; when
=5.183, D(0)=0.99; when ![]() =8.677, D(0)=0.999; when
=8.677, D(0)=0.999; when ![]() =11.550, D(0)=0.999 9.
=11.550, D(0)=0.999 9.
The assessed maximum shear strain in the ASB was over 200 with δ=1.67 mm[1]. Possibly, voids have been changed into a shear crack through a process of void nucleation, growth, elongation and rotation. While, the present theoretical result shows that voids appear when ![]() >13.106.
>13.106.
5 Conclusions
1) Three factors govern the evolution of the maximum damage extent in the ASB, that is, the elastic shear strain in the ASB, the average plastic shear strain of the ASB and the critical plastic shear strain (corresponding to the onset of the ASB). The former is related to Hooke’s law, while the latter two are described by the J-C model.
2) At the same average plastic shear strain of the ASB, the damage in the ASB becomes more serious when the strain rate, strain rate sensitive coefficient, static shear strength, shear elastic modulus, work to heat conversion factor and initial temperature increase or the strain-hardening exponent, thermal-softening exponent, strain-hardening modulus and melting temperature decrease.
References
[1] XUE Q, MEYERS M A, NESTERENKO V F. Self-organization of shear bands in titanium and Ti-6Al-4V alloy [J]. Acta Mater, 2002, 50(3): 575-596.
[2] ZHANG Xin-ming, LI Hui-jie, LI Hui-zhong, GAO Hui, GAO Zhi-guo, LIU Ying, LIU Bo. Dynamic property evaluation of aluminum alloy 2519 by split Hopkinson pressure bar [J]. Trans Nonferrous Met Soc China, 2008, 18(1): 1-5.
[3] DARIDON L, OUSSOUADDI O, AHZO S. Influence of the material constitutive models on the adiabatic shear band spacing: MTS, power law and Johnson-Cook models [J]. Int J Solids Struct, 2004, 41(11/12): 3109-3124.
[4] LEE D G, LEE S, LEE C S. Quasi-static and dynamic deformation behavior of Ti-6Al-4V alloy containing fine α2-Ti3Al precipitates [J]. Mater Sci Eng A, 2004, 366(1): 25-37.
[5] LIAO S C, DUFFY J. Adiabatic shear bands in a Ti-6Al-4V titanium alloy [J]. J Mech Phys Solids, 1998, 46(11): 2201-2231.
[6] ODESHI A G, AL-AMEERI S, MIRFAKHRAEI S, YAZDANI F, BASSIM M N. Deformation and failure mechanism in AISI 4340 steel under ballistic impact [J]. Theoretical and Applied Fracture Mechanics, 2006, 45(1): 18-24.
[7] WANG Xue-bin. Temperature distribution in adiabatic shear band for ductile metal based on Johnson-Cook and gradient plasticity models [J]. Trans Nonferrous Met Soc China, 2006, 16(2): 333-338.
[8] WANG Xue-bin. Effects of constitutive parameters on adiabatic shear localization for ductile metal based on Johnson-Cook and gradient plasticity models [J]. Trans Nonferrous Met Soc China, 2006, 16(6): 1362-1369.
[9] WANG X B. Effects of temperature and strain rate on the evolution of thickness of transformed adiabatic shear band [J]. Solid State Phenomena, 2008, 138: 385-392.
[10] WANG Xue-bin. Adiabatic shear localization for steels based on Johnson-Cook model and second- and fourth-order gradient plasticity models [J]. J Iron Steel Res Int, 2007, 14(5): 56-61.
[11] WANG Xue-bin. Quantitative calculation of local shear deformation in adiabatic shear band for Ti-6Al-4V [J]. Trans Nonferrous Met Soc China, 2007, 17(4): 698-704.
[12] WANG X B, YANG M, PAN Y S. Analysis of plastic strain localization, damage localization and energy dissipated localization for strain-softening heterogeneous material based on gradient- dependent plasticity [J]. Key Eng Mater, 2004, 274/276: 99-104.
[13] WANG Xue-bin. Local and global damages of quasi-brittle material in uniaxial compression based on gradient-dependent plasticity [J]. Key Eng Mater, 2005, 293/294: 719-726.
[14] WANG Xue-bin. Analysis of damage localization for ductile metal in the process of shear band propagation [J]. Trans Nonferrous Met Soc China, 2006, 16(1): 153-158.
[15] YANG Yang, ZENG Yi, WANG Bing-feng. Dynamic constitutive relationship of TC16 titanium alloy based on Johnson-Cook model [J]. The Chinese Journal of Nonferrous Metals, 2008, 18(3): 505-510. (in Chinese).
[16] PEERLINGS R H J, GEERS M G D, DE BORST R, BREKELMANS W A M. A critical comparison of nonlocal and gradient-enhanced softening continua [J]. Int J Solid Struct, 2001, 38(44/45): 7723-7746.
Foundation item: Project(20081102) supported by the Doctor Startup Foundation of Liaoning Province, China
Corresponding author: WANG Xue-bin; Tel: +86-418-3350924; E-mail: wxbbb@263.net
DOI: 10.1016/S1003-6326(08)60439-2


