平面光波导与阵列光纤耦合分析
郑 煜,段吉安
(中南大学 现代复杂装备设计与极端制造教育部重点实验室,湖南 长沙,410083)
摘 要:
摘 要:根据光波导理论,论述平面光波导与阵列光纤对准耦合原理。基于光束传播法,分析平面光波导与阵列光纤对准耦合过程中对准偏差(横向位错、纵向间距和轴向角度)与耦合损耗之间的关系,对对准偏差的光学容差也进行分析。研究结果表明:平面光波导与阵列光纤耦合损耗对横向位错相当敏感,轴向角度偏差对耦合损耗的影响也较大,轴向间距的影响则要小得多;若以0.15 dB的附加损耗考察,平面光波导与阵列光纤横向位错、纵向间距、轴向角度的光学容差分别为1 μm,16 μm和0.65°;所得仿真结果与理论计算结果基本吻合,说明应用光束传播法分析平面光波导与阵列光纤对准耦合是有效的。
关键词:
中图分类号:TN253 文献标识码:A 文章编号:1672-7207(2009)03-0681-06
Coupling analysis between planar optical waveguide and fiber array
ZHENG Yu, DUAN Ji-an
(Key Laboratory of Design for Modern Complex Equipment and Extreme Manufacturing,
Ministry of Education, Central South University, Changsha 410083, China)
Abstract: The theory of aligning and coupling of planar optical waveguide and array fibers was discussed based on optical waveguide principles. The relations between alignment deviation and coupling loss were analyzed based on beam propagation method. The optical tolerance of alignment deviation was studied based on the simulation results. It is found that the coupling loss is sensitive to the transverse dislocation, the second is the angle deviation, and the third is the axial gap. Moreover, when the coupling loss is 0.15 dB, the optical tolerance of the transverse dislocation is 1 μm, the optical tolerance of the angle deviation is 0.65°, and the optical tolerance of the axial gap is 16 μm. The simulation results are in good agreement with the theory results, the analysis for aligning and coupling of planar optical waveguide and array fibers is effective by beam propagation method.
Key words: planar optical lightwave; fiber array; coupling; beam propagation method
平面光波导器件集成了固体物理、材料学、波导光学和微细加工等学科的前沿成果,采用半导体工艺制作平面光波导芯片,将传统分立光学元件的功能集成到同一光学衬底,实现光信号的分束/合束、转换、光滤波等功能[1-4],具有结构紧凑、体积小、抗干扰能力强、性能一致性好、稳定可靠,便于自动化批量生产等突出优势,是目前光电子器件发展的前沿研究课题。波导芯片与器件封装是平面光波导器件制造的2个关键技术[5]。目前,波导芯片的制造技术已日趋成熟。平面光波导器件的封装是利用亚微米精度的运动平台,将波导芯片与阵列光纤进行对准耦合并固 定,是目前光电子器件封装研究的热点问题之一[6-7]。
平面光波导器件的封装需要将数十甚至数百个截面 长×宽为4 μm×4 μm~8 μm×8 μm的波导光通道和芯径为8~9 μm的单模阵列光纤同时进行模场匹配的光学精确对准与耦合[8],任一通道的耦合对准精度不足都将导致器件光信号传输与转换功能丧失。波导芯片与阵列光纤对准耦合理论比较成熟,Saruwateri等[9]分析了半导体激光器与单模光纤的对准耦合,并导出了理论计算公式。该理论公式的前提是假设光场为高斯型分布,实际上,对于波导芯片以及光纤,光场是近似呈高斯型分布,而且该理论公式没有考虑界面反射以及材料吸收等损耗。Murphy等[10]采用硅(单晶硅)基“V”型槽实现平面光波导与阵列光纤的对准与耦合, 但由于硅基为非透明材料,只能通过边缘特征实现初始定位,费时费力。目前,多采用玻璃“V”型槽,该槽透明,可通过视觉的方式观测光纤的特征以实现快速对准,实现平面光波导与阵列光纤的高精度定位与对准耦合[3, 5]。目前,大多数研究基于理论计算公式分析平面光波导与阵列光纤对准耦合,假设的条件过多,例如界面无反射、材料无吸收等[11],因而,分析得出的结论不能全面指导实验。本文作者采用光束传播法(BPM),通过平面光波导与单模阵列光纤耦合仿真,探讨其中的影响机制,以指导平面光波导器件的封装研究。
1 对准耦合模型与理论
关于波导与光纤耦合的理论有很多报道,两者的耦合效率由波导模场与光纤模场之间的重叠积分确 定[12]。波导与光纤之间的连接损耗主要有对准偏差损耗(横向位错损耗、纵向间距损耗、轴向角度损耗)、模场匹配损耗和传输损耗等。前一项损耗取决于波导与光纤对准是否精确,后两项损耗取决于波导与光纤自身的结构,与对准无关。本文作者主要通过光束传播法分析对准偏差对平面光波导器件的影响机理及其规律,以指导其对准封装工艺实验。
1.1 耦合模型
当平面光波导与1根光纤对接时,一共有5个自由度,分别是横向位错x和y,纵向间距z,轴向角度α和β,如图1所示。若是平面光波导与阵列光纤对接时,则有6个自由度,轴向角度多了沿Z轴的θ。任一方向发生改变,都会影响到最终的耦合效率。
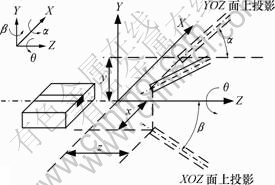
图1 平面光波导与单根光纤对准示意图
Fig.1 Scheme of alignment between planar optical waveguide and single fiber
一般而言,平面光波导的输出通道数不少于4个,各通道的耦合方式以及传输特性相当,故可选取1个通道来进行分析。
1.2 耦合理论
光波导与单模光纤的耦合可用波动理论来计算分析,设光波导中传输的光场为![]() ,光纤中传输的光场为
,光纤中传输的光场为![]() ,则光波导与光纤之间的耦合效率为[12]:
,则光波导与光纤之间的耦合效率为[12]:

如图2所示。

图2 光波导模场与光纤模场间重叠示意图
Fig.2 Scheme of overlap of mode distribution between waveguide and fiber
平面光波导光通道截面有多种形状,如矩形、脊型、扩散型等[12],本文以矩形波导为分析对象。单模矩形波导光通道截面长×宽从3 μm×3 μm~8 μm×8 μm不等,而且由于受制造工艺的制约,波导光通道截面尺寸有一些差异。如若不考虑这些差异,矩形波导的光场分布与光纤的光场分布近似,如图3所示。
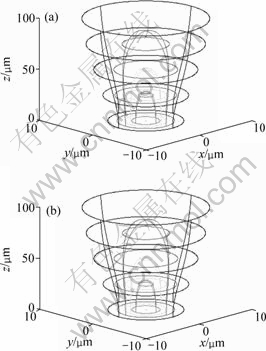
(a) 光纤光场分布(纤芯半径r=4.01 μm); (b) 光波导光场分布(光通道截面长×宽为8 μm×8 μm)
图3 矩形波导与单模光纤的光场分布
Fig.3 Optical field distribution of planar optical waveguide and fiber
2 光束传播法(BPM)原理
光束传播法(BPM)是把波导沿着传播方向划分成若干截面,根据前1个或几个截面上的已知场得到 下1个截面的场分布[13]。它的基础是Helmholtz方程,Helmholtz方程是波动方程在某一频率下的特定方程,使Maxwell方程在特定条件下的特殊形式,是1个二阶的非线性偏微分方程。由于Helmholtz方程是频域方程,解此方程可以得出在某一频率下的稳态解。这一求解过程形象地反映场在波导中的传播与变化 情况。
对于三维波导中![]() 形式的单色波,满足标量方程[14-15]:
形式的单色波,满足标量方程[14-15]:

令![]() ,kn为任意常数,要求它
,kn为任意常数,要求它
的选择应使u(x, y, z)为z的慢变函数![]() ≤
≤![]() 。忽略u关于z的二阶偏导
。忽略u关于z的二阶偏导![]() ,得到傍轴
,得到傍轴
近似的Helmholtz方程:

对于各向同性的矩形波导,在有限差分方法中,沿Z向的XY截面都是由一些离散的点组成,下1个截面的场分布是由已知场分布导出的,因此,可采用2D形式来代替3D形式,从而简化计算。据此可导出式(3)的Crank-Nicholson格式的2D FD-BPM方程。

方程(4)只适用于场矢量的各个分量处处可微的区域。对于光波导与单模光纤耦合模型,由于存在波导与空气2种不同介质,因此,在界面处的场矢量可能不连续,必须加上合理的边界条件。

在二维波导中,Ex,Ez,Hx和Hz中只有分量Ez和Hz是连续的,其余2个分量因为光波在界面入射的角度不同而有突变。为了计算简便,只考虑Ez分量,使得Ez分量在边界保持连续性,这样偏微分方程(1)就在波导内外部和界面统一成立。
以图1建立平面光波导与阵列光纤对准耦合的BPM模型,如图4所示(局部放大)。
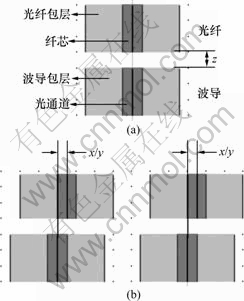
(a) 纵向间距z;(b) 横向位错x/y
图4 平面光波导与单模光纤仿真模型
Fig.4 Simulation model of planar optical waveguide and single fiber
仿真计算参数如下:波长λ=1.55 nm,单模光纤芯径D=8.02 μm,波导光通导截面长×宽为8 μm×8 μm,波导与光纤包层的折射率设定为一致(nCladding=1.445),光通道与包层的折射率差Δn=0.3%。
3 计算结果分析与讨论
光束传播法的原理就是波导沿着传播方向划分成若干截面,根据前1个或几个截面上的已知场得到下1个截面的场分布。在此,为了计算方便,只考虑Ez分量,如图5所示。图5(a)所示为光在波导中的传播过程,图5(b)所示为沿着传播方向功率的变化曲线,由此可计算出功率的损耗。
由平面光波导与光纤结构的对称性可知,偏差x和y所引起的光功率损耗是相等的;轴向角α和β引起的光功率损耗也是相等的。
根据式(1)计算可知,在没有对准误差时,也存在光功率损耗,约为0.002 1 dB,也就是说,平面光波导与光纤的耦合效率不可能达到100%,因为矩形波导的模场与光纤的模场不可能完全匹配,总是存在一定的偏差。仿真结果也是如此,光功率损耗为0.003 dB,比理论结果略大。平面光波导与光纤的理论耦合效率取决于两者模场的重叠积分,没有考虑传输介质对光功率的影响。而光束传播法考虑了这些因素,所以,计算结果较理论结果精确。
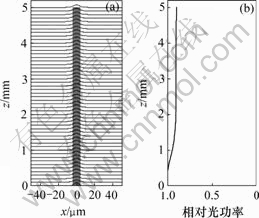
(a) 光在波导中的传播过程;(b) 光沿传播方向功率的变化
图5 纵向间隙z=35 μm时的仿真结果
Fig.5 Simulation results when axial gap is 35 μm
3.1 横向位错
横向位错主要是沿着X与Y方向的对准偏差x和y。根据图6可知,两者之间的耦合效率随着横向位错的增加而呈指数规律急剧增加。光功率损耗仿真曲线与理论曲线在横向位错小于1 μm时,两者相差较小;当横向位错大于1 μm时,仿真结果与理论计算结果相差较大。
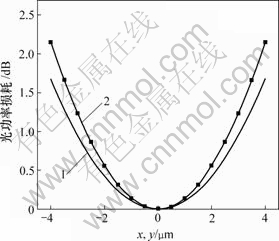
1—理论曲线;2—仿真曲线
图6 平面光波导横向位错与光功率损耗的关系
Fig.6 Relations between transverse dislocation and optical power loss for planar optical lightwave
以0.15 dB的附加损耗考察,对应的耦合效率为96.5%,此时,理论横向位错x或y为1.1721 μm,而仿真结果为1.029 5 μm。据此可知:如果使横向位错附加损耗低于0.15 dB,那么横向位错光学容差为 1 μm。
3.2 纵向间距
纵向间距与光功率损耗的关系见图7。由图7可知,纵向间距引起的附加损耗变化较慢,仿真结果与理论上的规律基本一致,在z=50 μm时,附加损耗约为1 dB。
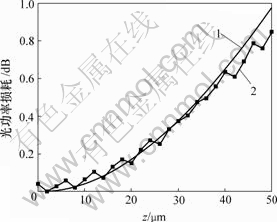
1—理论曲线;2—仿真曲线
图7 平面光波导纵向间距与光功率损耗关系
Fig.7 Relations between axial gap and optical power loss for planar optical lightwave
值得注意的是,在z=0 μm时,光功率损耗仿真结果为0.043 dB,比理论结果大很多;而当存在一定的间距时,损耗相对较小。当间距较小时,平面光波导与光纤模场的不匹配对附加损耗影响较大;适当存在一定的间距,则可使平面光波导的发散场处于光纤的接收角之内,从而可减小附加损耗。事实上,平面光波导与光纤纵向间距不可能为零,因为两者之间还要填充一层折射率匹配的胶液,使两者牢固地粘接在一起。纵向间距过大,光场发散角大于接收波导的接收角,致使光信号进入包层,从而引起较大的光功率损耗。此处,理论计算结果与仿真结果均为考虑了界面的反射光功率损耗,也称菲涅尔损耗。
同样,以0.15 dB的附加损耗考察,此时,理论纵向间距为18.595 4 μm,而仿真结果为16.917 6 μm。据此可知:如果使纵向间距附加损耗低于0.15 dB,那么,纵向间距光学容差小于16 μm。
3.3 轴向角度
轴向角度主要是沿着绕X轴与Y轴的角度偏差α和β。由图8可知,光功率损耗理论结果比仿真结果要小,特别是角度偏差较大时更是如此。理论附加损耗随着角度偏差的增加而缓慢增加,仿真结果则呈指数规律急剧增大。光功率损耗理论结果是根据平面光波导与光纤模场重叠面积计算而来的,而这一部分的光信号有一部分耦合进了包层,在包层中传输的光信号几乎全部损耗,所以,角度偏差越大,进入到包层的光信号越多,损耗也就越大。
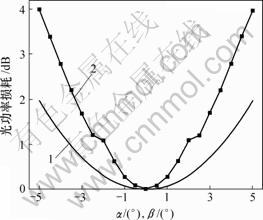
1—理论曲线;2—仿真曲线
图8 平面波导轴向角度与光功率损耗关系
Fig.8 Relation between angle deviation and optical power loss for planar optical lightwave
同样,以0.15 dB的附加光功率损耗考察,此时,理论轴向角度偏差为1.362 1?,而仿真结果为0.650 1?。据此可知:如果使轴向角度偏差损耗低于0.15 dB,那么,轴向角度光学容差为0.65?。
4 结 论
a. 光功率损耗仿真结果与理论结果变化趋势一致,表明仿真计算结果是有效的,并且仿真结果较理论结果精确。
b. 平面光波导与光纤的耦合效率随着横向位错的增加而呈指数规律急剧增加。
c. 平面光波导与光纤耦合效率对横向位错相当敏感,而轴向间距的影响则要小得多,轴向角度偏差对耦合效率的影响也较大。
d. 当附加光功率损耗为0.15 dB时,平面光波导与光纤横向位错、纵向间距、轴向角度容差分别为 1 μm,16 μm和0.65?。
参考文献:
[1] Doerr C R, Okamoto. Advances in silica planar lightwave circuit[J]. Journal of Lightwave Technology, 2006, 24(12): 4763-4789.
[2] Poulsen M R, Borel P I, Fage-Pedersen J, et al. Advances in silica-based integrated optics[J]. Optical Engineering, 2003, 42(10): 2821-2834.
[3] Bogaerts W, Baets R, Dumon P, et al. Nanophotonic waveguides in silicon-on-insulator fabricated with CMOS technology[J]. Journal of Lightwave Technology, 2005, 23(1): 401-412.
[4] Eldada L, Shacklette L W. Advances in polymer integrated optics[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2000, 6(1): 54-68.
[5] Ray C. Packaging and integration of high-speed optical components[J]. IEEE Instrumentation & Measurement Magazine, 2004, 7(2): 60-62.
[6] ZHANF Rong. Study of novel algorithms for fiber-optic alignment and packaging automation[D]. Irvine: Beckman Laser Institute, University of California, 2003.
[7] Murakawa M, Nosato H, Higuchi T. Automatic optical fiber alignment system using genetic algorithms[C]//The 6th International Conference on Artificial Evolution. Marseilles: Springer, Berlin, 2003: 129-140.
[8] Kawachi M. Silica waveguides on silicon and their application to integrated-optic components[J]. Optical and Quantum Electronics, 1990,22(5): 391-416.
[9] Saruwateri M, Nawata K. Semiconductor laser to single-mode fiber coupler[J]. Applied Optics, 1979, 18(11): 1847-1856.
[10] Murphy E J, Rice T C. Permanent attachment of single mode fiber arrays to wave-guide[J]. Journal of Lightwave Techmology, 1985, 3(1): 795-799.
[11] 孙蓉霞, 陈抱雪, 隋国荣, 等. 波导阵列与光纤阵列的遗传算法自动对接[J]. 光学技术, 2006, 32(4): 533-536.
SUN Rong-xia, CHEN Bao-xue, SUI Guo-rong, et al. Automation alignment between waveguide array and fiber array based on genetic algorithm[J]. Optical Technique, 2006, 32(4): 533-536.
[12] Okamoto. Fundamentals of optical waveguide[M]. New York: Academic Press, 2001: 51-70.
[13] Doerr C R. Beam propagation method tailored for step-index waveguides[J]. IEEE Photonics Technology Letter, 2001, 13(2): 130-132.
[14] Scarmozzino R, Osgood R M. Comparison of finite-difference and fourier-transform solutions of the parabolic wave equation with emphasis on integrated optics applications[J]. Journal of the Optical Society of America A, 1991, 8(5): 724-731.
[15] 吴宇列, 郑 煜, 王金娥, 等. 熊猫型保偏光纤定轴仿真研究[J]. 光子学报, 2007, 36(7): 1224-1229.
WU Yu-lie, ZHENG Yu, WANF Jin-e, et al. Research of azimuthal alignment for PANDA fiber[J]. Acta Photonica Silica, 2007, 36(7): 1224-1229.
收稿日期:2008-06-19;修回日期:2008-09-18
基金项目:国家自然科学基金重点资助项目(50735007);国家“863”高技术研究发展计划项目(2007AA04Z344)
通信作者:段吉安(1969-),男,湖南冷水江人,教授,从事集成光子器件封装技术研究;电话:0731-8836858;E-mail: duanjian@mail.csu.edu.cn
[12] Okamoto. Fundamentals of optical waveguide[M]. New York: Academic Press, 2001: 51-70.
" target="blank">[15] 吴宇列, 郑 煜, 王金娥, 等. 熊猫型保偏光纤定轴仿真研究[J]. 光子学报, 2007, 36(7): 1224-1229.WU Yu-lie, ZHENG Yu, WANF Jin-e, et al. Research of azimuthal alignment for PANDA fiber[J]. Acta Photonica Silica, 2007, 36(7): 1224-1229.


