DOI: 10.11817/j.issn.1672-7207.2015.10.031
复杂边界条件下崩落矿岩流动特性
孙浩,金爱兵,高永涛,周喻,杨振伟
(北京科技大学 金属矿山高效开采与安全教育部重点实验室,北京,100083)
摘 要:
和PFC3D程序,构建放矿模型,开展对倾斜矿体复杂边界条件下崩落矿岩流动特性的研究,实现放出体(IEZ)形态的可视化。同时,将模拟结果与已有研究结论进行对比,验证基于PFC程序的放矿模型在崩落矿岩流动特性研究中的适用性与可靠性。研究结果表明:因受到倾斜边壁的限制,在复杂边界条件下放出体形态产生不同程度的变异,并不是一个规则的椭球体;在3类边界条件下,在放矿初始阶段,放出体高度呈指数形式快速增加,随着放矿量的增加,其增长率逐渐减小,随后,放出体高度将随放矿量的增加呈线性增长;下盘残留量随矿石层初始高度与矿石水平厚度之比(H/T)的增加而增加,其增长率逐渐降低,而随矿体倾角的增加而明显降低。
关键词:
中图分类号:TD85 文献标志码:A 文章编号:1672-7207(2015)10-3782-07
Flow characteristics of caved ore and rock under complex boundary conditions
SUN Hao, JIN Aibing, GAO Yongtao, ZHOU Yu, YANG Zhenwei
(Key Laboratory of Ministry of Education for Efficient Mining and Safety of Metal Mine,
University of Science and Technology Beijing, Beijing 100083, China)
Abstract: Based on particle flow theory and PFC3D code, draw model was constructed to study the flow characteristics of caved ore and rock at the complex boundary conditions in order to realize the visualization of the isolated extraction zone (IEZ) form. Simultaneously, the suitability and reliability of draw model based on PFC code and used in flow characteristics research of caved ore and rock were validated by comparative analysis between simulated results and existing research conclusions. The results show that the IEZ form produces different degrees of variation under complex boundary conditions due to the limit of tilting side walls, and thus the IEZ form is not a regular ellipsoid. The height of the IEZ increases rapidly in the form of index at the initiation of draw and its growth rate decreases with the increase of mass drawn, while the height of the IEZ increases linearly with the increase of mass drawn when mass drawn reaches a constant value. The footwall residual amounts increase as the ratio of initial ore layer height and ore level thickness (H/T) increases, and the increase rate decreases gradually but it reduces obviously as the increase of the orebody dips.
Key words:PFC3D code; complex boundary condition; caved ore and rock; flow characteristics
采矿边界条件与崩落矿岩流动特性关系密切,直接影响到矿岩界面的移动过程、矿石残留体的空间位置、形态和数量以及放出体的形态和空间位置等,从而影响矿石回收指标:因此,采场边界条件对崩落矿岩流动特性的影响一直是放矿领域研究的重点之一[1]。根据放矿边界条件的特点,边界条件分为3类:第一类为无限边界条件,第二类为半无限边界条件,第三类为复杂(倾斜壁)边界条件。其中,复杂边界条件是指在崩落法采矿中,当矿体倾角大于崩落矿岩自然安息角而小于90°时,影响崩落矿岩移动的采场边界条件[2]。在复杂边界条件下,放出体的形态发生变异,因此,包括椭球体放矿理论[3]在内的以放出体为基础的传统研究方法不太适用。除此之外,随机介质放矿理论[2,4]在复杂边界条件下基于散体移动概率密度方程推导的散体移动速度、颗粒移动迹线、放出体形态等与许多研究者所进行的室内物理模拟试验结果相符,且仿真度较高,解决问题有效性强,因而在实际中有着广泛的应用。但这种研究思路基于宏观统计学思想,并未依据力学机理这一放矿过程的本质去研究其演化规律[5]。计算机仿真技术在放矿研究中的应用[6-8]较广泛,同时也很便捷,如可随机模拟采场结构参数及矿体条件对矿石回收指标的影响。现有放矿仿真模拟技术[9-11]无论是基于有限单元法(FEM)的放矿模型还是基于元胞自动机理论(CA)的放矿模型或软件,大多仅限于第一和二类边界条件,对第三类边界条件下的放矿问题并未很好地解决。而在实际生产中,多数采场的放矿受到边界条件的影响,复杂边界条件更为常见。因此,须使用更合适的理论指导复杂边界条件下的放矿仿真模拟。PFC是基于细观离散元理论(又称为颗粒元理论)开发的一种商业数值软件,主要应用于岩石类材料基本特性、岩石类介质破裂机理与演化规律、颗粒物质动力响应等基础性问题的研究,其思想是借助作为介质中最基本单元的粒子和作为最基本力学关系的粒子间的牛顿第二定律来描述介质的复杂力学行为[12]。PFC软件能够从细观角度对复杂边界条件下崩落矿岩流动特性进行本质性分析和描述[13-14],为此,本文借助基于细观离散元法的PFC3D程序,构建模型对复杂边界条件下崩落矿岩流动特性进行研究。
1 数值模拟实现过程
1.1 模型构建与设置
综合考虑矿山放矿现状及计算机处理能力,本数值试验放矿模型长×宽×高为12 m×12 m×30 m,孔隙率为0.50,放矿口长×宽为3.0 m×3.0 m,颗粒半径为0.3 m,颗粒黏结采用无黏结模型,颗粒生成采用半径扩大法。图1所示为模型墙体结构,其中,图1(a)中若删除垂直于y轴的8号侧墙,则为第一类边界条件下的试验模型,若设置8号侧墙,则为第二类边界条件下的试验模型;而图1(b)为复杂边界条件下的倾斜角度为65°的试验模型。图中第1,2和3号底墙分别代表不同试验中试验的放矿口。整个放矿过程可分为以下3个阶段。
1) 在模型内指定区域随机生成一定数量颗粒使模型初始孔隙率达0.50。
2) 赋予颗粒重力加速度g=-9.81 m/s2,并赋予墙体及颗粒指定的细观力学参数,使整个模型达初始平衡状态。采用的相应墙体及颗粒细观力学参数如下:墙体法向刚度为1×109 N/m,切向刚度为1×109 N/m,摩擦因数为0.50;颗粒的法向刚度为1×108 N/m,切向刚度为1×108 N/m,颗粒密度为2 880 kg/m3,摩擦因数为0.50。
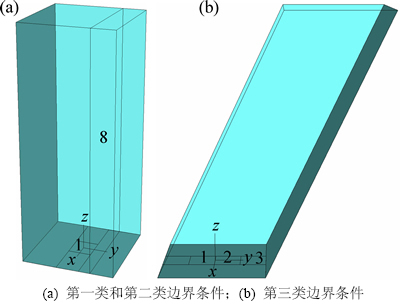
图1 模型墙体结构示意图
Fig. 1 Schematic diagrams of wall structures of models
3) 在删除图2中代表放矿口的正方形底墙后,散体颗粒将从放矿口不断向下排出,放矿过程随之开始;当放出量达设定值时,关闭代表放矿口的相应底墙,放矿过程随之结束。
放矿过程中借助PFC3D程序中自带的FISH[15]语言,通过编译程序记录模型达到初始平衡状态时,每个颗粒坐标及达到不同放矿量时放出颗粒ID号,即可得每个放出颗粒在初始平衡时的位置,这部分颗粒所形成的区域即为放出体。通过上述程序可以实现放出体形态的可视化,真实直观地描述放出体的位置并计算放出体高度等信息。
1.2 试验设计
在模型整体面积及散体颗粒性质相同的情况下,通过比较3类边界条件下放出体形态、放出体高度与放矿量的关系等方面的异同,以及分析颗粒速度与接触力的分布特征,研究复杂边界条件对崩落矿岩流动特性的影响。分别在无限和半无限边界条件下各进行1次试验,在复杂边界条件下设置不同的放矿口位置进行3次试验,因此,共进行5次数值试验。每次试验依次记录20,50,80,140,200,300,400,500,600,800,1 000和1 400 t共12个不同放矿量时放出体的高度。图2所示为放出体IEZ(isolated extraction zone)及松动体IMZ(isolated movement zone)的主要参数,图2中:hIEZ和hIMZ分别为放出体及松动体的高度;wIEZ和wIMZ分别为放出体及松动体的宽度。
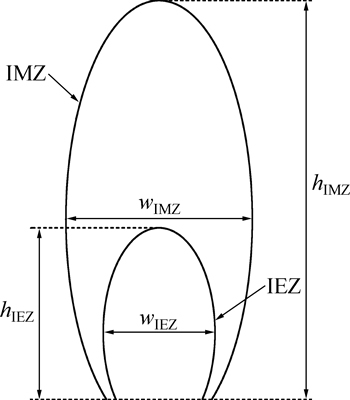
图2 放出体及松动体的主要参数示意图
Fig. 2 Schematic diagram of major parameters of IEZ and IMZ
2 计算结果分析
为探究复杂边界条件下崩落矿岩的流动特性,验证基于PFC3D程序的放矿模型在崩落矿岩流动特性研究中的适用性与可靠性,对放出体拟合形态、放出体高度与放矿量的关系等进行分析。
2.1 放出体拟合形态
对3类边界条件下放出体形态进行拟合,图3所示为5组试验中放矿量达1 400 t时的放出体形态,其中,第1行为沿x轴方向的放出体形态,第2行为沿y轴方向的放出体形态。由图3可见:沿x轴方向即显示放出体不受边界条件影响的一侧,放出体形态均近似截头椭球体,但沿y轴方向即显示放出体受边界条件影响的一侧,放出体形态各异。具体而言,第一类边界条件下放出体形态完整,近似椭球体;第二类边界条件下因受垂直边壁的限制,放出体形态不完整,但仍可将其形态近似视为椭球体的一部分;第三类边界条件下因受到倾斜边壁的限制,放出体形态产生不同程度的变异,并不是1个规则的椭球体。此外,记录放出体颗粒在初始平衡时的坐标,通过反演分析即可实现放出体在模型中具体位置的可视化,并能在整个放矿过程中监测放出体演化过程。以试验5为例,图4所示为该试验中放出体在模型中的位置剖面图,其中颗粒所围成区域即为放出体。

图3 5组试验放出体形态示意图
Fig. 3 Schematic diagrams of IEZ forms of 5 groups of experiments
2.2 PFC模拟可靠性检验
Castro等[16]以砾石为介质开展迄今为止规模最大的崩落法采矿中矿岩流动特性的三维物理放矿试验研究,其模型主体结构长×宽×高为2.5m×3.5 m×3.3 m。该物理试验为第一类边界条件下放矿试验,通过放出标志颗粒在初始平衡时的不同位置,确定放出体的高度和最大宽度等信息。其试验研究得放出体高度hIEZ与累计放矿量m之间满足
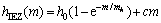 (1)
(1)
式中:方程系数h0和mh分别为随着放矿量的增加,放出体的高度呈指数形式增加时的高度和质量;c为最终放出体高度随放矿量线性增加时的增长率。
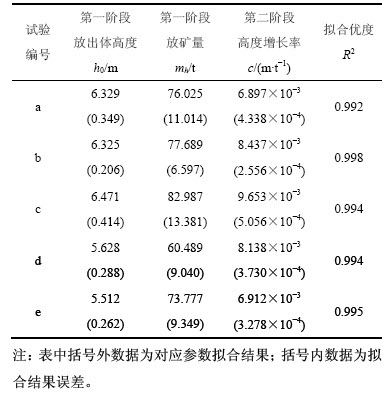
为进行模型适用性及可靠性分析,在本次模拟试验中,分别统计5次试验中达到所设置的12个放矿量时的放出体高度,基于Levenberg-Marquardt算法用式(1)对模拟试验数据进行检验,其系数拟合结果见表1(表中各拟合系数括号内的数据为相应拟合系数的误差)。
由表1可知:各试验的拟合优度R2均接近1,表明由式(1)所得结果与模拟试验结果高度拟合。其中,式(1)为在第一类边界条件下物理实验所得结论,因此,试验a所得结果的高度拟合说明本次试验构建的模型能够反映放矿实际情况,即验证了基于PFC3D程序的放矿模型在崩落矿岩流动特性研究中的适用性与可靠性;而第二类和第三类边界条件下的试验b~e所得结果的高度拟合则拓宽了式(1)的适用范围,即得出结论:这3类边界条件下放出体高度与放矿量均满足式(1)所示的关系。
2.3 放出体高度与放矿量关系
以试验b为例,图5所示为放出体高度理论曲线与试验b所得结果的对比。由图5可见:放出体高度的变化趋势可分为2个阶段:第一阶段是在放矿初始阶段,放出体高度呈指数形式快速增加,随着放矿量的增加,其增长率逐渐减小;第二阶段,放出体高度将随放矿量的增加而线性增长。

图4 放出体在模型中位置剖面图
Fig. 4 Profile of position of IEZ in model
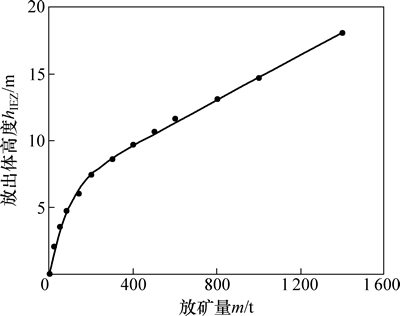
图5 放出体高度理论曲线与试验数据对比
Fig. 5 Comparison of theory curve and experimental data of height of IEZ
表1 式(1)中相关参数拟合结果
Table 1 Fitting results of relevant parameters in Eq. (1)
通过调整墙体、颗粒直径及细观力学参数重复上述试验过程,发现式(1)对各模拟试验数据依然高度拟合。该结论可有效分析并判断不同边界条件,尤其是在复杂边界条件下,不同放矿阶段时的放出体结构及其生成与演化规律。
3 下盘残留量模拟
崩落法放矿后的矿石损失形式主要包括脊部残留与下盘残留[1]。残留在放矿口之间的矿石为脊部残留,残留在下盘面上的矿石为下盘残留,如图6所示。根据不同矿体水平厚度T、矿石层初始高度H及矿体倾角α等参数,脊部残留的大部分矿石能够在下分段或阶段被再次回收,下盘残留若不采取一定措施,则将无法再次回收而永久损失,因此,有必要借助PFC3D程序构建模型分析下盘残留矿石损失的主要形式。
一般而言,下盘残留的空间位置、形态及数量主要受崩落矿岩的放出空间条件的影响,因此,本次试验通过构建若干复杂边界条件下放矿模型分析下盘残留与矿体水平厚度T、矿石层初始高度H及矿体倾角α这3个放出空间条件的关系,H/T取值分别为0.5,1.0,1.5,2.0及2.5,α取值分别为50°,60°,70°及80°。采用低贫化放矿方式[17-20],放出的颗粒中出现废石颗粒就停止放矿,以降低矿石贫化率。由于不考虑脊部残留,故该试验只在如图1(b)中所示第3号底墙的位置即紧邻矿体下盘边壁左侧设置1个放矿口。模型内除矿石颗粒密度为4.0 t/m3、废石颗粒密度为 2.7 t/m3之外,其余整体结构及颗粒物理力学性质均不变,矿石层及废石层初始高度均为H。
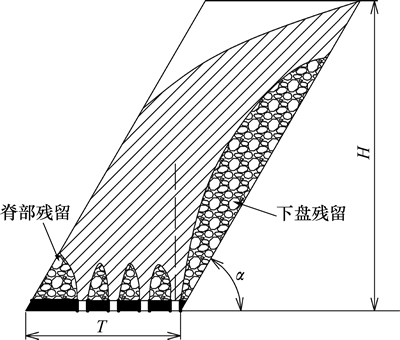
图6 复杂边界条件放矿时的矿石损失形式
Fig. 6 Ore loss form when drawing at complex boundary condition
以参数H/T=1.5,α=60°的试验为例,图7所示为其停止放矿时不同颗粒位置分布,其中,区域A表示脊部残留且已放出矿石,区域B为岩石,而区域C为下盘残留。由图7可见:下盘残留的空间位置及形态与大多数物理试验及矿山放矿实际结果一致,而下盘残留量占总矿石量的比β达25.678%。图8所示为本次试验下盘残留量与矿体相关参数的关系。由图8可见:下盘残留量随H/T的增加而增加,其增长率逐渐降低;而下盘残留量随矿体倾角的增加而明显降低。依据上述分析结果并结合放矿实际,若要减少下盘损失,则除采取开掘下盘岩石及在下盘岩石中布置放矿口等措施外,一般而言,可适当降低矿石层高度;而当矿体下盘倾角很大(如80°)时,在放矿允许的条件下,应尽量增大矿石层高度。在此基础上,应综合考虑开掘工程量及贫化率等指标,根据利润最大原则确定合理的放矿结构参数。
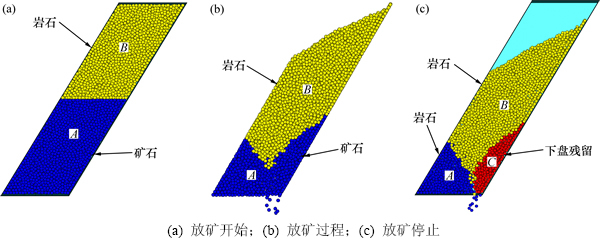
图7 停止放矿时不同颗粒位置分布
Fig. 7 Distributions of different particle positions when stopping drawing
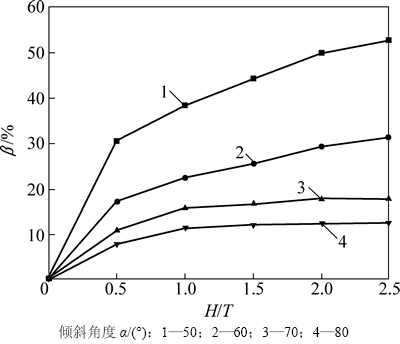
图8 下盘残留量与矿体相关参数的关系
Fig. 8 Relationship between footwall residual amounts and related orebody parameters
4 结论
1) 在倾斜边壁的影响下,复杂边界条件下放出体形态产生不同程度的变异,并不是一个规则的椭球体。
2) 在3类边界条件下放出体高度的变化趋势均可分为以下2个阶段:在放矿初始阶段,放出体高度呈指数形式快速增长,随着放矿量的增加,其增长率在逐渐减小;随后,放出体高度将随放矿量的增加呈线性增长。
3) 下盘残留量随H/T的增加而增加随矿体倾角的增加明显降低。
4) 一般而言,适当降低矿石层高度可减小下盘损失;而对于下盘倾角较大的矿体而言,在放矿允许的条件下,应尽量增大矿石层高度。在此基础上,应综合考虑开掘工程量及贫化率等技术经济指标,并根据利润最大化原则确定合理的放矿结构参数。
5) 基于PFC的崩落矿岩流动特性研究可弥补现有室内试验研究及数值计算的不足,可以作为一种有效手段对复杂边界条件下散体矿岩放矿运移机理进行研究。
参考文献:
[1] 张志贵, 刘兴国, 于国立. 无底柱分段崩落法无贫化放矿: 无贫化放矿理论及其在矿山的实践[M]. 沈阳: 东北大学出版社, 2007: 6-58.
ZHANG Zhigui, LIU Xingguo, YU Guoli. Sublevel caving method without sill pillars in the base of undiluted ore drawing: Undiluted ore drawing theory and its practice in mine[M]. Shenyang: Northeastern University Press, 2007: 6-58.
[2] 周宗红. 倾斜中厚矿体损失贫化控制理论与实践[M]. 北京: 冶金工业出版社, 2011: 1-35.
ZHOU Zonghong. Loss and dilution control theory and practice of dipping medium thick orebody[M]. Beijing: Metallurgical Industry Press, 2011: 1-35.
[3] 王汉昌. 放矿学[M]. 北京: 冶金工业出版社, 1982: 39-87.
WANG Hanchang. Ore drawing[M]. Beijing: Metallurgical Industry Press, 1982: 39-87.
[4] 李彬. 武钢程潮铁矿采场放矿规律及放矿步距优化研究[D]. 武汉: 武汉科技大学资源与环境工程学院, 2012: 7-13.
LI Bin. Investigation of law ore drawing and step optimize in Chengchao Iron Mine of Wugang[D]. Wuhan: Wuhan University of Science and Technology. School of Resource and Environmental Engineering, 2012: 7-13.
[5] 王培涛, 杨天鸿, 柳小波. 无底柱分段崩落法放矿规律的PFC2D模拟仿真[J]. 金属矿山, 2010(8): 123-127.
WANG Peitao, YANG Tianhong, LIU Xiaobo. PFC2D numerical simulation of ore drawing rule with pillarless sublevel caving[J]. Metal Mine, 2010(8): 123-127.
[6] 柳小波, 李启轩, 孙豁然, 等. 计算机仿真放矿移动概率赋值问题的商榷[J]. 东北大学学报(自然科学版), 2007, 28(1): 115-117.
LIU Xiaobo, LI Qixuan, SUN Huoran, et al. Discussion on valuation of movement probability during ore-drawing computer-simulated[J]. Journal of Northeastern University (Natural Science), 2007, 28(1): 115-117.
[7] 焦健, 乔春生, 徐干成. 开挖模拟在数值流形方法中的实现[J]. 岩土力学, 2010, 31(9): 2951-2957.
JIAO Jian, QIAO Chunsheng, XU Gancheng. Simulation of excavation in numerical manifold method[J]. Rock and Soil Mechanics, 2010, 31(9): 2951-2957.
[8] 徐帅, 安龙, 冯夏庭, 等. 急斜薄矿脉崩落矿岩散体流动规律研究[J]. 东采矿与安全工程学报, 2013, 30(4): 512-517.
XU Shuai, AN Long, FENG Xiating, et al. Research on granular flow laws of caved ore and rock for steeply dipping thin vein[J]. Journal of Mining and Safety Engineering, 2013, 30(4): 512-517.
[9] Castro R. Study of the mechanisms of gravity flow for block caving[D]. Queensland: University of Queensland. Sustainable Minerals Institute, 2006: 7-34 .
[10] Chitombo G P. Caving mining—16 years after Laubscher’s 1994 paper ‘Cave mining-state of the art’[C]//Proceedings of the 2nd International Symposium on Block and Sublevel Caving. Perth, Australia, 2010: 45-61.
[11] Castro R, Gonzales F, Arancibia E. Development of a gravity flow numerical model for the evaluation of drawpoint spacing for block/panel caving[J]. Journal of the Southern African Institution of Mining and Metallurgy, 2009, 109(7): 393-400.
[12] Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47-65.
[13] 朱焕春. PFC及其在矿山崩落开采研究中的应用[J]. 岩石力学与工程学报, 2006, 25(9): 1927-1931.
ZHU Huanchun. PFC and application case of caving study[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(9): 1927-1931.
[14] 王家臣, 魏立科, 张锦旺, 等. 综放开采顶煤放出规律三维数值模拟[J]. 煤炭学报, 2013, 38(11): 1905-1911.
WANG Jiachen, WEI Like, ZHANG Jinwang, et al. 3D numerical simulation on the top-coal movement law under caving mining technique[J]. Journal of China Coal Society, 2013, 38(11): 1905-1911.
[15] Itasca Consulting Group. PFC3D (particle flow code in 3 dimensions) FISH in PFC3D[M]. Minnesota: Itasca Consulting Group Inc, 2008: 13-127.
[16] Castro R, Trueman R, Halim A. A study of isolated draw zones in block caving mines by means of a large 3D physical model[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 860-870.
[17] 程爱平. 金山店铁矿低贫化放矿试验与应用研究[D]. 武汉: 武汉科技大学资源与环境工程学院, 2011: 17-47.
CHENG Aiping. An experimental and application study of low dilution ore drawing in Jinshandian Iron Mine[D]. Wuhan: Wuhan University of Science and Technology. School of Resource and Environmental Engineering, 2011: 17-47.
[18] 仝庆亮, 严荣富. 低贫化放矿的PFC2D数值模拟[J]. 现代矿业. 2014(3): 1-3.
TONG Qingliang, YAN Rongfu. Numerical simulation research on the low dilution drawing based on PFC2D[J]. Modern Mining, 2014(3): 1-3.
[19] 陆玉根, 章林, 孙国权, 等. 高变分段低贫化放矿及其参数优化试验研究[J]. 金属矿山, 2014(4): 12-16.
LU Yugen, ZHANG Lin, SUN Guoquan, et al. Experimental study on low dilution drawing of high and variable sublevel and its parameter optimization[J]. Metal Mine, 2014(4): 12-16.
[20] 张巍元. 低贫化放矿的三维数值模拟研究[D]. 哈尔滨:哈尔滨工业大学土木工程学院, 2013: 2-21.
ZHANG Weiyuan. Research on 3-D modeling low dilution for mine[D]. Harbin: Harbin Institute of Technology. School of Civil Engineering, 2013: 2-21.
(编辑 刘锦伟)
收稿日期:2014-10-11;修回日期:2015-01-08
基金项目(Foundation item):国家自然科学基金资助项目(51374032);科技北京百名领军人才培养工程(Z151100000315014)(Project (51374032) supported by the National Natural Science Foundation of China; Project (Z151100000315014) supported by Beijing Training Project for the Leading Talents in S & T)
通信作者:金爱兵,博士,副教授,从事采矿工程及岩土工程灾害治理研究;E-mail:jinaibing@ustb.edu.cn
摘要:基于颗粒元理论和PFC3D程序,构建放矿模型,开展对倾斜矿体复杂边界条件下崩落矿岩流动特性的研究,实现放出体(IEZ)形态的可视化。同时,将模拟结果与已有研究结论进行对比,验证基于PFC程序的放矿模型在崩落矿岩流动特性研究中的适用性与可靠性。研究结果表明:因受到倾斜边壁的限制,在复杂边界条件下放出体形态产生不同程度的变异,并不是一个规则的椭球体;在3类边界条件下,在放矿初始阶段,放出体高度呈指数形式快速增加,随着放矿量的增加,其增长率逐渐减小,随后,放出体高度将随放矿量的增加呈线性增长;下盘残留量随矿石层初始高度与矿石水平厚度之比(H/T)的增加而增加,其增长率逐渐降低,而随矿体倾角的增加而明显降低。
[1] 张志贵, 刘兴国, 于国立. 无底柱分段崩落法无贫化放矿: 无贫化放矿理论及其在矿山的实践[M]. 沈阳: 东北大学出版社, 2007: 6-58.
[2] 周宗红. 倾斜中厚矿体损失贫化控制理论与实践[M]. 北京: 冶金工业出版社, 2011: 1-35.
[3] 王汉昌. 放矿学[M]. 北京: 冶金工业出版社, 1982: 39-87.
[4] 李彬. 武钢程潮铁矿采场放矿规律及放矿步距优化研究[D]. 武汉: 武汉科技大学资源与环境工程学院, 2012: 7-13.
[5] 王培涛, 杨天鸿, 柳小波. 无底柱分段崩落法放矿规律的PFC2D模拟仿真[J]. 金属矿山, 2010(8): 123-127.
[6] 柳小波, 李启轩, 孙豁然, 等. 计算机仿真放矿移动概率赋值问题的商榷[J]. 东北大学学报(自然科学版), 2007, 28(1): 115-117.
[7] 焦健, 乔春生, 徐干成. 开挖模拟在数值流形方法中的实现[J]. 岩土力学, 2010, 31(9): 2951-2957.
[8] 徐帅, 安龙, 冯夏庭, 等. 急斜薄矿脉崩落矿岩散体流动规律研究[J]. 东采矿与安全工程学报, 2013, 30(4): 512-517.
[13] 朱焕春. PFC及其在矿山崩落开采研究中的应用[J]. 岩石力学与工程学报, 2006, 25(9): 1927-1931.
[14] 王家臣, 魏立科, 张锦旺, 等. 综放开采顶煤放出规律三维数值模拟[J]. 煤炭学报, 2013, 38(11): 1905-1911.
[17] 程爱平. 金山店铁矿低贫化放矿试验与应用研究[D]. 武汉: 武汉科技大学资源与环境工程学院, 2011: 17-47.
[18] 仝庆亮, 严荣富. 低贫化放矿的PFC2D数值模拟[J]. 现代矿业. 2014(3): 1-3.
[19] 陆玉根, 章林, 孙国权, 等. 高变分段低贫化放矿及其参数优化试验研究[J]. 金属矿山, 2014(4): 12-16.


