J. Cent. South Univ. Technol. (2009) 16: 0451-0457

DOI: 10.1007/s11771-009-0076-5

Stability and nonlinear dynamic behavior of drilling shaft system in copper stave deep hole drilling

Kong Ling-fei(孔令飞), Li Yan(李 言), L? Yan-jun(吕延军),

Li De-xin(李德信), Li Shu-juan(李淑娟), TANG Ao-fei(汤奥斐)

(School of Mechanical and Instrumental Engineering, Xi’an University of Technology, Xi’an 710048, China)

Abstract: The stability and nonlinear dynamic behavior of drilling shaft system in copper stave deep hole drilling were analyzed. The effects of the fluctuation of the cutting force, the mass eccentricity and the hydrodynamic forces of cutting fluid could be taken into consideration in the model of drilling shaft system. Based on the isoparametric finite element method, the variational form of Reynolds equation in hydrodynamic fluid was used to calculate nonlinear hydrodynamic forces and their Jacobian matrices simultaneously. In the stability analysis, a new shooting method for rapidly determining the periodic orbit of the nonlinear drilling shaft system and its period was presented by rebuilding the traditional shooting method and changing the time scale. Through the combination of theories with experiment, the correctness and effectiveness of the above methods are verified by using the Floquet theory. The results show that the mass eccentricity can inhibit the whirling motion of drilling shaft to some extent.

Key words: copper stave; deep hole drilling; drilling shaft; nonlinearity; bifurcation

1 Introduction

The copper stave is a new kind of cooling equipment. Compared with the cast iron stave, its cooling efficiency is much higher, which can satisfy the need of thermal load greatly and make the furnace life more than 20 years [1]. However, the slot hole drilling has become a bottleneck problem on the development of copper stave due to the structural particularity and drilling difficulty. The drilling process and cutting mechanism of slot hole have no major difference compared with the traditional round hole drilling, while the stability of drilling shaft and processing quality are worse. Therefore, early researches on deep hole drilling have paid much attention to the stability and effective control of the drilling shaft system.

EMA et al studied chatter vibration [2] and whirl vibration [3-5], explained how whirling vibration in drilling resulted in distorted polygonlike holes with an odd number of sides, and identified whirling as a self-excited vibration. A mathematical model was presented by BATZER et al [6] for a chisel drill to determine the dynamic behaviors of the assumed rigid tool and rigid workpiece, where they only considered the axial vibration and ignored the transverse motion. They used a single degree of freedom model to numerically study the dynamic behaviors of drilling shaft. MATIN and RAHMAN [7] firstly treated the cutting force as a Fourier series, and took the effects of the mass eccentricity into consideration in the model of drilling shaft. Based on a similar idea, DENG and CHIN [8] took the cutting force on the cutting edge by harmonic functions. But they ignored the influence of hydrodynamic force. At present, nonlinear hydrodynamic forces of cutting fluid are normally simplified as analytical forms by using assumptions such as an approximate analytical hydrodynamic forces formulation or a second order lumped mass system with static fluid in the model of drilling shaft system [9-10]. Such simplified models do not accurately represent the practical drilling shaft system. Drilling shaft system as a rotating machine is a typical nonlinear dynamic system and hence nonlinear hydrodynamic forces of cutting fluid do not have analytical formulation in fact.

According to preceding problems, an isoparametric finite element method (FEM) was used to solve variational constraint problem with Reynolds boundary arising in cutting fluid for practical drilling shaft system in copper stave deep hole drilling. A perturbance equation can be obtained directly. Consequently, nonlinear hydrodynamic forces and their Jacobian matrices needed at every step of dynamic integration  and iteration were calculated simultaneously, and the

compatible accuracy was obtained. Then, the Newton shooting procedure was recompiled. The period took part in the iteration procedure of the shooting method as a parameter, and thus the periodic trajectories and the period of the drilling shaft system were determined rapidly. Based on the above analysis, the local stability and bifurcation behaviors of periodic motion were analyzed by the Floquet theory.

2 System equation

Fig.1 schematically represents a drilling shaft system, where the drill shaft is considered as a lumped mass clamped at the shaft driver while the workpiece is fastened at its end. Hence, the motion equations of the drilling shaft can be written as follows:

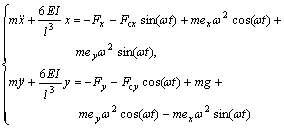 (1)

where m is half of the mass of the drilling shaft; E and I are elastic modulus and moment of inertia; l and l_c are the length of the drilling shaft and the drilling depth, respectively; -F_x and -F_y are nonlinear hydrodynamic forces of cutting fluid in x and y directions; -F_cx and -F_cy are the fluctuations of cutting force in x and y directions; g is the acceleration of gravity; e_x and e_y are mass eccentricities of the drilling shaft in x and y directions; ω is the rotating angular speed of the drilling shaft.

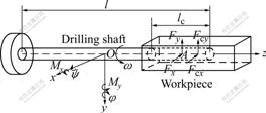
Fig.1 Schematic diagram of drilling shaft system

When state variables X=(x, y, 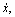 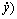^T=(X₁, X₂, X₃, X₄)^T are introduced, the corresponding system equation in state space is written as

   (2)

3 Nonlinear hydrodynamic forces of cutting fluid and their Jacobian matrices

Nonlinear hydrodynamic forces and their Jacobian matrices are estimated, which are needed at every step of iterative process when the drilling shaft trajectories of Eqn.(1) are solved. Compatible accuracy of nonlinear hydrodynamic forces and their Jacobian matrices affects not only the convergence of the shooting method solving periodic trajectories, but also analysis of stability and bifurcation of periodic trajectories [11]. In this work, based on FEM, variational constraint approach is introduced to solve variational inequalities with Reynolds boundary arising in cutting fluid. Since nonlinear hydrodynamic forces are the functions of displacements and velocities of the center of the drilling shaft, differential equations are used for this calculation.

The Reynolds equation is equivalent to the following discrete form of variational inequalities [12-13] arising in cutting fluid to satisfy the finite length drilling shaft (dimensionless):

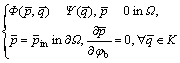                 (3)

where 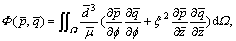  and

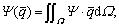
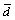  is the cutting fluid thickness

between the drilling shaft and deep hole surface, dimensionless,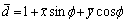;  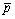is the cutting fluid pressure, dimensionless;  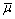is the dynamic viscosity of cutting fluid, dimensionless;  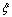is the ratio of diameter to length; 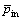is the pressure of cutting fluid, dimensionless;  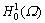is the Sobolev space; is the restricted, symmetric, and elliptical bilinear functional on 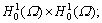 is the linear function; φ_b is the angle between the connection line of the eccentric angle with the center of the drilling shaft and intersection curve of cavitation field with no cavitation field of cutting fluid film (the intersection curve changes with the change of perturbation of drilling shaft displacements and velocities), dimensionless; K=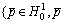≥0 in Ω}; Ω is the cutting fluid field of the round hole; and ?Ω is the boundary of Ω.

Fig.2 shows the coordinate of round hole for calculation, where  (dimensionless) is the angle between the negative direction of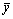axis and the cutting fluid film location; θ is the eccentric angle (dimensionless); φ is the angle between the connection line of the eccentric angle with the center of drilling shaft and cutting fluid location (dimensionless); G is the weight of drilling shaft (dimensionless); and  is the rotating angular speed of drilling shaft (dimensionless).

Fig.2 Coordinate of round hole for calculation

By using the eight-node isoparametric FEM, the distribution of pressures of nodal points in cutting fluid field is solved. Function 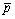 can be expressed as

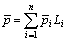                                 (4)

where   is the distribution of pressures of nodal points in cutting fluid field, dimensionless; L_i is interpolation function of the finite element.

Substituting Eqn.(4) into Eqn.(3) and introducing constraint give n-order discrete equation:

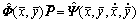                      (5)

where 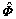  is the sparse, banded, and symmetric matrix with the first and the second constraint condition;  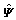is the column vector with the first and the second constraint condition.

Since the nonlinear hydrodynamic forces of cutting fluid are the functions of dynamic positions of the center of the drilling shaft, nonlinear hydrodynamic forces 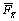 and 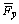 (dimensionless) can be obtained by integrating dynamic distribution of pressure:

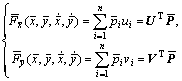                (6)

where

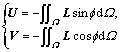                         (7)

U and V are constant column vectors. The Jacobian matrices of hydrodynamic forces 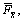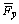, with respect to drilling shaft displacement 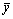  and velocities 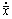,  can be written as

          (8)

(,

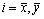where 

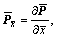
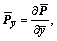
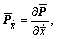
Taking partial derivatives of Eqn.(5) with respect to 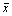, , 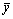, 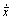and , gives perturbation equation

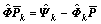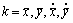 ()               (9)

The components of matrix 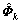 and vector  can be written as follows:

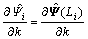
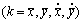          (10)

Substituting 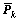 into Eqn.(8), Jacobian matrices of the nonlinear hydrodynamic forces can be obtained. It is evident that Eqn.(9) does not need to be recomputed because it resembles Eqn.(7). Eqn.(9) can be obtained from Eqns.(5), (7) and (10) when  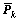is calculated, because Eqns.(5) and (9) have the same coefficient matrix 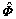. It is evident that Jacobian matrices of the nonlinear hydrodynamic forces are obtained when the hydrodynamic forces are calculated. Therefore, the accuracy and reliability of the analysis of nonlinear hydrodynamic forces are ensured, and the computing work spent on the Jacobian matrices is much less than that spent on the nonlinear hydrodynamic forces. After calculating the nonlinear hydrodynamic forces and Jacobian matrices of round hole (shown in Fig.2), nonlinear hydrodynamic forces and Jacobian matrices of slot hole can be estimated according to the characteristics of slot hole. O₁ and O₂ are the centers of the left round hole and the right round hole, respectively, as shown in Fig.3.

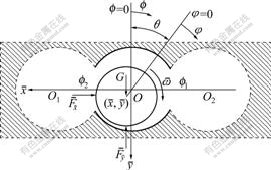
Fig.3 Coordinate of slot hole for calculation

4 Periodic trajectories and its period of drilling shaft system

The ordinary shooting method is suitable only for solving the periodic trajectories with the given period or the periods with the given periodic trajectories. Periodic trajectories and the period of the system cannot be calculated simultaneously. To overcome the above shortcomings, the shooting procedure is recompiled; the period takes part in the iteration procedure of the shooting method as a parameter. The increment value changed in the iteration procedure is selected by using the optimization method, and then the periodic trajectories and the period of the system are determined rapidly.

In order to show period T explicitly in the equation, we transform the system in Eqn.(2) into Eqn.(11) by using t=Tτ and then

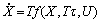
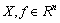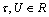and        (11)

where  U is the design parameter of drilling shaft system and T is the original period of the system in Eqn.(2). The period of the periodic trajectories of the system in Eqn.(11) is changed to 1. We choose the initial condition as 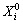 and 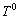(i=1, 2, …, n). Using the initial condition, we integrate the system in Eqn.(11) from τ=0 to τ=1. A periodic trajectory T is found if the following criterion is satisfied.

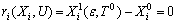                (12)

In order to obtain the iteration increment for the iteration process, we expand r into a Taylor series near to ε and T⁰, and retain the linear terms only:

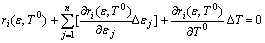
(i=1, 2, …, n)                           (13)

From Eqn.(12), we find the partial derivative of r_i with respect to ε_j and T⁰. The following formula can then be obtained:

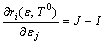(i=1, 2, …, n; j=1, 2, …, n)  (14)

where   and I is the Kronecker symbol.

 (i=1, 2, …, n)         (15)

By deriving the partial derivative of Eqn.(11) with respect to ε_j and T⁰, and let 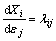, , 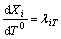then the following formula can be obtained:

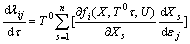
(i=1, 2, …, n; j=1, 2, …, n)              (16)

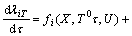
    (i=1, 2, …, n)                   (17)

By combining Eqns.(16) and (17), an initial value problem of an ordinary differential equation is formed. The initial conditions  and 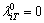 in these equations can be discovered by means of the selection of By using the initial condition mentioned above to integrate Eqns.(16) and (17) from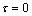to     τ = 1, we can obtain  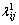and 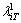. These are the values

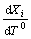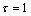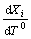of and at . We substitute the obtained solution of  and  at 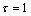 into Eqns.(14) and (15) separately. Then, the values of and 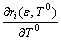can be obtained. By substituting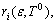  and 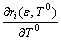 into Eqn.(13), a set of the

n-order linear equations with n+1 variables will be formed. In order to solve Δε₁, Δε₂, …, Δε_n and ΔT from Eqn.(13), one variable must be fixed. In r_i, the fact that r_k is the least means that the initial value of x_k selected is the closest to that of the actual periodic trajectories of the system. Therefore, we choose the minimum x_k to be fixed at the next iterative process. If ΔT in r_i is the minimum, the column corresponding to T cannot be deleted because period T of the periodic trajectories of the system is certain. After solving for the values, we let 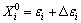 and 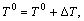 and repeat this procedure until the precision required is satisfied. Then, we make the contrary transform 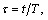and the periodic trajectories of the system in Eqn.(2) and its period can, thus, be obtained.

5 Results and discussion

A computer program was developed to compute the nonlinear dynamic behaviors of a drilling shaft system with slot hole layout (shown in Fig.4). In deep hole drilling process, the effect of fluctuation of cutting force is one of the important factors that influence the dynamic characteristic of drilling shaft system [14-15]. The fluctuation value of cutting force is 0.08 kN in this work. In experiment process, the stiffness of drilling shaft, the flow rate of cutting fluid, the temperature and so on cannot be under precise control. Therefore, according to actual experimental conditions, we satisfy the experimental requirements furthest. The parameters of the drilling shaft system are as follows. The length l is  1 250 mm; the inner diameter is 26 mm, and the external diameter is 34 mm. The material of drilling shaft is high strength alloy steel with the density of 7.87×10³ kg/m³. The dynamic viscosity of cutting fluid is 0.026 Pa?s. The pressure of cutting fluid is 2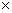10⁶ Pa. Take drilling depth as l_c=150 mm, diameter of drilling hole as 36 mm, hole intersection angle as α₁=α₂=13.57?, intersection length as τ₁ = τ₂ = 0.5 mm, rotating speed as n=1 256-1 413 r/min, and axial feed rate as 15 mm/min. The experiments are carried out at high speeds of rotation and minor feed rate in order to overcome the resistance of the workpiece. In experimental setup as shown in Fig.5, the eddy current sensors were located at 257 mm from the drilling tool along with x and y directions. Certainly, the results of theoretical calculation and experimental pickups are different. However, it is necessary for us to study whether the possibility and tendency of the theoretical calculation are consistent with the experiment results under different parameters [16].

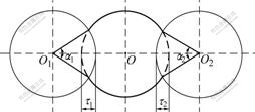
Fig.4 Layout of slot hole (α_i is intersection angle, τ_i is intersection length)

Taking rotating speed as n=1 256 r/min, eccentricity as e＝0 μm, the results of theoretical calculation and experimental pickups are shown in Fig.6. Based on Floquet theory [17], the module of the leading Floquet multiplier is a pair of complex conjugate eigenvalue,

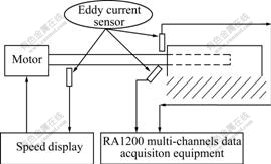
Fig.5 Schematic presentation of experimental setup

and then the system is almost periodic bifurcation. Experimental results prove that the movement trajectory of the drilling shaft is almost a periodic motion. Under different rotating speeds, the results of theoretical calculation and experimental pickups are shown in Figs.7 and 8. The movement trajectories of the drilling shaft gradually appear as periodic characteristics with the increase of rotating speed. At rotating speeds of 1 384 and 1 413 r/min, the modules of the leading Floquet multiplier of 1.025 8 (the leading Floquet multiplier  -1.025 8) and 0.982 1 are calculated by Floquet theory, respectively. The results of theoretical calculation present that the movement trajectories of the drilling shaft corresponding to rotating speed are period-doubling solution and stable periodic solution, respectively. When the rotational speed increases from 1 256 to 1 413 r/min, the whirl diameter increases gradually, as shown in Figs.6-8.

Taking rotating speed as n=1 328 r/min, eccentricity as e=1.425 and 7.285 μm, it is noteworthy that the whirl diameter decreases significantly with the increase of the mass eccentricity, as shown in Figs.9 and 10. This shows that the mass eccentricity can inhibit the whirling motion of drilling shaft to some extent.

Fig.6 Movement trajectory of center of drilling shaft at n=1 256 r/min and e=0 μm: (a) Results of theoretical calculation; (b) Results of experimental pickups

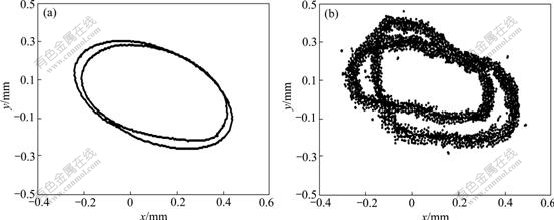
Fig.7 Movement trajectory of center of drilling shaft at n=1 384 r/min and e=0 μm: (a) Results of theoretical calculation; (b) Results of experimental pickups

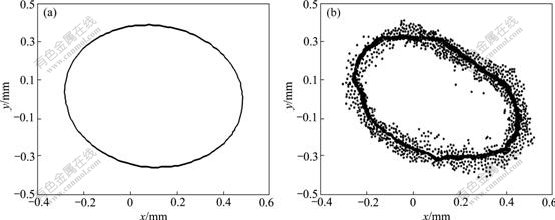
Fig.8 Movement trajectory of center of drilling shaft at n=1 413 r/min and e=0 μm: (a) Results of theoretical calculation; (b) Results of experimental pickups

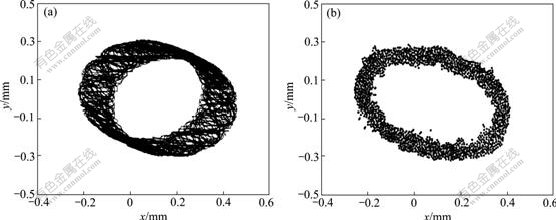
Fig.9 Movement trajectory of center of drilling shaft at n=1 328 r/min and e=1.425 μm: (a) Results of theoretical calculation;      (b) Results of experimental pickups

6 Conclusions

(1) A mathematical approach is developed to calculate the nonlinear hydrodynamic forces of cutting fluid and their Jacobian matrices of compatible accuracy simultaneously.

(2) The primary characteristic of new shooting method is that the solving process includes the process of determining the periodic trajectory of drilling shaft and its period.

(3) By combining theories with experiment, the

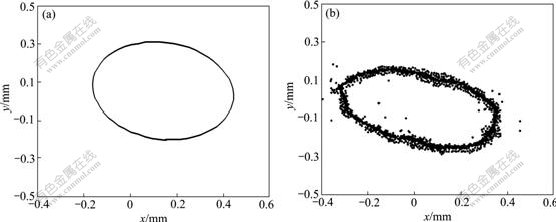
Fig.10 Movement trajectory of center of drilling shaft at n=1 328 r/min and e=7.285 μm: (a) Results of theoretical calculation;     (b) Results of experimental pickups

correctness and effectiveness of the above methods are verified by using the Floquet theory. The whirling diameter of drilling shaft increases gradually with the increase of rotating speed, and the whirling diameter of drilling shaft decreases significantly with the increase of mass eccentricity. The results indicate that the research of this work has an important influence on the quantitative control of the motion of drilling shaft in copper stave deep hole drilling.

References

[1] HELENBROOK R G. Water requirements for blast furnace copper staves [J]. Iron and Steel Maker, 2000, 27(6): 45-51.

[2] EMA S, MARUI E. Theoretical analysis on chatter vibration in drilling and its suppression [J]. Journal of Materials Processing Technology, 2003, 138: 572-578.

[3] EMA S, FUJII H, MARUI E. Whirling vibration in drilling—Part 1. Cause of vibration and role of chisel edge [J]. Journal of Engineering for Industry, 1986, 108: 157–162.

[4] EMA S, FUJII H, MARUI E. Whirling vibration in drilling—Part 2. Influence of drill geometries, particularly of the drill flank, on the initiation of vibration [J]. Journal of Engineering for Industry, 1986, 108: 163-168.

[5] EMA S, FUJII H, MARUI E. Whirling vibration in drilling—Part 3. Vibration analysis in drilling workpiece with a pilot hole [J]. ASME Journal of Engineering for Industry, 1988, 110: 315-321.

[6] BATZER S, GOUSKOV A, VORNOV S. Modeling vibratory drilling dynamics [J]. Journal of Vibration and Acoustics, 2001, 123(4): 435-443.

[7] MATIN M A, RAHMAN M. Analysis of the cutting process of a cylindrical workpiece clamped by a three-jaw chuck [J]. Journal of Engineering for Industry, 1988, 110: 326-332.

[8] DENG C S, CHIN J H. Roundness errors in BTA drilling and a model of waviness and lobing caused by resonant forced vibrations of its long drill shaft [J]. Journal of Manufacturing Science and Engineering, 2004, 126: 524-534.

[9] HU Zhan-qi, ZHAO Wu, MIAO Lei. Research on vortex motion of BTA drilling shaft caused by hydro-force [J]. Chinese Journal of Mechanical Engineering, 2005, 41(1): 230-233. (in Chinese)

[10] PERNG Y L, CHIN J H. Theoretical and experimental investigations on the spinning BTA deep-hole drill shafts containing fluids and subject to axial forces [J]. International Journal of Mechanical Sciences, 1999, 41(11): 1301-1322.

[11] SHI Zhang-ming, E Jia-qiang, LIU Chun-yang, MEI Chi, ZHANG Quan, ZHOU Ying-qi. Numerical simulation of flow phenomena and optimum operation of tundish [J]. Journal of Central South of Technology, 2003, 10(2): 155-158.

[12] PARKER T S, CHUA L O. Practical numerical algorithms for chaotic system [M]. New York: Springer-Verlag, 1989.

[13] KINDERLENHRER D, STANPACCHINA G. An introduction to variational inequalities and their application [M]. New York: Academy Press, 1980.

[14] HUSSIEN M A W, RAMA B B, KUDRET D. Whirling vibration in boring trepanning association deep hole boring process: Analytical and experimental investigations [J]. Journal of Manufacturing Science and Engineering, 2007, 129(1): 48-62.

[15] KOVACIC I. Chatter vibrations in cutting-theoretical approach [J]. Facta Universitatis: Mechanical Engineering, 1998, 1(5): 581-593.

[16] LI Ke-an, XIAO Han, CUI Rong-fan. Bifurcation control of nonlinear oscillator in primary and secondary resonance [J]. Journal of Central South of Technology, 2007, 14(6): 826-831.

[17] SEYDEL R. From equilibrium to chaos bifurcation and stability [M]. New York: Elsevier, 1988.

(Edited by YANG You-ping)

Foundation item: Project(2007CB707706) supported by the Major State Basic Research Development Program of China; Projects(2007E213, 2007E203) supported by the Natural Science Foundation of Shaanxi Province, China

Received date: 2008-08-26; Accepted date: 2008-11-27

Corresponding author: KONG Ling-fei, Doctoral candidate; Tel: +86-13072931712; E-mail: lingfei.kong@163.com