侧喷加热铝材退火炉内流场与温度场数值模拟
李建平，王伯长，刘涛，毛大恒
(中南大学 机电工程学院，现代复杂装备设计与极端制造教育部重点实验室，湖南 长沙 410083)
摘 要：采用热传导模拟实验研究铝卷层与层之间接触热阻对铝材退火的影响。根据实验结果分析，改变现有径向加热铝材退火炉内循环空气的流动方向，采用轴向对流换热方式，设计侧喷加热铝材退火炉，建立侧喷加热铝材退火炉三维仿真模型。利用CFD软件FLUENT，采用标准k-ε湍流模型，对侧喷加热铝材退火炉内气体流动和传热问题进行数值模拟研究。研究结果表明：与径向传热方式相比，轴向传热方式退火速度快，铝卷芯部与外部表面之间的温差小；侧喷加热铝材退火炉内气体流动顺畅，对流换热均匀，炉温温差控制在-1~1 K，满足退火工艺对炉温均匀性的要求。
关键词：侧喷加热铝材退火炉；流场；对流换热；温度场；数值模拟
中图分类号：TG155.1+2；O357.5+3 文献标志码：A 文章编号：1672-7207(2010)01-0166-06
Numerical simulation of flow and temperature field in side-blown aluminum annealing furnace
LI Jian-ping, WANG Bo-chang, LIU Tao, MAO Da-heng
(Key Laboratory of Design for Modern Complex Equipment and Extreme Manufacturing, Ministry of Education,
School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
Abstract: The effect of thermal contact resistance between aluminum coil for aluminum annealing was investigated by simulation experiment of heat conduction. Based on this interpretation, side-blown aluminum annealing furnace was designed by changing flow direction of air cycle in furnace and adopting axial convection heat transfer. Simulation model of side-blown aluminum annealing furnace was established, numerical simulation of turbulent flow and heat transfer in furnace were done by using CFD software i.e., FLUENT and standard k-ε turbulence model, flow and temperature fields in furnace were illustrated. The results show that, compared with radial heat transfer, the efficiency of annealing is higher and temperature difference between aluminum coil’s internal and external surface is small by using axial heat transfer. The flow in furnace is fluent, convection heat transfer is uniform, and the temperature difference of furnace gas is -1 to 1 K and can satisfy the annealing technology’s desire about the uniformity of furnace gas’s temperature.
Key words: side-blown aluminum annealing furnace; flow field; convection heat transfer; temperature field; numerical simulation
退火是铝材生产过程中的重要工序。目前，国内生产使用的铝材退火炉基本上采用炉体顶部引风底部进风的形式，而铝卷水平地放在料架上，这样导致炉膛内热气流的流动方向为铝卷的直径方向，形成了铝卷与热气流之间的径向对流换热[1-2]。由于铝卷层与层之间有间隙以及铝卷轧制过程中形成油膜，这样，铝卷层与层之间存在接触热阻[3-6]，导致铝卷与热气流之间的对流换热效率低，铝卷表面与芯部温差大，严重影响铝卷的退火效率和质量。而在国外已经生产使用的侧喷加热式铝材退火炉[7]，大型退火炉的传热效率达到70%以上，明显高于国内大型铝卷退火炉的传热效率[8]。通过对铝箔板叠加而成的长方体试件所做的热传导实验也发现：在同样的试件、温度源和保温效果下，仅仅只是改变传热方式，即试件由平面传热方式改为端面传热方式，退火时间明显减少。因此，改变炉膛内空气循环流动的方向，使热空气和铝卷之间进行轴向的对流换热，实现金属的直接传热，即研制出侧喷加热铝材退火炉对于提高铝卷的退火效率和质量，节约能源具有重要意义。炉膛内气体流动和对流换热状况是影响铝材退火质量和生产效率的关键因 素[9]，为了设计出性能优越的侧喷加热铝材退火炉，就必须了解退火时炉膛内空气流动规律和温度分布规律。由于侧喷加热铝材退火炉内结构复杂，流场和温度场的测量十分困难，且不能全面揭示流动和传热规律。数值模拟的方法已广泛用于各种炉窑的研究[10-13]，在此，本文作者利用CFD软件FLUENT对侧喷加热铝材退火炉内气体流动和传热问题进行数值模拟研究，得到炉膛内空气流动规律和温度分布规律，以便为侧喷射加热铝材退火炉的设计与研究提供理论 依据。
1 热传导模拟实验
铝卷层与层之间的接触热阻是影响铝卷径向导热的最重要因素，也是研究传热效率的重要参数之一。为了反映接触热阻对铝材退火效率的影响，利用铝箔板叠加而成的长方体试件分别进行平面传热及端面传热实验，实验装置如图1所示。图中数字1~6为6个温度测试点，其中：测试点“1”用于估测热源的温度；“2”与“3”分别用于测试距离热源为82 mm和134 mm这2点的温度；“4~6”用于测试实验装置内气体的温度。利用热电偶和无纸记录仪对6个测温点进行数据采集，每5 min记录1次结果。
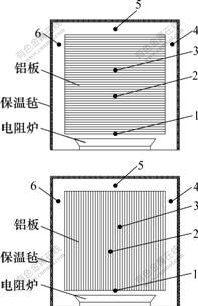
(a) 平面传热；(b) 端面传热
图1 实验装置示意图
Fig.1 Schematic diagram of experimental facility
图2和图3所示分别为平面传热和端面传热方式下离热源82 mm和134 mm 2个测温点的温度对比曲线。可以看出：在使用相同功率的电阻炉进行加热，并且维持实验装置内气体温度基本一致的情况下，在同一时刻、同一测试点，端面传热方式的温度比平面传热方式的温度高，也就是说，达到相同退火温度时，端面传热方式所需时间比平面传热方式所花时间少，并且距离热源越远，这种差别越明显，在82 mm处温差最大达到50 ℃，最后维持在20 ℃左右，达到相同退火温度时，端面传热方式所需时间比平面传热方式缩短10%左右；而在134 mm处温差最大达到80 ℃，最后维持在60 ℃左右，达到相同退火温度时端面传热方式所需时间比平面传热方式所花时间缩短20%左右。图4所示为相同传热方式下离热源82 mm与134 mm 2个测温点之间的温差对比曲线。从图4可以看出：使用平面传热方式时，2点之间的温差最高达到50 ℃左右；而使用端面传热方式时，2点之间的温差维持在0 ℃左右，也就是说2点的温度基本一致，最多相差2~3 ℃。
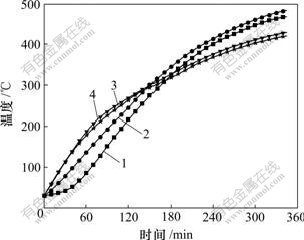
1—平面传热时离热源82 mm处温度曲线；2—端面传热时离热源82 mm处温度曲线；3—平面传热炉温曲线；4—端面传热炉温曲线
图2 离热源82 mm处温度对比曲线
Fig.2 Comparison of temperature on position 82 mm from energy resource
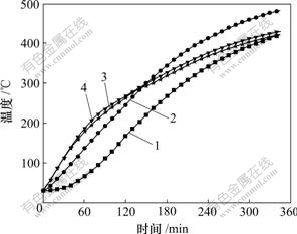
1—平面传热时离热源134 mm处温度曲线；2—端面传热时离热源134 mm处温度曲线；3—平面传热炉温曲线；4—端面传热炉温曲线
图3 134 mm处温度对比曲线
Fig.3 Comparison of temperature on position 134 mm from energy resource
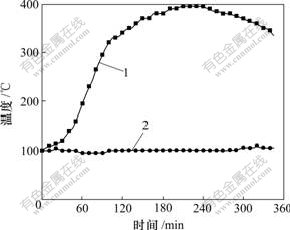
1—平面传热时2点之间温差曲线；2—端面传热时2点之间温差曲线
图4 温差对比曲线
Fig.4 Comparison of temperature difference
2 侧喷加热铝材退火炉
通过模拟实验结果可知：由于铝板层与层之间存在接触热阻，严重影响了热量在铝板之间的传递，从而使得铝板退火效率低，不同位置间温差大。而采用端面传热的方式可以实现金属的直接传热，避免接触热阻产生的影响，提高退火效率，减少不同位置间的温差。将这实验原理及结果运用于铝材退火炉，对现有的径向加热铝材退火炉进行改进，设计侧喷加热铝材退火炉可有效地提高铝卷的退火效率和质量，节约能源。
侧喷加热铝材退火炉由箱式炉体、导流装置、循环系统、排烟系统、加热元件、炉门、炉门升降机构及其压紧装置、炉门密封、冷却水系统等组成。循环系统采用低压大风量轴流风机，使炉内热风在导流装置的作用下定向循环，同时，增强了炉内的对流换热，提高炉内温度上升速度，也使得炉内温度均匀。侧喷加热铝材退火炉内空气循环示意图如图5所示。
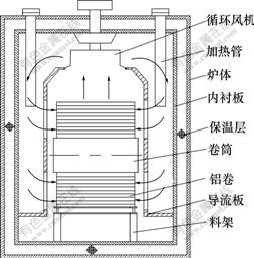
图5 炉内空气循环示意图
Fig.5 Schematic diagram of air cycle in furnace
3 炉内气体流动与换热计算模型
3.1 计算区域及网格划分
以箱式炉体以及由其包围的流体空间为计算区域，利用专用处理软件GAMBIT建立三维立体模型，并进行网格划分。鉴于流体区域模型比较复杂，采用Tet/Hybfid单元、TGfid混合网格划分网格；箱式炉体、导流装置、炉门结构简单，采用Hex单元、Map结构网格划分网格；加热管采用Hex/Wedge单元、Cooper非结构网格划分网格，最后，模型的网格总数为1 191 305。网格划分结果如图6所示。
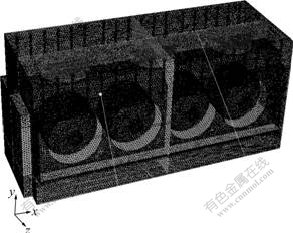
图6 网格结构图
Fig.6 Structural diagram of grid
3.2 基本控制方程
流体流动遵循物理守恒定律。应用CFD软件求解流动及换热问题时，控制方程包括连续性方程、动量方程、能量方程，这些方程的通用表达形式为：
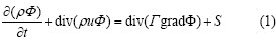
式中：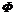
为广义变量，如温度、浓度等；u为速度；
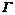为广义扩散系数；S为广义源项。式(1)中，从左至右各项依次为瞬态项、对流项、扩散项和源项。
3.3 湍流模型
在炉膛内部空气处于湍流状态，湍流模型采用工程上广泛使用的标准k-ε模型[14-16]。标准k-ε模型通过湍动能k和湍动能耗散率ε表示湍动黏度μt，即
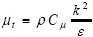
再通过湍动黏度求解Reynolds应力及Navier-Stokes方程。在标准k-ε模型中，k和ε是2个基本未知量，与之相对应的输运方程为：
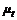为湍流涡团黏性系数；Gk为平均速度梯度引起的湍动能k的产生项；ρ为气体(固体)密度；k为热导率；ε为气体湍流入动能耗散率；ui为气体速度分量；C1ε，C2ε，Cμ，σk和σε均为模型常数，根据Launder等的推荐值以及后来的实验验证[17]，它们的取值为：C1ε= 1.44，C2ε=1.92，Cμ=0.09，σk=1.0，σε=1.3。
在近壁区，由于湍流发展不充分，不适合采用标准k-ε模型进行计算。为了解决近壁区内的流动计算，采用壁面函数法，其方程为：
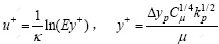
其中：u+和y+为2个无量纲的参数，分别表示速度和距离；kp为节点p的湍动能；?yp为节点到壁面的距离；μ为流体的动力黏度；E为与粗糙度有关的常数，对于光滑壁面，E=9.8。
3.4 边界条件
根据退火炉实际使用工况，炉体外部表面设置为辐射壁面条件；内部表面及导流板表面设置为对流换热壁面条件；炉体及内衬板、导流板的材料为1Cr13，密度为7.7 t/m3，比热容为460 J/(kg?K)，导热系数为24.2 W/(m?K)；保温层的材料为硅酸铝保温毡，密度为130 kg/m3，比热容为1.013 75 J/(g?K)，导热系数为0.057 W/(m?K)；加热管表面设置为等热流密度边界条件，热流密度为840 W/m2；炉内循环风机采用风扇边界条件，风机的额定转速为1 440 r/min，额定风量为148 000 m3/h，风压为500 Pa。
4 数值模拟结果与分析
选择有限体积法离散控制方程，采用QUICK格式和中心差分格式分别作为对流项和扩散项的离散格式；流场计算使用SIMPLE算法；能量方程和动量方程用二阶迎风格式离散；使用默认的松弛因子进行迭代计算，直到最终收敛为止。下面对流场和温度场的模拟结果进行分析。
4.1 流场模拟结果及分析
图7所示分别为平行炉体前面、底面、侧面3个截面的速度等值线图。
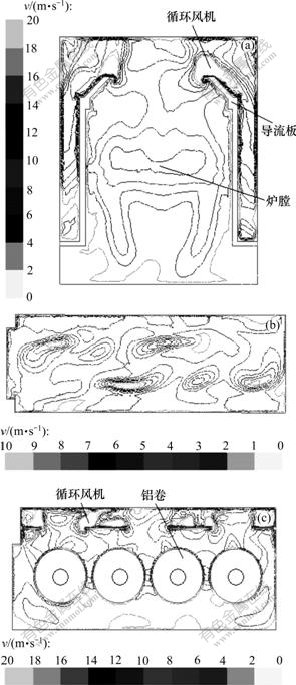
(a) 平行炉体前面的截面；(b) 平行炉体底面的截面；(c) 平行炉体侧面的截面
图7 不同截面的速度等值线
Fig.7 Velocity contours in different sections
从图7(a)可以看出：炉顶和循环风机之间的区域以及炉体两侧和导流板之间的区域速度较高，炉膛内风速为10 m/s左右，且速度等值线基本上呈对称分布；贴近炉体内表面的区域速度明显小于其他区域的速度，形成了湍流黏性底层，使得炉体内表面的对流换热强度减少。
从图7(b)可以看出：由于从两侧导流板进入炉膛的气体方向相反，产生了气体回流，形成了不同程度的循环气流。这种循环气体不仅可以改善炉内温度的均匀性，还可以加强热气流与铝卷之间的对流换热。
从图7(c)可以看出：采用轴向对流换热方式时，气体在导流板的引导下直接进入炉膛内，通过铝卷表面后转向炉体底部使得炉膛内气体的速度大于炉体底部气体的速度，这样，速度分布不仅加强了气体与铝卷之间的对流换热，同时，减少了炉体底部同外界的热散失。
4.2 温度场模拟结果及分析
图8所示分别为平行炉体前面的截面1.0 h后、平行炉体底面的截面2.0 h后、平行炉体侧面的截面1.5 h后的温度分布图。从图8可以得到：炉内的温差都可控制在-1~1 K内，能满足退火工艺对炉温均匀性的要求，这也说明改变铝材退火炉的加热方式并不会降低炉内温度场的均匀性，从而保证铝卷的退火质量。从图8(a)和8(b)可以看出：炉膛内温度基本一致，且炉膛内的温度高于炉体底部的温度，与炉体两侧的温度一致。这有利于加强炉膛内铝卷与空气之间的对流换热，同时减少炉体底部与外界的热散失。从图8(c)可以看出：炉门区域与炉膛后侧的温度与炉膛内的温度一致，克服了径向加热铝材退火炉内这2个区域温度低的不足。
(a) 平行炉体前面的截面(t=1.0 h)；(b) 平行炉体底面的截面(t=2.0 h)；(c) 平行炉体侧面的截面(t=1.5 h)
图8 不同截面的温度分布
Fig.8 Temperature distribution in different sections
5 结论
(1) 采用端面传热的方式可以实现金属的直接传热，避免接触热阻产生的影响，从而缩短退火时间，提高退火效率，同时也可以减少不同位置间的温差，提高退火质量。运用这个实验原理及结果，对现有的径向加热铝材退火炉进行改进，设计侧喷加热铝材退火炉。
(2) 采用侧喷加热方式时，从两侧导流板进入炉膛的气体在炉膛内形成了不同程度的循环气流。这种循环气体不仅可以提高炉内温度的均匀性，还可以加强热气流与铝卷之间的对流换热；同时，炉膛内气体的速度大于炉体底部气体的速度。
(3) 采用侧喷加热方式时，炉内气体温度基本一致，温差可控制在-1~1 K，能满足退火工艺对炉温均匀性的要求，这也说明改变铝材退火炉的加热方式并不会降低炉温的均匀性，从而保证铝材的退火质量。
参考文献：
[1] 李建平, 艾江波, 胡仕成, 等. 用ANSYS软件对铝材退火炉内铝卷温度场的数值模拟[J]. 金属热处理, 2008, 33(3): 97-100.
LI Jian-ping, AI Jiang-bo, HU Shi-cheng, et al. Numerical simulation of aluminum coil temperature field in annealing furnace by ANSYS software[J]. Heat Treatment of Metals, 2008, 33(3): 97-100.
[2] 李建平, 艾江波, 胡仕成. 铝材退火炉退火过程的传热分析[J]. 热加工工艺, 2007, 36(20): 76-78.
LI Jian-ping, AI Jiang-bo, HU Shi-cheng. Study on heat transfer in annealing process of aluminum annealing furnace[J]. Hot Working Technology, 2007, 36(20): 76-78.
[3] 殷晓静, Degiovanni A. 接触热阻的三维数学模型的研究(一):数学模型[J]. 北京科技大学学报, 1996, 18(4): 384-386.
YIN Xiao-jing, Degiovanni A. study of contact thermal resistance between two coaxial cylindrical layer (1): Mathematic model[J]. Journal of University of Science and Technology Beijing, 1996, 18(4): 384-386.
[4] Fieberg C, Kneer R. Determination of thermal contact resistance from transient temperature measurements[J]. International Journal of Heat and Mass Transfer, 2008, 51(5/6): 1017-1023.
[5] Majid B, Michael Y M, Richard C J. Thermal contact resistance at low contact pressure: Effect of elastic deformation[J]. International Journal of Heat and Mass Transfer, 2005, 48(16): 3284-3293.
[6] ZHANG Xin-xin, ZUO Yan, WU Wen-fei. Analytical and experimental study on radial equivalent thermal conductivity for steel coil heat transfer in HPH furnace[C]//Proceedings of the Twelfth International Heat Transfer Conferences. Grenoble, 2002: 18-23.
[7] Ross R H. Vertical air flow ingot pusher furnace: United States, 4676743[P]. 1987-06-30.
[8] Abe S I. Development of energy saving technology for continuous annealing furnace of stainless steel strip[C]//SEAISI Conference on Energy Utilization in the Iron and Steel Industry. Pasay: South East Asia Iron & Steel Inst, 1984: 14.
[9] 郭陵松. 铝箔退火炉流场与温度场数值模拟[D]. 长沙: 中南大学机电工程学院, 2006.
GUO Ling-song. Numerical simulation of flow and temperature field in aluminum annealing furnace[D]. Changsha: School of Mechanical and Electrical Engineering, Central South University, 2006.
[10] 高晖, 郭烈锦, 顾汉洋. 梭式窑空气动力模型中紊流流动与对流传热的数值模拟[J]. 硅酸盐学报, 2002, 30(5): 602-607.
GAO Hui, GUO Lie-jin, GU Han-yang. Numerical simulation of turbulent flow and convective heat transfer in air dynamic model of shuttle kiln[J]. Journal of the Chinese Ceramic Society, 2002, 30(5): 602-607.
[11] 肖友刚, 刘义伦, 马爱纯.回转窑窑壁非稳态传热模型及窑皮厚度优化[J]. 中国有色金属学报, 2006, 16(6): 1115-1119.
XIAO You-gang, LIU Yi-lun, MA Ai-chun. Transient heat transfer model of kiln wall and kiln crust thickness optimization[J]. The Chinese Journal of Nonferrous Metals, 2006, 16(6): 1115-1119.
[12] Veranth J M, Silcox G D, Pershing D W. Numerical modeling of the temperature distribution In a commercial hazardous waste slagging rotary kiln[J]. Environ Science Technology, 1997, 31(9): 2 534-2 539.
[13] Mastorakos E, Massias A, Tsakiroglou C D, et a1. CFD predictions for cement kilns including flame modelling, heat transfer and clinker chemistry[J]. Applied Mathematical Modelling, 1999, 23(1): 55-76.
[14] Jones W P, Launder B E. The prediction of laminarization with a two-equation model of turbulence[J]. International Journal of Heat and Mass Transfer, 1972, 15(2): 301-314.
[15] 陈祎, 罗永浩, 时章明, 等. 硬质合金烧结—热等静压炉的优化[J]. 中南大学学报: 自然科学版, 2007, 38(2): 320-325.
CHEN Yi, LUO Yong-hao, SHI Zhang-ming, et al. Optimization of cemented carbide sinter-HIP furnace[J]. Journal of Central South University: Science and Technology, 2007, 38(2): 320-325.
[16] Seeta R G, Vengadesan S. Performance of two equation turbulence models for prediction of flow and heat transfer over a wall mounted cube[J]. International Journal of Heat and Mass Transfer, 2008, 51(11/12): 2834-2846.
[17] Launder B E, Iacovides H. Computational fluid dynamics applied to internal gas-turbine blade cooling: A review[J]. International Journal of Heat and Fluid Flow, 1995, 16(6): 454-470.
收稿日期：2008-11-16；修回日期：2009-03-10
基金项目：国家教育部留学回国人员基金资助项目(76084)
通信作者：李建平(1952-)，男，湖南长沙人，博士，教授，博士生导师，从事材料热处理设备与工艺、温度控制与仿真研究；电话：0731-88830102；E-mail: rikennpei102@hotmail.com
(编辑 陈灿华)
