Trans. Nonferrous Met. Soc. China 23(2013) 1751-1760

Finite element analysis of quenching temperature field, residual stress and distortion in A357 aluminum alloy large complicated thin-wall workpieces

Xia-wei YANG^1,2, Jing-chuan ZHU¹,², Zhong-hong LAI^1,2, Yong LIU^1,2, Dong HE^1,2, Zhi-sheng NONG^1,2

1. National Key Laboratory for Precision Hot Processing of Metals, Harbin Institute of Technology, Harbin 150001, China;

2. School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China

Received 28 May 2012; accepted 9 October 2012

Abstract: The quenching processes of A357 aluminum alloy large complicated thin-wall workpieces were investigated by finite element method (FEM) simulation based on ABAQUS software. Heat transfer coefficients of different quenchants were accurately calculated by a traditional method of inverse heat transfer. The accurate heat transfer coefficients of different quenchants can ensure accuracy FEM results of temperature field of A357 alloy large complicated thin-wall workpieces during quenching. The quenchants of water, machine oil and 5%-UCON quenchant A were used. Quenching residual stress and distortion were investigated by considering the influence of quenchant and quenchant temperature. The maximum residual stress and distortion of quenched workpieces were predicted by using FEM simulation based on ABAQUS software.

Key words: A357 aluminum alloy; complicated thin-wall workpieces; finite element method (FEM) simulation; residual stress; distortion

1 Introduction

A357 alloy (Al-7Si-0.6Mg) is an important alloy that is widely applied in commercial Al-Si-Mg cast alloys, particularly in the aerospace, automotive industries and other applications because of its excellent castability, good corrosion resistance and high specific strength in the heat treated condition [1-3]. The thin-walled workpieces (e.g. frame, thin-walled beam, and wall panel) from this alloy have a wide range of applications in the aerospace industries. The thin-walled workpieces are routinely heat treated to the T6 state to obtain adequate mechanical properties. The T6 heat treatment is made up of solution heat treatment, quenching and age hardening. Rapid cooling during quenching of A357 alloy can be helpful to inhibiting the formation of Mg-Si precipitates [4]. But residual stresses caused by rapid cooling often cause excessive distortion of workpieces and influence material’s mechanical properties such as stress corrosion and fatigue life [5-8]. Therefore, it is very necessary to investigate the residual stresses of A357 alloy parts after quenching. Numerical simulation of quenching process of workpieces has been widely studied since experimental investigation often leads to very high costs and spends a lot of time. Residual stresses of aluminum alloy workpieces during quenching are usually investigated by using FEM model [9-12] and experimental methods such as X-ray [13,14], hole drilling [15,16]. TODINOV [17] studied the influence of the martensitic start temperature and the martensitic transformation temperature interval on residual stresses from quenching. LI et al [18] simulated the quenching process by using FEM method, and then compared the experimental hardness with FEM results. The heat transfer coefficient is an important factor for quenching process of workpieces, so it must be taken into account for prediction of quenching residual stresses [19]. The inverse heat transfer method was widely adopted in the field of calculating the heat transfer coefficient of quenching medium [20,21]. Because this approach is a traditional method, a detailed description can not give information to calculate the heat transfer coefficient of quenching medium but can directly give the results of calculation. Water and machine oil are the quenchants most commonly used in the application of industry production. UCON quenchant is an aqueous PAG (polyalkyene glycol) quenchant. UCON quenchant A (shorted as UCON A) is an effective quenching agent for aluminum alloys. The heat transfer coefficients of water, machine oil and UCON A are determined by their temperatures. Comparisons of different temperatures of different quenchants in quenching process of aluminum parts are of great usefulness to control residual stresses and distortion. Therefore, in order to calculate the quenching process and to predict the residual stress of quenching parts, the accurate calculation of heat transfer coefficient of different quenchants at different temperatures will be very valuable for this study.

In this work, the study combining FEM analysis with experimental methods was performed to investigate the quenching process and to predict the residual stress of A357 alloy large complicated thin-wall workpieces. Cooling curves of Inconel 600 probe in different quenchants at different temperatures were obtained according to international standard ISO9950. Based on the cooling curves of probe, the heat transfer coefficients at different water temperatures were solved by an inverse heat transfer method. The accuracy of heat transfer coefficients is testified by comparison of the experimental temperature of probe inner point and the simulated data. The quenching process of A357 alloy large thin-wall workpieces and the distribution/ magnitude of residual stress of quenched thin-wall workpieces are simulated by using ABAQUS CAE software. Finally, the influence of quenchant and quenchant temperature on the residual stress and distortion of A357 quenched thin-wall workpieces are investigated by using FEM simulation method.

2 Experimental

The main chemical composition in mass fraction of commercial A357 aluminum alloy used in the present investigation is as follows: 6.83%Si, 0.51%Mg, 0.18%Ti, 0.04%Cu, 0.03%Fe, 0.02%Be and Al balance. The quenchants used in this work are water, machine oil and 5%-UCON A (volume fraction: φ_UCON-A=5% and φ_H2O= 95%). According to international standard ISO9950, an instrument was manufactured to record the cooling curves and the cooling rate curves of quenchants.  Figure 1 shows the schematic diagram of probe of this instrument used in this investigation. An Inconel alloy 600 cylindrical probe (d12.5 mm×L60 mm) was heated to a temperature of 860 °C. Then, it was quenched in water, machine oil and 5%-UCON A, respectively. The temperatures of water were 25, 45, 60 and 80 °C, respectively. The temperatures of machine oil and 5%-UCON A were 25, 45 and 60 °C, respectively. Table 1 shows the quenchants and their temperatures used in this investigation.

Fig. 1 Schematic diagram of probe (Unit: mm)

Table 1 Quenchants used in this work

During the quenching process, the change of temperature in probe inner point (point A in Fig. 1) with time can be measured with measurement-recording system. After obtaining the temperature—time curve of inner point A, the temperature history and the heat flux of the probe outer point B can be calculated by the inverse heat transfer method. Then the heat transfer coefficients of different quenchants at different temperatures can be calculated by Newton’s law of cooling.

3 FEM model of quenching process

3.1 FEM model

In this study, the finite element method is applied to simulating quenching process of A357 alloy large complicated thin-wall workpiece. Figure 2 shows three-dimensional graphics, finite element mesh generation and dimensions of A357 alloy large complicated thin-wall workpiece. As can be shown in Fig. 2(a), the structural characteristics of the large complicated thin-wall workpiece is as follows: stiffening plates along radial and axial directions, two visual windows, four bosses along radial direction on the bottom side and four grooves on the top side. The schematic of thin-wall workpiece with dimensions is shown in Fig. 2(b). The wall thickness, the height, the diameter of bottom face and the cone angle of thin-wall workpiece are 8 mm, 700 mm, 600 mm and 3°, respectively. The shape of large complicated thin-wall workpiece was take into account, so quarter workpiece was adopted in this study. The simplification of model and mesh generation are shown in Fig. 2(c). The total numbers of nodes and elements of the simplified model are 53934 and 36767, respectively, as shown in Fig. 2(c). Type DC3D8 and C3D8R in ABAQUS were adopted in the simulations for heat transfer analysis and stress/deformation analysis, respectively. The yield strength at different temperatures for A357 alloy can be obtained from Refs. [22,23]. The material properties used in this study can be obtained from Refs. [24,25].

Fig. 2 Three-dimensional graphics, mesh generation and dimensions of A357 aluminum alloy large complicated thin-wall workpiece

3.2 Mathematical model

The heat conduction equation describes the distribution of heat in a given region over time. According to the Fourier model and the first law of thermodynamics, the equation can be described as

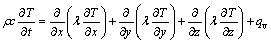  (1)

where r, c and l denote density, constant pressure specific heat and heat conductivity, respectively; T and t are thermodynamic temperature and time, respectively; q_v is the latent heat of phase transformation. Because the purpose of quenching A357 alloy is to inhibit the formation of Mg-Si precipitates, the value of q_v is set to be zero.

The initial condition is an initial value problem. In this work, initial condition is the initial temperature of quenching workpieces. The equation of initial condition at time t = 0 is as follows:

T|_t=0=T₀(x,y,z)                              (2)

where T₀(x, y, z) is the initial temperature function.

Boundary condition is the way of heat transfer between quenching workpieces and medium. It is given by

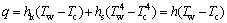        (3)

where q, h_k, h_s and h are thermal flux, convection coefficient, radiation coefficient and total heat transfer coefficient, respectively; T_w and T_c are the temperature of boundary and the temperature of ambience, respectively. The temperature and strain fields were calculated by thermo-mechanical coupled simulation with ABAQUS software. The numerical simulations of stress and strain fields were carried out with the same finite element mesh used in the thermal analysis, except for the element type and different boundary conditions. Because the distortion of the quenched workpiece is very small, the heat produced by deformation is small in the quenching operation. So, the influence of the stress field on temperature field cannot be taken into account. Therefore, a sequential analysis of coupled thermal-stress was employed in this investigation. The mechanical analysis was carried out with the temperature history computed in the thermal analysis as the input information. Using a small deformation theory, the total strain (e) can be additively decomposed into five components as

                  (4)

where e^e, e^p , e^th, e_△^V and e^tr are the elastic strain tensor, the plastic strain tensor, the thermal plastic strain tensor, the volumetric strain tensor and the transformation induced plastic strain tensor, respectively.

Because the purpose of quenching A357 alloy is to limit the happening of phase transition, the value of ε^tr is set to zero. So, the strain increment can be given by

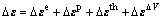                (5)

where Δε^e, Δε^p, Δε^th and Δε^ΔV are elastic strain increment, plastic strain increment, thermal plastic strain increment and volumetric strain increment, respectively.

3.3 Description of heat treatment process for FEM simulation

The solution heat treatment and water quenching process of A357 alloy large complicated thin-wall workpiece are given in Fig. 3. This is a simulation of the heat treatment process, not a real experiment. The FEM simulation of quenching process in A357 alloy large complicated thin-wall work piece includes four thermal stages: heating to 540 °C, heating preservation, quenching transferring and quenching. As shown in Fig. 3, the large complicated thin-wall workpiece was heated to 540 °C in a heating time of 3 h. Then, it was maintained at 540 °C for 10 h. After 15 s air quenching transfer time, it was immersed in water at a temperature of 60 °C until it was cooled down to a uniform temperature. Three quenchants were adopted in this work (shown in Table 1).

Fig. 3 Schematic curve of heat treatment for A357 alloy large complicated thin-wall workpiece for FEM simulation

4 Result and discussion

4.1 Heat transfer coefficient calculation results

The cooling curves and the cooling rate curves of water, machine oil and 5%-UCON A were obtained from experiments, as shown in Fig. 4. It is seen that the quenching rate largely depends on the quenchants and on their temperatures. The quenching rate decreases with increasing the water temperature. The quenching rate decreases with increasing the temperature of 5%-UCON A. But the quenching rate changes very little for different temperatures of machine oil. As shown in Fig. 4(a), for the high water temperature (80 °C), cooling rate curve shows a very different trend compared with the three lower temperatures (25, 45 and 60 °C). As shown in Figs. 4(a) and (c), the tendency of cooling rate curve for water and 5%-UCON-A are the same. For water and 5%-UCON A, it can be seen that the maximum cooling velocity and temperature of probe inner point corresponding to the maximum quenching rate both decrease with increasing quenchant temperature. While for machine oil, it is found that the maximum cooling velocity and temperature of probe inner point corresponding to the maximum quenching rate both change insignificantly as the machine oil temperature changes.

Fig. 4 Cooling curves and cooling rate curves for different quenchants

A357 aluminum alloy should be quenched from the solution-treating temperature as rapidly as possible. It will minimize the precipitation phase in A357 alloy during cooling and the supersaturated solid solution phase will be retained. But at the same time, large distortion and large residual stress of A357 alloy parts will occur owing to fast quenching rate. Cooling rates during quenching are determined by heat transfer coefficients. In order to calculate and analyze the residual stress of workpieces during quenching operation, an accurate model for heat transfer coefficient should be found. The cooling curves and cooling rate curves for different quenchants (water, machine oil, 5%-UCON A) from experiments are the original data to calculate the heat transfer coefficients. Figure 5 shows the heat transfer coefficient values of three quenchants (water, machine oil, 5%-UCON A). As shown in Fig. 5, the heat transfer coefficient of machine oil is much smaller than the value of water or 5%-UCON A. The heat transfer coefficient is a function of the quenchant temperature. After obtaining the values of heat transfer coefficient, the authors import these values into the property module of Abaqus CAE software by using subroutine. Temperature at node in the core of probe (point A in Fig. 1) was calculated by using Abaqus software. With different quenchants in different temperature conditions, comparison of temperature of point A between experimental data and FEM simulation results are shown in Fig. 6. It can be seen that the FEM simulation results are very consistent with the experimental data. Therefore, heat transfer coefficient calculated by the present work can be adopted as an accurate thermal parameter for FEM simulation of quenching process of A357 alloy workpieces.

4.2 FEM simulation results

FEM simulations of quenching process in A357 alloy large complicated thin-wall workpiece were submitted by using ABAQUS CAE software. In this part, water (temperature, 60 °C) was selected as the quenchant to describe and to investigate the quenching process of A357 alloy thin-wall workpiece. The heat transfer coefficient of water at 60 °C is shown in Fig. 5(a). The heat treatment history of A357 alloy thin-wall workpiece used in FEM simulations is shown in Fig. 3.

Fig. 5 Heat transfer coefficient of quenchants

4.2.1 Temperature field results

Figure 7 shows temperature fields of A357 alloy large complicated thin-wall part during heat treatment process. Figures 7(a)-(c) show the temperature fields of thin-wall workpiece during heating process. Figure 7(d) shows temperature fields of thin-wall workpiece after 15 s quenching transfer time. Figures 7(e) and (f) show temperature fields of the workpiece during quenching process. As shown in Fig. 7(b), the temperature of work piece along axial direction displays gradient distribution and the temperature of workpiece from top to bottom shows a gradually descend trend. After 15 s of quenching transfer time, the temperature of workpiece is reduced a little. The maximum and minimum temperatures in the workpiece are 536.5 and 532.3 °C, respectively (Fig. 7(d)), indicating that 15 s of quenching transfer time is acceptable for this workpiece quenching. As can be shown in Fig. 7(e), at the beginning of quenching, the temperature difference of large complicated thin-wall workpiece is very large. As can be seen in Fig. 7(f), after 240 s of quenching time, the temperature difference of large complicated thin-wall workpiece is very small and at this time, the quenching process is considered  finished state. From Part 4.1, an accurate solution for heat transfer coefficient of water at 60 °C is achieved, which can ensure the accuracy of FEM results of temperature field of A357 alloy large complicated thin-wall workpiece during quenching operation.

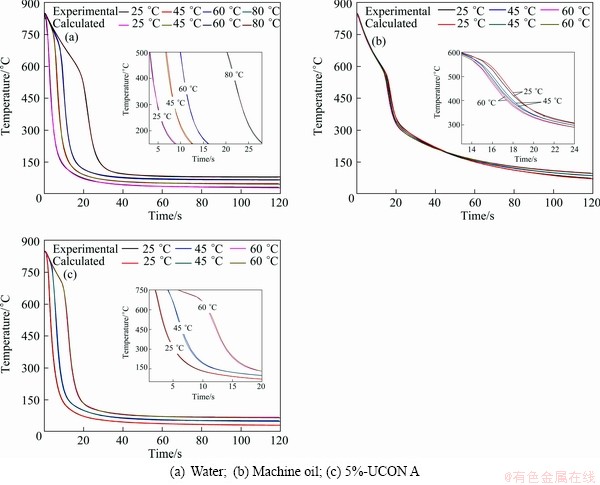
Fig. 6 Comparison between experimental data and FEM simulation results

Fig. 7 Temperature fields of A357 aluminum alloy large complicated thin-wall part during heat treatment process

Fig. 8 Residual stresses of A357 alloy large complicated thin-wall part after quenching

Fig. 9 Maximum residual stresses of six component stresses and three orthogonal principal stresses of A357 alloy large complicated thin-wall workpiece after quenching

4.2.2 Stress field results

Figure 8 shows residual stresses of A357 alloy large complicated thin-wall workpiece after quenching. The six given components of residual stress include σ_x, σ_y, σ_z, τ_xy, τ_xz and τ_yz.

As shown in Fig. 8 and Fig. 9(a), the values of normal stresses (σ_x, σ_y and σ_z) are higher than the values of shear stresses (τ_xy, τ_xz and τ_yz). For the maximum tensile residual normal stress, the value of normal stress σ_x is 170.7 MPa, which is higher than the other normal stresses σ_y and σ_z. The value of normal stress σ_z is 125.5 MPa, and it is the smallest value compared with the normal stresses σ_x and σ_y. While for the maximum compressive residual normal stress, the value of normal stress σ_z is -130.3 MPa, which is lower than the other normal stresses σ_x and σ_y. The value of normal stress σ_x is -155.3 MPa, and it is the largest value compared with the normal stresses σ_y and σ_z. For the maximum tensile residual shear stress, the value of shear stress τ_yz is 51.5 MPa, which is higher than the other shear stresses τ_xy and τ_xz. The value of shear stress τ_xz is 31.1 MPa, and it is the smallest value compared with the shear stresses τ_xy and τ_yz. While for the maximum compressive residual shear stress, the value of shear stress τ_xy is -70.4 MPa, which is higher than the other shear stresses τ_yz and τ_xz. The value of shear stress τ_xz is 41.8 MPa, and it is smaller compared with the shear stresses τ_xy and τ_yz. As shown in Fig. 9(b), for the maximum tensile residual stress, the first principal stress is 191.7 MPa, which is higher than the other principal stress. The third principal stress is 48.3 MPa, and it is smaller compared with the first and second principal stress. While for the maximum compressive residual stress, the value of first principal stress is -33.3 MPa, which is lower than the other principal stress. The third principal stress is -172.3 MPa, and it is larger compared with the first and second principal stress. As shown in Fig. 9(a), the maximum values of shear stresses (τ_xy, τ_xz and τ_yz) are much smaller than the maximum values of normal stresses (σ_x, σ_y and σ_z), So, the maximum values of normal stresses are researched.

4.3 Influence of quenchants on quenching residual stress and distortion

Water, machine oil and 5%-UCON A were selected as the quenchants to investigate the quenching residual stress and distortion of thin-wall workpieces. Figure 10 shows the maximum tensile and compressive residual normal stresses of quenched A357 alloy large complicated thin-wall workpieces along x-, y-, and z-direction with different quenchants. As can be seen from Figs. 10(a) and (b), for the quenchants of water and 5%-UCON A, the maximum tensile and compressive residual normal stresses of thin-wall workpieces along x- and y-direction decrease with increasing the quenchant temperature; for the quenchant of water, at lower water temperatures (≤60 °C), the maximum residual stresses decrease slightly with increasing the water temperature, but when the temperature is above 60 °C, the maximum residual stresses decrease obviously with increasing the water temperature. As can be seen from Fig. 10(c), for the quenchants of water and 5%-UCON A, the change of the maximum tensile residual normal stress of thin-wall workpieces along z-direction is not obvious with change of the temperature, but the maximum compressive residual normal stresses decrease with increasing the quenchant temperature. As can be seen from Fig. 10, with the quenchant of machine oil, the values of maximum residual normal stresses of thin-wall workpieces along x- and y-direction are smaller than the values of other two quenchants (water and 5%-UCON A). And the value of maximum compressive residual normal stress along z-direction is also smaller than the values of other two quenchants. But the maximum tensile residual normal stress is almost the same among these three quenchants.

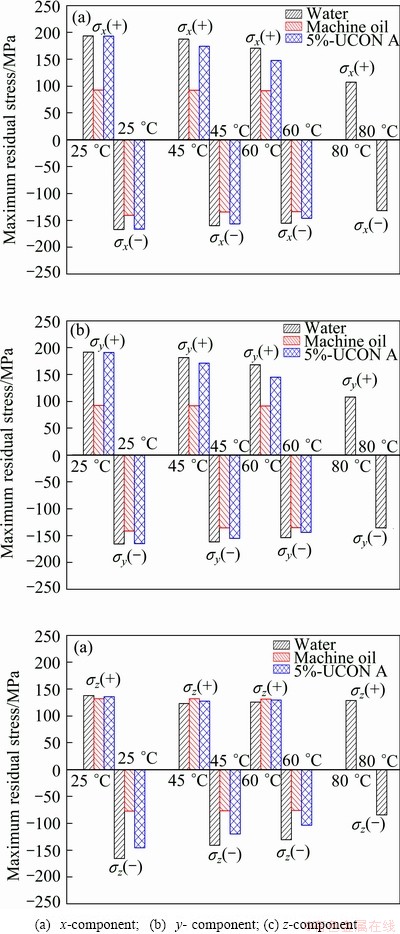
Fig. 10 Maximum residual stress of quenched A357 alloy large complicated thin-wall workpiece

Figure 11 shows the maximum distortion of quenched A357 alloy large complicated thin-wall workpieces along x-, y-, and z-direction with different quenchants under different temperature conditions. In Fig. 11, d₁, d₂, and d₃ denote x-, y- and z-component quenching distortion of thin-wall part, respectively. As can be seen from Fig. 11, the maximum distortions of quenched thin-wall workpieces along x-, y-, and z-direction increase with increasing the quenchant temperature. Based on the theory of expanding when heated and contracting when cooled, the heating expansion value of workpiece is uniform due to the same heating process, but the shrinkage of workpieces is different due to different cooling capacities. The shrinkage value of thin-wall workpieces during quenching operation decreases with increasing the quenchant temperature.

Fig. 11 Maximum distortion of quenched A357 alloy large complicated thin-wall workpiece

As shown in Fig. 10, compared with the water and 5%-UCON A, the machine oil selected for quenching aluminum can decrease the residual stress and distortion of quenched A357 alloy large complicated thin-wall workpiece. But the quenching rate of machine oil is much smaller than that of the value of 5%-UCON A or water (shown in Fig. 4). The quenching rates of 5%-UCON A and water are usually adopted in quenching aluminum alloys, but machine oil is not selected for quenching these alloys due to its lower quenching rate [26]. The quenching rates of these two quenchants (water and 5%-UCON A) in a certain temperature range are large enough not only to retain solute atoms in solution, but also to maintain a certain minimum number of vacant lattice sites to assist in promoting the low-temperature diffusion required for zone formation [26]. As can be seen from Fig. 10 and Fig. 11, with the quenchant of 5%-UCON A, the maximum residual normal stress and distortion of quenched A357 alloy large complicated thin-wall workpiece are smaller than the values with the quenchant of water.

5 Conclusions

1) The quenching rate largely depends on the quenchants and on their temperatures. For quenchants of water and 5%-UCON A, the quenching rate decreases with increasing the quenchant temperature. But the quenching rate changes very little by varying the temperature of machine oil.

2) Prediction of temperature fields of A357 alloy large complicated thin-wall workpieces after quenching by FEM simulation is credible because of accurate calculation for heat transfer coefficient of different quenchants under different temperature conditions.

3) The maximum tensile and compressive residual stress of quenched large complicated thin-wall workpiece decrease with increasing the water temperature. While for the high water temperature (80 °C), the maximum tensile and compressive residual stress are much smaller than the values in the other temperatures (25, 45 and 60 C°).

4) Machine oil is not selected for quenching A357 alloys due to its lower quenching rate. With the quenchant of 5%-UCON A, the maximum residual normal stress and distortion of quenched A357 alloy large complicated thin-wall workpiece are smaller than the values with the quenchant of water.

References

[1] KUMAR G, HEGDE S, PRABHU K N. Heat transfer and solidification behavior of modified A357 alloy [J]. J Mater Process Technol, 2007, 182 (1-3): 152-156.

[2] ES-SAID O S, LEE D, PROST W D, GAMBERINI A, MESSIERI S. Alternative heat treatments for A357-T6 aluminum alloy [J]. Eng Fail Anal, 2002, 9(1): 99-107.

[3] ALEXOPOULOS N D, PANTELAKIS S G. Quality evaluation of A357 cast aluminum alloy specimens subjected to different artificial aging treatment [J]. Mater Des, 2004, 25(5): 419-430.

[4] Callister W D. Materials science and engineering: An introduction [M]. USA: Wiley, 1994: 783-786.

[5] Prantil V C,Callabresi M L,Lathrop J F,Ramaswamy G S,Lusk M T. Simulating distortion and residual stresses in carburized thin strips [J]. J Eng Mat Tech, 2003, 125: 116-124.

[6] Ruud C O. Residual stresses and their measurement, quenching and distortion control [C]//Proc of the First International Conference on Quenching and Control of Distortion. Chicago, Illinois, USA, 1992: 193-198.

[7] Eckersley J S, Meister T J. Intelligent design takes advantage of residual stresses [C]//Proc of the 3rd International Conference on Practical Applications of Residual Stress Technology. Indianapolis, Indiana, USA, 1991: 175-181.

[8] Thakkar R, Shah R, Vanark V. Effects of hole making processes and surface conditioning on fatigue behavior of 6061-T6 aluminum [C]//SAE Technical Paper 2000-01-0783, Proc of SAE 2000 World Congress. Detroit, MI, USA, 2000.

[9] Prime M B, Newborn M A, Balog J A. Quenching and cold-work residual stresses in aluminium hand forgings: Contour method measurement and FEM prediction [J]. Mater Sci Forum, 2003, 426-432: 435-440.

[10] Robinson J S, Hossain S, Truman C E, Paradowska A M, Hughes D J, Wimpory R C. Residual stress in 7449 aluminium alloy forgings [J]. Mater Sci Eng A, 2010, 527: 2603-2612.

[11] Muammer K, John C, Taylan A. Prediction of residual stresses in quenched aluminum blocks and their reduction through cold working processes [J]. J Mater Process Tech, 2006, 174: 342-354.

[12] Tanner D A, Robinson J S. Residual stress prediction and determination in 7010 aluminum alloy forgings [J]. Exp Mech, 2000, 40(1): 75-82.

[13] Kirchlechner C, Martinschitz K J, Daniel R, Mitterer C, Donges J, Rothkirch A, Klaus M, Genzel C, Keckes J. X-ray diffraction analysis of three-dimensional residual stress fields reveals origins of thermal fatigue in uncoated and coated steel [J]. Scripta Mater, 2010, 62(10): 774-777.

[14] Ruud C O. Residual stresses and their measurement, quenching and distortion control [C]//Proc of the First International Conference on Quenching and Control of Distortion. Chicago, Illinois, USA, 1992: 193-198.

[15] Tjhung T, Li K. Measurement of in-plane residual stresses varying with depth by the interferometric strain/slope rosette and incremental hole-drilling [J]. J Eng Mat Tech, 2003, 125: 153-162.

[16] El-Baradie Z M, El-Sayed M. Effect of double thermo mechanical treatments on the properties of 7075 Al alloy [J]. J Mater Process Tech, 1996, 62(1-3): 76-80.

[17] Todinov M T. Influence of some parameters on the residual stresses from quenching [J]. Modelling Simul Mater Sci Eng, 1999, 7(1): 25-41.

[18] Li H P, Zhao G Q, Niu S T, Huang C Z. FEM simulation of quenching process and experimental verification of simulation results [J]. Mater Sci Eng A, 2007, 452-453: 705-714.

[19] LI H P, ZHAO G Q, HUANG C Z, NIU S T. Technological parameters evaluation of gas quenching based on the finite element method [J]. Comp Mater Sci, 2007, 40(2): 282-291.

[20] Beck J V, Blackwell B. Inverse heat conduction: III-posed problems [M]. New York: John Wiley & Sons, Inc, 1985: 218-242.

[21] Ozisik M N. Inverse heat transfer: Fundamentals and application [M]. UK: Taylor & Francis Group, 2000: 214-225.

[22] YANG X W, Zhu J C, Lai ZH, Kong Y R, Zhao R D, He D. Application of artificial neural network to predict flow stress of as quenched A357 alloy [J]. Mater Sci Tech, 2012, 28(2): 151-155.

[23] YANG X W, Lai Z H, Zhu J C, Liu Y, He D. Hot compressive deformation behavior of the as-quenched A357 aluminum alloy [J]. Mater Sci Eng B, 2012, doi: 10.1016/j.mseb.2012.02.020.

[24] LIN Gang, LIN Hui-guo, ZHAO Yu-tao. Aluminum alloy application manual [M]. Beijing: China Machine Press, 2006: 542. (in Chinese)

[25] PAN Fu-sheng, ZHANG Ding-fei, et al. Aluminum alloy and its application [M]. Beijing: Chemical Industry Press, 2006: 266-267. (in Chinese)

[26] Charlie R. ASM metals handbook: Heat treating [M]. Materials Park, OH: ASM International, 1991: 1892-1912.

A357铝合金大型复杂薄壁构件的淬火温度场、残余应力及变形的有限元分析

杨夏炜^1,2, 朱景川^1,2, 来忠红^1,2, 刘 勇^1,2, 何 东^1,2, 农智升^1,2

1. 哈尔滨工业大学 金属精密热加工国家级重点实验室，哈尔滨 150001；

2. 哈尔滨工业大学 材料科学与工程学院，哈尔滨 150001

摘  要：基于ABAQUS软件，采用有限元模拟计算的方法对A357铝合金大型复杂薄壁构件的淬火过程进行研究。通过采用传统的反传热方法，对不同淬火介质在不同温度下的换热系数进行精确求解。精确的换热系数确保对A357铝合金大型复杂薄壁构件淬火过程中温度场预测的准确性。采用3种淬火介质 (水、机油，5%-UCON淬火试剂A)。通过综合考虑淬火介质及温度因素，对薄壁构件的残余应力及变形的分布和大小进行有限元预测，得到构件淬火结束后的最大残余应力及变形。

关键词：A357铝合金；复杂薄壁构件；有限元模拟；残余应力；变形

(Edited by Hua YANG)

Corresponding author: Jing-chuan ZHU; Tel/Fax: +86-451-86413792; E-mail: fgms@hit.edu.cn

DOI: 10.1016/S1003-6326(13)62657-6