J. Cent. South Univ. (2016) 23: 3332-3345

DOI: 10.1007/s11771-016-3399-z

Analysis of chamber effect on intermittent pulsation

Tang Chan(唐婵)^{1, 2}, Zhang Jing-zhou(张靖周)^{1, 3}, Tan Xiao-ming(谭晓茗)¹, WANG Chun-hua(王春华)¹

1. College of Energy and Power Engineering, Jiangsu Province Key Laboratory of Aerospace Power System,

Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;

2. College of Energy and Power Engineering, Nanjing Institute of Technology, Nanjing 211167, China;

3. Collaborative Innovation Center of Advanced Aero-Engine, Beijing 100191, China

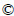Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: A numerical study was conducted to seek an optimized dimension of jet chamber in the pulsating impinging flow. The flow and heat transfer effect of the pulsation flow through a jet chamber was investigated. The numerical results indicate that heat transfer effective enhances near the stagnation region for the intermittent pulsed flow with jet chamber compared to that without jet chamber. Simulations of the flow through a jet chamber show that the heat transfer rate on the impingement surface is highly dependent on the velocity at the position which is really close to target surface. Examination of the velocity field suggests that the velocity exists a maximum value as the axis distance increases. In addition, the velocity at the jet hole is enlarged by the jet chamber due to the entrainment effect, and the velocity is amplified even greater as the size of the jet chamber becomes bigger. Nevertheless, the velocity declines quickly while the flow axis distance is more than a certain range, leading to poor heat transfer. Thus, intermittent pulsed flow with jet chamber is suggested as a method of improving heat transfer by employing larger dimensions of jet chamber for appropriate jet-to-surface spacing.

Key words: pulsed impinging jet; intermittent pulsation; jet chamber; Nusselt number

1 Introduction

Research activities about jet impinging technique cover a wide range of various cooling, heating and drying applications in many industrial fields, from electronic component and gas turbine blade cooling, de- icing for aircraft wing, to thermal drying of materials and foodstuffs and printing processes [1-2]. Impinging jets can achieve high local heat transfer rates in the stagnation region because the jet flow establishes very thin hydrodynamic and thermal boundary layers. By imposing a pulsating flow to a steady jet, the heat transfer can be enhanced. The effect of frequency and amplitude of the pulsated jet has been examined for different Reynolds numbers and nozzle-to-plate distances; high frequency pulsation jet at small nozzle-to-plate distances has yielded increased heat transfer coefficients at the stagnation point [3]. A special mass flow rate control system has been used to provide various shapes of unsteadiness and various frequencies of jet flow in the experimental investigation. Compared to sinusoidal and triangular signals, the rectangular signal jet has been found a good performance on the heat transfer effective [4-6]. In recent years, many studies have appeared in the literature aimed at single jet [7-11]. The influence of single pulse jet has been studied by LIEWKONGSATAPORN et al [12]; large velocity amplitude has helped to enhance heat transfer by high jet velocity during the positive cycle and strong recirculating flows during the negative cycle. It is noteworthy that most of studies have concentrated on prediction of enhanced impingement heat transfer from the target surface through multiple pulsing impinging jet. As pointed out by JANETZKE et al [13-14], the cooling effectiveness of periodically pulsating impinging air jets depending on the combination of the relevant excitation parameters, Strouhal number and pulsation magnitude, has been investigated experimentally. The pulsations with phase angle difference, which can eliminate the formation of a static stagnation point and enhance the local Nusselt number along the impingement wall between adjacent jets, have significantly improved convective heat transfer rate [15-16]. MOHAMMADPOUR et al [17-18] observed impingement flow on the concave surface and reported that higher heat transfer can be obtained by the combinations of intermittent-steady jets rather than the sinusoidal-steady ones. The mechanisms of convective heat transfer in periodic pulsed flow have been widely examined, but only few knowledge exists about the chamber effect when the pulsating flow through a cavity before the jet impinging on the surface from the hole.

Further studies are therefore needed to examine the effect of the intermittent pulsation on heat transfer in impinging flow through a jet chamber. In the current study, the characteristic of a two-dimensional turbulent slot air impinging jet subjected to intermittent pulsation is investigated numerically. The effect of dimensions of the jet chamber on the flow characteristics and heat transfer is discussed.

2 Method of analysis

A two-dimensional axisymmetric impinging jet configuration as shown in Fig. 1 was modeled. The air jet was injected from the slot nozzle through a jet chamber (Fig. 1(b)) impinged on the target surface. Compared to the one without a jet chamber (Fig.1(a)), an constant heat flux surface with no-slip condition was considered for the impingement surface. The confinement wall was specified to be adiabatic. The jet-to-surface spacing, slot jet width, the height of the jet chamber, the width of the jet chamber and the half width of the impingement wall were defined as H, w, H_c, L_c and L, respectively.

Grid-independence study was carried out to make sure the selected mesh used for this geometry that gives a mesh independent solution. Typically, a mesh configuration with 160×300 control volumes along the axial and radial directions was provided the needed accuracy in solving the present problem to compute the half physical domain as shown in Fig. 2. The elements were grown proportionately packing a large number of nodes closer to the bottom boundary in order to capture the boundary layer development. Considering the importance of spying the local gradient around the jet hole through which the air jet is from the jet chamber to impact chamber, a structured mesh with elements closely packed near the jet hole was used.

Numerical simulation of the flow and thermal fields in the computational domain requires solving the continuity Eq. (1), momentum Eq. (2) and energy Eq. (3) conservation equations which could be expressed as follows:

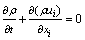                             (1)

Fig. 1 Physical model and grid division of pulsed slot impinging flow:

Fig. 2 Grid division of physical domain:

(2)

  (3)

where is the Reynolds stress tensor; is the turbulence heat flux vector; t is the flow time; p is the mean pressure; T_f is the mean temperature; T_f' is the fluctuating temperature; u_i and u_j are the mean velocities; u_i' and u_j' are the fluctuating velocities; x_i and x_j are the coordinate directions; ρ, μ, k and c_p are the fluid density, dynamic viscosity, thermal conductivity and specific heat capacity, respectively.

Because the speed of the fluid was low, the fluid could be assumed to be incompressible and Newtonian fluid with temperature-dependent fluid properties. The intermittent pulsation with a uniform velocity profile (Fig. 3) was applied at the inlet of the impinging jet as described below, where T was the periodic time:

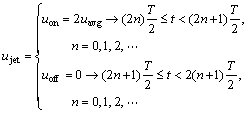     (4)

Due to geometric and flow symmetry, only the flow field within the half domain was solved. All calculations were carried out for air at atmospheric pressure. The initial conditions (t=0) throughout the computational domain could be described as: u=v=0, p=p_∞, T_f=T_∞. The flow and thermal fields were computed with the finite volume computational fluid dynamics (CFD) code FLUENT. It has been reported that in comparison with other turbulence models, the renormalization group (RNG) k-ε model is numerically robust and fast, and has been proven to be effective in predicting the complexities of flow impingement [19-22]. Thus, in the current study, RNG k-ε model was used to model the turbulent behavior of the flow in the pulsating impinging jet, and the near-wall treatment was employed the enhanced wall treatment. The quality of a computational solution was strongly linked to the quality of the grid mesh. The first cell was located at a distance y⁺=yU*/v≈1 from the wall to resolve the velocity field and turbulence quantities in the viscosity-affected near-wall region, where U* is the friction velocity obtained for the flow .

Fig. 3 Square waveform of velocity profiles at inlet jets

Mass, momentum and energy conservation equations were discretized by the control volume method. The SIMPLEC algorithm was employed for pressure- velocity coupling, and a second-order upwind discretization method has been employed to consider the stability of solution convergence. In this numerical study, convergence was obtained when the normalized residuals were less than 10^-8 for the steady case parameters and less than 10^-6 for all the transient variables. The time-step independence was also checked for each case and the time-step has been used as 10^-4 s in the unsteady simulation. The simulations were run as long as the oscillation of flow and temperature fields become stable, namely, repeating results over one cycle are as the previous cycles.

Reynolds and Nusselt numbers are defined based on the hydraulic diameter of the nozzle, which is equal to w as shown below:

Re=ρu_avgw/μ                               (5)

                           (6)

where q_w and k are the heat flux and the thermal conductivity of fluid, respectively.

In the pulsating flow case, the Nusselt number depends on time and position; therefore for calculation of the local Nusselt number, Eq. (7) is used to average the Nusselt number values.

                    (7)

where △t is the periodic cycle numbers multiply by the time of each period; dt is the time step.

This numerical method has been validated by comparison with experimental results [9], where the Reynolds number of jet flow ranged from 6000 to 14000. One of typical case for H/w=6 at Re=6000, w=13 mm, pulsation frequency f=9 Hz, Strouhal number Sr=fw/u_avg= 0.017, fixed surface temperature T_w =333 K and ambient fluid temperature T_f =298 K is shown in Fig. 4. It is clear that the numerical predictions of local Nusselt number show good agreement with experimental data for both steady and unsteady situations.

As expected, the half of physical model (Fig. 1) was set as the computational domain for the axisymmetric model. The performance of pulsed flow without a jet chamber was compared with that of steady flow. A description of the pulsating flow without jet chamber was included as a benchmark for the oscillatory flow throughout a jet chamber of different sizes. To explain the flow and heat transfer mechanisms, the width of the nozzle slot w=15 mm, the impact chamber configuration H/w =6 and L/w=20 were considered. The symmetry and fully developed outflow boundary conditions were taken at symmetry and outlet planes. The jet flow inlet was provided as the velocity inlet using the UDF profile as explained in Fig. 3 with jet mean Reynolds number Re= 7500, pulsation frequency f=10 Hz, Strouhal number Sr=fw/u_avg=0.015. The temperature at the inlet jet and the heat flux of the impinging surface were considered constant, T_jet=300 K and q_w =420 W/m², respectively.

Fig. 4 Comparison of time-averaged local Nusselt number along impingement wall between numerical model and experimental results [9]

3 Results and discussion

3.1 Pulsed flow without jet chamber

In order to compare the heat transfer rates on the impingement wall, the injected mass flow rate was kept as the same for steady and pulsed jet. Figure 5(a) shows the numerically predicted velocity profile distribution in a steady impinging(f=0) jet. Figures 5(b)-(e) indicate the variations of the velocity magnitude and streamtraces of a pulsed impinging jet at various times during one representative cycle. It can be seen from Fig. 5 that a vortex near the target surface of the steady impinging jet is weak; while in the pulsed impinging jet, two stronger vortexes can be found near the impinging surface from the beginning of the cycle (Fig. 5(b)); the two vortexes increase with fluid flow injection (Fig. 5(c)) and are present even when the pulsation is in the off mode (closed state Figs. 5(d) and (e)). The relatively strong vortex is believed to increase flow entrainment and mixing, and contribute to the predicted heat transfer enhancement in the pulsed impinging jet. For the pulsed jet, flow pulsation generally improves the heat transfer rate, which can be seen in Fig. 6. The mechanism leading to higher heat transfer rates is considered to be the periodic disruption of the boundary layer.

3.2 Pulsed flow through jet chamber

Based on Fig. 1, pulsed jet without jet chamber could be considered a special case with both the height of the jet chamber H_c and the width of the jet chamber L_c equal to zero(H_c/w=L_c/w=0 ). In this section, the effect of dimensions of the jet chamber on the flow characteristics and heat transfer is analyzed in detail. There were four cases with jet chamber discussed, such as H_c/w=L_c/w=2, H_c/w=L_c/w=3, H_c/w=2L_c/w=4 and H_c/w=2L_c/w=6, which belong to two types of cases H_c/L_c=1 and H_c/L_c=2, respectively.

Fig. 5 Velocity magnitude and streamtraces plots in impinging jet for f =0 Hz steady jet (a) and f=10 Hz intermittent pulsed jet in one representative cycle at t/T=0.25 (b), t/T=0.5 (c), t/T=0.75 (d) and t/T=1 (e) (Velocity unit: m/s)

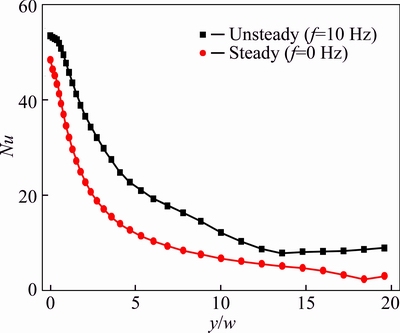
Fig. 6 Local Nusselt number profiles for a steady impinging jet (f=0) compared to time-averaged distribution local Nusselt number of intermittent pulsed jet (f=10 Hz)

To explore the behavior of the intermittent pulsed flow through a jet chamber, the velocity field plots and partial enlarged velocity drawings at the jet hole from the jet chamber to impact chamber are shown in Fig. 7 and Fig. 8 for the case H_c/L_c=1 and Fig. 9 and Fig. 10 for the case H_c/L_c=2. Figures 7-10 illustrate that vortexes can be found near the impinging surface and in the jet chamber, the vortexes increase in the jet chamber and present near the confinement wall as the pulsation is in the off mode. That is because there are entrainment velocity from the impact chamber to jet chamber near the jet hole when u_jet=u_off. Owing to the effect of chamber, the differential pressure and velocity magnitude at the jet hole are enlarged by the jet chamber, leading to a larger velocity impinging from the jet hole compared to the nozzle exit at the same Reynolds number. Heat transfer rates are generally dependent on the jet velocity. With the same width of the jet chamber L_c, the larger the height H_c the weaker entrainment near the jet hole, as indicated in Fig. 7, Fig. 9 and Fig. 8, Fig. 10. Meanwhile, it can be found larger velocity magnitude and stronger turbulence near the jet hole of the case H_c/L_c=2 compared to the case H_c/L_c=1.

The jet velocity at any location is normalized with the mean velocity at the nozzle exit and labeled as U=u/u_avg. The chamber entrainment effect becomes apparent in Figs. 12-15, which indicate the local jet velocity at selected positions of typical time in a representative period for the case H_c/w=L_c/w=2, H_c/w= L_c/w=3 and H_c/w=2L_c/w=4, H_c/w=2L_c/w=6, compared favorably with the case H_c/w=L_c/w=0 illustrated in Fig. 11. The selected location inlet and x/w=0 refer to the nozzle exit and the jet hole, which both of them overlap in the case H_c/w=L_c/w=0. It has been observed that the velocity profile becomes significant curve, which shows that the closer the distance of the hole center, the greater the velocity, as the axis distance increases. To compare the case without jet chamber, it has been observed that jet velocity is enhanced at the jet hole (x/w=0) when the pulsation is in the mode and obviously much enlarged at the time t/T=0.5 for the cases with jet chamber (Figs. 12(a) and (b), Figs. 13(a) and (b), Figs. 14(a) and (b), Figs. 15(a) and (b)). Another noticeable feature is that the increasing degree of the jet velocity becomes larger, as the dimensions of the jet chamber increase. For example, the velocity of the position near the jet hole (x/w=1, x/w=2, x/w=3, x/w=4) is magnified much more in the case H_c/L_c=2 than in the case H_c/L_c=1. By the way, there is more incremental degree of the velocity in the case H_c/w=L_c/w=3 than in the case H_c/w=L_c/w=2; the similar conclusion as in the case H_c/w=2L_c/w=6 than in the case H_c/w=2L_c/w=4. However, the chamber effect leading to velocity amplification does not so good as the distance from the jet hole increases. It can be seen from the position (x/w=5). The velocity reduction becomes larger in the case H_c/L_c=2 than in the case H_c/L_c=1. The highest mean velocity of position x/w=1 and the lowest mean velocity of position x/w=5 are both in the case H_c/w=2L_c/w=6. According to Figs. 12(c) and (d), Figs. 13(c) and (d) and Figs. 14(c) and (d), Figs. 15(c) and (d), despite the velocity from the nozzle exit equals zero, there is also speed oscillation at the jet hole and in the impact chamber at the end of the cycle. Therefore,the air flow through a chamber could be accelerated; while in the mode of u_jet=u_on, the bigger the sizes of the chamber are, the larger the velocity becomes; but as the distance from the jet hole increases, the enlargement effect cuts down and the mean velocity becomes smaller in the case with bigger chamber measurements. While in the mode of u_jet=u_off, there are nearly no difference of the velocity profile between the cases; but as the distance from the jet hole increases, the mean velocity becomes larger, and the largest velocity is in the position of x/w=5.

Fig. 7 Velocity magnitude, velocity streamtraces plots and partial enlargement for f=10 Hz intermittent pulsed flow through jet chamber with H_c/w=L_c/w=2(H_c/L_c=1) in one representative cycle:(Velocity unit: m/s)

Fig. 8 Velocity magnitude, velocity streamtraces plots and partial enlargement for f=10 Hz intermittent pulsed flow through jet chamber with H_c/w=L_c/w=3(H_c/L_c=1) in one representative cycle:(velocity unit: m/s)

The square wave impinging flow with jet chamber because of creating much stronger vortexes near the jet hole resulting in bigger jet velocity is superior to that without jet chamber. Figure 16 presents the predicted time-averaged local Nusselt number distributions on the target surface at various size of jet chamber for intermittent pulsed impinging jet, compared with the case without jet chamber (H_c/w=L_c/w=0). It is clear that the time-averaged local Nusselt number near the stagnation line(y/w=0) in the cases with jet chamber is larger than that for the corresponding case without jet chamber. And not clear enhancement of heat transfer can be found in the impinging wall as the distance from the stagnation point is far. However, a little higher enhancement is obtained from the cases H_c/L_c=1 compared to H_c/L_c=2 ones at the stagnation region. The trend is that the higher velocity magnitudes enhance the heat transfer.

Fig. 9 Velocity magnitude, velocity streamtraces plots and partial enlargement for f=10 Hz intermittent pulsed flow through jet chamber with H_c/w=2L_c/w=4(H_c/L_c=2) in one representative cycle:(Velocity unit: m/s)

Fig. 10 Velocity magnitude, velocity streamtraces plots and partial enlargement for f=10 Hz intermittent pulsed flow through jet chamber with H_c/w=2L_c/w=6(H_c/L_c=2) in one representative cycle:(Velocity unit: m/s)

It can be explained from Fig. 17 why the bigger velocity at the jet hole but poor heat transfer rate near the stagnation region is obtained from the case H_c/L_c=2. Normalized mean velocity profiles of a cycle in steady (f=0 Hz) and pulsating jet (f=10 Hz) for different sizes of jet chamber at different axial distances ((a) x/w=-1, (b) x/w=-1/6 (negative value for x means in the jet chamber (Fig. 1)), (c) x/w=0, (d) x/w=1, (e) x/w=2, (f) x/w=3, (g) x/w=4, (h) x/w=5) are shown in Fig. 17. Whereas H_c/w=L_c/w=0 and f=0 Hz are considered the pulsed and steady flow without jet chamber. The selected location x/w=-1 and x/w=-1/6 refer to representative surface in the jet chamber. It can be found that the velocity magnitude in the jet chamber of the cases H_c/L_c=2 (H_c/w=6, L_c/w=3 and H_c/w=4, L_c/w=2) is smaller than the ones H_c/L_c=1 (H_c/w=3, L_c/w=3 and H_c/w=2, L_c/w=2) shown in Fig. 17(a). Further, there is a trend for the velocity magnitude of the cases H_c/L_c=2 exceeds the ones H_c/L_c=1 at the x/w=-1/6 pretty near the jet hole (Fig. 17(b)). After flowing through the jet hole (Fig. 17(c)), an obvious rise of velocity by the cases H_c/L_c=2, which leads to the velocity magnitude superiors to the ones H_c/L_c=1, especially near the stagnation region (Figs. 17(d)-(f)). The velocity begins to increase when the axis distance is less than 3, and then decreases after that. Nevertheless, this trend is not evident as the axis distance x/w increases greater than 4 (Fig. 17(g)), while it is even a bit inferior to the cases H_c/L_c=1 as described in Fig. 17(h). Consequently, the variations of the Nusselt number along the impingement surface have been carried out due to the velocity at the very close distance off the target surface. It is noticeable that the jet-to-surface spacing for the impinging model with jet chamber has so important effect on the heat transfer as a result of velocity decay. That’s why the intermittent pulsating impinging flow with jet chamber of smaller sizes indicates a little advantage at the stagnation region in heat transfer enhancement compared with that of bigger sizes. One point should also be noted that U for the case H_c/w=L_c/w=3 remains well above the values for the case H_c/w=L_c/w=2 showing better heat transfer efficiency when the axis distance x/w is less than 4, as well as both cases get quite close to each other when x/w=5, resulting in close heat transfer in this numerical experiments for jet-to-surface spacing H equal to 6. Whereas the case H_c/w=2L_c/w=6 suggests no more superiority for the case H_c/w=2L_c/w=4 when the axis distance x/w is greater than 1, leading to no significant enhancement of heat transfer at the target surface in the two cases.

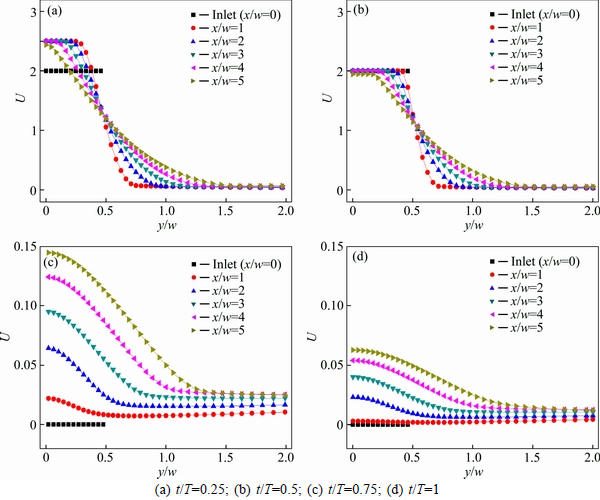
Fig. 11 Normalized velocity profiles in pulsating jet (f=10 Hz) at different axial distances for typical time in a cycle:(From case H_c/w=L_c/w=0)

Fig. 12 Normalized velocity profiles in pulsating jet (f=10 Hz) at different axial distances for typical time in a cycle:(From case H_c/w=L_c/w=2)

Fig. 13 Normalized velocity profiles in pulsating jet (f=10 Hz) at different axial distances for typical time in a cycle:(From case H_c/w=L_c/w=3)

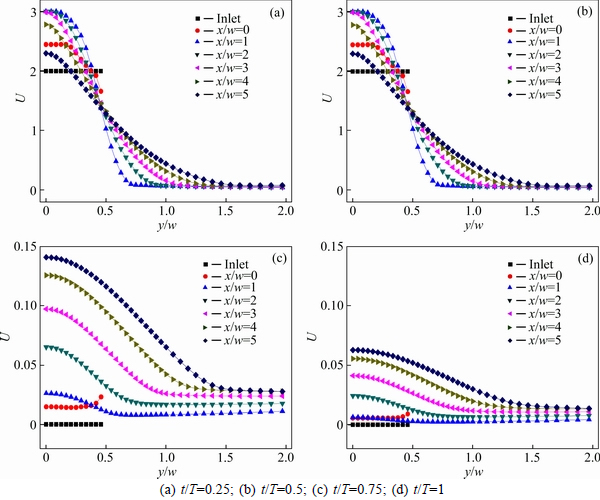
Fig. 14 Normalized velocity profiles in pulsating jet (f=10 Hz) at different axial distances for typical time in a cycle:(From case H_c/w=2L_c/w=4)

Fig. 15 Normalized velocity profiles in pulsating jet (f=10 Hz) at different axial distances for typical time in a cycle:(From case H_c/w=2L_c/w=6)

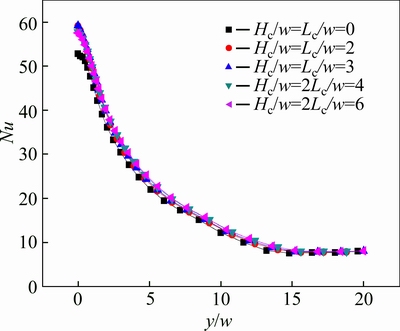
Fig. 16 Effect of dimensions of jet chamber on time-averaged local Nusselt number along impingement wall at H/w =6, f=10 Hz, Re=7500, T_jet=300 K and q_w =420 W/m²

Fig. 17 Normalized mean velocity profiles of a cycle in steady (f=0 Hz) and pulsating jet (f=10 Hz) at different axial distances:(from nozzle for different dimensions of jet chamber)

4 Conclusions

Therefore, much higher enhancement is obtained from intermittent flow compared to steady one. The stronger vortexes are believed to increase flow entrainment and mixing, and contribute to the predicted heat transfer enhancement in the pulsed impinging jet. It is obvious that entrainment effect emerged in the pulsating flow through jet chamber causes greater velocity at the jet hole. As the axis distance increases, the velocity begins to increase then decrease, and even change to the opposite trend for the cases with jet chamber. Furthermore, it is expected that the velocity which was supposed to be the influencing factor of the heat transfer is nonlinearly influenced by the distance from the jet hole in the model with jet chamber. Intermittent pulsed flow with jet chamber operating cooperatively out of appropriate dimensions is suggested as a method of improving heat transfer.

References

[1] POLAT S. Heat and mass transfer in impingement drying [J]. Drying Technology,1993,11(6): 1147-1176.

[2] Martin H. Heat and mass transfer between impinging gas jets and solid surface [J]. Advanced Heat Transfer, 1977, 13: 1-60.

[3] Hofmann H M, Movileanu D L, Kind M, Martin H. Influence of a pulsation on heat transfer and flow structure in submerged impinging jets [J]. International Journal of Heat and Mass Transfer, 2007,50(17): 3638-3648.

[4] Herwig H, Middelberg G. The physics of unsteady jet impingement and its heat transfer performance [J]. Acta Mechanica, 2008,201(1/2/3/4): 171-184.

[5] Middelberg G, Herwig H. Convective heat transfer under unsteady impinging jets: The effect of the shape of the unsteadiness [J]. Heat and Mass Transfer, 2009,45(12): 1519-1532.

[6] Zhou Jing-wei, Wang Yu-gang, Middelberg G, Herwig H. Unsteady jet impingement heat transfer on smooth and non-smooth surfaces [J]. International Communications in Heat and Mass Transfer, 2009,36(2): 103-110.

[7] Pakhomov M A, Terekhov V I. Effect of pulse frequency on heat transfer at the stagnation point of an impinging turbulent jet [J]. High Temperature, 2013,51(2): 256-261.

[8] Medina H, Benard E, Early J M. Reynolds number effects on fully developed pulsed jets impinging on flat surfaces [J]. AIAA Journal, 2013,51(10): 2305-2318.

[9] Persoons T, Balgazin K, Brown K, MURRAY D B. Scaling of convective heat transfer enhancement due to flow pulsation in an axisymmetric impinging jet [J]. Journal of Heat Transfer, 2013,135(11): 803-816.

[10] ASTARITA T, CARDONE G. Convective heat transfer on a rotating disk with a centred impinging round jet [J]. International Journal of Heat & Mass Transfer, 2008, 51(7/8): 1562-1572.

[11] WANG Bing-xing, XIE Qian, WANG Zhao-dong, WANG Guo-dong. Fluid flow characteristics of single inclined circular jet impingement for ultra-fast cooling [J]. Journal of Central South University, 2013, 20: 2960-2966.

[12] Liewkongsataporn W, Patterson T, AHRENS F. Pulsating jet impingement heat transfer enhancement [J]. Drying Technology, 2008,26(4): 433-442.

[13] Janetzke T, Nitsche W, Tage J. Experimental investigations of flow field and heat transfer characteristics due to periodically pulsating impinging air jets [J]. Heat and Mass Transfer, 2008,45(2): 193-206.

[14] Janetzke T, Nitsche W. Time resolved investigations on flow field and quasi wall shear stress of an impingement configuration with pulsating jets by means of high speed PIV and a surface hot wire array [J]. International Journal of Heat and Fluid Flow, 2009,30(5): 877-885.

[15] Xu Peng, Qiu Shu-xia, Yu Ming-zhou, QIAO Xian-wu, MUJUMDAR A S. A study on the heat and mass transfer properties of multiple pulsating impinging jets [J]. International Communications in Heat and Mass Transfer, 2012,39(3): 378-382.

[16] SHI Jian-hui, YUAN Guo, JIANG Lian-yun, ZHAO Kun, WANG Guo-dong. Numerical analysis of heat transfer intensity from twin slot vertical jet impingement on strip surface after hot rolling [J]. Journal of Central South University, 2015, 22: 2816-2824.

[17] Mohammadpour J, Rajabi-Zargarabadi M, Mujumdar A S, AHMADI H. Effect of intermittent and sinusoidal pulsed flows on impingement heat transfer from a concave surface [J]. International Journal of Thermal Sciences, 2014, 76: 118-127.

[18] Mohammadpour J, Zolfagharian M M, Mujumdar A S, ZARGARABADI M R, MOHAMMAD A. Heat transfer under composite arrangement of pulsed and steady turbulent submerged multiple jets impinging on a flat surface [J]. International Journal of Thermal Sciences, 2014, 86: 139-147.

[19] Liakos H H, Keramida E P , Founti M A , Markatos N C, Heat and mass transfer study of impinging turbulent premixed flames [J]. Heat Mass Transfer, 2002, 38(4/5): 425-432.

[20] Zhang Jing-zhou, Xie Hao, Yang Cheng-feng. Numerical study of flow and heat transfer characteristics of impingement/effusion cooling [J]. Chinese Journal of Aeronautics, 2009, 22(4): 343-348.

[21] Parham K, Esmaeilzadeh E, Atikol U, Aldabbagh L B Y. A numerical study of turbulent opposed impinging jets issuing from triangular nozzles with different geometries [J]. Heat Mass Transfer, 2010,47(4): 427-437.

[22] Sharif M A R, Mothe K K. Parametric study of turbulent slot-jet impingement heat transfer form concave cylindrical surfaces [J]. International Journal of Thermal Science, 2009, 49(2): 428-442.

(Edited by YANG Hua)

Foundation item: Project(51306088) supported by the National Natural Science Foundation of China; Project(NJ20160039) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2016-01-30; Accepted date: 2016-05-09

Corresponding author: TANG Chan, Lecturer, PhD; Tel: +86-13951911029; E-mail: jiyasi2102@163.com