FE-based coupling simulation of Ti60 alloy in isothermal upsetting process

LUO Jiao(罗 皎), LI Miao-quan(李淼泉)

School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

Received 20 March 2009; accepted 15 June 2009

Abstract: A constitutive equation was proposed to describe the effect of grain size on the deformation behavior. And a coupling simulation of deformation with heat transfer and microstructure was carried out in isothermal upsetting process of Ti60 alloy. The effects of processing parameters on the equivalent strain, the equivalent stress, the temperature rise and the grain size distribution in isothermal upsetting process of Ti60 alloy were analyzed. It is concluded that the uniformity of equivalent strain and equivalent stress increases with the increase of deformation temperature. However, the temperature rise and the grain size decreases with the increase of deformation temperature. The non-uniformity of equivalent strain, equivalent stress, temperature field and grain size increases with the increase of height reduction. And the calculated grain size using simulation is in good agreement with the experimental one.

Key words: titanium alloy; coupling simulation; constitutive equation; grain size

1 Introduction

Deformation behavior of titanium alloys is strongly sensitive to the processing parameters, and the microstructure evolution in high temperature deformation affects significantly the mechanical properties of the work piece. Therefore, more and more attention has been paid to not only the investigation of the deformation behavior in high temperature deformation of titanium alloys, but also the prediction and control of the microstructure in order to obtain excellent mechanical properties. With the development of computer technology and plastic theory, finite element method (FEM) was widely used to simulate the deformation processes and predict the microstructure change of metals or alloys. For instance, LIN[1] adopted the finite-element method and the finite-difference method to simulate the plastic upsetting process of a cylinder. WANG et al[2] developed a thermoviscoplastic finite element-based software to predict the microstructure and mechanical properties of the forged products. NA et al[3] used the 3D FE simulator combined with a microstructure model to simulate the forging process of superalloy 718 aerofoil blades. LI and LI[4] simulated the forging process of TC6 titanium alloy disc utilising a microstructural model. ZHANG et al[5] reported the effects of friction factor and sidewall thickness on metal flow and boss forming by finite element method and experiments. GAO et al[6] obtained the distribution laws of the microstructure in the typical section under different processing parameters during the blade precision forging process of the titanium alloy. Prior to the simulation, it is necessary to realize the modeling of flow stress and microstructure evolution. In the past several decades, many empirical/semi-empirical or physical models describing the deformation behavior and microstructure change of alloys had been reported[7-18]. However, those models did not reveal the interaction between the microstructure evolution and the deformation behavior. So, further investigations are needed so as to model the deformation behavior in high temperature deformation based on physical mechanism of plastic deformation.

The cylinder upsetting is often used to examine the deformation behavior and/or as a pre-deformation in metal forming. The homogeneous deformation will occur in the upsetting process without friction. However, the apparent simplicity turns into a complex deformation when friction is presented at the contact surface between die and work piece[19]. The barrels and fracture may occur at the free surface because the non-uniform stress distribution exists in the cylinder upsetting process. Therefore, the deformation behavior, including the strain and the stress distribution and the microstructure evolution, should be investigated in the upsetting process so as to optimize the processing parameters and to control mechanical properties.

In this work, a constitutive equation, which describes an interaction of the flow stress with the microstructure evolution in high temperature deformation of Ti60 alloy, has been established based on the analysis of deformation behavior. The upsetting process of Ti60 alloy has been simulated through FEM in order to study the effect of processing parameters on the equivalent strain, the equivalent stress, the temperature rise and the grain size.

2 Experimental

The nominal composition of Ti60 alloy was as follows (mass fraction): 5.6% Al, 4.8% Sn, 2.0% Zr, 1.0% Mo, 0.35% Si, 0.05% C, 0.85% Nd and balance Ti. The optical micrograph of as-received Ti60 alloy is shown in Fig.1. It was seen from Fig.1 that the starting microstructure consisted of an equiaxed primary α phase with a grain size of about 6.0 μm and a small amount of intergranular β. The β transus temperature for this alloy was determined to be 1 030 ℃ via a technique involving heat treatment followed by optical metallography.

Fig.1 Optical micrograph of as-received Ti60 alloy

Isothermal compression was conducted at a Thermecmaster-Z simulator at the deformation temperatures of 900, 930, 960, 970, 980, 990 and 1 000 ℃, the strain rates of 0.001, 0.01, 0.1, 1.0 and 10.0 s^-1, and the height reductions of 50%, 60% and 70%. The ends of cylindrical compression specimens were grooved for retention of glass lubricants in isothermal compression of Ti60 alloy. Fig.2 illustrates the selected flow stress-strain curves of Ti60 alloy at different deformation temperatures and strain rates.

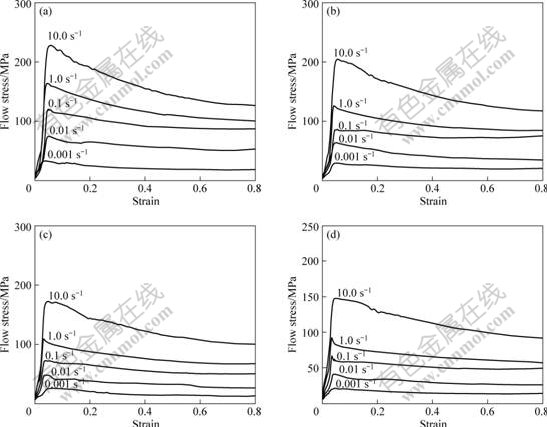
Fig.2 Selected flow stress-strain curves of Ti60 alloy at different deformation temperatures: (a) 960 ℃; (b) 970 ℃; (c) 980 ℃; (d) 990 ℃

After isothermal compression, the specimens were cooled in air to room temperature. The isothermally compressed Ti60 alloy specimens were axially sectioned and prepared using standard metallographic techniques. And four measurement points and two visual fields of one point in different deformation regions were chosen, as presented in Fig.3. The grain size was measured at an OLYMPUS PMG3 microscope with the quantitative metallography SISC IAS V8.0 image analysis software. The grain size of prior α phase in different measured points is shown in Fig.4. From Fig.4, it can be seen that the effect of different deformation regions on the grain size is not significant. Therefore, the grain size of prior α phase in each specimen is calculated by the average values of 8 visual fields.

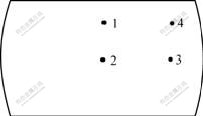
Fig.3 Distribution of measured points in specimen

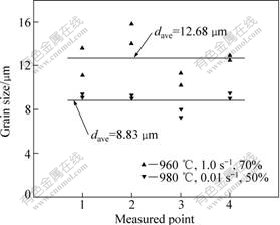
Fig.4 Grain size of prior α phase in different measured points

3 Constitutive equation

In this work, a constitutive equation coupling the grain size in the high temperature deformation of Ti60 alloy is given by[20-21]

σ=F_sF_g                                      (1)

where σ is the flow stress, MPa; F_s is a function of steady flow stress; and F_g is a factor of the flow stress affected by the grain size.

In Eq.(1), the steady flow stress F_s is given by

F_s? σ_s=f₁{Ln(Z)}                             (2)

f₁(x)=A₀+A₁x+A₂x²+A₃x³                        (3)

x=Ln(Z)                                     (4)

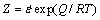                           (5)

where f₁ is a function; Z is the Zener-Hollomon parameter; 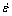 is the strain rate, s^-1; Q is the apparent activation energy for deformation and is 1082.45 kJ/mol in the α+β two-phase region of Ti60 alloy[22]; R is the gas constant, J·mol^-1·K^-1; T is the absolute deformation temperature, K; and A₀, A₁, A₂ and A₃ are the material constants.

In Eq.(1), F_g is written as

F_g? f₂(d)=B₀+B₁(d/d₀)+B₂(d /d₀)²               (6)

where B₀, B₁ and B₂ are functions of Ln(Z) and can be calculated in Eq.(7); d₀ is the initial grain size of prior α phase, ?m; d is the concurrent grain size of prior α phase in the high temperature deformation, μm, and can be predicted by the microstructure model[23]:

f₃(x)=C₀+C₁x+C₂x²+C₃x³                       (7)

where C₀, C₁, C₂ and C₃ are the material constants.

Based on the experimental results, the microstructure model has been established in terms of the fuzzy-neural network theory. The comparison of the calculated with the experimental grain size of isothermally compressed Ti60 alloy is shown in Table 1.

Based on the experimental results of Ti60 alloy, the material constants determined by the least square method are given in Table 2 and Table 3[21].

4 Simulation conditions

The finite elements of the billet with quadrilateral mesh are presented in Fig.5. The cylindrical billet is 16 mm in diameter and 24 mm in height. The upper and lower dies are modeled as rigid bodies at a certain temperature. The present constitutive equation is applied to calculate the flow stress in isothermal upsetting process of Ti60 alloy. The simulation conditions and heat-transfer characteristics are listed in Table 4.

A coupling simulation of deformation with heat transfer and microstructure is carried out with the help of SUPERFORM software in the upsetting process of Ti60 alloy according to the schemes presented in the following groups.

1) When the upper die moves at a velocity of 10.0 mm/s, and the shear factor (m) of friction between the dies and the billet is assumed to be constant along the contact surface and is equal to 0.2, the initial temperature of both the billet and the two dies are 900 ℃ and 980 ℃, respectively.

2) When the initial temperature of both the billet and the two dies is 930 ℃, the upper die moves at a
Table 1 Comparison of calculated with experimental grain size

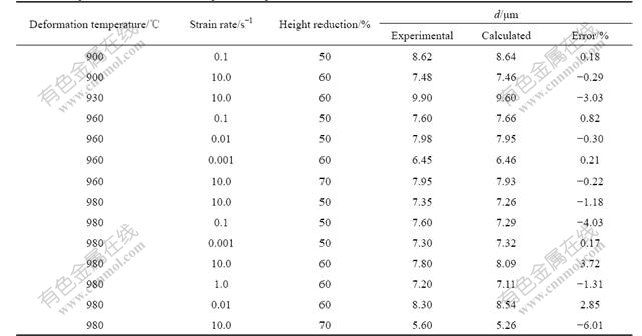
Table 2 Material constants of Ti60 alloy in Eq.(3)

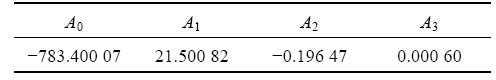
Table 3 Material constants of Ti60 alloy in Eq.(7)

Table 4 Simulation conditions for isothermal upsetting process

Fig.5 FE model of isothermal upsetting and initial meshes of billet

velocity of 1.0 mm/s, and the shear factor (m) of friction between the dies and the billet is assumed to be constant along the surface and is equal to 0.2, the height reductions are 13 mm and 18 mm, respectively.

5 Simulation results and discussion

Applying the present constitutive equation to Ti60 alloy, Ref.[21] has verified that the constitutive equation with high prediction precision can be used to describe the high temperature deformation behavior of Ti60 alloy. Incorporating the constitutive equation into the FE code, a coupled simulation of deformation with heat transfer and microstructure has been carried out in isothermal upsetting process of Ti60 alloy. The effect of processing parameters on the equivalent strain, equivalent stress, the temperature rise and the grain size distribution       has been analysed.

5.1 Effect of deformation temperature

5.1.1 Equivalent strain

Figs.6(a) and (b) show the equivalent strain distribution at the velocity of the upper die of 10.0 mm/s and the shear factor (m) of 0.2 at deformation temperatures of 900 and 980 ℃, respectively. It can be seen from Fig.6 that there is a strain concentration at the edge of the contact surfaces of dies and billet. Moreover, the strain in the central region of the deformed billet is larger than that in the edge region of the deformed billet because of the friction between the dies and billet. The uniformity of the equivalent strain increases with the increase of deformation temperature.

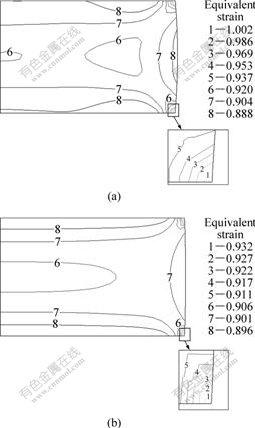
Fig.6 Contours of equivalent strain in upsetting process of Ti60 alloy at different deformation temperatures: (a) 900 ℃;     (b) 980 ℃

5.1.2 Equivalent stress

Figs.7(a) and (b) show the equivalent stress distribution at the velocity of the upper die of 10.0 mm/s and the shear factor (m) of 0.2 at deformation temperatures of 900 and 980 ℃, respectively. It can be seen that the maximum equivalent stress occurs at the edge of the contact surfaces of dies and billet because of strain concentration. The uniformity of the equivalent stress increases with the increase of deformation temperature. The difference between the maximum and the minimum equivalent stress decreases with the increase of deformation temperature. Therefore, an optimal deformation temperature is beneficial to deforming the billet uniformly in this forging process.

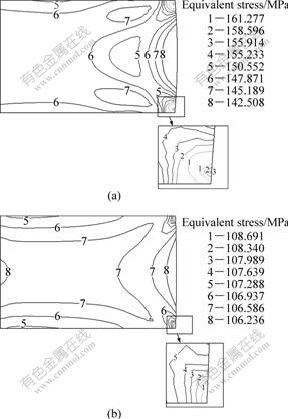
Fig.7 Contours of equivalent stress in upsetting process of Ti60 alloy at different deformation temperatures: (a) 900 ℃;     (b) 980 ℃

5.1.3 Temperature rise

Figs.8(a) and (b) show the actual deformation temperature distribution at the velocity of the upper die of 10.0 mm/s and the shear factor (m) of 0.2 at deformation temperatures of 900 and 980 ℃, respectively. The deformation temperature distribution in the deformed billet is not uniform due to non-uniform deformation in the upsetting process of Ti60 alloy. The deformation temperature of billet decreases continually from the equatorial plane of billet toward the contact surfaces of die and billet. Moreover, it can be found from Fig.8 that the temperature rise decreases from 40 ℃ to 7 ℃ with the increase of deformation temperature.

5.1.4 Grain size

Figs.9(a) and (b) show the grain size distribution of prior α phase at the velocity of the upper die of 10.0 mm/s and the shear factor (m) of 0.2 at deformation temperatures of 900 and 980 ℃, respectively. It can be

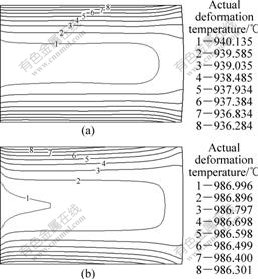
Fig.8 Contours of actual deformation temperature in upsetting process of Ti60 alloy at different deformation temperatures: (a) 900 ℃; (b) 980 ℃

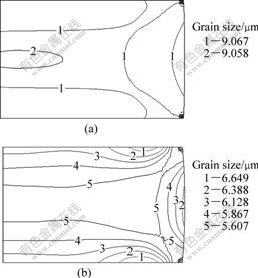
Fig.9 Contours of grain size in upsetting process of Ti60 alloy at different deformation temperatures: (a) 900 ℃; (b) 980 ℃

seen that the grain size decreases with the increase of deformation temperature because the high deformation temperature promotes more phase transformation from α to β, resulting in the decrease of grain size. Moreover, the grain size in the central region of the deformed billet is less than that near the regions of contact surface of the upper and lower dies because of the larger deformation.

5.2 Effect of height reduction

5.2.1 Equivalent strain

Figs.10(a) and (b) show the equivalent strain distribution at the deformation temperature of 930 ℃ and the velocity of the upper die of 1.0 mm/s with height reductions of 13 and 18 mm, respectively. It can be seen that the non-uniformity of equivalent strain increases with the increase of height reduction. In the early stage of this upsetting process, the maximum strain lies in the central region of the deformed billet, then moves towards around with the increase of height reduction.

Fig.10 Contours of equivalent strain in upsetting process of Ti60 alloy with different height reductions: (a) 13 mm; (b) 18 mm

5.2.2 Equivalent stress

Figs.11(a) and (b) show the equivalent stress distribution at the deformation temperature of 930 ℃ and the velocity of the upper die of 1.0 mm/s with different height reductions of 13 and 18 mm, respectively. From Fig.11, it can be seen that the equivalent stress increases with the increase of height reduction. The maximum equivalent stress is at the edge of the contact surfaces of dies and billet because of strain concentration. Moreover, the non-uniformity of equivalent stress increases with the increase of height reduction. The difference between the maximum and the minimum equivalent stress increases with the increase of height reduction.

5.2.3 Temperature rise

Figs.12(a) and (b) show the actual deformation temperature distribution at the deformation temperature of 930 ℃ and the velocity of the upper die of 1.0 mm/s with height reductions of 13 and 18 mm, respectively. As seen in Fig.12, the deformation temperature rise increases with the increase of height reduction. The maximum actual deformation temperature is exhibited in the central region of billet because of the deformation induced heat effect, whilst that near the contact surface of dies and billet is lower because of the smaller deformation and higher heat transfer of contact with the dies.

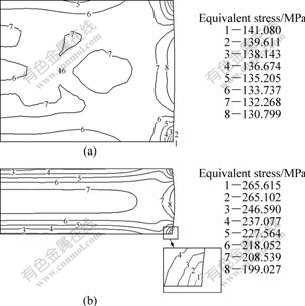
Fig.11 Contours of equivalent stress in upsetting process of Ti60 alloy with different height reductions: (a) 13 mm; (b) 18 mm

Fig.12 Contours of actual deformation temperature in upsetting process of Ti60 alloy with different height reductions: (a) 13 mm; (b) 18 mm

5.2.4 Grain size

Figs.13(a) and (b) show the grain size distribution at the deformation temperature of 930 ℃ and the velocity of the upper die of 1.0 mm/s with two height reductions of 13 and 18 mm, respectively. In the early stage illustrated in Fig.13(a), the small grain size appears near the contact region of the billet and dies, whilst the large grain size appears in the centre of billet, resulting from the non-uniform deformation temperature. The maximum actual deformation temperature is exhibited in the centre of billet because of the deformation induced heat effect. The higher actual deformation temperature promotes the grain growth. Therefore, the small grain size appears in the above-mentioned region. However, the small grain size in the final stage illustrated in Fig.13(b) appears in the centre of billet, resulting from the larger deformation. Moreover, it can be seen that the grain size and the non-uniformity of grain size increase with the increase of height reduction.

Fig.13 Contours of grain size in upsetting process of Ti60 alloy with different height reductions: (a) 13 mm; (b) 18 mm

5.3 Verification

To confirm the validity of finite element simulation in isothermal upsetting process of Ti60 alloy, a series of compression tests were carried out. Isothermal compression at a constant strain rate was conducted at a Thermecmaster-Z simulator. The specimens prior to isothermal compression were heated and held for 3.0 min at a deformation temperature of 980 ℃ so as to obtain a uniform deformation temperature. After isothermal compression, the specimens were cooled in air to room temperature. The isothermally compressed Ti60 alloy specimens were axially sectioned and prepared using standard metallographic techniques.

The comparison of the calculated with the experimental grain size is shown in Table 5. The maximum difference between the calculated and the experimental grain size of prior α phase is -10.79%. This shows that the calculated results are in good agreement with the experimental data.

Table 5 Comparison of calculated with experimental grain size

6 Conclusions

1) The equivalent strain, the equivalent stress, the temperature rise and the grain size distributions in the upsetting process of Ti60 alloy have been calculated through the coupling FE simulation with the grain size.

2) The uniformity of equivalent strain and equivalent stress increases with the increase of deformation temperature; however, the temperature rise and the grain size decrease with the increase of deformation temperature.

3) The non-uniformity of equivalent strain, equivalent stress, temperature field and grain size increases with the increase of height reduction. The calculated grain size using FE simulation is in a good agreement with the experimental one.

References

[1] LIN S Y. Upsetting of a cylindrical specimen between elastic tools [J]. J Mater Process Technol, 1999, 86(1/3): 73-80.

[2] WANG Lian-sheng, CAO Qi-xiang, LIU Zhuang. Numerical simulation and experimental verification of microstructure evolution in a 3-dimensional hot-upsetting process [J]. J Mater Process Technol, 1996, 58(2/3): 331-336.

[3] NA Y S, YEOM J T, PARK N K, LEE J Y. Simulation of microstructures for alloy 718 blade forging using 3D FEM simulator [J]. J Mater Process Technol, 2003, 141(3): 337-342.

[4] LI Xiao-li, LI Miao-quan. FE simulation for the forging process of TC6 alloy disc utilising a microstructural model [J]. Mater Charact, 2005, 55(4/5): 362-370.

[5] ZHANG Shi-hong, SUN Cheng, WANG Zhong-tang. Finite element simulation on press forging of magnesium alloy AZ31 sheets [J]. Trans Nonferrous Met Soc China, 2008, 18(1): 269-272.

[6] GAO Tao, YANG He, LIU Yu-li, LIU Jun. Influence of processing parameters on microstructure evolution during blade precision forging process of titanium alloy [J]. Rare Metal Mater Eng, 2005, 34(5): 781-785.

[7] SELLARS C M, MCTEGART W J. On the mechanism of hot deformation [J]. Acat Metall, 1966, 14(9): 1136-1138.

[8] SELLARS C M, ZHU Q. Microstructural modelling of aluminium alloys during thermomechanical processing [J]. Mater Sci Eng A, 2000, 80(1): 1-7.

[9] YADA H, SENUMA T. Resistance to hot deformation of steel [J]. J Jpn Soc Technol Plasticity, 1988, 27: 33-44.

[10] KARHAUSEN K, KOPP R. Model for integrated process and microstructure simulation in hot forming [J]. Steel Res, 1992, 63(6): 247-256.

[11] SENUMA T, SUEHIRO M, YADA H. Mathematical models for predicting microstructural evolution and mechanical properties of hot strips [J]. ISIJ Int, 1992, 32(3): 423-432.

[12] DING R, GUO Z X. Microstructural modelling of dynamic recrystallization using an extended cellular automaton approach [J]. Comput Mater Sci, 2002, 23(1/4): 209-218.

[13] RADHAKRISHNAN B, SARMA G B, ZACHARIA T. Modeling the kinetics and microstructural evolution during static recrystallization—Monte Carlo simulation of recrystallization [J]. Acta Mater, 1998, 46(12): 4415-4433.

[14] LI Xiao-li, LI Miao-quan. Microstructure evolution model based on deformation mechanism of titanium alloy in hot forming [J]. Trans Nonferrous Met Soc China, 2005, 15(4): 749-753.

[15] SEMIATIN S L, SOPER J C, SUKONNIK I M. Short-time Beta grain growth kinetics for a conventional titanium alloy [J]. Acta Mater, 1996, 44(5): 1979-1986.

[16] KIM J K, SEMIATIN S L, LEE C S. Constitutive analysis of the high-temperature deformation of Ti-6Al-4V with a transformed microstructure [J]. Acta Mater, 2003, 51(18): 5613-5626.

[17] SALEM A A, KALIDINDI S R, SEMIATIN S L. Strain hardening due to deformation twinning in α-titanium: Constitutive relations and crystal-plasticity modeling. [J]. Acta Mater, 2005, 53(12): 3495-3502.

[18] LUO Jiao, LI Miao-quan, LI Hong, YU Wei-xin. High temperature deformation behavior of TC4 titanium alloy and its flows stress model [J]. The Chinese Journal of Nonferrous Metals, 2008, 18(8): 1395-1401. (in Chinese)

[19] KOBAYASHI S, OH S I, ALTAN T. Metal forming and the finite element method [M]. New York: Oxford University Press, 1989: 151-159.

[20] LI Miao-quan, XIONG Ai-ming, WANG Hai-rong, SU Shao-bo, SHEN Li-chuang. Deformation behavior and new constitutive equation utilising the grain size of commercial TC6 titanium alloy [J]. Mater Sci Technol, 2004, 20(10): 1261-1265.

[21] LUO Jiao, LI Miao-quan, HU Yi-qu. A constitutive equation coupled the grain size at the high temperature deformation of Ti60 alloy [J]. Mater Sci Forum, 2007, 561/565: 155-158.

[22] LI Miao-quan, PAN Hong-si, LIN Ying-ying, LUO Jiao. High temperature deformation behavior of near Alpha Ti-5.6Al-4.8Sn-2.0Zr alloy [J]. J Mater Process Technol, 2007, 183(1): 71-76.

[23] LUO Jiao, LI Miao-quan, HU Yi-qu, FU Ming-wei. Modeling of constitutive relationships and microstructural variables of Ti60 alloy during high temperature deformation [J]. Mater Charact, 2008, 59(10): 1386-1394.

(Edited by YANG Bing)

Foundation item: Project(KP200905) supports by the Fund of the State Key Laboratory of Solidification Processing in Northwestern Polytechnical University, China

Corresponding author: LI Miao-quan; Tel: +86-29-88491478; Fax: +86-29-88492642; E-mail: honeymli@nwpu.edu.cn

DOI: 10.1016/S1003-6326(09)60225-9