一种易于工程实现的九加速度计测姿方法
王晓丽，周浔
(装甲兵工程学院 控制工程系，北京，100072)
摘要：通过对无陀螺捷联惯性导航系统的测量原理进行分析，从易于工程实现的角度，设计了一种基于九加速度计的无陀螺惯导系统的配置方案，研究基于这种配置方案的姿态测量方法。
关键词：无陀螺捷联惯导系统；姿态测量；加速度计
中图分类号：V249.32 文献标志码：A 文章编号：1672-7207(2011)S1-0483-03
A attitude measurement method of nine-accelerometer
WANG Xiao-li, ZHOU Xun
(Department of Control Engineering, Academy of Armored Force Engineering, Beijing 100072, China)
Abstract: Based on the non-gyro inertial navigation system, the measurement principle was analyzed, and a kind of nine- accelerometer configuration scheme was designed which is easy to engineering realization. The attitude measurement method of this accelerometer configuration scheme was researched.
Key words: GFSINS; attitude measurement; accelerometer
近年来，无陀螺捷联惯导系统受到了广泛和深入地研究，并取得了一定的成果。基于无陀螺捷联惯导系统，提出了多种配置方案、理论算法。目前，无陀螺捷联惯导系统按使用加速度计元件的数目可分为六加速度计、九加速度计和十二加速度计等几大类[1-2]，每一类都可以有不同的加速度计配置方式。加速度计是一种应用十分广泛的惯性传感器，它可以用来测量运动系统的加速度。无陀螺捷联惯导系统就是指惯性测量系统中不用陀螺测量角速度，只用加速度计作为测量敏感元件的惯性系统，载体的角速度和姿态都从加速度计输出获取[3]。无陀螺捷联惯导系统适用于大动态范围、导航时间较短的载体的惯性导航，其优点是成本低、功耗低、寿命长、可靠性高等[4]。随着新型高精度加速度计的出现和滤波技术的发展，可达到较高的导航精度。本文作者研究了一种基于九加速度计的姿态测量原理，通过在载体运动中对其运动的加速度情况进行分析，解算出载体的姿态。
1 惯性测量原理
惯导系统利用惯导仪表(陀螺仪和加速度计)测量运动载体在惯性空间中的角运动和线运动，根据载体运动微分方程组实时精确地解算出载体的位置、速度和姿态角。
要求解任意时刻载体的姿态，需要建立当地水平坐标系(r系)和载体坐标系(b系)。当地水平坐标系也称为NED坐标系、地理坐标系或惯性直角坐标系，其y轴指向当地北子午线，x轴与y轴垂直指向东，z轴与x和y正交构成右手坐标系。载体坐标系的y轴与载体运动方向的中心线(主轴)重合，正向指向载体的运动方向，x轴垂直y轴指向载体右侧，z轴与x和y正交构成右手坐标系，坐标系的原点可根据具体需要设定。载体在坐标系中的运动如图1所示。
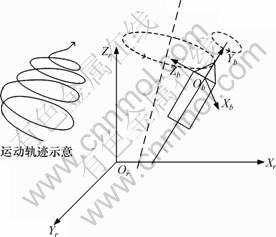
图1 载体在坐标系中的运动示意图
Fig.1 Carrier movement in the coordinate
2 加速度计配置方案
对于无陀螺捷联惯导系统，必须利用至少6个加速度计来测量载体的质心运动和绕质心的转动，且为了测量绕质心的转动，加速度计必须安装在载体非质心处[5-6]。载体角速度的解算利用了加速度计的杆臂效应，杆臂距离越长，加速度计测量信号就越强，噪声引起的测量误差也就越小。一般来讲，加速度计安装点离载体质心越远，测量精度越高[7-8]。九加速度计无陀螺捷联惯导系统，除了能得到描述载体运动所需的6个独立参量外，还有3个冗余量，通过这3个冗余信息，可计算出载体姿态角速度的部分误差，并对其进行补偿，提高系统的精度。
本文从易于工程实现的角度考虑，为精确测定载体的姿态，将9个加速度计安装在载体顶部截面的中心位置。加速度计的安装位置为：在载体坐标系的原点放1个三轴加表，以原点为对称中心，在每个坐标轴上对称放置2个加表，加表的敏感轴与坐标轴一致(如图2所示)。
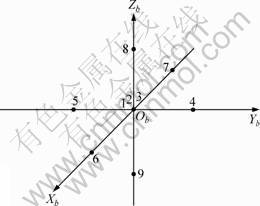
图2 加速度计安装位置示意图
Fig.2 Accelerometer installation location schemes
3 姿态测量原理
3.1 初始姿态确定
在发射前，已知载体的精确位置。利用坐标系间的转换公式，可以得出初始时刻载体的姿态。设当地水平坐标系为r系，载体坐标系为b系，任意矢量r从当地水平坐标系至载体坐标系的转换关系(比例因子取1)为：
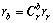(1)
这里的方向余弦矩阵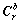
可以用欧拉角中的偏航角、俯仰角和横滚角表示。设定水平坐标系先绕z轴旋转，即偏航角Ψ；再绕x轴旋转，即俯仰角θ；最后绕y轴旋转，即横滚角φ。得到：
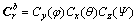(2)
将式(2)展开得：
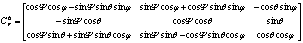(3)
由式(3)得欧拉角：
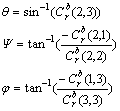(4)
载体发射前处于静止状态，所以，所有加速度计的值均为0。重力的方向始终垂直向下，因而可以测定发射前重力加速度在载体坐标系中的矢量表示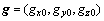
。
3.2 姿态解算
在载体运动中的某时刻t，对其运动的加速度情况进行分析。在载体坐标系中，对载体所受到的加速度进行分解，分为Xb，Yb，Zb 3个坐标轴的3个分量。选取Xb轴作为研究对象，载体在此坐标轴上安装的3个角速度计(编号分别为2，6，7)所受到的加速度分析如图3所示。
图3所示为Xb方向载体运动所受到的加速度。设载体自转的角速率为ω′，公转角速率为ω；安装在载体自转中心的加表2与公转轴的距离为Rx，以2为中心对称安装的加表6和7与2点的距离为R。
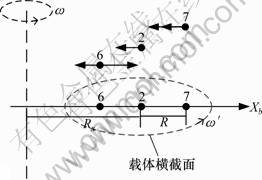
图3 Xb轴方向所受加速度示意图
Fig.3 Schematic diagram of Xb-axis acceleration
因为载体的运动为变速率旋转运动，所以其处于非平衡运动状态。加表6所测得的加速度为自转向心加速度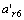
，公转向心加速度
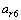，重力加速度在Xb轴的分量
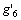，其他使载体平动的外力作用下的平动加速度在Xb轴的分量
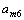；加表7所测得的加速度为自转向心加速度
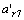，公转向心加速度
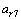，重力加速度在Xb轴的分量
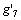，其他使载体平动的外力作用下的平动加速度在Xb轴的分量
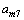；因加表2位于自转轴心上，自转加速度为0，其所测得的加速度为公转向心加速度
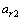，重力加速度在Xb轴的分量
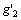，其他使载体平动的外力作用下的平动加速度在Xb轴的分量
。
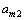因运动载体为刚体，所以
，
，
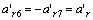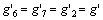(5)
向心加速度与角速率的关系：
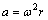(6)
因此，加表6测得的加速度为：
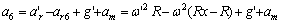(7)
同理，加表7和加表2测得的加速度分别为：
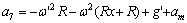(8)
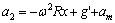(9)
同理可得另外2个坐标轴上的加速度分量，经过捷联矩阵变换成沿地理坐标系的分量，再经过一次积分和二次积分就可以分别得到载体的速度和位置。
4 结论
无陀螺捷联惯导系统克服了陀螺仪带来的成本高、机动性差和难以小型化等缺点，特别适用于战术导弹等大动态范围且工作时间短的载体，具有良好的应用前景。本文采用基于九加速度计的配置方案进行载体姿态解算，也较易于工程实现。
参考文献：
[1] hen J H, Lee S C, DeBra D B. Gyroscope free strap-down inertial measurement unit by six linear accelerometers[J]. Journal of Guidance, Control and Dynamics, l994, 17(2): 286-290.
[2] 刘涛, 赵国荣, 王丕毅, 等. 一种无陀螺捷联惯导系统角速度解算组合算法[J]. 海军航空工程学院学报, 2009, 24(1): 43-46.
LIU Tao, ZHAO Guo-rong, WANG Pi-yi, et al. A combining algorithm of calculating angular-velocity in GFSINS[J]. Journal of Naval Aeronautical and Astronautical University, 2009, 24(1): 43-46.
[3] 赵国荣, 陈穆清. 一种用于九加速度计GFSINS的姿态角速度辅助算法[J]. 系统仿真学报, 2007, 17(14): 3350-3353.
ZHAO Guo-rong, CHEN Mu-qing. Attitude angular velocity algorithm for nine-accelerometer GFSINS[J]. Journal of System Simulation, 2007, 17(14): 3350-3353.
[4] 周红进, 许江宁, 覃方君. 一种新的基于加速度计的无陀螺捷联惯性导航系统设计与实现[J]. 仪器仪表学报, 2008, 29(7): 1499-1502.
ZHOU Hong-jin, XU Jiang-ning, QIN Fang-jun. Design and realization of novel gyro-free strapdown inertial navigation system based on accelerometer[J]. Chinese Journal of Scientific Instrument, 2008, 29(7): 1499-1502.
[5] 史震. 无陀螺捷联惯导系统中加速度计配置方式[J]. 中国惯性技术学报, 2002, 10(1): 15-19.
SHI Zhen. Accelerometer allocation scheme in gyroscope free strapdown inertial navigation system[J]. Journal of Chinese Inertiai Technology, 2002, 10(1): 15-19.
[6] 李奕恒, 马铁华, 裴东兴. 无陀螺导弹姿态测试系统的设计[J]. 传感器与微系统, 2008, 27(5): 96-98.
LI Yi-heng, MA Tie-hua, PEI Dong-xing. Design of non-gyroscope missile posture test system[J]. Transducer and Microsystem Technologies, 2008, 27(5): 96-98.
[7] 汪小娜, 王树宗, 朱华兵, 等. 基于加速度计的无陀螺捷联惯性制导系统设计[J]. 武汉理工大学学报: 交通科学与工程版, 2007, 31(6): 1010-1013.
WANG Xiao-na, WANG Shu-zong, ZHU Hua-bing, et al. Study on gyroscope free strap-down inertial guidance system based on accelerometers[J]. Journal of Wuhan University of Technology: Transportation Science ＆ Engineering, 2007, 31(6): 1010-1013.
[8] 徐涛, 温东, 孙晓磊. 基于加速度计和磁强计的方位测量与校正技术研究[J]. 仪器仪表学报, 2009, 30(10): 2018-2022.
XU Tao, WEN Dong, SUN Xiao-lei. Research on azimuth measurement and correction technique with accelerometer and magnetometer[J]. Chinese Journal of Scientific Instrument, 2009, 30(10): 2018-2022.
(编辑 赵俊)
收稿日期：2011-04-15；修回日期：2011-06-15
通信作者：王晓丽(1976-)，女，河南周口人，讲师，从事惯性导航与制导理论研究；电话：15011338400；E-mail：zgysunny@163.com
