DOI: 10.11817/j.issn.1672-7207.2016.04.035
裂缝面非均匀流入的低渗透油藏压裂水平井非稳态产量计算
曾凡辉,程小昭,郭建春
(西南石油大学 油气藏地质及开发工程国家重点实验室,四川 成都,610500)
摘要:基于瞬时点源函数和叠加原理,考虑压裂水平井裂缝段产量非均匀流入、裂缝内变质量以及多裂缝间的相互干扰,采用空间和时间离散技术,建立低渗透油藏压裂水平井储层渗流和裂缝流动相耦合的非稳态产量计算模型。研究结果表明:以往将裂缝考虑为无限导流或者将裂缝考虑为均匀产量流入的平面径向流假设使得计算结果比实际产量偏高;在早期非稳态流动阶段,裂缝产量在井筒附近出现局部峰值,并且储层渗透率越高,裂缝导流能力越小,峰值越明显;在拟稳态生产阶段,低导流能力裂缝的流量分布趋于均匀,而高导流能力裂缝内流量分布进一步非均匀化;为了获得压裂水平井的最佳生产效果,存在与储层渗透率相匹配的最优裂缝导流能力。
关键词:压裂水平井;点源函数;非均匀流入;非稳态
中图分类号:TE112.222 文献标志码:A 文章编号:1672-7207(2016)04-1353-06
Calculation of unsteady productivity of fractured horizontal wells
ZENG Fanhui, CHENG Xiaozhao, GUO Jianchun
(State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,
Southwest Petroleum University, Chengdu 610500, China)
Abstract: A dynamic model that coupled seepage in reservoir and fluid flow in fractures was built using spatial and time discrete technique in fractured horizontal well, taking into account the non-uniform flow rate of fracture segments, fracture inner variable mass flow and fracture segments mutual interference, and the solution method was also given. The results show that when regarding the inflow to the fractures as uniform and neglecting the pressure drop in the fractures, there may be higher deviation in productivity calculation of fractured horizontal well compared with actual production. In the early stage of unsteady flow, the fracture segments closer to the horizontal wellbore, the higher production of the segments, the smaller the fracture conductivity and the higher the peak. In the quasi stable production stage, the flow rate distribution of the low-conductivity fractures tends to be more uniform, while further non-uniform of the high-conductivity fractures. In order to get the best production of fractured horizontal well, there exists the optimal fracture conductivity matching with the fracture permeability.
Key words: fractured horizontal well; point source function; non-uniform flow; transient state
储层中由于流体采出或注入引起的压力响应可由渗流偏微分方程表示,求解压裂井储层渗流的实质就是求解含有不同裂缝的地层渗流模型问题。采用瞬时点源函数是求解储层渗流问题的有效方法,将瞬时点源解关于时间叠加后就能得到连续点源解[1-3]。在利用源函数求解压裂水平井的产量问题时,涉及对于存在裂缝的储层内渗流和裂缝内流动时2个基本过程的描述。在描述储层内渗流过程时,一般是将压裂水平井的裂缝处理成有限个点汇,利用叠加原理或积分变换, 建立多个点汇同时存在时在裂缝尖端的压力响应[4-13]。对于裂缝内的流动描述,目前主要的处理方法是:1) 假设流体沿裂缝面均匀流入裂缝[14-18];2) 流体在裂缝内满足平面径向流的流动规律流入到水平井筒[4, 7-13]。该方法的缺陷在于将储层渗流和裂缝内流动分成了2个相对独立的过程,并且没有考虑流体沿裂缝面非均匀不断流入裂缝的实际情况。因此,尽管目前的压裂水平井产量预测模型考虑了储层渗流和裂缝内流动,但对于流体在储层和裂缝内流动的耦合描述并不全面,导致传统压裂水平井产量模型的计算结果与实际情况存在较大差别。本文作者针对传统压裂水平井产量预测模型的不足,将压裂水平井多裂缝离散为有限长度的点源,基于瞬时点源函数和叠加原理,采用空间和时间离散技术,综合考虑裂流量沿裂缝面非均匀流入、裂缝内变质量流动以及多裂缝的相互干扰情况,建立压裂水平井产量预测模型,通过实例验证模型的可靠性,并分析影响压裂水平井裂缝产量分布的因素。
1 数学模型的建立
在建立压裂水平井的产量计算模型前,进行以下基本假设:储层上下封闭、水平无限大等厚均质;油藏流体微可压缩,在储层中为等温非稳定达西渗流,忽略重力的影响;储层流体沿裂面非均匀流入裂缝,再经过裂缝流入到水平井筒;同一条裂缝宽度恒定,流体在裂缝内遵循达西流动规律;各条裂缝的长度和宽度可以相等或者不相等;水平井筒具有无限导流能力,即忽略流体在水平井筒内的压力降落。
1.1 油藏渗流模型
考虑无限大油藏中的1口水平井模型见图1(上顶下底封闭),水平井被分成若干段,油藏中流体首先流向裂缝再流向水平井筒。水平井半径为rw,长度为L,井在油藏中心位置坐标为(x0, y1, z0)~(x0, y2, z0)(其中,y1和y2分别表示水平井筒的起点和终点),且与y轴平行。油藏均质各向同性,厚度为h,孔隙度为φ,渗透率K为常数;在水平井段压裂出N条垂直裂缝,裂缝间距、裂缝长度和裂缝宽度可以相等也可以不相等,第k条裂缝单翼缝长为xfk,裂缝宽度为wfk;油藏初始压力为常数pi。
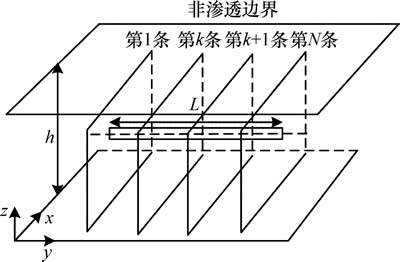
图1 上顶下底封闭无限大油藏压裂水平井模型
Fig. 1 Physical model of fractured horizontal well in infinite reservoir
由于压裂裂缝贯穿油层,因此,无限大地层压裂水平井整个系统的流动可简化为平面油藏内的径向流动,裂缝可简化为一线(点)汇[16]。为了便于求解,将任意1条裂缝单翼分成ns段,这样就将裂缝离散成了ns个裂缝线汇微元段(见图2)。每个微元段长为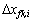 (1≤i≤ns),可将每一微元裂缝段等效为1口直井。定井底流压生产时油井产量随时间不断变化,但若将时间间隔取得很小,则可以近似地认为该段时间内产量为定值,地层中任意1点压降可以按照无限大均匀地层线汇定产量压降公式计算[7, 17]。在平面直角坐标系下(见图2),微元段M(xfk,i,ykf)(产量为qfk,i)对微元段O(xfk+1,j,yfk+1)在生产时间t后的压降公式为[7-8]
(1≤i≤ns),可将每一微元裂缝段等效为1口直井。定井底流压生产时油井产量随时间不断变化,但若将时间间隔取得很小,则可以近似地认为该段时间内产量为定值,地层中任意1点压降可以按照无限大均匀地层线汇定产量压降公式计算[7, 17]。在平面直角坐标系下(见图2),微元段M(xfk,i,ykf)(产量为qfk,i)对微元段O(xfk+1,j,yfk+1)在生产时间t后的压降公式为[7-8]
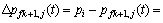
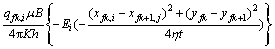 (1)
(1)
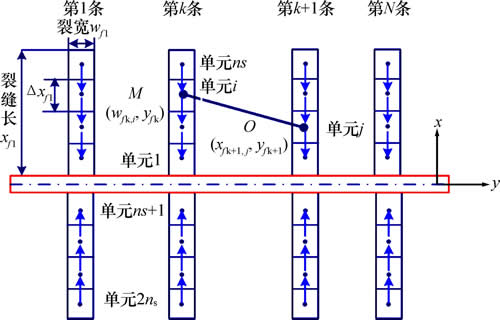
图2 二维平面分段及离散化示意图
Fig. 2 Sectional schematic of fracture and reservoir node in model
当裂缝k上存在ns个微元段时,根据叠加原理,可以得到第k条裂缝上ns个微元段同时生产时对O点的压力响应;类似地,也能得到N条裂缝同时生产时在O点的压力降落方程:
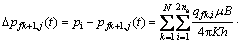
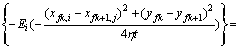
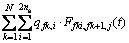 (2)
(2)
式中:pi为原始地层压力,MPa;pfk+1,j为第k+1条裂缝的第j微元段井壁处压力,MPa;N为压裂水平井裂缝条数,条;ns为裂缝单翼线汇数;qfk,i为第k条裂缝的第i微元段产量,m3/s;(xfk,i,yf,k)为第k条裂缝的第i微元段中心坐标;(xfk+1,j,yf,k+1)为第k+1条裂缝的第j微元段中心坐标;μ为原油黏度,mPa.s;B为无因体积系数次;K为油藏渗透率,10-3 μm2;h为储层厚度,m;η为导压系数,η=K/(μcf);c为综合压缩
系数,MPa-1;f为岩石孔隙度;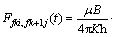
 ,表示微元
,表示微元
(xfk,i,yf,k)对微元(xfk+1,j,yf,k+1)的影响作用;k为裂缝编号;i和j为微元编号。式(2)是利用空间离散和叠加原理建立的考虑压裂水平井各线汇相互干扰的渗流方程。
为了利用式(2)计算压裂水平井非稳定阶段的产量,可以通过时间叠加原理来得到。以微元段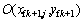 的压降计算为例,在t=Δt时刻,可以得到
的压降计算为例,在t=Δt时刻,可以得到

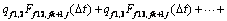
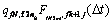 (3)
(3)
当t=nΔt时,利用时间叠加原理,可以得到第n个时间步(t=nΔt)的压力降落方程:
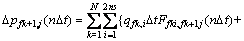
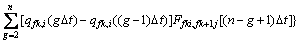 (4)
(4)
针对每一个微元段均可以写出类似的方程。
1.2 裂缝流动模型
假设流体经过裂缝面进入裂缝后向水平井筒的流动为一维线性流动(图3)。为了便于计算,将每个微元段处理成矩形进行计算,裂缝宽度为wfk+1,以计算流体在裂缝中流动时的压力降落。
由达西定律计算第k+1条裂缝第j微元段(点Ofk+1,j)流动到水平井筒(点Ofk+1,0)间的压差为
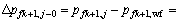
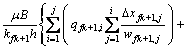
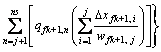 (5)
(5)
式中:Kfk+1为第k+1条裂缝渗透率,10-3μm2;h为储层厚度,m;wfk+1为第k+1第裂缝宽度,m。
式(5)中右边第1项表示第k+1条裂缝第j及之前微元段产量在裂缝内流动时产生的压降;第2项表示第k+1条裂缝第j微元段产量在裂缝内流动时产生的压降。
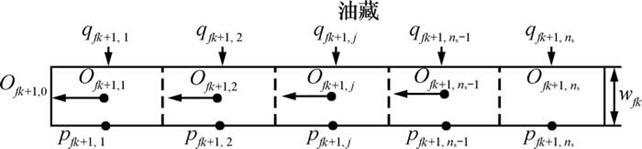
图3 裂缝内流动单元示意图
Fig. 3 Sketch map of flow unit in fracture
1.3 耦合流动模型
油藏流动在裂缝壁面处压力与裂缝流动在裂缝壁面处的压力相等,即可根据观察点Ofk+1,j点压力连续由式(4)和(5)建立压力连续方程;由于考虑井筒无限导流,在定井底流压生产时水平井筒压力为常数,各裂缝与水平井筒相交处Ofk+1,0的压力相等:
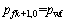 (6)
(6)
式中:pfk+1,0为k+1条裂缝与水平井筒相交处的压力,MPa;pwf为水平井筒井底流压,MPa。联立方程(4)~(6)即可得到第k+1条裂缝第j微元段的油藏-裂缝耦合流动方程,共有N×2ns个。这样,利用空间离散和时间叠加建立压裂水平井的非稳态产量预测新模型。
1.4 求解方法
该模型的求解包括油藏渗流和裂缝内流动2个过程。首先根据压裂水平井基本参数,将裂缝离散成微元段并计算各微元段对观测微元段的压力降落(式(4));计算观测微元段在裂缝内流动的压力损失(式(5));将计算流体在油藏渗流和裂缝内流动的方程联立,由于没有引入新变量,针对每个微元段均能建立1个独立方程,这样就会得到1个含有N×2ns个未知数qfk,i (1≤i≤N×2ns),N×2ns个方程可封闭求解的方程组。由于未知数间满足线性变化关系,采用Gauss全主元消去法求解该方程组。
2 计算实例及敏感性分析
为了研究压裂水平井产量模型的可靠性以及生产时间、储层渗透率、裂缝导流能力等对压裂水平井流入动态的影响,对某油田1口实际压裂水平井进行计算。基础参数如下:油藏厚度为12 m,地层渗透率为0.003 5 μm2,地层孔隙度为10%,水平井长度为400 m,井筒半径为0.12 m,体积系数为1.084,原油黏度为8 mPa·s,原油密度为870 kg/m3,压缩系数为0.000 35 MPa-1,生产压差为5 MPa,裂缝宽度为5.0 mm,裂缝单翼缝长为75 m,渗透率为30 μm2,压裂后在水平井筒上形成4条均匀分布的垂直裂缝。
2.1 模型的验证
分别按照本文建立的裂缝有限导流非均匀流量分布模型、裂缝有限导流均匀流量模型[7-8]以及裂缝无限导流模型计算的对比结果见表1。从表1可以看出:本文模型的预测结果从开始生产到拟稳定生产阶段与实际产量最接近, 验证了模型的可靠性,而裂缝无限导流模型的计算结果远高于实际结果,表明不能忽略裂缝内压力损失的影响;裂缝均匀流量模型在生产初期的计算结果高于实际结果,而在生产后期差别变小。
2.2 水平井产量与时间的关系
图4所示为水平井产量与时间的关系曲线。从图4可以看出:刚开始生产时流动状态很不稳定,产量下降很快。这是因为压力波还未扩散到大部分流动区域,流体仅从裂缝周围的基岩向裂缝线性流动,此时处于早期非稳态阶段;随着时间增加,压力波逐渐向外扩散,产量趋向于定值,流动达到拟稳态阶段。从不同位置裂缝的产量看,在生产初期,裂缝间还没有发生干扰,各条裂缝产量基本相等(裂缝1和4产量为6.151 m3/d,裂缝2和3产量为6.054 m3/d);而在拟稳态阶段(t=120 d),由于裂缝间的相互干扰,2条中间裂缝之间流动区域的产量下降很快, 而外部裂缝具有更大的泄油区域,使得水平井段两端裂缝的产量(裂缝1和4为1.883 m3/d)高于内部裂缝的产量(裂缝2和3为1.320 m3/d)。
图5所示为3种模型裂缝1在不同生产时间下(t为0.1 d和100 d)的流量分布。本文模型考虑了裂缝无限导流以及流量非均匀分布,在生产初期(t=0.1 d),裂缝中间产量高两端产量低,裂缝产量在井筒附近出现局部峰值。这是因为此时压力还没有大范围扩散,地层各点压力基本上为原始地层压力,而裂缝内存在压力损失,越靠近井筒附近,生产压差越大,使得裂缝产量越高;随着生产时间增加(t=100 d),峰值显著程度降低,裂缝的产量分布趋于均匀,裂缝内产量分布近似为双“U”型分布,这是压裂水平井裂缝段之间存在相互干扰所致[18]。无限导流模型由于没有忽略裂缝内的压力损失,在生产初期(t=0.1 d)裂缝的流量为“U”型分布,裂缝两端流量较高;随着生产时间增加(t= 100 d),由于裂缝段内的干扰增强,裂缝内流量非均匀分布进一步加强,这与文献[16]中的规律一致。
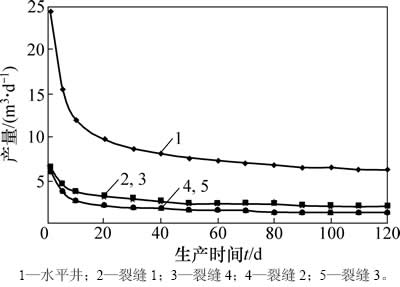
图4 水平井产量与时间的关系
Fig.4 Relationship between daily production and time
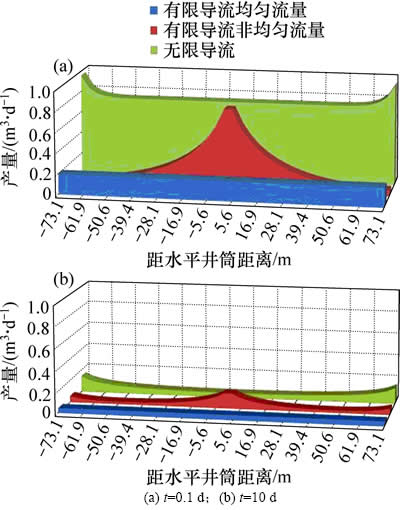
图5 裂缝流量分布与时间的关系
Fig. 5 Relationship between production distribution and time for different models
表1 不同模型产量计算结果对比
Table 1 Comparison of Simulated solution and actual productivity m3/d

2.3 裂缝流量分布与时间的关系
图6所示为裂缝1在生产不同时刻下的裂缝流量分布结果。从图6可以看出:在生产初期(t=0.1 d),由于裂缝之间还没有产生干扰,距离水平井筒段越近裂缝内压力越低,产量主要是从裂缝中间段产出;随着生产时间增加,压力逐渐向外传播和产生干扰,使得裂缝中间段产量逐渐降低,而裂缝两端的产量逐渐上升(t=10 d);随着时间进一步增加,裂缝上的产量分布趋于稳定和均匀,基本上呈现出均匀产液的特征(t=100 d)。
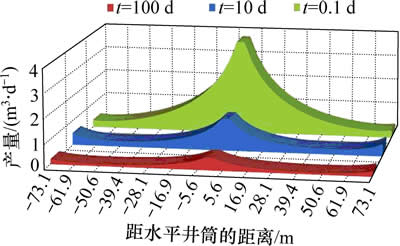
图6 裂缝流量与裂缝位置的关系
Fig. 6 Relationship between flow distribution and distance
2.4 裂缝流量分布与储层渗透率的关系
图7所示为压裂水平井第1条裂缝的流量分布与储层渗透率的关系。从图7可以看出:在生产初期(t=0.1 d),由于地层渗透率越高产量越大,裂缝内的压力损失越显著,井筒附近裂缝产量峰值越明显,裂缝上的产量分布越不均匀;随着地层渗透率降低,裂缝面上的产量分布越均匀。随着生产时间增加,裂缝产量分布趋于均匀,并且储层渗透率越低,裂缝产量越均匀。
2.5 裂缝流量与裂缝导流能力的关系
图8所示为压裂水平井裂缝1产量分布与裂缝导流能力的关系。从图8可以看出:对于一定渗透率的储层,在生产初期(t=0.1 d),裂缝产量在井筒附近出现局部峰值,并且裂缝导流能力越小,峰值越显著;随着时间增加,低导流能力裂缝(kf=3 μm2·cm,kf= 15 μm2·cm)的产量从裂缝中间向两端转移,裂缝上的产量趋于均匀和稳定;而高导流能力裂缝(kf=30 μm2·cm) 的产量从裂缝两端向中间转移,进一步加剧了裂缝产量的非均匀分布。
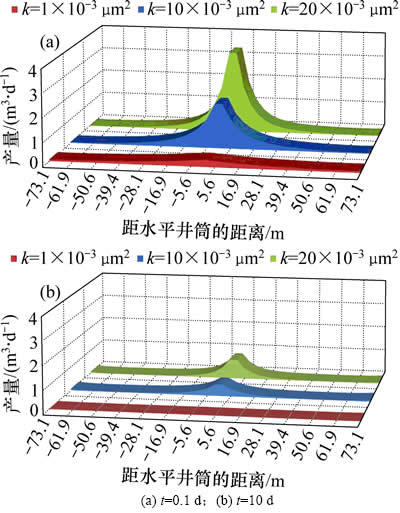
图7 裂缝流量分布与储层渗透率的关系
Fig. 7 Relationship between flow distribution and formation permeability
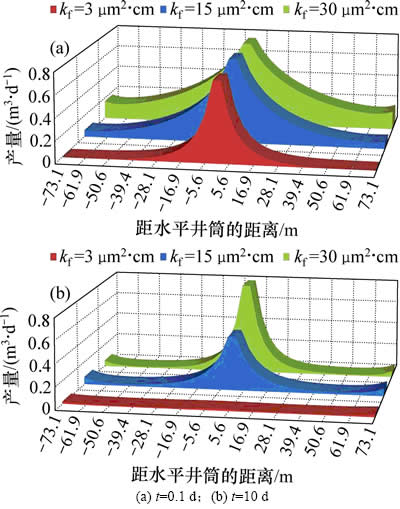
图8 裂缝流量分布与裂缝导流能力的关系
Fig. 8 Relationship between production distribution and fractures conductivity
3 结论
1) 基于瞬时点源函数和叠加原理,采用空间和时间离散技术,考虑裂缝上的非均匀流入以及裂缝内摩阻变化,建立压裂水平井非稳态产量计算新模型。该方法实用性强,计算方法简单,求解稳定可靠,能够计算压裂水平井、裂缝以及微元段的产量。
2) 裂缝的产量分布与生产时间、储层渗透率以及裂缝导流能力等密切相关。在生产初期,产量主要是从裂缝中间段产出,裂缝产量在井筒附近出现局部峰值,呈现出非均匀分布特征,并且储层渗透率越高,裂缝导流能力越小,峰值越明显;在拟稳态生产阶段,低导流能力裂缝的产量分布趋于均匀,高导流能力裂缝的产量分布进一步非均匀。
参考文献:
[1] PENMATCHA V R. Modeling of horizontal wells with pressure drop in the well[D]. Palo Alto: Stanford University. Petroleum Reservoir Institution, 1997: 156-164.
[2] 姚军, 李爱芬. 单孔隙介质渗流问题的统一解[J]. 水动力学研究与进展: A辑, 1999, 14(3): 317-324.
YAO Jun, LI Aifen. General solutions for seepage flow in single porous medium[J]. Journal of Hydrodynamics (Ser A), 1999, 14(3): 317-324.
[3] GRINGARTEN A C, RAMEY JR H J. The use of source and Green's functions in solving unsteady flow problems in reservoirs[J]. Society of Petroleum Engineers Journal, 1973, 13(5): 285-296.
[4] 宁正福, 韩树刚, 程林松, 等. 低渗透油气藏压裂水平井产能计算方法[J]. 石油学报, 2002, 23(2): 68-71.
NING Zhengfu, HAN Shugang, CHENG Linsong, et al. Productivity calculation method of fractured horizontal wells in low permeability oil or gas field[J]. Acta Petrolei Sinica, 2002, 23(2): 68-71.
[5] ZERZAR A, BETTAM Y. Interpretation of multiple hydraulically fractured horizontal wells in closed systems[C]//Canadian International Petroleum Conference. Calgary, Alberta, 2003.
[6] CVETKOVIC B, HALVORSEN G, et al. Modeling the productivity of a multi-fractured horizontal well[C]//SPE Rocky Mountain Petroleum Technology Conference. Keystone, Colorado, 2001.
[7] 曾凡辉, 郭建春, 徐严波, 等. 影响压裂水平井产能的因素分析[J]. 石油勘探与开发, 2007, 34(4): 474-477.
ZENG Fanhui, GUO Jianchun, XU Yanbo, et al. Factors affecting production capacity of fractured horizontal wells[J]. Petroleum Exploration and Development, 2007, 34(4): 474-477.
[8] 徐严波, 齐桃, 杨凤波, 等. 压裂后水平井产能预测新模型[J]. 石油学报, 2006, 27(1): 89-96.
XU Yanbo, QI Tao, YANG Fengbo, et al. New model for productivity test of horizontal well after hydraulic fracturing[J]. Acta Petrolei Sinica, 2006, 27(1): 89-96.
[9] 李军诗, 侯建锋, 胡永乐, 等. 压裂水平井不稳定渗流分析[J]. 石油勘探与开发, 2008, 35(1): 92-96.
LI Junshi, HOU Jianfeng, HU Yongle, et al. Performance analysis of unsteady porous flow in fractured horizontal wells[J]. Petroleum Exploration and Development, 2008, 35(1): 92-96.
[10] 姚同玉, 朱维耀, 李继山, 等. 压裂气藏裂缝扩展和裂缝干扰对水平井产能影响[J]. 中南大学学报(自然科学版), 2013, 44(4): 1487-1472.
YAO Tongyu, ZHU Weiyao, LI Jishan, et al. Fracture mutual interference and fracture propagation roles in production of horizontal gas wells in fractured reservoir[J]. Journal of Central South University (Science and Technology), 2013, 44(4): 1487-1472.
[11] 孙海, 姚军, 廉培庆, 等. 考虑基岩向井筒供液的压裂水平井非稳态模型[J]. 石油学报, 2012, 33(1): 117-122.
SUN Hai, YAO Jun, LIAN Peiqing, et al. A transient reservoir/wellbore coupling model for fractured horizontal wells with consideration of fluid inflow from base rocks into wellbores[J]. Acta Petrolei Sinica, 2012, 33(1): 117-122.
[12] 郝明强, 胡永乐, 李凡华. 特低渗透油藏压裂水平井产量递减规律[J]. 石油学报, 2012, 33(2): 269-273.
HAO Mingqiang, HU Yongle, LI Fanhua. Production decline laws of fractured horizontal wells in ultra-low permeability reservoirs[J]. Acta Petrolei Sinica, 2012, 33(2): 269-273.
[13] 王志平, 朱维耀, 岳明, 等. 低、特低渗透油藏压裂水平井产能计算方法[J]. 北京科技大学学报, 2012, 34(7): 750-754.
WANG Zhiping, ZHU Weiyao, YUE Ming, et al. A method to predict the production of fractured horizontal wells in low/ultralow permeability reservoirs[J]. Journal of University of Science and Technology Beijing, 2012, 34(7): 750-754.
[14] PRATS M. Effect of vertical fractures on reservoir behavior-incompressible fluid case[J]. Society of Petroleum Engineers Journal, 1961, 1(2): 105-118.
[15] MUKHERJEE H, ECONOMIDES M J. A parametric comparison of horizontal and vertical well performance[J]. SPE Formation Evaluation, 1991, 6(2): 209-216.
[16] 李军诗. 压裂水平井动态分析研究[D]. 北京: 中国地质大学石油工程学院, 2005: 1-30.
LI Junshi. A study of performance analysis of horizontal wells with a single or multiple fractures[M]. Beijing: China University of Geosciences (Beijing). Institute of Petroleum Engineering, 2005: 1-30.
[17] 李晓平. 地下油气渗流力学[M]. 北京: 石油工业出版社, 2008: 65-75.
LI Xiaoping. Underground oil and gas seepage mechanics[M]. Beijing: Petroleum Industry Press, 2008: 65-75.
[18] 汪志明, 齐振林, 魏建光, 等. 裂缝参数对压裂水平井入流动态的影响[J]. 中国石油大学学报(自然科学版), 2010, 34(1): 73-78.
WANG Zhiming, QI Zhenlin, WEI Jianguang, et al. Interpretation of the coupling model between fracture variable mass flow and reservoir flow for fractured horizontal wells[J]. Journal of China University of Petroleum (Edition of Natural Science, 2010, 34(1): 73-78.
(编辑 陈灿华)
收稿日期:2015-04-10;修回日期:2015-06-22
基金项目(Foundation item):中央财政支持地方高校发展专项资金资助项目(20150727);国家自然科学基金资助项目(51525402, 51504203)(Project (20150727) supported by the Central Government Finance for the Development of Special Funds for Local Colleges; Projects (51525402, 51504203) supported by the National Natural Science Foundation of China)
通信作者:曾凡辉,博士研究生,讲师,从事油气藏开采研究;E-mail:zengfanhui023024@126.com