等温局部加载成形过程中坯料变厚区过渡条件演化
来源期刊:中国有色金属学报(英文版)2014年第4期
论文作者:张大伟 杨 合
文章页码:1101 - 1108
关键词:筋板类构件;等温局部加载;不等厚坯料;坯料变厚区;倒角过渡形式;钛合金
Key words:rib-web component; isothermal local loading; unequal-thickness billet; variable-thickness region of billet; beveling transition pattern; titanium alloy
摘 要:采用简单不等厚坯料结合等温局部加载方法,低成本有效地控制大型钛合金筋板类构件成形过程中的材料流动和改善型腔充填。由于倒角过渡形式结构简单、过渡条件范围宽,因此坯料变厚区采用倒角过渡形式较好。局部加载成形过程中的过渡条件演化对坯料变厚区未约束部分的动态边界条件有显著影响。基于合理的假设,应用理论分析建立过渡条件演化模型。应用所建立模型的预测结果与实验和有限元分析结果进行比较,结果表明模型是可靠的。建立的过渡条件演化模型能够很好地处理变厚区未约束部分的动态边界,适用于对多筋构件局部加载成形中材料流动和型腔充填的快速分析。
Abstract: Using simple unequal-thickness billet combining isothermal local loading can control the metal flow and improve the cavity fill in manufacturing process of large-scale rib-web titanium alloy component with low cost and short cycle. The beveling transition pattern is well used for variable-thickness region of billet (VTRB) due to its simple and ample range of transition condition. The transition condition development in the local loading process has a significant influence on dynamic boundary of unrestricted portion of VTRB. With the help of reasonable assumptions, a mathematical model of transition condition development was established by theoretical analysis. The predicted results for local loading process of rib-web component using the established model were compared with the numerical and experimental ones, and the results indicated that the model of transition condition development is reasonable. Using the established model could deal with the dynamic boundary of unrestricted portion of VTRB well, and the model is suitable for the analysis of metal flow and cavity fill in local loading process of multi-ribs component.
Trans. Nonferrous Met. Soc. China 24(2014) 1101-1108
Da-wei ZHANG1,2, He YANG2
1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;
2. School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China
Received 24 April 2013; accepted 9 August 2013
Abstract: Using simple unequal-thickness billet combining isothermal local loading can control the metal flow and improve the cavity fill in manufacturing process of large-scale rib-web titanium alloy component with low cost and short cycle. The beveling transition pattern is well used for variable-thickness region of billet (VTRB) due to its simple and ample range of transition condition. The transition condition development in the local loading process has a significant influence on dynamic boundary of unrestricted portion of VTRB. With the help of reasonable assumptions, a mathematical model of transition condition development was established by theoretical analysis. The predicted results for local loading process of rib-web component using the established model were compared with the numerical and experimental ones, and the results indicated that the model of transition condition development is reasonable. Using the established model could deal with the dynamic boundary of unrestricted portion of VTRB well, and the model is suitable for the analysis of metal flow and cavity fill in local loading process of multi-ribs component.
Key words: rib-web component; isothermal local loading; unequal-thickness billet; variable-thickness region of billet; beveling transition pattern; titanium alloy
1 Introduction
Isothermal local loading method integrating the advantages of local loading and isothermal forging has been used to manufacture large-scale complex component made by hard-to-deform alloy such as titanium alloy and aluminum alloy [1-3]. The local loading method realized by dividing the upper or lower die into several parts is a simple and efficient way for large-scale rib-web component [3,4]. Using proper unequal-thickness billet (thickness of billet is changed using simple structure) combining local loading can control the metal flow and improve the cavity fill in manufacturing process of large-scale rib-web titanium alloy component with low cost and short cycle.
Common practice in the preform design is to consider planes of metal flow, i.e. selected cross sections of the component [5-7]. Thus, it is necessary to fast analyze metal flow and cavity fill on the cross section. For isothermal local loading process of large-scale rib-web component, the numerical simulation provides mass data and it is difficult to master basic forming law quickly, and then analysis and optimization for each metal-flow plane need numerous workloads. Conversely, the analytical model has a clear physical insight, and its computation is simple and efficient. The isothermal local loading process of large-scale complex-structure titanium alloy component is an isothermal forming process under elevated temperature and low loading speed. At these forming conditions, the assumption and simplification of slab method (SM) approach the true process conditions [8].
ZHANG and YANG [9] presented that the local loading states in local loading process of rib-web component were determined by geometric parameters of die (GPD) and geometric parameters of billet (GPB), respectively, and two loading processes of T-shaped component were designed which could reflect the local loading characteristic under different local loading states, as shown in Fig. 1. Using the SM, the analytical models have been established to describe the metal flow of the two T-shape components under local loading [9,10], and the metal flow on the plane can be fast analyzed by the model.

Fig. 1 Sketch of local loading processes of multi-ribs and T-shaped components
In local loading state caused by GPB, the constrained end of variable-thickness region of billet (VTRB) affected the development of geometric parameters in VTRB, and metal flow was determined by these geometric parameters, such as dynamic width of local loading, thickness of billet and transition condition of VTRB for certain material and component. The distance (L) between the center of rib cavity and the vertical wall of lower die was a parameter to describe the constrained end in Ref. [9], and the L was a constant in the SM model. However, in local loading process of multi-ribs component, the constrained boundary was dynamically changing. In order to solve the problem of dynamic constrained boundary, the process can be discretilzed into many intervals, and the SM model in the Ref. [9] was used in an interval, and then the position of constrained end and parameters L were updated in each interval. This needed to consecutively update the parameters in VTRB including the transition condition of VTRB. However, the development of transition condition was not considered in the previous study, where only the initial transition condition was considered. Thus, it urgently needs to explore the development of transition condition for VTRB in the local loading process.
The transition patterns used for VTRB should make the billet simple and be manufactured easily, and should have a flexibility adjustment. The beveling transition pattern met the above requirements due to its simple and ample range of transition condition. The beveling pattern was also adopted for the VTRB in the industrial process of a large-scale titanium alloy bulkhead [11]. Thus, only the beveling transition pattern was investigated in the present study. Based on analysis of deformation characteristic of VTRB, some reasonable assumptions about geometry development of VTRB were proposed, and then the model of transition condition development was established by theoretical analysis. The model was used to predict rib height combining with the previous SM model, and the predicted results showed a good agreement between the results obtained by experiment and finite element method (FEM). The established model was used to deal with the dynamic constrained end, and then metal flow and cavity fill in local loading process of multi-ribs component could be analyzed by analytical methods such as SM.
2 Transition condition and deformation characteristics in VTRB
The research on deformation behavior of VTRB indicates that [12]: the folding/lap is prone to be caused when the VTRB is set near rib cavity and die partitioning boundary, and setting VTRB at web position is a better choice to reduce or eliminate the possibility of folding. Thus, in order to simplify analysis, the forming process of T-shaped component shown in Fig. 1(b) is designed. The transition condition under beveling transition pattern is determined as follows:
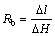 (1)
(1)
where △H is the thickness difference of VTRB; △l is the length of beveling.
Using physical modeling experiment combining slab method, ZHANG et al [10] found that the billet can be divided into several deformation zones according to metal flow, and the deformation zones in the forming process of T-shaped component are shown in Fig. 2(a). O’CONNELL et al [13] presented that the metal flow was restricted by the die wall in closed-die upsetting process and proposed a modification to the traditional SM to reduce deformation zone when applying SM to analyze closed-die upsetting. In the forming process of T-shaped component shown in Fig. 1(b), there also exists similar situation, and then the billet/workpiece can be divided into two distinct layers (Layers 1 and 2) of similar deformation characteristic, as shown in Fig. 2(b). Layer 1 can also be divided into several deformation zones according to metal flow. Figure 2(b) illustrates the deformation zones in Layer 1 which are similar to the deformation zones, as shown in Fig. 2(a).

Fig. 2 Forming process of T-shaped component describing local loading state caused by GPD (a) and GPB (b)
A SM model included the fillet radius (r) between a rib and web was developed by ZHANG et al [14]. The results indicated that there were a few influences when the ratio of fillet radius to rib width (r/b) was greater than 0.75, and the discrepancy between the model in Ref. [10] and the model in Ref. [14] was generally less than 10% when the ratio was 0.25 to 0.75. But the CPU time consumed in Ref. [14] was three times as much as that in Ref. [10], and the model in Ref. [14] was also more complex than the model in Ref. [10]. Thus, the analytical model excluding fillet radius can be used to determine the initial forming parameters at the first optimization stage for large-scale rib-web components local loading. The position of neutral layer shown in Fig. 2(b) can be expressed by SM as follows [9]:
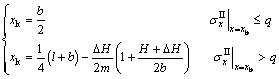 (2)
(2)
where
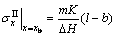 (3)
(3)
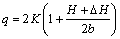 (4)
(4)
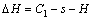 ,
, 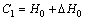 (5)
(5)
where b is the rib width; l is the width of local loading; △H is the thickness difference of VTRB; △H0 is the initial value; H is the thickness of Layer 2; H0 is the initial value; and m is the shear friction factor.
ZHANG and YANG [9] presented that the dynamic l can be expressed as Eq. (6), and the predicted model Eq. (7) about coefficients b1 and b2 was established by partial least squares regression method.
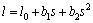 (6)
(6)
 (7)
(7)
Combining volume constancy principle, the thickness of billet in unrestricted portion of VTRB, i.e. the thickness of Layer 2, can be expressed as the differential equations in the process. The differential equation can be solved according to the initial value condition as follows:
 :
:
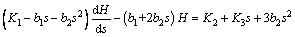 (8)
(8)
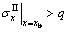 :
:
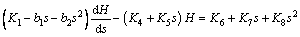 (9)
(9)
where K1-K8 are constants as follows:
 (10)
(10)
 (11)
(11)
 (12)
(12)
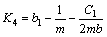 (13)
(13)
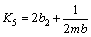 (14)
(14)
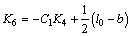 (15)
(15)
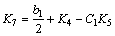 (16)
(16)
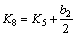 (17)
(17)
3 Modeling for transition condition development in local loading process
The distance L between center of rib cavity and the constrained end of Layer 2 is an important parameter in Eqs. (7)-(9), but the L is a constant in Ref. [9]. In fact, the constrained end often is the adjacent VTRB in multi-ribs component local loading process, as shown in Fig. 3, and thus, the constrained end is dynamically changing and then the parameter L is also dynamically changing.
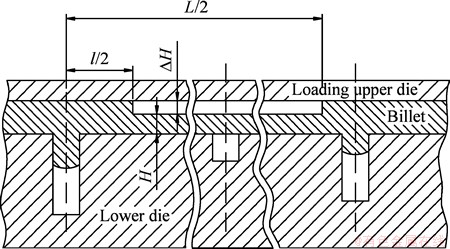
Fig. 3 Restrained end of Layer 2 in multi-ribs component local loading process
In order to solve the problem caused by dynamic constrained end, the process is discretized into many intervals, and the model in Ref. [9] can be used in an interval. The position of constrained end and parameters L are updated after calculating in the interval, and the l, H and △H are also updated according to Eqs. (5)-(9). The updated parameters will be used as initial parameters in the next interval. The transition condition Rb is one of predictor variables in Eq. (7), however, it appears that the updated result on the transition condition can not be obtained according to the previous study. The SM analysis of multi-ribs component local loading process can be running smoothly only with consecutive updated Rb. Thus, it urgently needs to investigate the development of transition condition in the local loading process.
Considering the deformation characteristics of VTRB, the following assumptions are made for the research and model of the development of transition condition: 1) the warping or haunch-up in the not contacted area (the area between VTRB and vertical wall of lower die, as shown in Fig. 2(b)) is neglected; 2) the thickening of Layer 2 is homogenous; 3) the free surface AB of Layer 1 is a line, as shown in Fig. 4.
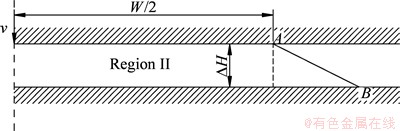
Fig. 4 Simplification of region II
The region II in Layer 1 can be simplified, as shown in Fig. 4. In general, W/△H is much greater than 3.64, and thus the process is a thin-stock compression process, where W=l-2xk.
The process of thin-stock compression has been analyzed by slip-line field method in Refs. [15,16], and the results indicated that the free surface had a uniform flow speed in horizontal direction. If the AB moves in horizontal direction at the same speed, then position of AB is 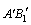 , as shown in Fig. 5, after time increment dt (i.e. after stroke increment ds), and the transition condition Rb is not changed in this case. However, the Layer 2 is thickened by dH after dt in the process, as shown in Fig. 2(b), and it means that the point B moves up by dH in dt. Then, the free surface AB has a velocity vx in horizontal direction and has a velocity vy in vertical direction. The vx is a constant, but the vy is not a constant. The speeds at points A and B can be expressed as follows:
, as shown in Fig. 5, after time increment dt (i.e. after stroke increment ds), and the transition condition Rb is not changed in this case. However, the Layer 2 is thickened by dH after dt in the process, as shown in Fig. 2(b), and it means that the point B moves up by dH in dt. Then, the free surface AB has a velocity vx in horizontal direction and has a velocity vy in vertical direction. The vx is a constant, but the vy is not a constant. The speeds at points A and B can be expressed as follows:
 ,
, 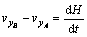 (18)
(18)
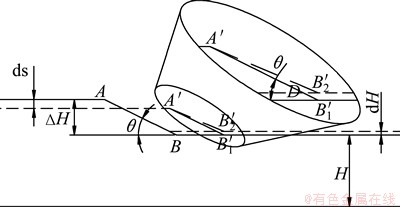
Fig. 5 Deforming sketch of VTRB
In fact, the position of AB is 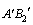 after time increment dt, as shown in Fig. 5, and equation can be obtained according to the definition of transition condition in Eq. (1) as follows:
after time increment dt, as shown in Fig. 5, and equation can be obtained according to the definition of transition condition in Eq. (1) as follows:
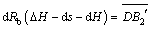 (19)
(19)
The equations can be obtained according to the geometrical relationship shown in Fig. 5 as follows:
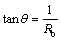 (20)
(20)
 (21)
(21)
Substituting Eqs. (5), (20) and (21) into Eq. (19), and neglecting the second order terms, dRb can be expressed as follows:
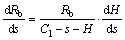 (22)
(22)
Combining the Eq. (22), the modified model considering dynamic L can be obtained. The geometric parameters such as L, l, H, △H and Rb at time t+dt can be determined by Eqs. (5)-(9), and (22) according to the geometric parameters at time t. The position of neutral layer can be calculated by Eq. (2), and then the volume of metal flowing into rib cavity can be calculated, and finally the rib height can be predicted.
4 Results and discussion
4.1 Physical experiment and numerical simulation
In order to simplify the experiment, reduce the cost and save the time, the experiment research is carried out by means of physical modeling of real titanium alloy forming process. DUTTA and RAO [17] found that the lead could be selected as modeling material for titanium alloy hot forming. ZHANG et al [10] declared that the distribution of strain in the local loading process (at room-temperature) using lead was similar to the distribution of strain in the local loading process (at elevated temperature) using Ti-6Al-4V titanium alloy. The forming process, as shown in Fig. 1(b), is carried out on CSS series electronic universal testing machine, and the initial geometric parameters are l0=52, 40 mm; L0=90 mm; H0=8 mm; △H0=4 mm; Rb=2.
Based on plane strain, the finite element model for isothermal forming process of T-shaped component has been developed through DEFORM package, and the model has been verified with respect to rib height and folding defect [9,12]. The von Mises yielding criteria and shear friction model are employed. The local refined meshing and automatic remeshing techniques are used to avoid meshing-induced singularity. Lead and Ti-6Al-4V titanium alloy are used in the numerical simulation. The flow behavior of lead is expressed by [10]
 (23)
(23)
The flow behavior of Ti-6Al-4V titanium alloy comes from the material library of DEFORM. The main forming parameters are listed in Table 1. Through changing geometric models of billet and dies, the finite element model is also suitable for simulating the local loading process of multi-ribs. The shapes of specimen after deformation obtained by FEM and experiment are shown in Fig. 6, and the comparison of rib height in process is shown in Fig. 7. It can be found from FEM results in Fig. 7 that the result using lead is almost identical to the result using Ti-6Al-4V titanium alloy. It further validates that the lead can be selected as modeling material for titanium alloy hot forming.
Table 1 Parameters in analyses by different methods
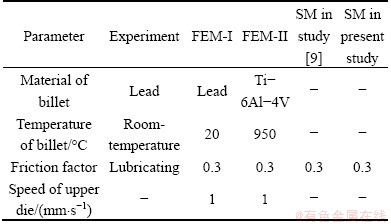

Fig. 6 Shape of billet after deformation (l0=52 mm)
4.2 Verification of model
The development of transition condition was not considered in Ref. [9], where boundary (described by L in the model) of unrestricted portion of VTRB was unchanged. The model of transition condition development is established in Section 3. The SM model coupled with model of transition condition development can be used to analyze the local loading process of multi-ribs component, where the constrained boundary (L) is dynamically changing. For T-shaped component, parameter L is a constant in the process, so the results in the present study should be identical to the results in Ref. [9]. In order to validate the development model of Rb established in Section 3, the comparison of rib height obtained by different method is carried out.
In the SM analysis of process shown in Fig. 1(b), the width of local loading is predicted by Eqs. (6) and (7), and the coefficients b1 and b2 and the constants C1, K1-K8 remained unchanged in Ref. [9]. However, in the present study, the forming process is discretilzed into many intervals. The number of intervals is determined by the stroke. The interval is 0.1 mm in the present study. In each interval, the b1, b2, C1 and K1-K8 are calculated according to the geometric parameters, and the Rb and other geometric parameters are updated in the end of interval.
The rib height at local loading stage in the process shown in Fig. 1(b) had been investigated by means of experiment, FEM, SM in Ref. [9] and the present study. The initial geometric parameters are l0=52, 40 mm, L0=90 mm, H0=8 mm, △H0=4 mm, Rb=2, and the main forming parameters are listed in Table 1. The comparison of rib heights obtained by different methods is shown in Fig. 7.
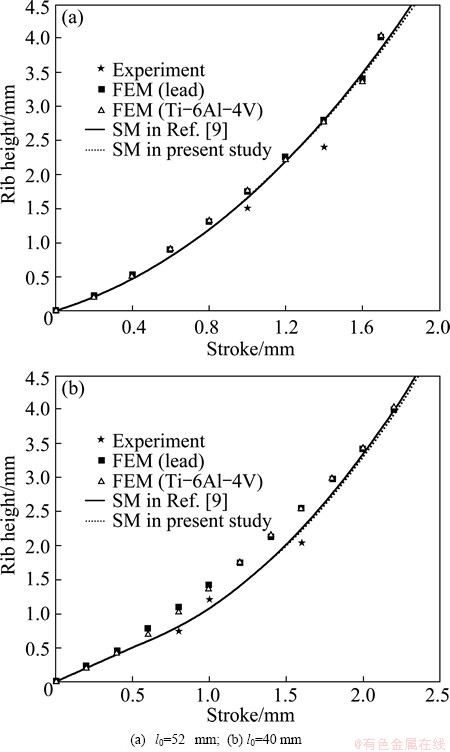
Fig. 7 Rib height by different methods
The comparison in Fig. 7 indicates that the predicted results by SM in the present study are coincident with those in Ref. [9], and shows good agreement with the results by FEM and experiment. The error between SM and experiment is less than about 15%. The geometric parameters for Fig. 7 are symmetrical about the center of rib. For the condition that the geometric parameters are asymmetrical about the center of rib, the center of rib cavity is assumed as symmetry plane for left and right regions, respectively, and then geometric parameters in left or right region can be calculated by Eqs. (5)-(9) and (22), and the neutral layer xk can be calculated by Eq. (2), so the metal flowing into rib cavity in left or right region can be obtained. Then the rib heights predicted according to the total volume flowing into rib cavity are obtained, as shown in Fig. 8.
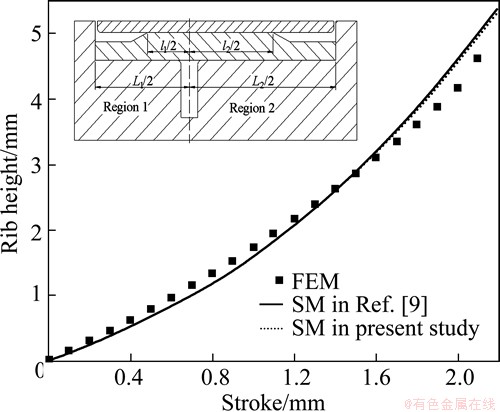
Fig. 8 Rib height under asymmetrical geometric parameters
The initial geometric parameters in both sides are different in Fig. 8: in region 1, l1/b=5 and l1/l1=2.25; in region 2, l2/b=7.5 and l2/l2=2. Other parameters are that: H0/b=1, △H0/H0=0.5, and Rb=2. The finite element analysis (FEA) is also carried out for the process, as shown in Fig. 8, in which Ti-6Al-4V titanium alloy is used, forming temperature is 950 °C, loading speed is 1 mm/s, friction factor is 0.3. It can be seen from Fig. 8 that the predicted result by SM in the present study is coincident with that in Ref. [9], and shows good agreement with the result by FEM. It also indicates that the development model of Rb is reasonable.
4.3 Application of model
Based on development model of Rb established in Section 3, the SM analysis of multi-ribs component local loading process can be carried out, where the L is dynamically changing. All the SM results in this section are obtained by the development model of Rb, i.e. Eq. (22). The local loading process of multi-ribs component, as shown in Fig. 1(a), has two local loading steps, which is presented as following: in the first local loading step, upper die 1 is loaded; in the second local loading step, upper die 2 is loaded. Figure 9 shows the shape of multi-ribs component after two local loading steps.

Fig. 9 Shape of multi-ribs component after two local loading steps
The shape predicted by FEM is the continuous line, and the shape predicted by SM is the dashed line. Where, the Ti-6Al-4V titanium alloy is used in FEA, and the main forming parameters are listed in Table 1. It can be seen from Fig. 9 that the shape of the component predicted by SM agrees well with that predicted by FEM. However, the CPU time consumed by FEM is about 1.60×104 times as much as that consumed by SM. Figure 10 illustrates the comparison of rib height predicted by FEM and SM, whose data are from Fig. 9. There is discrepancy between SM and FEM results, and the relative value for rib 1 is about 15% and that for other rib is less than 10%. The results indicate that the development model of Rb is reasonable.
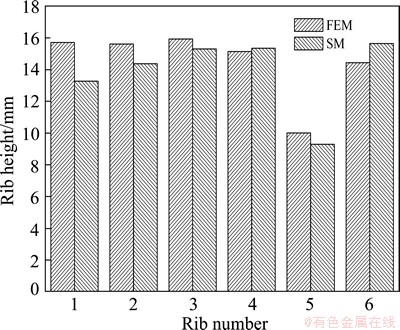
Fig. 10 Rib height of multi-ribs after two local loading steps
The Ti-6Al-4V alloy is a (a+b) titanium alloy, and TA15 (Ti-6Al-2Zr-1Mo-1V) alloy is a near-alpha titanium alloy which is also widely used in China. The conventional forging temperature and near-beta forging temperature are often adopted in the isothermal forming process for these two kinds of titanium alloy, which are 950 °C or above 950 °C. In this range of working temperature, the changes in force parameter are small. For the first local loading step of the local loading process shown in Fig. 1(a), two FEAs are carried out using Ti-6Al-4V titanium alloy (at 950 °C) and TA15 titanium alloy (at 970 °C), respectively, where the flow behavior of TA15 titanium alloy is obtained from Ref. [18]. The other parameters such as loading speed and friction factor are the same, which are 1mm/s and 0.3, respectively. Before the thickness difference △H disappears, the cavity filling behaviors in the isothermal forming process using Ti-6Al-4V titanium alloy are similar that using TA15 titanium alloy, as shown in Fig. 11. It can be found that the errors between SM results and two groups of FEM data are also less than 15%. Thus, the model Eq. (22) can be used to analyze the local loading process of titanium alloy rib-web component.
5 Conclusions
1) Considering the deformation characteristics of VTRB, some assumptions are made for the geometry development of VTRB in isothermal local loading forming process. And then the development model of transition condition under beveling transition pattern is established by theoretical analysis, and its reliability is verified by experiment and finite element simulation.
2) The problem of dynamic constrained end in local loading process of titanium alloy multi-ribs component can be well solved by the development model of transition condition. The result in the present study provides a basis for quickly predicting the metal flow and cavity fill in local loading process of titanium alloy multi-ribs component.
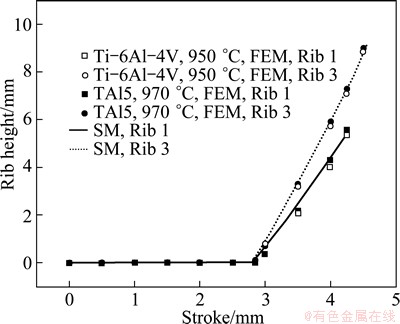
Fig. 11 Rib heights of rib 1 and 3 before △H disappears
Acknowledgment
The first author would like to thank Prof. Sheng-dun Zhao at School of Mechanical Engineering, Xi’an Jiaotong University for helps.
References
[1] YANG H, FAN X G, SUN Z C, GUO L G, ZHAN M. Recent developments in plastic forming technology of titanium alloys [J]. Science China: Technological Sciences, 2011, 54(2): 490-501.
[2] SHAN D B, XU W C, LU Y, SI C H. Research on local loading method for an aluminium-alloy hatch with cross ribs and thin webs [J]. Journal of Materials Processing Technology, 2007, 187-188: 480-485.
[3] SUN Z C, YANG H. Mechanism of unequal deformation during large-scale complex integral component isothermal local loading forming [J]. Steel Research Int, 2008, 79(S1): 601-608.
[4] SARKISIAN J M, PALITSCH J R, ZECCO J J. Stepped, segmented, closed-die forging: United States, 5950481 [P]. 1999.
[5] ALTAN, T, OH S I, GEGEL, H L. Metal forming: Fundamentals and application [M]. Metal, OH: American Society for Metals, 1983.
[6] PARK J J, HWANG H S. Preform design for precision forging of an asymmetric rib-web type component [J]. Journal of Materials Processing Technology, 2007, 187-188: 595-599.
[7] CHOI J C, KIM B M, KIM S W. Computer-aided design of blockers for rib-web type forging [J]. Journal of Materials Processing Technology, 1995, 54: 314-321.
[8]  C R, REBELO N, RYDSTAD H,
C R, REBELO N, RYDSTAD H,  G. Process modelling of metal forming and thermomenchanical treatment [M]. Berlin: Springer-Verlag, 1986.
G. Process modelling of metal forming and thermomenchanical treatment [M]. Berlin: Springer-Verlag, 1986.
[9] ZHANG D W, YANG H. Metal flow characteristics of local loading forming process for rib-web component with unequal-thickness billet [J]. International Journal of Advanced Manufacturing Technology, 2013, 68(9-12): 1949-1965.
[10] ZHANG D W, YANG H, SUN Z C. Analysis of local loading forming for titanium-alloy T-shaped components using slab method [J]. Journal of Materials Processing Technology, 2010, 210: 258-266.
[11] ZHANG D W, YANG H, SUN Z C, FAN X G. A new FE modeling method for isothermal local loading process of large-scale complex titanium alloy components based on DEFORM-3D [C]//NUMIFORM 2010: Proceedings of the 10th International Conference on Numerical Methods in Industrial Forming Processes Dedicated to Professor OC Zienkiewicz (1921-2009). AIP Publishing, 2010, 1252(1): 439-446.
[12] ZHANG D W, YANG H, SUN Z C, FAN X G. Deformation behavior of variable-thickness region of billet in rib-web component isothermal local loading process [J]. International Journal of Advanced Manufacturing Technology, 2012, 63: 1-12.
[13] O’CONNELL M, PAINTER B, MAUL G, ALTAN T. Flashless closed-die upset forging-load estimation for optimal cold header selection [J]. Journal of Materials Processing Technology, 1996, 59: 81-94.
[14] ZHANG D W, YANG H, SUN Z C, FAN X G. Influences of fillet radius and draft angle on the local loading process of titanium alloy T-shaped components [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2693-2074.
[15] SZCZEPINSKI W. Introduction to the mechanics of plastic forming of metals [M]. XU Bing-ye, LIU Xin-sheng, SUN Xue-wei, transl. Beijing: China Machine Press, 1987. (in Chinese)
[16] WANG Zu-tang, GUAN Yan-dong, XIAO Jing-rong, LEI Pei, Huo Wen-can. Theory of metal plastic forming [M]. Beijing: China Machine Press, 1989. (in Chinese)
[17] DUTTA A, RAO A V. Simulation of isothermal forging of compressor disc by combined numerical and physical modeling techniques [J]. Journal of Materials Processing Technology, 1997, 72: 392-395.
[18] SHEN Chang-wu. Research on material constitution models of TA15 and TC11 titanium alloys in hot deformation processes [D]. Xi’an: Northwestern Polytechnical University, 2007. (in Chinese).
张大伟1,2,杨 合2
1. 西安交通大学 机械工程学院,西安 710049;
2. 西北工业大学 材料学院,西安 710072
摘 要:采用简单不等厚坯料结合等温局部加载方法,低成本有效地控制大型钛合金筋板类构件成形过程中的材料流动和改善型腔充填。由于倒角过渡形式结构简单、过渡条件范围宽,因此坯料变厚区采用倒角过渡形式较好。局部加载成形过程中的过渡条件演化对坯料变厚区未约束部分的动态边界条件有显著影响。基于合理的假设,应用理论分析建立过渡条件演化模型。应用所建立模型的预测结果与实验和有限元分析结果进行比较,结果表明模型是可靠的。建立的过渡条件演化模型能够很好地处理变厚区未约束部分的动态边界,适用于对多筋构件局部加载成形中材料流动和型腔充填的快速分析。
关键词:筋板类构件;等温局部加载;不等厚坯料;坯料变厚区;倒角过渡形式;钛合金
(Edited by Chao WANG)
Foundation item: Project (50935007) supported by the National Natural Science Foundation of China; Project (2010CB731701) supported by the National Basic Research Program of China
Corresponding author: He YANG; Tel/Fax: +86-29-88495632; E-mail: yanghe@nwpu.edu.cn
DOI: 10.1016/S1003-6326(14)63168-X

