J. Cent. South Univ. (2017) 24: 382-393
DOI: 10.1007/s11171-017-3440-5

Leader-following coordination of multiple UUVs formation under two independent topologies and time-varying delays
YAN Zhe-ping(严浙平)1, LIU Yi-bo(刘一博)1, YU Chang-bin(于长斌)2, Zhou Jia-jia(周佳加)1
1. College of Automation, Harbin Engineering University, Harbin 150001, China;
2. Research School of Information Science and Engineering, Australian National University, ACT 2614, Australia
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: The new method which uses the consensus algorithm to solve the coordinate control problems of multiple unmanned underwater vehicles (multi-UUVs) formation in the case of leader-following is adapted. As the communication between the UUVs is difficult and it is easy to be interfered under the water, time delay is assumed to be time-varying during the members communicate with each other. Meanwhile, the state feedback linearization method is used to transfer the nonlinear and coupling model of UUV into double-integrator dynamic. With this simplified double-integrator math model, the UUV formation coordinate control is regarded as consensus problem with time-varying communication delays. In addition, the position and velocity topologies are adapted to reduce the data volume in each data packet which is sent between members in formation. With two independent topologies designed, two cases of communication delay which are same and different are considered and the sufficient conditions are proposed and analyzed. The stability of the multi-UUVs formation is proven by using Lyapunov-Razumikhin theorem. Finally, the simulation results are presented to confirm and illustrate the theoretical results.
Key words: multiple unmanned underwater vehicles formation; consensus algorithm; Lyapunov-Razumikhin theory; time-varying delay; state feedback linearization method
1 Introduction
In the past decades, there has been a rapidly growing interest in the development of unmanned underwater vehicles (UUVs) which play important roles in marine exploration and exploitation, such as, deep sea inspections, long-distance, long-duration surveys, and oceanographic mapping to detect, locate and neutralize undersea mines [1, 2]. But sometimes the single UUV hardly accomplishes some complex or high-disk missions with low cost and less sensors, especially in the presence of uncertainties, incomplete information and distributed control. In order to offset the insufficience of single UUV, multi-UUVs formation is used in many ocean missions. Thus, the coordination control of multi-UUVs formation has attracted more attention of control community in recent years. The multi-UUVs formation is defined as a group of UUVs which communicate with each other by underwater acoustic sensors, sometimes even exist communication delays, maintain the formation as redefined configuration and collaborate to achieve a common mission goal and motion state. Comparing with the single UUV, the multi-UUVs formation can provide the mission more increasing efficiency. Meanwhile, it also can be used in more service area, and can guarantee redundancy if one of them is in case of failure.
The main challenges in both single UUV and multi-UUV formation are stable control under the complex marine environment, such as ocean wave, and current [3, 4]. Many literatures have paid lots of attention in single UUV, and the related control methods have been provided and proved, such as, nonlinear control [5], backstepping control [6], sliding and mode control [7, 8] [9, 10]. In one word, the single UUV controlled by these methods can almost accomplish the mission perfectly. But different from single UUV, the multi-UUVs formation should be paid more attention to the collaboration of each member, not just perfect performance of single one. However, the ocean environment increases the difficulty of coordinate control for the whole formation. Some traditional nonlinear control methods, such as, adaptive control, and backstepping control. These methods are used in the multi-UUVs formation control problems [11-13], but most of them are short of the coordination, autonomy and flexibility. To solve these problems, the consensus algorithm which is mostly used in multi-agent system can be adapted in multi-UUVs formation [14-16], especially considering the communication delays or data drop [17-19]. The consensus algorithm is mostly used in multi-agents systems with first or second integral model even in the formation control of unmanned aerial vehicle (UAV) [20-22]. But some provided coordinate control by using consensus algorithm for the multi-UUVs formation may neglect the nonlinear and coupling parameters. Motivated by these literatures and shortages, the accurate model, which can be adapted for the consensus algorithm, and weak communication are the main challenges in the application of combining consensus and coordination control problem of multi- UUVs formation.
The contributions of this work can be described as following aspects. First, different from the previous literatures on consensus algorithm used in the multi-UUVs formation, which usually ignores the nonlinear and coupling parameter in building the math model of single UUV, this work simplifies and linearizes the UUV model with state feedback linearization method by coordinate transformation. Thus, the complex nonlinear model of UUV can be transformed into double-integrator dynamic which can be applied in formation control by consensus algorithm in the following parts. Secondly, different from Ref. [23], the communication topology between the members in formation is divided into position and velocity topologies. The novel communication topologies are applied in the multi-UUVs formation for the first time. In the first case, the communication delays in this novel are assumed as the same. This can be adapted to analyze and prove the stability, convergence and feasibility of this method under the ideal conditions. Thirdly, facing to the real environment conditions, the different delays in this novel topologies are considered, as in the real ocean environment, different topologies mean different communication delays, so the formation is assumed to be operated with two different topologies and communication delays in the second part. Furthermore, the sufficient and necessary conditions of control gains and time delays in this method are provided and proved with Lyapunov- Razumikhin theory.
2 Preliminaries and model description
2.1 Graph theory
A weighted directed graph (digraph) or an undirected graph can be used to represent the information exchanges among the UUVs formation. Let G=(V, ε, A) be a weighted graph consisting of a node set V={1, 2, …, N}, a set of edges  and a weighted adjacency matrix
and a weighted adjacency matrix  which is defined as aij>0, if
which is defined as aij>0, if  while aij=0 otherwise. Moreover, aii=0,
while aij=0 otherwise. Moreover, aii=0, 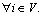 The neighbor set of node is i denoted as
The neighbor set of node is i denoted as  The Laplacian matrix L=[lij] of a weighted graph is defined as
The Laplacian matrix L=[lij] of a weighted graph is defined as
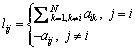
A directed graph G=(V, ε, A) is a sequence of edges in a directed graph of the form (i1, i2), (i2, i3), …,  . A directed graph G=(V, ε, A) is called balanced if and only if all the nodes are balanced.
. A directed graph G=(V, ε, A) is called balanced if and only if all the nodes are balanced.
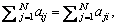
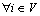
It can be called strongly connected if any two distinct nodes of the graph can be connected by a directed path. In a directed graph G=(V, ε, A), if there is a directed edge from node i to node j, node i is defined as the parent node and node j is defined as the child node. A directed tree is a graph, where every node has exactly one parent except for one node, called the root, which has no parent, and the root has a directed path to every other node. A directed spanning tree of a graph is a directed tree formed by graph edges that connect all the nodes of the graph. A graph has a directed spanning tree if there exists at least one node having a directed path to all the other nodes.
In case of leader-following, another graph 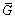 should be concerned associated with the system consisting of n agents and one leader. The leader adjacency matrices can be defined as a diagonal matrix
should be concerned associated with the system consisting of n agents and one leader. The leader adjacency matrices can be defined as a diagonal matrix  with diagonal elements
with diagonal elements  where
where  for some constant ai0>0 if the ith node in G can receive the information from the leader, and otherwise,
for some constant ai0>0 if the ith node in G can receive the information from the leader, and otherwise, 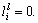
Here are some important properties of Laplacian L [23-25].
Lemma 1: L has at least one zero eigenvalue, and associated eigenvector is 1. All of the nonzero eigenvalues are in the open left half plane. Furthermore, L has exactly one zero eigenvalue and only if the directed graph associated with G has a spanning tree.
Lemma 2: The matrix H=L+B is positive stable if node 0 is globally reachable in 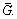
In what follows, Gp and Gv represent the position and velocity interaction topologies respectively. Similarly, Lp, Lv,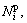
 respectively represent the Laplacian matrices of Gp and Gv and neighbor set of the ith UUV. Moreover,
respectively represent the Laplacian matrices of Gp and Gv and neighbor set of the ith UUV. Moreover, 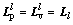 represents the leader adjacency matrices. The adjacency matrices of position and velocity topologies are assumed as the same.
represents the leader adjacency matrices. The adjacency matrices of position and velocity topologies are assumed as the same.
2.2 Feedback linearization of UUV model
The dynamic and model of UUV can be described by 6-DOF model with the body-fixed and earth-fixed coordination as following equations. As the rolling has little influence on the translational motion, the roll speed can be ignored [26].
 (1)
(1)
where  and
and 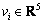 respectively describe the state vectors of velocities and position/Euler angles for the ith UUV. M, C(v) and D(v) denote inertia, Coriolis and damping, respectively, while g(η) is a vector of generalized gravitational and buoyancy forces. The details of J(ηi), M, C(v), D(v) and g(η) are shown in Ref. [22].
respectively describe the state vectors of velocities and position/Euler angles for the ith UUV. M, C(v) and D(v) denote inertia, Coriolis and damping, respectively, while g(η) is a vector of generalized gravitational and buoyancy forces. The details of J(ηi), M, C(v), D(v) and g(η) are shown in Ref. [22].
In this work, the UUV, which is torpedo-like type, is assumed to be symmetrical in plane and vertical, so some parameters can be ignored or simplified. In addition, M and C(v) are symmetric matrix.
In order to change Eq. (1) into the standard nonlinearition function, we should define some matrices firstly.
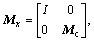

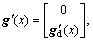
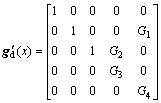
where
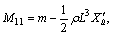
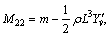
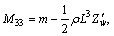
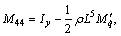
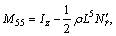
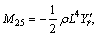
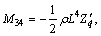
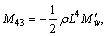
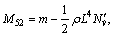
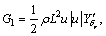
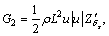
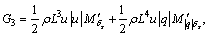
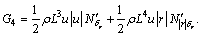
More information on math model and parameters can be obtained from Ref. [22].
Before building standard nonlinearition function, we should obtain f(x), g(x) and h(x) firstly. f(x) and h(x) will be introduced in the following part. g(x) is complex and shown as below:
 (2)
(2)
Then the standard nonlinearition function can be described as
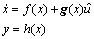 (3)
(3)
As known, the math model of UUV is nonlinear and coupling. We should change the model with state feedback method which is presented below. Before linearization, some theories should be introduced.
Lemma 3: Based on the UUV’s model shown in Eq. (1), the UUV system can be lineared by feedback linearization method, if the following conditions hold:
1) The dimensions of input and output are the same, p=q;
2) The UUV system has relative degree, ρ1, ρ2, …, ρp;
3) The relative degree is the same as the dimensions of the system, ρ=m.
Firstly, for simplifying the processing, the first five elements of f(x) can be assumed as:
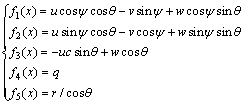 (4)
(4)
The other five elements of f(x) can be ignored as they will not be used in the following. So we define them as fi(x), (i=6, 7, …, 10) for simplifying the calculation.
The output function can be described as
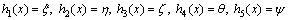
As the outputs we choose are the same as system states in the fixed coordinates. The Lie derivative of hi(x) can be defined as
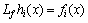 (5)
(5)
and
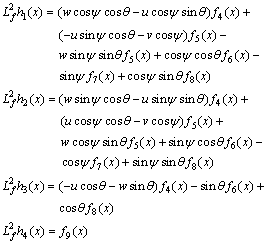
 (6)
(6)
Then
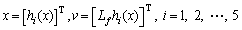 (7)
(7)
 (8)
(8)
where 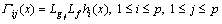
Based on Γ(x) in Eq. (8), we can derive that ρi=2, so
 (9)
(9)
where ρ1,…, ρ5 represent relative degree and m represents the dimensions of the system. According to Lemma 3, the nonlinear math model of UUV can be transformed to linear model by state feedback linearization method.
The new control input, which is used in linearization system, can be defined as
 (10)
(10)
where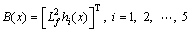 and
and represents the input of nonlinear system in Eq. (3).
represents the input of nonlinear system in Eq. (3).
So the math model of ith UUV in the formation can be modified into standard double-integrator dynamic by feedback linearization method as
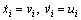 (11)
(11)
where  .
.
Here are some important lemmas for the stability analysis in the subsequent sections [27-29].
Lemma 4: Let ψ1, ψ2 and ψ3 be continuous, nonnegative and non-decreasing function, with ψ1(s)>0, ψ2(s)>0, ψ3(s)>0 for s>0 and ψ1(s)=0, ψ2(s)=0. If there is a continuous function V(t, x) (Lyapunov-Razumikhin function) such that
 (12)
(12)
and there exists a continuous non-decreasing function ψ4(s) with ψ4(s)>s, s>0 such that
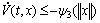 (13)
(13)
When 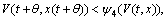
 then origin x=0 is uniformly and asymptotically stable.
then origin x=0 is uniformly and asymptotically stable.
Lemma 5: For a given symmetric matrix S with the form
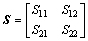 (14)
(14)
where 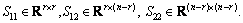 Then, S<0 if and only if S11<0,
Then, S<0 if and only if S11<0, 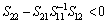 or S22<0,
or S22<0, 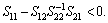
Lemma 6: Assume that 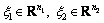 and
and  are defined on the interval Ω. Then, for any matrices
are defined on the interval Ω. Then, for any matrices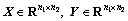 and
and the following holds
the following holds
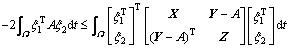
(15)
where 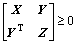
In this work, coordination control problem of multi-UUVs formation is assumed to guarantee all the members to reach a common motion state and desired fixed points related to the formation. This formation can be built with some predesigned distances and angles. In the section above, the math model of UUV has been simplified into double-integrator which is similar to the linear system in the consensus problems. If we neglect the distances and angles, and the leader UUV is regarded as the common point which all the other following UUVs have to catch up with, the coordination control problem of multi-UUVs formation can be seen as the consensus problem of leader-following multi-agents system similarly.
3 Coordination control under independent position and velocity topologies with same time delay
In this section, we assume that the communication topology between members in the formation is divided into position and velocity topologies, and the time delays in two topologies are the same. In this work, we assume that the position and velocity topologies between the leader and followers are the same. Employing the standard double-integrator dynamic of UUV in Eq. (11), the coordination control of multi-UUVs can be designed as follows based on the distributed consensus algorithm.
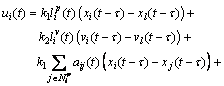
 (16)
(16)
where k1 and k2 represent the gains in position and velocity topologies. τ is the communication delay, aij(t) and bij(t) are respectively the (i, j) entries of the adjacency matrix Ap and Av.  and
and  if the ith UUV can receive the position and velocity information of the leader and
if the ith UUV can receive the position and velocity information of the leader and  and
and  otherwise.
otherwise.
Then the system (11) with the protocol (16) can be summarized as
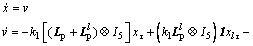
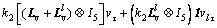 (17)
(17)
where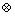 denotes the Kronecker product. xτ, vτ, xlτ and vlτ are short for x(t-τ), v(t-τ), xl(t-τ) and vl(t-τ).
denotes the Kronecker product. xτ, vτ, xlτ and vlτ are short for x(t-τ), v(t-τ), xl(t-τ) and vl(t-τ).  and
and  present the Laplacian matrices of position and velocity topologies with leader. Lp and Lv represent the Laplacian matrices of position and velocity topologies. Simultaneously, we assume that Laplacian matrix of two topologies can be transformed as
present the Laplacian matrices of position and velocity topologies with leader. Lp and Lv represent the Laplacian matrices of position and velocity topologies. Simultaneously, we assume that Laplacian matrix of two topologies can be transformed as
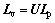 (18)
(18)
where U represents the transformation matrix.
Let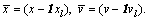 According to Lemma 2, Eq. (17) can be changed with the assumption of
According to Lemma 2, Eq. (17) can be changed with the assumption of 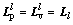 as
as
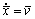
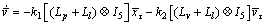 (19)
(19)
Design a new state as 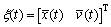
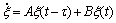
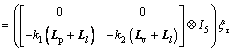
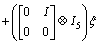 (20)
(20)
where ξ and ξτ are short for ξ(t) and ξ(t-τ).
According to the Leibniz-Newton formula, the time-varying delay of ξτ can be rewritten as
 (21)
(21)
Then, take Eq. (21) into Eq. (20), so Eq. (20) can be changed as
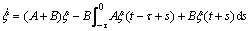 (22)
(22)
For convenience, two new matrices are designed as  and
and 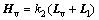 , and we can derive that Hp and Hv are positive stable.
, and we can derive that Hp and Hv are positive stable.
From Lyapunov theorem, as Hp and Hv are positive, then there must be a positive definite matrix Pp and Pv which satisfies 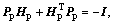
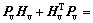
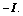
Theorem 1: For case of multi-UUVs system (1) with position and velocity topologies and leader- following formation, the nonlinear model can be linearized, and under the same delays the multi-UUVs system can reach globally stable state if the consensus protocol follows
 (23a)
(23a)
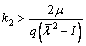 (23b)
(23b)
and with boundary value of delay
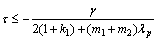 (24)
(24)
where μ is the maximum eigenvalue of Pp; λi is the eigenvalue of M+Pv with  and
and  q>0 which is used for the gain between the position and velocity topologies, and m1>1, m2>1; γ is the minimum eigenvalue of -P(A+B)-(A+B)TP; λp is the maximum eigenvalue of P.
q>0 which is used for the gain between the position and velocity topologies, and m1>1, m2>1; γ is the minimum eigenvalue of -P(A+B)-(A+B)TP; λp is the maximum eigenvalue of P.
Proof: Firstly, to analyze the convergence of system, we define a Lyapunov-Razumikhin function
 (25)
(25)
where  is symmetric and positive definite.
is symmetric and positive definite.
Then the derivative of Eq. (25) can be shown and changed as
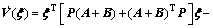
 (26)
(26)
For convenience of calculation, 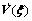 is divided into three parts.
is divided into three parts.
 (27)
(27)
where
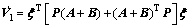
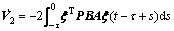
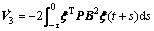
We assumed that 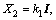
 Z2=P, then
Z2=P, then
 (28)
(28)
By Lemma 6, we can derive
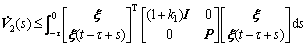
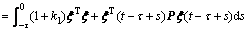
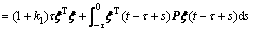
(29)
and similarly, 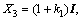
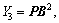
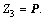
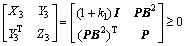 (30)
(30)
So
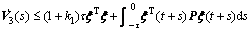 (31)
(31)
Choose ψ4(s)=ms for some constant m>1. According to condition (13) in Lemma 4, it is given:
 (32)
(32)
with m1>1 and m2>1,  and
and can be rewritten as
can be rewritten as
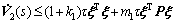 (33)
(33)
 (34)
(34)
So
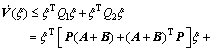
 (35)
(35)
Inequality (35) becomes
 (36)
(36)
with
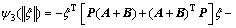
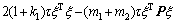
As shown above, 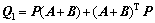 is symmetric matrix, and
is symmetric matrix, and
 (37)
(37)
where  .
.
Then we designed:
 (38)
(38)
so F is positive definite.
According to the Schur complement, we can provide that -Q1 is positive definite if k1 satisfies Eq. (23).
In addition, with the bound of communication delay in Eq. (24), we can derive  for some constant β>0. Equations (32) and (36) satisfy the conditions in Lemma 4. Thus, we can derive that
for some constant β>0. Equations (32) and (36) satisfy the conditions in Lemma 4. Thus, we can derive that  as
as 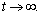
Thus Theorem 1 has been proved.
4 Coordination control under independent position and velocity topologies with different varying time delays
In real multi-UUVs formation, the same delays are difficult to realize. In this section, we assume that the delays in position and velocity topologies are different.
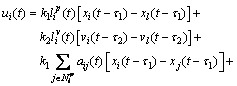
 (39)
(39)
where τ1 and τ2 represent communication delays in position and velocity topologies respectively, aij(t) and bij(t) are respectively the (i, j) entries of the adjacency matrix Ap and Av.
Then system (11) with the protocol (39) can be summarized as
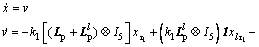
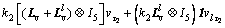 (40)
(40)
where 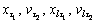 are short for x(t-τ1), v(t-τ2), x1(t-τ1) and v1(t-τ2) respectively.
are short for x(t-τ1), v(t-τ2), x1(t-τ1) and v1(t-τ2) respectively. 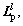
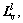
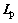 and Lv are the same as the above section. There is also a transformation matrix U between two topologies. In this section, the communication topologies are also assumed as the same,
and Lv are the same as the above section. There is also a transformation matrix U between two topologies. In this section, the communication topologies are also assumed as the same, 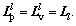
As known above, Eq. (40) can be rewritten as following with 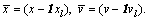
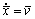
 (41)
(41)
With  Eq. (41) can be changed as
Eq. (41) can be changed as
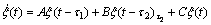
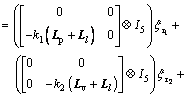
 (42)
(42)
where ξ, and
and  are short for ξ(t), ξ(t-τ1) and ξ(t-τ2) respectively.
are short for ξ(t), ξ(t-τ1) and ξ(t-τ2) respectively.
According to the Leibniz-Newton formula, the time-varying delay of  and
and  can be rewriten as
can be rewriten as
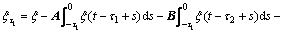
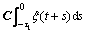 (43)
(43)
and
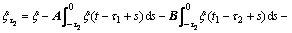
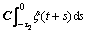 (44)
(44)
With Eqs. (30) and (31), Eq. (29) can be rewritten as

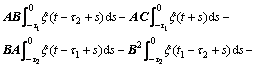
 (45)
(45)
As shown above, we also obtain 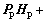
 and
and  with Hp and Hv are positive.
with Hp and Hv are positive.
Theorem 2: For multi-UUVs system (1) with position and velocity topologies, the nonlinear model can be linearized, and under different delays the multi-UUVs system can reach globally stable state if the consensus protocol with
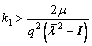 (46a)
(46a)
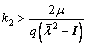 (46b)
(46b)
and with boundary value of delay
 (47a)
(47a)
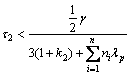 (47b)
(47b)
where μ is the maximum eigenvalue of Pp; λi is the eigenvalue of M+Pv with  and
and  q>0 which is used for the gain between the position and velocity topologies, and mi>1, ni>1; γ is the minimum eigenvalue of -Q1, where
q>0 which is used for the gain between the position and velocity topologies, and mi>1, ni>1; γ is the minimum eigenvalue of -Q1, where 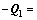
 λp is the maximum eigenvalue of P.
λp is the maximum eigenvalue of P.
Proof: Firstly, the Lyapunov-Razumikhin function can be designed as
 (48)
(48)
where  is symmetric and positive definite.
is symmetric and positive definite.
Calculating 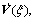 we get
we get
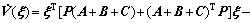
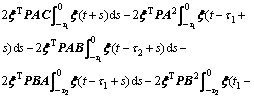
 (49)
(49)
For convenience, dividing  into seven parts:
into seven parts:
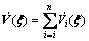
 (50)
(50)
Firstly,
 (51)
(51)
Similar to the above, we assume that  Zi=P, (i=2, 3, …, 7), Y2=PA2, Y3=PAB, Y4=PAB, Y5=PBA, Y6=PB2, Y7=PBC, then we can derive
Zi=P, (i=2, 3, …, 7), Y2=PA2, Y3=PAB, Y4=PAB, Y5=PBA, Y6=PB2, Y7=PBC, then we can derive
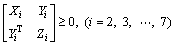 (52)
(52)
which satisfies the condition of Lemma 6.
So  (i≥2) can be changed into follows.
(i≥2) can be changed into follows.
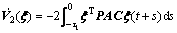
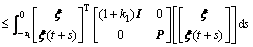
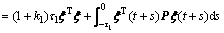
and similarly,

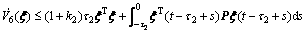
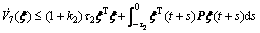
Choose ψ4=ms for some constant m>1. According to condition (13) in Lemma 4.
 (53)
(53)
where 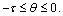
With mi>1, ni>1, (i=1, 2, 3), inequality (49) can be changed into
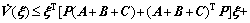
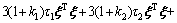
 (54)
(54)
where m=n=3.
Inequality (54) becomes
 (55)
(55)
where
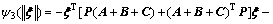
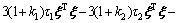
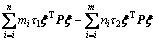
Similar to the section above with the same delays,  is a symmetric matrix, and
is a symmetric matrix, and
 (56)
(56)
where 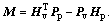
Thus we can provide the -Q1 is positive definite if k 1 and k 2 satisfy (46a) and (46b).
In addition, with the bounds of communication delays in (47a) and (47b),
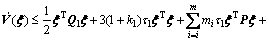
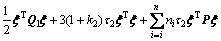 (57)
(57)
We can derive 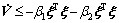 for some constant β1>0, β2>0. Inequalities (53) and (55) satisfy the conditions in Lemma 3. Thus, we can derive that
for some constant β1>0, β2>0. Inequalities (53) and (55) satisfy the conditions in Lemma 3. Thus, we can derive that  as
as 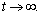
Thus Theorem 2 has been proved.
5 Simulation result
To illustrate the theoretical results obtained in the previous sections, some simulations are given. Figure 1 shows the velocity and position topologies with 5 UUVs (one leader and four followings) in formation. The corresponding adjacency matrices are limited to 0 and 1 matrices. The communication topologies are divided into two parts. The blue topology shows the position topology, and the black one is velocity topology. In addition, we suppose that the initial position and velocity of all UUVs are set randomly. The leader is operated on the desired path. The desired path can be assumed as spiral curve, and it can be expressed as
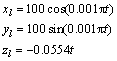
 (58)
(58)
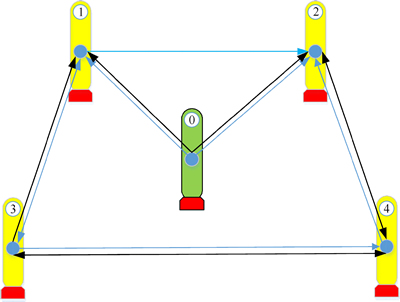
Fig. 1 Position and velocity topologies
The detail parameters of rigid body and nominal hydrodynamic coefficients are shown and described [30]. Associated with Gp and Gv in Fig. 1, the Laplacian matrices can be obtained as

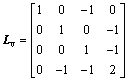
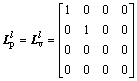
For the case with the same time-varying delay in formation, under the condition in Theorem 1, the same delay is set as τ=0.25[1+sin(2t)] which means that the delays vary between 0 and 0.5. The control parameters are displayed as follows: k1=0.243, k2=0.8757. The simulation results are shown in Figs. 2-4. The position and attitude states of all UUVs in formation are shown in Fig. 2. As shown, all the states can reach the stable point, including the position and velocity state. Figure 3 presents the velocity states of UUVs for 6 DOF achieve the average consensus asymptotically. In Fig. 4, it shows that with the random initial position and velocity, the followers can catch up with the leader and then operated on the desired path.
For the case with different time-varying delay in formation, under the condition in Theorem 2, different delays are set as τ1=0.25[1+sin(2t)], τ2=0.2[1+cos(2t)], which means that τ1 and τ2 vary between 0-0.5 and 0-0.4 respectively. The control parameters are displayed as
follows: k1=0.243, k2=0.8757. The simulation results are shown in Figs. 5-7. The position and attitude states of all UUVs in formation are shown in Fig. 5. As shown, the pitch of all members in formation are stable at 0.175 rad in which case the AUVs dive at expected velocity. Figure 6 shows the velocity states of UUVs achieve the average consensus asymptotically. The translation velocity of following members concurrence to the leader and angular velocities are stable at 0 rad/s and 0.006 rad/s. Comparing with Case 1, it takes more time to adjust the state and position in second case. In Fig. 7, the followers can catch up with the leader and then operate on the
desired path with the random initial position and velocity.
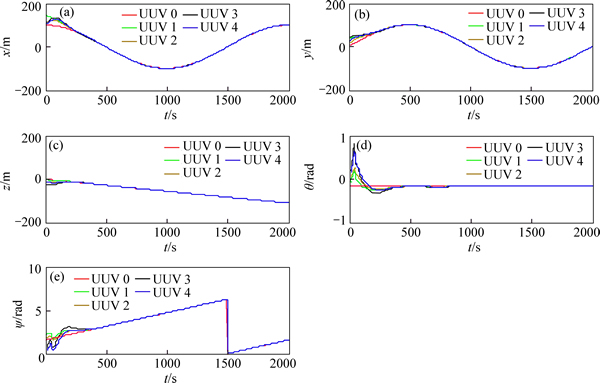
Fig. 2 Position and attitude states of UUVs
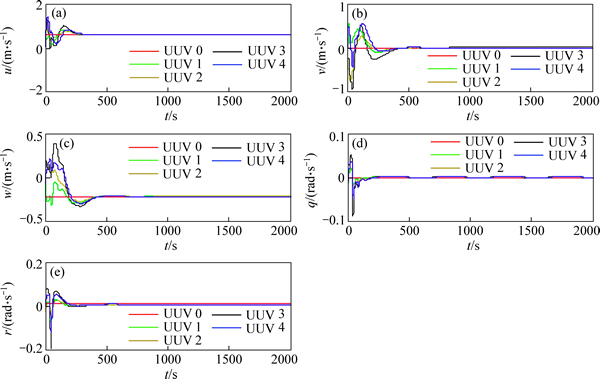
Fig. 3 Velocity states of UUVs
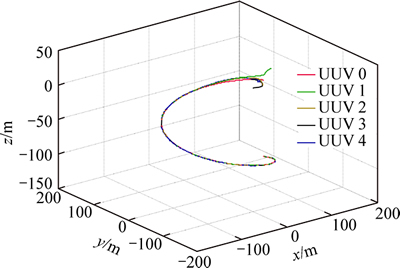
Fig. 4 3D trajectories of all UUVs in formation

Fig. 5 Position and attitude states of UUVs
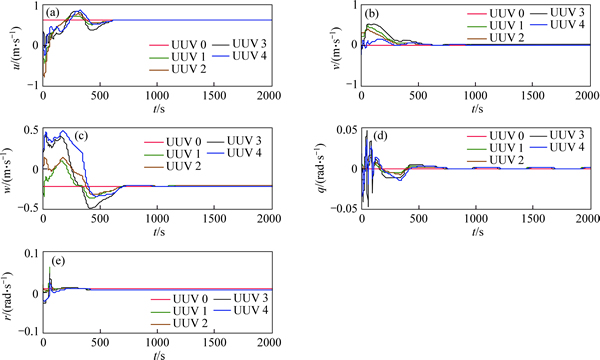
Fig. 6 Velocity states of UUVs
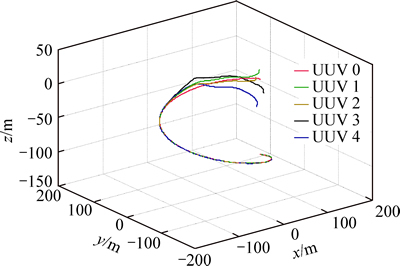
Fig. 7 3D trajectories of all UUVs in formation
6 Conclusions
The multi-UUVs formation control combined with consensus theory under two independent topologies with the same and different communication delays is discussed. By Lyapunov-Razumikhin theory and state feedback linearization method, we have proposed the stability conditions for the multi-UUVs in the case of leader-following. Thus, multi-UUVs formation control problem is regarded as a consensus problem. For these special consensus problems on multi-UUVs, the conditions presented can guarantee the uniformly ultimate stability of the formation. Finally, simulation results have been given to validate the theoretical results. In future works, we would like to discuss and design consensus algorithm for multi-UUVs formation with switching position and velocity topologies in the case of saturation characteristics and also consider the influence of time-varying delays.
References
[1] CHEN Qiang. Unmanned underwater vehicle [M]. Beijing, China: National Defense Industry Press, 2014. (in Chinese)
[2] YUH J. Design and control of autonomous underwater robots: A survey [J]. Autonomous Robots, 2000, 8(1): 7-24.
[3] YAN Zhe-ping, LIU Yi-bo, ZHOU Jia-jia, WU Di. Path following control of an AUV under the current using the SVR-ADRC [J/OL]. Journal of Applied Mathematics, 2014(2014): 1-12.
[4] PENG Zhou-hua, WANG Dan, SHI Yang, WANG Hao, WANG Wei. Containment control of networked autonomous underwater vehicles with model uncertainty and ocean disturbances guided by multiple leaders [J]. Information Sciences, 2015, 316: 163-179.
[5] LAPIERRE L, SOETANTO D. Nonlinear path-following control of an AUV [J]. Ocean engineering, 2007, 34(11): 1734-1744.
[6] ZHU Da-qi, HUA Xun, SUN Bing. A neurodynamics control strategy for real-time tracking control of autonomous underwater vehicles [J]. Journal of Navigation, 2014, 67(1): 113-127.
[7] JIA He-ming, ZHANG Li-jun, BIAN Xin-qian, YAN Zhe-ping, CHENG Xiang-qin, ZHOU Jia-jia. A nonlinear bottom-following controller for underactuated autonomous underwater vehicles [J]. Journal of Central South University, 2012, 19(5): 1240-1248.
[8] ZHU Da-qi, SUN Bing. The bio-inspired model based hybrid sliding-mode tracking control for unmanned underwater vehicles [J]. Engineering Applications of Artificial Intelligence, 2013, 26(10): 2260-2269.
[9] ZHANG Li-jun, QI Xue, PANG Yong-jie. Adaptive output feedback control based on DRFNN for AUV [J]. Ocean Engineering, 2009, 36(9): 716-722.
[10] ZHANG Li-jun, ZHAO Jie-mei, QI Xue, JIA He-ming. NN-adaptive output feedback tracking control for a class of discrete-time non-affine systems with a dynamic compensator [J]. International Journal of Control, 2013, 86(6):1008-1017.
[11] LI Shi-hua, WANG Xiang-yu, ZHANG Li-jun. Finite-time output feedback tracking control for autonomous underwater vehicles [J]. IEEE Journal of Oceanic Engineering, 2015, 40(3): 727-751.
[12] CUI Rong-xin, GE S S, HOW B V E, CHOO Y S. Leader– follower formation control of underactuated autonomous underwater vehicles [J]. Ocean Engineering, 2010, 37(17): 1491-1502.
[13] PENG Zhou-hua, WANG Dan, WANG Hao, WANG Wei. Distributed coordinated tracking of multiple autonomous underwater vehicles [J]. Nonlinear Dynamics, 2014, 78(2): 1261-1276.
[14] LIN Peng, JIA Ying-min. Average consensus in networks of multi-agents with both switching topology and coupling time-delay [J]. Physica A: Statistical Mechanics and its Applications, 2008, 387(1): 303-313.
[15] HU Jiang-ping, LIN Y S. Consensus control for multi-agent systems with double-integrator dynamics and time delays [J]. IET Control Theory & Applications, 2010, 4(1): 109-118.
[16] PENG Zhou-hua, WANG Dan, ZHANG Hong-wei, LIN Ye-jin. Cooperative output feedback adaptive control of uncertain nonlinear multi-agent systems with a dynamic leader [J]. Neurocomputing, 2015, 149: 132-141.
[17] YANG Hui-zhen, WANG Chuan-feng, ZHANG Fu-min. A decoupled controller design approach for formation control of autonomous underwater vehicles with time delays [J]. IET Control Theory & Applications, 2013, 7(15): 1950-1958.
[18] LI Shi-hua, WANG Xiang-yu. Finite-time consensus and collision avoidance control algorithms for multiple AUVs [J]. Automatica, 2013, 49(11): 3359-3367.
[19] HU Zhong-liang, MA Chao, ZHANG Li-xian, AARNE H, TASAWAR H, BASHIR A. Formation control of impulsive networked autonomous underwater vehicles under fixed and switching topologies [J]. Neurocomputing, 2015, 147: 291-298.
[20] OLFATI S R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays [J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533.
[21] REN Wei, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies [J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661.
[22] LIU Kai-en, XIE Guang-ming, WANG Long. Containment control for second-order multi-agent systems with time-varying delays [J]. Systems & Control Letters, 2014, 67: 24-31.
[23] HU Jiang-ping, HONG Yi-guang. Leader-following coordination of multi-agent systems with coupling time delays [J]. Physica A: Statistical Mechanics and Its Applications, 2007, 374(2): 853-863.
[24] FAX J A, MURRAY R M. Information flow and cooperative control of vehicle formations [J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1465-1476.
[25] REN Wei, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies [J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661.
[26] FOSSEN T I. Handbook of marine craft hydrodynamics and motion control [M]. New York: John Wiley & Sons Ltd, 2011.
[27] HALE J K, LUNEL S M V. Introduction to functional differential equations [M]. New York: Springer Science & Business Media, 2013.
[28] MOON Y S, PARK P, KWON W H, LEE Y S. Delay-dependent robust stabilization of uncertain state-delayed systems [J]. International Journal of Control, 2001, 74(14): 1447-1455.
[29] BODY S, GHAOUI L E, FERON E, BALAKRISHNAN V. Linear matrix inequalities in system and control theory [M]. Philadelphia, USA: Society for Industrial and Applied Mathematics, 1994.
[30] YAN Zhe-ping, YU Hao-miao, LI Ben-yin. Bottom-following control for an underactuated unmanned undersea vehicle using integral- terminal sliding mode control [J]. Journal of Central South University, 2015, 22(11): 4193-4204.
(Edited by FANG Jing-hua)
Cite this article as: YAN Zhe-ping, LIU Yi-bo, YU Chang-bin, Zhou Jia-jia. Leader-following coordination of multiple UUVs formation under two independent topologies and time-varying delays [J]. Journal of Central South University, 2017, 24(2): 382-393. DOI: 10.1007/s11171-017-3440-5.
Foundation item: Projects(51309067, 51679057, 51609048) supported by the National Natural Science Foundation of China; Project(JC2016007) supported by the Outstanding Youth Science Foundation of Heilongjiang Province, China; Project(HEUCFX041401) supported by the Fundamental Research Funds for the Central Universities, China
Received date: 2016-01-19; Accepted date: 2016-05-03
Corresponding author: LIU Yi-bo, PhD; Tel: +86-18945115756; E-mail:liuyibo8888@126.com