Safe range analysis of clear distance of twin shallow tunnels based on limit analysis and reliability theory
来源期刊:中南大学学报(英文版)2018年第1期
论文作者:王晅 张标 ZHANG Jia-sheng(张家生) 张佳华 成浩
文章页码:196 - 207
Key words:twin shallow tunnels; limit analysis; nonlinear failure criterion; reliability theory; clear distance
Abstract: A method of analyzing the stability of twin shallow tunnels was presented using both limit analysis with nonlinear failure criterion and reliability theory. In the condition of nonlinear failure criterion, the critical clear distances of twin shallow tunnels were obtained by analyzing the change of surrounding pressure. A reliability model was established based on limit state equation, and the failure probability was solved by virtue of Monte Carlo method. Safety factor and corresponding clear distance of different safety levels were obtained by introducing a target reliability index. The scope of clear distance for different safety levels is described, which can be used as a supplement and improvement to the design codes of tunnels.
Cite this article as: ZHANG Biao, WANG Xuan, ZHANG Jia-sheng, ZHANG Jia-hua, CHENG Hao. Safe range analysis of clear distance of twin shallow tunnels based on limit analysis and reliability theory [J]. Journal of Central South University, 2018, 25(1): 196–207. DOI: https://doi.org/10.1007/s11771-018-3729-4.

J. Cent. South Univ. (2018) 25: 196-207
DOI: https://doi.org/10.1007/s11771-018-3729-4
ZHANG Biao(张标), WANG Xuan(王晅), ZHANG Jia-sheng(张家生),ZHANG Jia-hua(张佳华), CHENG Hao(成浩)
School of Civil Engineering, Central South University, Changsha 410075, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: A method of analyzing the stability of twin shallow tunnels was presented using both limit analysis with nonlinear failure criterion and reliability theory. In the condition of nonlinear failure criterion, the critical clear distances of twin shallow tunnels were obtained by analyzing the change of surrounding pressure. A reliability model was established based on limit state equation, and the failure probability was solved by virtue of Monte Carlo method. Safety factor and corresponding clear distance of different safety levels were obtained by introducing a target reliability index. The scope of clear distance for different safety levels is described, which can be used as a supplement and improvement to the design codes of tunnels.
Key words: twin shallow tunnels; limit analysis; nonlinear failure criterion; reliability theory; clear distance
Cite this article as: ZHANG Biao, WANG Xuan, ZHANG Jia-sheng, ZHANG Jia-hua, CHENG Hao. Safe range analysis of clear distance of twin shallow tunnels based on limit analysis and reliability theory [J]. Journal of Central South University, 2018, 25(1): 196–207. DOI: https://doi.org/10.1007/s11771-018-3729-4.
1 Introduction
Tunnels are playing a more and more important role in modern transportation systems. In the past time, single tunnels were popular in engineering because of their low cost and easy construction. However, they cannot keep pace with the development of railways and roads due to the sharp increase of traffic demand and the lack of land resources. Consequently, twin tunnels are more and more prevailing and gradually replace single tunnels on account of their high performances. Nevertheless, both the design and construction of twin tunnels are more complex compared with single ones because the two lines of a twin tunnel interact with each other, which reduces their stability and failures more likely to happen. In other words, the core problem of the stability of twin tunnels is the interaction between the two lines of twin tunnel. The main factor determining their influence is the clear distance. Therefore, study on the influence between the two lines of a twin tunnel and determining the safe range of clear distance is of great scientific value and practical significance [1–3].
Numerous scholars have researched on this problem. AFIFIPOUR et al [4] constructed a three- dimensional finite element model of a twin tunnel under a shallow foundation and researched the influence of the stress, bending moment and displacement on the two tunnels. DO et al [5] carried out numerical simulation by using finite difference software FLAC3D and revealed the influence between the two tunnels related to the clear distance. HOSSAINI et al [6] studied the relationship between clear distance and ground settlement with respect to soft clay through finite element approach and classified the clear distance according to the effect between the two tunnels. Although the numerical simulation method is able to investigate this problem on three dimensions, the results derived are not accurate enough. YOU et al [7] discussed the influence through the width of mid-partition and obtained overall safety factor and local safety factor. By virtue of limit equilibrium method, YANG et al [8, 9] derived the analytical solution of the surrounding pressure of three shallow tunnels with respect to the conditions of both symmetrical loads and unsymmetrical loads. Then, the influence between the three tunnels is discussed based on the change of surrounding pressure. However, the result obtained from the limit equilibrium method is relatively larger. Based on Tresca material, XIE et al [10] investigated the effect between two lines of a twin shallow tunnel by virtue of limit analysis theory. The results agree well with centrifuge test results. SAHOO et al [11] combined limit analysis with finite element method to study the influence of Tresca materials and Coulomb materials and obtained the ranges of clear distance with regard to different buried depth ratios. ZHANG et al [12] made research on the influence between the tunnels by virtue of limit analysis and discussed the influences of clear distance on the surrounding pressure and the range of failure. However, the researches above did not classify the clear distance according to the influence between the two lines of a twin shallow tunnel and the range of safe clear distance was not obtained, either.
Although Code for Design of Road Tunnel [13] has defined the minimum clear distance of the twin tunnels according to the level of surrounding rock. Its reference values are too conservative. This work derived the surrounding pressures from nonlinear limit analysis and studied the influence between the two lines of a twin tunnel according to the change rules of surrounding pressure. In addition, the clear distance is classified according to the influences between two tunnels. Furthermore, by considering the randomness of soil parameters, the safety range of the clear distance with respect to different levels of safety is obtained from reliability theory. The distribution of safety levels based on target reliability index presented in this work supplements and completes the existing code and may be a reference for the design of twin shallow tunnel in practical engineering.
2 Limit analysis with nonlinear failure criterion
A mass of experiments demonstrated that the failure envelop of soil mass has a nonlinear feature. It means that the relationship between shear and normal stress is nonlinear when failure occurs. Thus, the nonlinear Mohr-Coulomb failure criterion which is more suitable for soil mass can be represented as [14, 15]
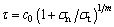 (1)
(1)
where τ and σn are the shear and normal stress on the failure surface, respectively, c0 is the initial cohesion, σt is the axial tensile strength and m is the nonlinear coefficient. Moreover, the values of parameters c0, σt and m can be determined experimentally. It is worth noting that the nonlinear Mohr-Coulomb failure criterion is reduced to linear Mohr-Coulomb failure criterion when the value of m equals 1.
According to the tangent method [16, 17] illustrated in Figure 1, the nonlinear Mohr-Coulomb failure criterion is a curve in the stress space and the tangent passing through a point M on the curve can be obtained
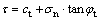 (2)
(2)
in which ct and tanφt are the tangent intercept and the tangent slope, respectively.

Figure 1 Nonlinear failure criterion and tangent method
Then, combining Eq. (1) with Eq. (2), the result is
 (3)
(3)
According to the viewpoint of CHEN [18], the upper bound theorem of limit analysis can be represented as: when the velocity boundary condition is satisfied, the load derived by equating the external rate of work to the rate of energy dissipation in any kinematically admissible velocity field is no less than the actual collapse load. Furthermore, it can be expressed as

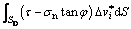 (4)
(4)
where Fi is the load in limit state; 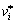 is the velocity vector; S is the length of velocity discontinuity; A is the area of plastic zone; γi is the unit weight of rock mass; σij and
is the velocity vector; S is the length of velocity discontinuity; A is the area of plastic zone; γi is the unit weight of rock mass; σij and 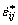 are the stress tensor and strain rate in the kinematically admissible velocity field, respectively.
are the stress tensor and strain rate in the kinematically admissible velocity field, respectively.
The tangent method which introduces nonlinear failure criterion into the upper bound theory of limit analysis can be implemented by substituting Eq. (3) into Eq. (4). On the basis of upper bound theory and the definition of tangent method, an upper bound solution can be obtained.
3 Failure mechanism for twin shallow tunnels
The results of surrounding pressure in existing literatures are mainly based on the failure mechanisms of rock mass for single shallow tunnels. For instance, DAVIS et al [19] suggested that the failure surface of shallow tunnels extents to the ground and constructed four classes of failure mechanisms of purely cohesive soil according to numerous engineering examples. YANG et al [20] proposed two kinds of translational failure mechanisms on the basis of Ref. [19] for frictional- cohesive materials. However, these failure mechanisms are not suitable for twin shallow tunnels. Thus, based on the research of YANG et al [20], the failure mechanism for twin shallow tunnels as illustrated in Figure 2 is constructed in this work. The failure mechanism in Figure 2(a) is bilateral symmetry and only half of the failure mechanism, as the left tunnel drawn in Figure 2(b), needs to be analyzed. The failure mode of left tunnel is consisted of a polygon and 2n triangular rigid blocks.

Figure 2 Collapse mechanism and velocity field of twin shallow tunnels:
Moreover, the left tunnel is divided into the left part and right part in order to consider the influence of the right tunnel on the left one. It is assumed that the right tunnel merely affects the right part of left tunnel and has no impact on the left part. Moreover, the velocity field and surrounding pressure of the left part are regarded as the same with a single shallow tunnel. Therefore, both the velocity field and surrounding pressure are different between the left and right parts of the left tunnel when constructing the failure mechanisms and velocity field. As illustrated in Figure 2(b): H is the buried depth of the tunnel, h denotes the height and length of the tunnel profile, S is the clear distance, v0 is the velocity of rock mass above tunnel and its direction is vertically downward, v1, 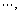 vi,
vi, 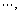 vn are the velocities, v0,1,
vn are the velocities, v0,1, 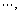 vi–1,i,
vi–1,i, 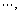 vn–1,n are the relative velocities, β1,
vn–1,n are the relative velocities, β1, 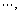 βi,
βi, 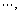 βn and α1,
βn and α1, 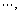 αi,
αi, 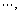 αn are the angular velocities of triangular blocks of left sidewall in order from top to bottom, while
αn are the angular velocities of triangular blocks of left sidewall in order from top to bottom, while 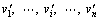 are the velocities,
are the velocities, 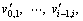
 are the relative velocities,
are the relative velocities, 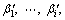
 and
and  are the angular velocities of triangular blocks of right sidewall from top to bottom, φt is the angle between the velocity and discontinuity, q and q′ are the vertical uniform supporting pressures of the left and right arc crown respectively, e and e′ are the horizontal uniform supporting pressures of the left and right sidewall respectively. The vertical supporting pressure and horizontal pressure have the following relationship: e=Kq, e′=Kq′, where K is the coefficient. The velocity fields of left and right parts are illustrated in Figures 2(c) and (d), as well.
are the angular velocities of triangular blocks of right sidewall from top to bottom, φt is the angle between the velocity and discontinuity, q and q′ are the vertical uniform supporting pressures of the left and right arc crown respectively, e and e′ are the horizontal uniform supporting pressures of the left and right sidewall respectively. The vertical supporting pressure and horizontal pressure have the following relationship: e=Kq, e′=Kq′, where K is the coefficient. The velocity fields of left and right parts are illustrated in Figures 2(c) and (d), as well.
4 Calculation process
The following assumptions are made in the computing process: 1) The failure mechanism of tunnels will be considered as a plane problem; 2) The surrounding rock is perfectly plastic and obeys the associated flow rule; 3) The collapsing blocks of the mechanism are rigid and their volume does not change when failure occurs; 4) The right tunnel has only influence on the right part of left tunnel, and its left part can be regarded as part of a single tunnel, i.e., the velocity field and surrounding pressure of left part of left tunnel are the same as a single tunnel.
The surrounding rock pressure of tunnel can be considered as a kind of internal force and the supporting pressure is introduced to calculate the value of surrounding pressure. According to the equilibrium condition of limit state, the supporting pressure applied is equal to the surrounding pressure when tunnel collapses, which can be expressed as: q0=q, q′0=q′. Moreover, only the left tunnel is analyzed due to the symmetry of the twin tunnels.
4.1 Velocity fields
According to the velocity fields illustrated in Figures 2(c) and (d), the velocities of left tunnel can be obtained. Only the expressions corresponding to the left part are presented because the computing processes of left and right part are the same. The velocities of right parts can be obtained by making some little change on the following equations.
 (5)
(5)
 (6)
(6)
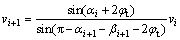
 (7)
(7)

 (8)
(8)
4.2 Work rate of soil weight and internal energy dissipation
4.2.1 Length of discontinuity and area of rigid blocks
The length of discontinuity and the area of rigid blocks with regard to the left part of the left tunnel can be obtained through the following equations.
 (9)
(9)
 (10)
(10)

 (11)
(11)

 (12)
(12)
 (13)
(13)
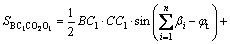
 (14)
(14)

 (15)
(15)
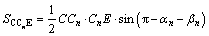 (16)
(16)
The corresponding equations for right part are not presented here due to the calculation process is the same as the left one. The area of the right part rock above the tunnel can be obtained from the following equation
 (17)
(17)
4.2.2 Work rate of soil weight
The work rate provided by the soil weight of the left part can be written as

 (18)
(18)
and that of the right part soil can be expressed as

 (19)
(19)
4.2.3 Work rate of internal energy dissipation
The work rate of internal energy dissipation of the left part corresponding to the left tunnel is
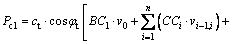
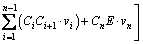 (20)
(20)
and that of the right part is

 (21)
(21)
4.3 Work rate of supporting pressure
The work rate done by supporting pressure corresponding to the left side of the left tunnel is
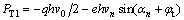 (22)
(22)
and that of the right side is
 (23)
(23)
4.4 Surrounding rock pressure
It is assumed that the surrounding rock pressures on the tunnel in the limit state are generated by the structures in the left and right,respectively. The supporting pressure brought in and the surrounding pressure are balance forces, which means they are opposite in sign but equal in magnitude. Thus, the following equations are found: q=q0, q′=q′0. According to the principle of virtual work and by combining Eqs. (18), (20), (22) with Eqs. (19), (21), (23), the upper bound solutions of the surrounding pressure of the left and right part of the vault can be obtained as
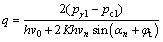 (24)
(24)
 (25)
(25)
Note that the surrounding pressure q is a function of α1, α2, … , αn, β1, β2, … , βn, and q′ is a function of 
 … ,
… , 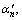
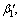
 …,
…,  The geometric constraints of the left and right parts of the velocity fields can be obtained as Eqs. (26) and (27) according to Figures 2(c) and (d). Thus, the problem of finding the maximum values of the surrounding pressures can be transformed to a mathematical model which aims at finding the maximum values of the objective functions q=f(α1, α2, …, αn; β1, β2, …, βn) and q′=
The geometric constraints of the left and right parts of the velocity fields can be obtained as Eqs. (26) and (27) according to Figures 2(c) and (d). Thus, the problem of finding the maximum values of the surrounding pressures can be transformed to a mathematical model which aims at finding the maximum values of the objective functions q=f(α1, α2, …, αn; β1, β2, …, βn) and q′= 
 when the geometric constraints are satisfied. Using sequential quadratic programming method, the maximum values can be derived and they are corresponding upper bound solutions of the surrounding pressure.
when the geometric constraints are satisfied. Using sequential quadratic programming method, the maximum values can be derived and they are corresponding upper bound solutions of the surrounding pressure.
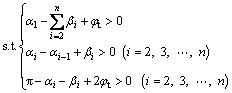 (26)
(26)
 (27)
(27)
4.5 Reliability model
The supporting pressure of the vaults and the side walls can be obtained from the following equations by setting a security coefficient Fs
 (28)
(28)
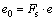 (29)
(29)
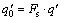 (30)
(30)
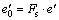 (31)
(31)
Moreover, assuming g1(X), g2(X), g3(X) and g4(X) are the functions with respect to the vault and the side wall of the left and right part of the left tunnel, respectively. The corresponding functions with regard to the right tunnel are g5(X), g6(X), g7(X) and g8(X). Thus, the limit state equations of the twin shallow tunnel can be expressed as
 (32)
(32)
 (33)
(33)
 (34)
(34)
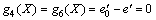 (35)
(35)
The failure of tunnel structure is normally divided into two types based on positions where failure happens, which are the vault and the sidewall. The stability of twin shallow tunnels means both the vault and the side wall are stable. Therefore, the reliability model of the twin shallow tunnels is
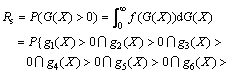
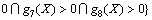 (36)
(36)
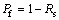 (37)
(37)
 (38)
(38)
where Rs is the degree of the reliability, Pf is the probability of failure, β is the reliability index, X and G(X) are the vectors of random variables and functions respectively. The specific expressions are
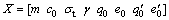 (39)
(39)

 (40)
(40)
5 Analysis of upper bound solutions
The parameters used in the calculation of the upper bound solutions of the surrounding pressures with respect to the twin shallow tunnels are: the buried depth of the tunnel H=20 m, the height and length of the tunnel profile h=10 m, the unit weight of the soil mass γ=20 kN/m3.
5.1 Comparative analysis
Based on the failure mechanism of the single shallow tunnel and the linear failure criterion, YANG et al [20] obtained the upper bound solution of the surrounding pressure. In order to verify the method presented, the parameters in this work are the same with Ref. [20] when calculating the upper bound solutions of surrounding pressure on twin shallow tunnels with different clear distances. These parameters are: nonlinear coefficient m=1.0, cohesion c=10 kPa, angle of internal friction φ=18°, coefficient K which ranges from 0.6 to 1.2, number of the triangular rigid block which is set to 5. The comparison of the upper bound solutions of surrounding pressure is listed in Table 1. It can be seen that: 1) when the value of the coefficient K is 1.2, 1.0, 0.8 and 0.6, the surrounding pressure on the left side of the left tunnel is close to Ref. [20], which validates the correctness of the method put forward in this work; 2) The surrounding pressure on both sides of the tunnel decreases with decreasing K, because the pressure is partially released by the vault. This phenomenon is coincident with Ref. [20]. And the other parts of the pressure causes the increase of influenced scope of surrounding rock and critical clear distance.
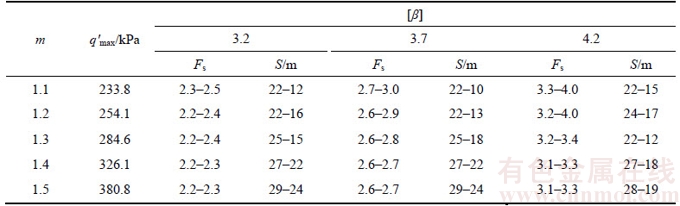
Table 1 Comparison of surrounding pressure from upper bound solutions

5.2 Analysis of clear distance
5.2.1 Linear failure criterion
From Figure 2, it is noted that: when S=–10 m, the two tunnels are overlapped and the twin shallow tunnel can be regarded as a single shallow tunnel, when –10 m

Figure 3 Change rule of collapse pressure on right side of left tunnel based on linear failure criterion
To sum up, twin shallow tunnels can be classified into the following types according to the variation of the surrounding pressures.
1) When S=–h, the two tunnels are overlapped and they can be regarded as a single shallow tunnel;
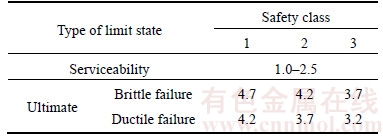
2) When –h 3) When 0 4) When S≥Scr=2.1–2.3h, the interaction between the two tunnels is so small that they can be treated as single shallow tunnels, namely the separated tunnel. Correspondingly, the clear distance can be classified into the following types: 1) According to whether the tunnels interact with each other and regarding S=21–23 m as the critical clear distance of safety, the clear distance is divided as dangerous clear distance and safe clear distance; 2) According to the degree of influence and treating S=5–10 m as the critical clear distance of most dangerous, the clear distance is divided as severely dangerous clear distance and slightly dangerous clear distance. Overall, the clear distance can be divided as severely dangerous clear distance, slightly dangerous clear distance and safe clear distance. 5.2.2 Nonlinear failure criterion Based on nonlinear failure criterion, the change rule of surrounding pressure on the right side of the left tunnel is drawn in Figure 4. The corresponding parameters are: the nonlinear coefficient m=1.1–1.5, initial cohesive c0=10 kPa, axial tensile strength σt=30 kPa, coefficient K=1.0. It can be found that: when S=–10 m, the two tunnels are overlapped and they can be treated as a single tunnel; when –10 m Figure 4 Change rule of collapse pressure on right side of left tunnel based on nonlinear failure criterion (K=1.0) Similar to the change rule of surrounding pressure calculated by linear failure criterion, the surrounding pressure on the right side of the left tunnel under nonlinear failure criterion increases at first, and then it decreases and finally stabilizes. However, the surrounding pressures under the nonlinear failure criterion are larger than that of linear failure criterion. It means introducing the nonlinear feature of the rock mass results in the increase of the surrounding pressure. At the same time, it shows that considering nonlinear characteristic increases the influence between the two tunnels. The results show that when S=9–14 m, the surrounding pressure-clear distance curves reach peak values, which means the right tunnel has most significant influence on the left one. In this case, the tunnels are most unstable and the easiest to collapse. Thus, S=9–14 m can be regarded as the critical clear distance of most dangerous under the nonlinear failure criterion. Besides, when S=22–29 m, the surrounding pressure on the right side of the left tunnel reduces to the minimum and no longer changes, which means the influence between the right tunnel and the left one is negligible. Furthermore, it is found that the minimum surrounding pressure on the right side of the left tunnel is almost the same with that on left side through comparison. Thus, the minimum surrounding pressure on the right side of the left tunnel can be seen as the surrounding pressure on a single shallow tunnel and the corresponding clear distance, S=22–29 m can be treated as critical clear distance of safety. The critical clear distance of nonlinear failure criterion is obviously larger than that of linear failure criterion, which means that the nonlinear property of rock has a large influence on the critical clear distance. As a result, S=9–14 m is regarded as the critical clear distance of most danger and S=22–29 m is treated as the critical clear distance of safety when using nonlinear failure criterion. 6 Reliability analysis 6.1 Sensitivity analysis Assuming that the statistical property of random variables are as listed in Table 2 and other parameters are buried depth H=20 m, height and length of tunnel profile h=10 m, clear distance S= 10 m, coefficient K=1.0 and safety factor Fs=1. The corresponding result of sensitivity analysis is illustrated in Figure 5. It is concluded from Figure 5 that the nonlinear coefficient m is the most sensitive, followed by initial cohesion c0 and unit weight of soil mass γ, while the axial tensile strength σt and the supporting pressures Table 2 Statistical property I of random variables Figure 5 Comparison on sensitivity factors of distribution parameters of random variables 6.2 Safety factor and corresponding clear distance of safety Supposing the statistical properties of random variables are as shown in Table 3 and other parameters are buried depth H=20 m, height and length of the tunnel profile h=10 m and coefficient K=1.0. The failure probability of different safety factors and clear distances under the nonlinear coefficient which is the main factor that affects the reliability derived from Monte Carlo method. According to Code for Design of Railway Tunnel [21], the target reliability index of tunnel structure is listed in Table 4. Moreover, the target reliable index [β], is suggested with respect to the failure probability. Table 5 shows the distribution of safety level, which is illustrated in Figure 6 for the convenience of analysis. Table 3 Statistical property of random variables II Table 4 Target reliability index of tunnel structure According to the example of m=1.2 in Figure 4, the maximum surrounding pressure is obtained as Table 5 Safety factor and corresponding clear distance of different safety ranks for twin shallow tunnels Figure 6 Scope of distribution of safety rank for twin shallow tunnels: 7 Conclusions 1) The failure mechanism of twin shallow tunnels is constructed by extending the failure mechanism of single shallow tunnels, and the upper bound solutions of surrounding pressures are obtained from nonlinear limit analysis. The nonlinear failure criterion reduces to linear failure criterion when the nonlinear coefficient equals 1, and with the same parameters, the solution of surrounding pressure obtained is consistent with previous study which validates the correctness of the method presented. 2) The twin shallow tunnel is classified into the single tunnel, the large-span tunnel, the small spacing tunnel and the separated tunnel according to the change rule of surrounding pressure. Furthermore, the clear distance is divided into severely dangerous clear distance, slightly dangerous clear distance and safe clear distance. The critical clear distance of severely dangerous with respect to the linear and nonlinear failure criterion is S=0.5–1.0h and S=0.9–1.4h, respectively, the corresponding critical clear distance of safety with respect to the two kinds of failure criterion are Scr=2.1–2.3h and Scr=2.2–2.9h, respectively. Considering the nonlinear property of soil mass will increase the critical clear distance. 3) By considering the randomness of soil parameters, it is found that the nonlinear coefficient is the main factor which affects the reliability through sensitive analysis. The failure probability of different safety factors and clear distances with respect to nonlinear coefficient is derived. Besides, the safety factor and corresponding clear distance with respect to different safety levels are obtained by setting a target reliability index. The distribution of safety rank based on target reliability index presented in this work provides a reference for the design of twin shallow tunnels in practical engineering. References [1] MOLLON G, DIAS D, SOUBRA A H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(12): 1363–1388. [2] SENENT S, MOLLON G, JIMENEZ R. Tunnel face stability in heavily fractured rock masses that follow the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60(1): 440–451. [3] OCAK I. A new approach for estimating the transverse surface settlement curve for twin tunnels in shallow and soft soils [J]. Environmental Earth Sciences, 2014, 72(7): 2357–2367. [4] AFIFIPOUR M, SHARIFZADEH M, JAMSHIDI K S A H. Interaction of twin tunnels and shallow foundation at Zand underpass, Shiraz metro, Iran [J]. Tunnelling and Underground Space Technology, 2011, 26(2): 356–363. [5] DO N, DIAS D, ORESTE P, DJERAN-MAIGREA [6] HOSSAINI S M F, SHABAN M, TALEBINEJAD A. Relationship between twin tunnels distance and surface subsidence in soft ground of Tabriz Metro-Iran [C]// 12th Coal Operators' Conference. University of Wollongong & the Australasian Institute of Mining and Metallurgy, 2012: 163–168. [7] YOU K, KIM J. Evaluation of the influence of pillar width on the stability of a twin tunnel [J]. Journal of Korean Tunnelling and Underground Space Association, 2011, 13(2): 115–131. [8] YANG Xiao-li, JIN Qi-yun, MA Jun-qiu. Pressure from surrounding rock of three shallow tunnels with large section and small spacing [J]. Journal of Central South University, 2012, 19(8): 2380–2385. [9] YANG Xiao-li, ZHANG Jia-hua, JIN Qi-yun, MA Jun-qiu. Analytical solution to rock pressure acting on three shallow tunnels subjected to unsymmetrical loads [J]. Journal of Central South University, 2013, 20(2): 528–535. [10] XIE Jun, LIU Chun-gui, YU Hai-yong. Upper bound solutions of plastic limit analysis for the stability of two parallel circular tunnels [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(09): 1835–1841. (in Chinese) [11] SAHOO J P, KUMAR J. Stability of long unsupported twin circular tunnels in soils [J]. Tunnelling and Underground Space Technology, 2013, 38(9): 326–335. [12] ZHANG Jia-hua, XU Jing-shu, ZHANG Biao. Energy analysis of stability of twin shallow tunnels based on nonlinear failure criterion [J]. Journal of Central South University, 2014, 21(12): 4669–4676. [13] JTG D70-2004. Code for Design of Road Tunnel [S]. 2004. [14] YANG X L, ZOU J F. Cavity expansion analysis with non-linear failure criterion [J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering, 2011, 164(1): 41–49. [15] YANG X L. Seismic passive pressures of earth structures by nonlinear optimization [J]. Archive of Applied Mechanics, 2011, 81(9): 1195–1202. [16] HUANG F, YANG X L. Upper bound limit analysis of collapse shape for circular tunnel subjected to pore pressure based on the Hoek-Brown failure criterion [J]. Tunnelling and Underground Space Technology, 2011, 26(5): 614–618. [17] SAADA Z, MAGHOUS S, GARNIER D. Pseudo-static analysis of tunnel face stability using the generalized Hoek-Brown strength criterion [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(18): 3194–3212. [18] CHEN W F. Limit analysis and soil plasticity [M]. Florida: J. Ross Publishing, Inc., 2007. [19] DAVIS E H, GUNN M J, MAIR R J, SENEVIRATINE H N. The stability of shallow tunnels and underground openings in cohesive material [J]. Geotechnique, 1980, 30(4): 397–416. [20] YANG Feng, YANG Jun-sheng. Limit analysis method for determination of earth pressure on shallow tunnel [J]. Engineering Mechanics, 2008, 25(7): 179–184. (in Chinese) [21] TB 10003–2005. Specification for railway tunnel design [S]. 2005. (Edited by FANG Jing-hua) 中文导读 基于极限分析和可靠度理论的双孔浅埋隧道安全净距研究 摘要:本文将非线性破坏准则引入极限分析中,结合极限分析与可靠度理论研究双孔浅埋隧道的稳定性。在围岩服从非线性破坏准则的条件下,通过分析隧道围岩压力得到双孔浅埋隧道的临界净距。在围岩处于极限破坏状态时,构建了隧道的可靠度模型,并运用Monte Carlo法求解了隧道的失效概率。通过引入目标可靠度指标,得到了不同安全等级下隧道的安全系数和相应的安全净距,为今后类似隧道的设计提供了理论依据和参考价值。 关键词:双孔浅埋隧道;极限分析;非线性破坏准则;可靠度理论;净距 Foundation item: Project(51378514) supported by the National Natural Science Foundation of China Received date: 2016-04-18; Accepted date: 2016-07-07 Corresponding author: WANG Xuan, PhD, Lecturer; Tel: +86–18573100781; E-mail: dddebug@csu.edu.cn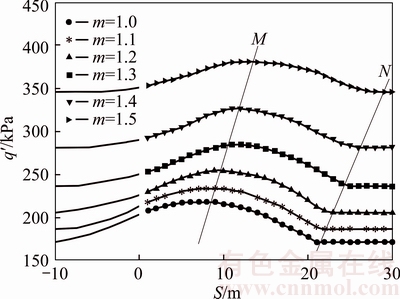

 q0 and e0 are the least sensitive. Thus, the nonlinear coefficient m is the main factor which affects the reliability of twin shallow tunnels.
q0 and e0 are the least sensitive. Thus, the nonlinear coefficient m is the main factor which affects the reliability of twin shallow tunnels.


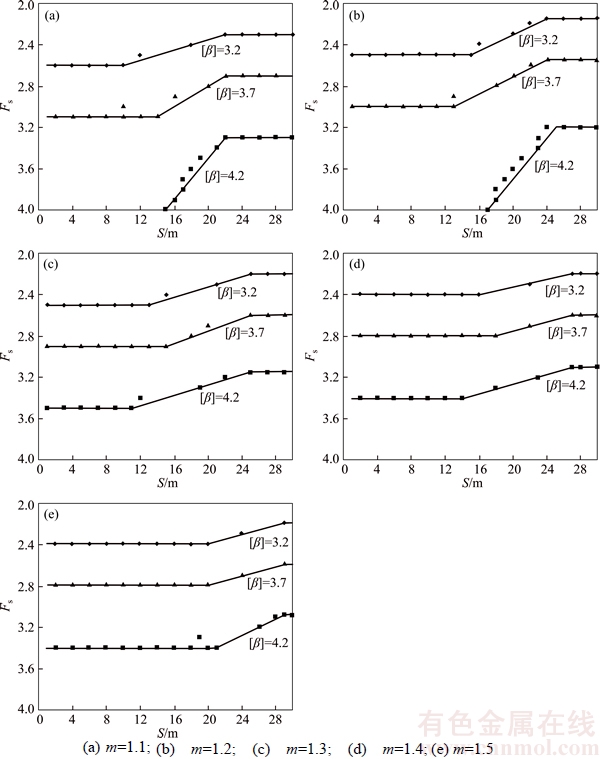
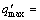 254.1 kPa. By taking this surrounding pressure as a reference value and introducing the safety factor Fs, the reliability model of twin shallow tunnel is constructed to solve the supporting pressure. The results are listed in Table 5 and Figure 6, and the following conclusions are made: 1) The minimum safety factor should be 2.16 corresponding to the 3rd level of safety, namely [β]≥3.2 and the minimum clear distance of safety in this case is 24 m. Furthermore, with the increasing safety factor, the minimum clear distances of safety are 22 m, 20 m, 16 m with a Fs of 2.2, 2.3 and 2.4, respectively. All the clear distances meet the requirement when Fs≥2.5; 2) The minimum safety factor should be 2.55 corresponding to the 2nd level of safety, namely [β]≥3.7 and the minimum clear distance of safety in this circumstance is 24 m. Moreover, with the increasing safety factor, the minimum clear distances of safety are 22 m, 20 m, 18 m and 13 m with Fs of 2.6, 2.7, 2.8 and 2.9, respectively. All of the clear distances meet the requirement when Fs≥3.0; 3) The minimum safety factor should be 3.2 corresponding to the 1st level of safety, namely [β]≥4.2 and the minimum clear distance of safety in this case is 24 m. Moreover, with the increasing safety factor, the minimum clear distances of safety are 23 m, 21 m, 20 m, 19 m, 18 m and 17 m with a Fs of 3.3, 3.5, 3.6, 3.7, 3.8 and 4.0, respectively. It can be seen that the target reliable index and the safety factor increase with the increasing safety level. When the safety levels are the same, the minimum clear distance of safety will decrease with the increasing safety factor. However, the safety factor should not be so small that makes the designed clear distance too large, which may be restricted by terrain conditions and cannot meet the requirement of safety. At the same time, the safety factor cannot be too large from an engineering cost point of view. Thus, the distribution of safety ranks based on target reliability index can be a reference for the design of twin shallow tunnels in the future.
254.1 kPa. By taking this surrounding pressure as a reference value and introducing the safety factor Fs, the reliability model of twin shallow tunnel is constructed to solve the supporting pressure. The results are listed in Table 5 and Figure 6, and the following conclusions are made: 1) The minimum safety factor should be 2.16 corresponding to the 3rd level of safety, namely [β]≥3.2 and the minimum clear distance of safety in this case is 24 m. Furthermore, with the increasing safety factor, the minimum clear distances of safety are 22 m, 20 m, 16 m with a Fs of 2.2, 2.3 and 2.4, respectively. All the clear distances meet the requirement when Fs≥2.5; 2) The minimum safety factor should be 2.55 corresponding to the 2nd level of safety, namely [β]≥3.7 and the minimum clear distance of safety in this circumstance is 24 m. Moreover, with the increasing safety factor, the minimum clear distances of safety are 22 m, 20 m, 18 m and 13 m with Fs of 2.6, 2.7, 2.8 and 2.9, respectively. All of the clear distances meet the requirement when Fs≥3.0; 3) The minimum safety factor should be 3.2 corresponding to the 1st level of safety, namely [β]≥4.2 and the minimum clear distance of safety in this case is 24 m. Moreover, with the increasing safety factor, the minimum clear distances of safety are 23 m, 21 m, 20 m, 19 m, 18 m and 17 m with a Fs of 3.3, 3.5, 3.6, 3.7, 3.8 and 4.0, respectively. It can be seen that the target reliable index and the safety factor increase with the increasing safety level. When the safety levels are the same, the minimum clear distance of safety will decrease with the increasing safety factor. However, the safety factor should not be so small that makes the designed clear distance too large, which may be restricted by terrain conditions and cannot meet the requirement of safety. At the same time, the safety factor cannot be too large from an engineering cost point of view. Thus, the distribution of safety ranks based on target reliability index can be a reference for the design of twin shallow tunnels in the future.