水压力作用下岩石中Ⅰ和Ⅱ型裂纹断裂准则
高赛红1, 2,曹平1,汪胜莲2
(1. 中南大学 资源与安全工程学院,湖南 长沙,410083;
2. 江西理工大学 应用科学学院,江西 赣州,341000)
摘要:为了研究裂隙岩体在水作用下的损伤断裂机制,考虑水产生的垂直裂纹面的静水压力和平行裂纹面的拖拽力,分析处于压剪和拉剪状态的单裂纹应力状态,推导出水作用下裂纹的应力强度因子。还定义基于断裂韧度的损伤变量,并将损伤变量引入Dugdale裂纹模型,推导出水损伤作用下压剪和拉剪应力状态下裂纹的应力强度因子。基于压剪条件下的断裂准则和最大周向应力理论,推导出压剪和拉剪应力状态下,考虑水损伤作用的裂隙岩体断裂准则。
关键词:压剪裂纹;拉剪裂纹;断裂韧度;损伤断裂;断裂准则
中图分类号:TU452 文献标志码:A 文章编号:1672-7207(2012)03-1087-05
Analysis of fracture criterion ofⅠ and Ⅱ type of crack in rock masses under hydraulic pressure
GAO Sai-hong1, 2, CAO Ping1, WANG Sheng-lian2
(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
2. School of Application Sciences, Jiangxi University of Science and Technology, Ganzhou 341000, China)
Abstract: In order to study damage fracture law of fissured rock masses, the hydrostatic pressure vertical to crack surface and drag force parallel to crack surface were taken into consideration, both of which are generated by water action. Stress condition of single crack under compressive-shearing stress condition and tensile-shearing stress condition were calculated respectively. And the stress intensity factor during water action was deduced. A new damage variable related to fracture toughness was presented and the new damage variable was introduced into Dugdale crack model, and the stress intensity factor of compressive-shearing crack and tensile-shearing crack were deduced respectively. Finally, fracture criterion of fractured rock mass considering water damage action was presented, under compressive-shearing stress condition and tensile-shearing stress condition respectively, based on the compressive-shearing fracture criterion and the maximum hoop stress theory.
Key words: compressive-shearing crack; tensile-shearing crack; fracture toughness; damage-fracture; fracture criterion
裂隙岩体有别于其他工程材料,它具有很强的非均匀性、各向异性等力学特征,其在地下水作用下的变形、损伤破坏及稳定性是岩石力学领域关注的课题。水-岩作用包括化学作用和物理作用2个方面。化学作用会使岩石强度弱化,降低岩石的内摩擦角和黏结系数;物理作用即水向裂隙岩体施加动水压力或静水压力,降低结构面上的有效应力,导致微裂纹的扩展和贯通,从而引起岩体力学性质劣化。国内外学者对水作用下岩体断裂损伤问题进行了研究,取得了丰硕的成果[1-15]。朱珍德等[1-3]运用断裂力学和损伤理论推导了含水裂隙岩体的初始开裂强度公式,建立了渗流条件下裂隙岩体的损伤演化方程,并对工程实例进行了分析;汤连生等[4-5]对水-岩作用下岩石的断裂力学效应进行了试验研究,推导出了考虑水压力和水化学损伤作用的岩体断裂强度新准则;丁梧秀等[6]通过不同化学溶液腐蚀岩石的试验,建立了化学腐蚀下裂纹体的断裂准则。本文作者从水-岩物理作用的角度出发,研究水对岩石断裂韧度的影响,进而探讨水对裂纹应力强度因子的影响。
1 水作用下裂纹损伤断裂分析
1.1 压剪应力状态下裂纹的损伤断裂
处于双向受压的含倾斜裂纹岩体的应力状态如图1所示。
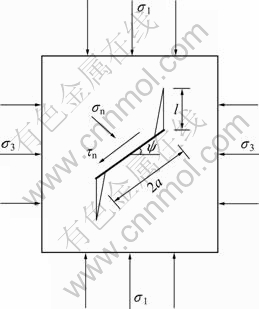
图1 张开型压剪裂纹应力状态
Fig.1 Stress condition of compressive-shearing opening crack
先不考虑渗透压,则裂纹面上的压应力和剪应力分别为(取压为正):
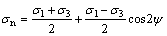 (1)
(1)
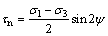 (2)
(2)
式中: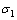 为最大主应力;
为最大主应力;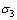 为最小主应力;
为最小主应力;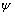 为裂纹倾角。
为裂纹倾角。
根据断裂力学,Ⅰ和Ⅱ型裂纹尖端应力强度因子为[16]:
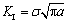 (3)
(3)
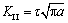 (4)
(4)
式中: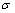 和
和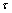 分别为裂纹面上的有效正应力和有效剪应力。
分别为裂纹面上的有效正应力和有效剪应力。
文献[17]指出:裂隙岩体中渗透压力应包括静水压力和动水压力2种,前者对裂隙产生扩张作用,即垂向位移;后者产生拖曳力,使裂隙产生切向位移,此力为面力,并推导出了拖拽力的公式:
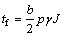 (5)
(5)
式中:b为裂隙宽度;p为充填物的空隙率;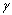 为水的容重;J为水力坡降。
为水的容重;J为水力坡降。
本文引用文献[17]的结果,考虑单一裂隙,提出如下假设:
(1) 裂隙部分张开,张开部分充满水,充填物空隙率为n。
(2) 水流运动规律服从达西定律,裂隙内充填物不随水流运动。
(3) 裂隙承受的水头高度为H。
考虑渗透压作用,则作用在裂隙面上的有效正应力分别为:
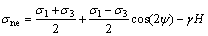 (6)
(6)
在压剪滑动阶段,剪应力使裂纹相对滑动,裂纹接触部分和有充填物部分会产生摩擦力,则作用在裂纹面上的有效剪应力为:
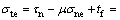
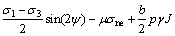 (7)
(7)
式中: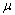 为摩擦因数。则水作用下裂纹尖端Ⅰ和Ⅱ型裂纹强度因子分别为:
为摩擦因数。则水作用下裂纹尖端Ⅰ和Ⅱ型裂纹强度因子分别为:
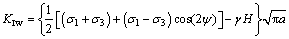 (8)
(8)
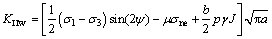 (9)
(9)
当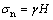 时,裂纹处于临界状态,作用在裂纹面上的水压力与裂纹面上的正应力相等,裂纹面的有效正应力为0,相应的
时,裂纹处于临界状态,作用在裂纹面上的水压力与裂纹面上的正应力相等,裂纹面的有效正应力为0,相应的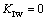 ,裂纹处于稳定状态;当
,裂纹处于稳定状态;当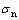 <
<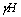 时,
时,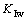 <0;当静水压达到临界水头Hc时,
<0;当静水压达到临界水头Hc时,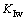 =
=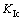 ,裂纹扩展破坏。
,裂纹扩展破坏。
有学者在探讨水作用下岩体的断裂强度时,考虑了损伤作用,认为水对裂纹面剪切强度有影响,具体表现在水对岩体裂纹面的黏聚力c和内摩擦角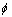 的损伤[5, 14-15],并且定义损伤变量D为:
的损伤[5, 14-15],并且定义损伤变量D为:
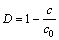 或
或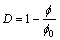 (10)
(10)
式中:c0和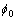 分别为干燥状态下岩体裂纹面上剪切强度指标黏聚力与内摩擦角。本文基于断裂试验结果,定义损伤变量为:
分别为干燥状态下岩体裂纹面上剪切强度指标黏聚力与内摩擦角。本文基于断裂试验结果,定义损伤变量为:
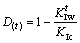 (11)
(11)
其中: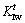 为水作用t时间的断裂韧度;
为水作用t时间的断裂韧度;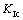 为干燥条件下测得的断裂韧度。
为干燥条件下测得的断裂韧度。
采用双扭试验测试岩石的断裂韧度,计算式如 下[18]:
 (12)
(12)
式中:P为作用于扭杆上的荷载,同时,P与水作用t有关;Wm为扭臂长度;ν为泊松比;d为试件厚度;dn为试件厚度与槽厚之差;W为试件宽度。当P达到临界荷载Pc时,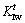 达到临界荷载,即
达到临界荷载,即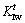 =
=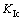 。
。
Dugdale[19]在研究软钢薄板裂纹前缘塑性区所建立的模型是假设在塑性区范围内,塑性屈服的影响相当于增加了裂纹长度。将水损伤引入Dugdale模型[20], 在考虑水对裂纹侵蚀时,主要导致裂纹长度增加和断裂应力减小的情况下,得到水损伤作用下裂纹尖端Ⅰ和Ⅱ型裂纹强度因子分别为:
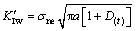 (13)
(13)
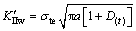 (14)
(14)
测出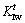 和
和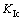 ,结合式(6)~(14)可算出水损伤作用下的应力强度因子。
,结合式(6)~(14)可算出水损伤作用下的应力强度因子。
本文采用周群力[21]提出的压剪断裂准则探讨水压作用下压剪岩石裂纹断裂准则。周群力[21]利用岩石和其他脆性材料进行了压剪断裂试验,提出了以下压剪判据:
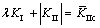 (15)
(15)
式中: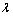 为压剪系数;
为压剪系数;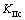 为压缩状态下的剪切韧度。
为压缩状态下的剪切韧度。
根据上文分析结果,可得在渗透压作用下,有充填物的张开型裂纹的断裂准则为:

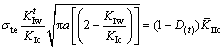 (16)
(16)
1.2 拉剪应力状态下裂纹的损伤断裂
拉剪应力状态下,含单裂纹的岩体如图2所示。
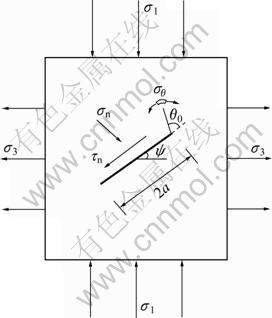
图2 张开型拉剪裂纹应力状态
Fig.2 Stress condition of tensile-shearing opening crack
与压剪裂纹一样,但最小主应力为拉应力,考虑最不利情况,即裂纹张开使得滑动摩擦力消失,则水作用下拉剪应力状态下裂纹面上的有效正压力和剪应力为:
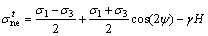 (17)
(17)
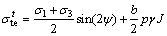 (18)
(18)
分支裂纹的起裂就意味着水损伤演化的开始。大量试验和理论计算表明裂纹起裂是垂直于最大拉应力方向开裂,即按Ⅰ型扩展的。根据最大周向应力理论,裂纹沿最大周向应力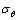 的方向
的方向 扩展,可得拉剪应力状态下分支裂纹起裂时的应力强度因子[22]:
扩展,可得拉剪应力状态下分支裂纹起裂时的应力强度因子[22]:
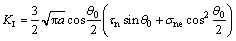 (19)
(19)
引入损伤变量,考虑损伤效应使裂纹长度增加和断裂应力减小,建立水作用下拉剪应力状态下裂纹的断裂准则如下:
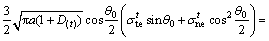
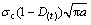 (20)
(20)
式中: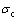 为Ⅰ型裂纹起裂时的极限正应力。
为Ⅰ型裂纹起裂时的极限正应力。
2 结论
(1) 水压力对岩石的作用包括静水力和动水力2个部分。静水力影响裂纹法向有效应力,动水力影响裂纹切向有效应力。考虑单一有充填物的压剪裂纹,其部分张开,将损伤概念引入Dugdale裂纹模型,反映水对裂纹的影响,即导致裂纹长度的增加和断裂应力的减小,定义了新的损伤变量: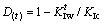 ,推导出了水损伤作用下压剪裂纹的应力强度因子。
,推导出了水损伤作用下压剪裂纹的应力强度因子。
(2) 对处于压剪和拉剪应力状态的含单裂纹岩体,在水作用下的损伤起裂进行了探讨,基于压剪断裂准则和最大周向应力理论,分别给出了考虑水损伤的单裂纹断裂准则。
参考文献:
[1] 朱珍德, 孙钧. 裂隙岩体非稳态渗流场与损伤场耦合分析模型[J]. 山东矿业学院学报: 自然科学版, 1999, 18(3): 50-55.
ZHU Zhen-de, SUN Jun. Coupling model of unstable seepage field and damage field of fractured rock mass[J]. Journal of Shandong Institute of Mining and Technology: Natural Science, 1999, 18(3): 50-55.
[2] 朱珍德, 孙钧. 裂隙岩体的渗流场与损伤场耦合分析模型及其工程应用[J]. 长江科学院院报, 1999, 16(5): 22-27.
ZHU Zhen-de, SUN Jun. Coupling model of seepage field and damage field of fractured rock mass and its application[J]. Journal of Yangtze River Scientific Research Institute, 1999, 16(5): 22-27.
[3] 朱珍德. 地下水对裂隙岩体强度的影响[J]. 山东科技大学学报: 自然科学版, 2000, 19(1): 18-20.
ZHU Zhen-de. The influence of underground water on the strength of fissure rock mass[J]. Journal of Shandong University of Science and Technology: Nature Science, 2000, 19(1): 18-20.
[4] 汤连生, 张鹏程, 王思敬. 水-岩化学作用之岩石断裂力学效应的试验研究[J]. 岩石力学与工程学报, 2002, 21(6): 822-827.
TANG Lian-sheng, ZHANG Peng-cheng, WANG Si-jing. Testing study on effects of chemical action of aqueous solution on crack propagation in rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(6): 822-827.
[5] 汤连生, 张鹏程, 王洋. 水作用下岩体断裂强度探讨[J]. 岩石力学与工程学报, 2004, 23(19): 3337-3341.
TANG Lian-sheng, ZHANG Peng-cheng, WANG Yang. On fracture of rocks with cracks under water action[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3337-3341.
[6] 丁梧秀, 冯夏庭. 化学腐蚀下裂隙岩体的损伤效应及断裂准则研究[J]. 岩土工程学报, 2009, 31(6): 899-904.
DING Wu-xiu, FENG Xia-ting. Damage effect and fracture criterion of rock with multi-preexisting cracks under chemical erosion[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(6): 899-904.
[7] 冯夏庭, 赖户政宏. 化学环境侵蚀下的岩石破裂特性(第一部分): 试验研究[J]. 岩石力学与工程学报, 2000, 19(4): 403-407.
FENG Xia-ting, Ma Sahiro-seto. Rock fracturing behaviors under chemical corrosion (Part Ⅰ): Experimental study[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(4): 403-407.
[8] 王泳嘉, 冯夏庭. 化学环境侵蚀下的岩石破裂特性(第二部分): 时间分形分析[J]. 岩石力学与工程学报, 2000, 19(5): 551-556.
WANG Yong-jia, FENG Xia-ting. Micro-fracturing properties of rock affected by chemical environments (Part Ⅱ): Temporal fractal analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(5): 551-556.
[9] 赵延林, 曹平, 林杭, 等. 渗透压作用下压剪岩石裂纹流变断裂贯通机制及破坏准则探讨[J]. 岩土工程学报, 2008, 30(4): 511-517.
ZHAO Yan-lin, CAO Ping, LIN Hang, et al. Study on fracture mechanism and rheologic fracture failure criterion of compressive-shear rock cracks under saturated pressure[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(4): 511-517.
[10] 赵延林, 曹平, 汪亦显, 等. 裂隙岩体渗流-损伤-断裂耦合模型及其应用[J]. 岩石力学与工程学报, 2008, 27(8): 1634-1643.
ZHAO Yan-lin, CAO Ping, WANG Yi-xian, et al. Coupling Model of seepage-damage-fracture in fractured rock masses and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(8): 1634-1643.
[11] 陈卫忠, 朱维申. 节理岩体断裂损伤耦合的流变模型及其应用[J]. 水利学报, 1999, 30(12): 33-37.
CHEN Wei-zhong, ZHU Wei-shen. Rheology and fracture damage-coupled model for rock mass[J]. Journal of Hydraulic Engineering, 1999, 30(12): 33-37.
[12] 赵延林, 曹平, 文有道, 等. 渗透压作用下压剪岩石裂纹损伤断裂机制[J]. 中南大学学报: 自然科学版 2008, 39(4): 838-844.
ZHAO Yan-lin, CAO Ping, WEN You-dao, et al. Damage fracture failure mechanism of compressive-shear rock cracks under seepage pressure[J]. Journal of Central South University: Science and Technology, 2008, 39(4): 838-844.
[13] 郑少河. 裂隙岩体渗流场–损伤场耦合理论研究及应用[D]. 武汉: 中国科学院武汉岩土力学研究所, 2000: 30-36.
ZHENG Shao-he. Research on coupling theory between seepage and damage of fractured rock mass and its application to engineering[D]. Wuhan: Institute of Rock and Soil Mechanics of Chinese Academy of Sciences, 2000: 30-36.
[14] Dunning J D, Miller M E. Effect of pore fluid chemistry on stable sliding of berea sandstone[J]. Pure and Applied Geophysics, 1984, 122(2/3/4): 447-462.
[15] Rebinder P A, Schreiner L A, Zhigach K F. Hardness reducers in drilling: A physico-chemical method of facilitating the mechanical destruction of rocks during drilling[M]. Moscow: Akad Naunk, Tansl. By Melboune: CSIRO, 1994: 22-27.
[16] 于骁中. 岩石和混凝土断裂力学[M]. 长沙:中南工业大学出版社, 1991: 56-61.
YU Xiao-zhong. Fracture mechanics of rock and concrete[M]. Changsha: Central South University of Technology Press, 1991: 56-61.
[17] 柴军瑞, 仵彦卿. 作用在裂隙中的渗透力分析[J]. 工程地质学报, 2001, 9(1): 29-31.
CHAI Jun-rui, WU Yan-qing. Analysis of seepage action on single-fissure walls[J]. Journal of Engineering Geology, 2001, 9(1): 29-31.
[18] 曹平, 杨慧, 江学良, 等. 水岩作用下岩石亚临界裂纹的扩展规律[J]. 中南大学学报: 自然科学版, 2010, 41(2): 649-654.
CAO Ping, YANG Hui, JIANG Xue-liang, et al. Subcritical crack growth of rock during water-rock interaction[J]. Journal of Central South University: Science and Technology, 2010, 41(2): 649-654.
[19] Dugdale D S. Yielding of steel sheets containing slits[J]. Journal of the Mechanics and Physics of Solids, 1960, 8(2): 100-104.
[20] 汤连生, 王思敬. 岩石水化学损伤的机理及量化方法探讨[J]. 岩石力学与工程学报, 2002, 21(3): 314-319.
TANG Lian-sheng, WANG Si-jing. Analysis on mechanical and quantitative methods of chemical damage in water-rock interaction[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(3): 314-319.
[21] 周群力. 岩石压剪断裂判据及其应用[J]. 岩土工程学报, 1987, 9(3): 33-37.
ZHOU Qun-li, Compress shear fracture criterion of rock and its application[J]. Chinese Journal of Geotechnical Engineering, 1987, 9(3): 33-37.
[22] Ashby M F, Hallam S D. The failure of brittle solids containing small cracks under compressive stress states[J]. Acta Metallurgica, 1986, 34(3): 497-510.
(编辑 陈爱华)
收稿日期:2011-04-24;修回日期:2011-08-17
基金项目:国家自然科学基金资助项目(10972238,51174228)
通信作者:曹平(1959-),男,湖南祁东人,教授,博士生导师,从事岩石断裂力学研究;电话:13973128263;E-mail: pcao_csu@163.com