Active fault-tolerant control scheme of aerial manipulators with actuator faults
来源期刊:中南大学学报(英文版)2021年第3期
论文作者:王尧尧 蒋素荣 丁亚东 陈柏
文章页码:771 - 783
Key words:aerial manipulators; back-stepping technology; fault-tolerant control; non-singular terminal sliding mode control; extended state observer
Abstract: In this paper, an active fault-tolerant control (FTC) strategy of aerial manipulators based on non-singular terminal sliding mode (NTSM) and extended state observer (ESO) is proposed. Firstly, back-stepping technology is adopted as the control framework to ensure the global asymptotic stability of the closed-loop system. Next, the NTSM with estimated parameters of actuator faults is used as main robustness controller to deal with actuator faults. Then, the ESO is utilized to estimate and compensate the complex coupling effects and external disturbances. The Lyapunov stability theory can guarantee the asymptotic stability of aerial manipulators system with actuator faults and external disturbances. The proposed FTC scheme considers both actuator fault and modelling errors, combined with the adaptive law of actuator fault, which has better performance than traditional FTC scheme, such as NTSM. Finally, several comparative simulations are conducted to illustrate the effectiveness of the proposed FTC scheme.
Cite this article as: DING Ya-dong, WANG Yao-yao, JIANG Su-rong, CHEN Bai. Active fault-tolerant control scheme of aerial manipulators with actuator faults [J]. Journal of Central South University, 2021, 28(3): 771-783. DOI: https://doi.org/10.1007/s11771-021-4644-7.

J. Cent. South Univ. (2021) 28: 771-783
DOI: https://doi.org/10.1007/s11771-021-4644-7
DING Ya-dong(丁亚东)1, WANG Yao-yao(王尧尧)1, 2, JIANG Su-rong(蒋素荣)1, CHEN Bai(陈柏)1
1. National Key Laboratory of Science and Technology on Helicopter Transmission,
Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;
2. The State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University,Hangzhou 310027, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract: In this paper, an active fault-tolerant control (FTC) strategy of aerial manipulators based on non-singular terminal sliding mode (NTSM) and extended state observer (ESO) is proposed. Firstly, back-stepping technology is adopted as the control framework to ensure the global asymptotic stability of the closed-loop system. Next, the NTSM with estimated parameters of actuator faults is used as main robustness controller to deal with actuator faults. Then, the ESO is utilized to estimate and compensate the complex coupling effects and external disturbances. The Lyapunov stability theory can guarantee the asymptotic stability of aerial manipulators system with actuator faults and external disturbances. The proposed FTC scheme considers both actuator fault and modelling errors, combined with the adaptive law of actuator fault, which has better performance than traditional FTC scheme, such as NTSM. Finally, several comparative simulations are conducted to illustrate the effectiveness of the proposed FTC scheme.
Key words: aerial manipulators; back-stepping technology; fault-tolerant control; non-singular terminal sliding mode control; extended state observer
Cite this article as: DING Ya-dong, WANG Yao-yao, JIANG Su-rong, CHEN Bai. Active fault-tolerant control scheme of aerial manipulators with actuator faults [J]. Journal of Central South University, 2021, 28(3): 771-783. DOI: https://doi.org/10.1007/s11771-021-4644-7.
1 Introduction
Unmanned aerial vehicles (UAVs) have been widely used in some fields, such as disaster rescue, electric inspection and geological detection [1, 2]. To improve the active interaction between the UAV and environment, the researchers mount a robotic manipulator on the UAV, the composite system is also known as the aerial manipulator [3, 4].
An aerial manipulator has the feature of multivariable, non-linear coupling and flexible structure, which leads to its poor stability and increases control difficulty. In flight, there are many kinds of disturbances, such as wind disturbance, engine vibration, which may lead to actuator faults. If actuator faults can not be detected effectively or the controller can not be handled in time within a limited control time, the aerial manipulator may lose control. The research on fault diagnosis and fault-tolerant control (FTC) of aerial manipulators becomes an urgent task toimprove its safety and reliability [5]. In recent years, some research results have been reported about the FTC [6, 7]. Generally, FTC methods can be classified into two categories: passive FTC and active FTC. Passive FTC method is similar to robust control in system construction, which uses a fixed controller to ensure that the closed-loop system is insensitive to specific faults and to maintain the stability of control system. The existing passive FTC methods have characters linear matrix inequality [8], linear quadratic [9], and variable structure control [10]. The passive FTC is easy to implement. However, with the increase of the number of possible failures and system redundancy, the controller design based on the passive method becomes more conservative, and the achievable control performance may not be satisfactory. Active FTC method is to redesign a control system based on the expected characteristics after faults occur, so that the fault system can keep stable [11]. The existing active FTC methods include multi model [12], adaptive control [13], pseudo inverse [14] and neural network [15].
In Ref. [16], a sliding mode observer and a sliding mode controller were designed, the sliding mode observer was used to estimate the fault information of the aircraft online, and then reconstructed the sliding mode controller. In Ref. [17], a sliding mode disturbance observer was designed to detect actuator faults, and the controller adjusted according to the fault information. In Ref. [18], several different fault observers were designed for sensor faults, and switched back and forth according to sensor faults. In Ref. [14], a model tracking reconstruction method based on the pseudo inverse was designed to ensure that the aircraft still has good model tracking performance under actuator faults. In Ref. [19], a fault detection estimation and fault tolerance integrated scheme of flight control system was designed based on Kalman filter method.
An aerial manipulator is a high-order differential system with multiple degree-of-freedom (DoF). The traditional control strategy may not be suitable for such high-order system, or can not achieve satisfactory control performance. It is found that the back-stepping control scheme provides a suitable control framework for such high-order systems [20, 21]. By constructing Lyapunov function, the high-order aerial manipulator system can be decomposed into several subsystems, and the controller structure of each subsystem is simple. When aerial manipulator system suffers actuator faults or strong external disturbances, back-stepping control can not guarantee good dynamic characteristics, other robust control strategies need to be combined to deal with dynamic estimated errors and external disturbances. Sliding mode control (SMC) can overcome the uncertainty of the system and has strong robustness to disturbances and un-modeled dynamics [22-26]. In Ref. [22], a non-singular terminal sliding mode (NTSM) was proposed to ensure the finite time convergence and avoid singularity of the system state. The robot movement, model uncertainties and external disturbances will worsen the tracking performance of the UAV system, an extended state observer (ESO) provides an effective method to estimate and compensate lumped external disturbances [27], the combination of ESO and SMC can not only estimate uncertainty accurately, but also get faster response [28].
The research on the FTC of the aerial manipulator is lacked, most of which was designed for UAV itself, ignoring the dynamic interaction effect between the main body and loading robotic manipulator. Besides, many existing FTC schemes of UAV were designed for attitude control, and ignoring position tracking, this paper focuses on the FTC of the aerial manipulator in flight trajectory tracking. Motivated by the previous discussion, in this paper, an active FTC scheme is proposed for the aerial manipulator system with actuator faults. The proposed FTC scheme mainly includes back-stepping control technique, NTSM and ESO. The back-stepping technique is used as the control framework, NTSM control is used to deal with the actuator faults in the final step of back-stepping procedure, the ESO is adopted to estimate and compensate the external disturbances and parameter uncertainty.
The main objectives of this paper are: 1) Combining the back-stepping technique and NTSM control to ensure the global asymptotic stability of the closed-loop system and improve the tracking performance; 2) Designing the adaptive law of actuator faults based on the proposed control scheme to estimate and compensate the actuator faults; 3) Adopting an ESO to deal with the lumped external disturbances; 4) Showing effectiveness of the proposed FTC scheme by several comparative simulations.
The paper is organized as follows. Section 2 describes the dynamic model of an aerial manipulator with actuator faults. In Section 3, the proposed FTC scheme is presented. In Section 4, the simulation model of an aerial manipulator is established, the effectiveness of the proposed FTC scheme is validated by several simulations. Finally, conclusions are given in Section 5.
2 Dynamic model
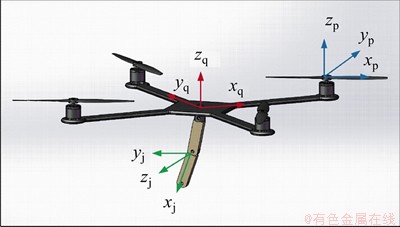
The dynamic model of the aerial manipulator mainly includes the dynamic model of the robot, the rigid-body dynamic model of the quadrotor UAV and the aerodynamic model. Four coordinate frames invloved in aerial manipulator system are depicted as Figure 1. The coordinate frame {Ob} denotes the body-fixed frame of the UAV; the coordinate frame {Oj} is the joint frame of the robot, the coordinate frame {Oe} denotes the end-effect or frame of the robot; the coordinate frame {Ow} represents the world frame;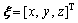 is the position vector of the UAV, rotation matrix R represents the attitude of the UAV constituted by the Euler angles
is the position vector of the UAV, rotation matrix R represents the attitude of the UAV constituted by the Euler angles 
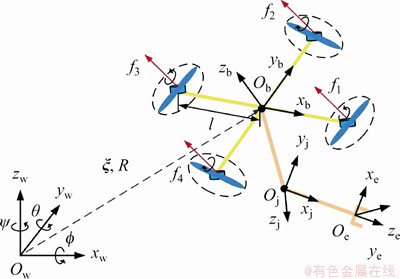
Figure 1 Coordinate frames involved in aerial manipulator system
For a robotic manipulator, the dynamic model can be written as [29]:
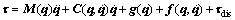 (1)
(1)
where 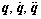 are the joint angle, joint velocity and joint acceleration vectors, respectively;
are the joint angle, joint velocity and joint acceleration vectors, respectively;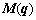 ,
, 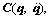
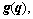
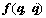 are the inertia matrix, Coriolis and centrifugal force, gravity torque and friction torque vector, respectively;
are the inertia matrix, Coriolis and centrifugal force, gravity torque and friction torque vector, respectively; 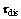 is the external disturbance torque; τ is the joint torque.
is the external disturbance torque; τ is the joint torque.
The rigid-body dynamic equation of the UAV can be described as [3]:
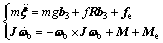 (2)
(2)
where m, J are the mass and inertia of the UAV, respectively; ωb is the angular velocity vector in body-fixed frame; f,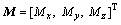 denotes the total thrust and moment vector in body-fixed frame;
denotes the total thrust and moment vector in body-fixed frame;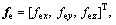
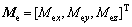 represent the external force and moment vector exerted by the robot movement and unknown disturbances, respectively; b3=[0 0 1]T; g represents the gravity acceleration. The control input
represent the external force and moment vector exerted by the robot movement and unknown disturbances, respectively; b3=[0 0 1]T; g represents the gravity acceleration. The control input 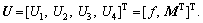
Generally speaking, the structure of quadrotor UAV is symmetrical, then the inertia of quadrotor UAV has 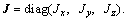 If the Euler angle of the UAV is small, we have
If the Euler angle of the UAV is small, we have 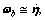 Eq. (2) can be extended as follows:
Eq. (2) can be extended as follows:
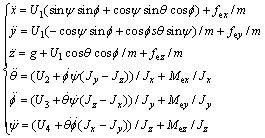 (3)
(3)
To facilitate the control design, the UAV system will be divided into two cascade subsystems, the position subsystem and attitude subsystem. Each subsystem is expressed as the form of state-space. As well-known, the state variables of attitude subsystem are independent, while the state variables of position subsystem depend on the state variables of attitude subsystem.
Using 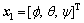 and
and as the state variables of the attitude subsystem, the state-space equation of the attitude subsystem can be written as:
as the state variables of the attitude subsystem, the state-space equation of the attitude subsystem can be written as:
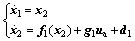 (4)
(4)
where 
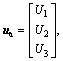
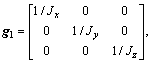

Using 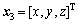 and
and 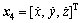 as the state variables of the position subsystem, the state-space equation of the position subsystem can be written as:
as the state variables of the position subsystem, the state-space equation of the position subsystem can be written as:
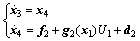 (5)
(5)
where 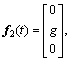
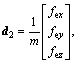
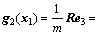

As shown in Eqs. (4) and (5), the UAV system has six state variables and only four control inputs, it is a typical under-actuated system. The position variables x and y need to be accomplished indirectly by the attitude angle. Usually, the position vector and the yaw angle 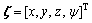 are regarded as the controlled variables and other Euler angle
are regarded as the controlled variables and other Euler angle 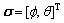 is treated as the intermediate variable. Therefore, except the thrust U1, the desired σd also need to be calculated from Eq. (5), therefore, Eq. (5) will be expressed as:
is treated as the intermediate variable. Therefore, except the thrust U1, the desired σd also need to be calculated from Eq. (5), therefore, Eq. (5) will be expressed as:
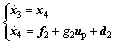 (6)
(6)
where up is the force vector in world frame,
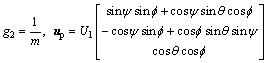 (7)
(7)
When desired yaw angle ψd is given, and thrust up is regulated by controller, then fd, θd and U1 can be calculated by Eq. (7).
In this paper, we focus on designing a control strategy to deal with the actuator faults of the UAV, the actuator faults include the loss of effectiveness fault and bias fault. A common description of actuator faults is:
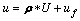 (8)
(8)
where is the bias fault vector;
is the bias fault vector; 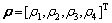 denotes the actuator effectiveness vector,
denotes the actuator effectiveness vector,  i=1, 2, 3, 4; and ρi=1 means that the i-th actuator works normally; 0<ρi<1 indicates that the working efficiency of i-th actuator is reduced; symbol * denotes numerical multiplication.
i=1, 2, 3, 4; and ρi=1 means that the i-th actuator works normally; 0<ρi<1 indicates that the working efficiency of i-th actuator is reduced; symbol * denotes numerical multiplication.
Combining the Eqs. (4) and (8), the state-space equation of the attitude subsystem with actuator faults can be expressed as
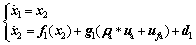 (9)
(9)
where 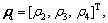
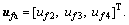
Combining Eqs. (5) and (8), the state-space equation of the position subsystem with actuator faults can be written as:
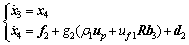 (10)
(10)
3 FTC scheme of aerial robot
For the aerial manipulator system, the UAV is the main body of motion and the robot is used for attitude control in flight. A cascade control structure including outer and inner loop is the most commonly used in control design, the attitude subsystem is internal loop and the position subsystem is the external loop, the control design procedure is as follows.
3.1 FTC scheme of attitude subsystem
Back-stepping control is a nonlinear system design method, by introducing virtual control variables, the complex high-order system is decomposed into many simpler and lower order systems [21], defining the attitude tracking error:
 (11)
(11)
where x1d is the desired attitude angle.
The first time derivative of e1 is:
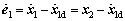 (12)
(12)
Defining angular velocity tracking error:
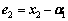 (13)
(13)
where α1 is virtual input variable to track e1.
Choosing  it has
it has
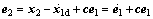 (14)
(14)
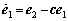 (15)
(15)
Using Eq. (9), it has:
 (16)
(16)
Considering the first Lyapunov function:
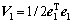 (17)
(17)
The first time derivative of V1 is:
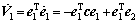 (18)
(18)
When then
then 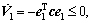 a NTSM strategy is adopted to stabilize the control system.
a NTSM strategy is adopted to stabilize the control system.
In the proof of stability, the following lemma 1 will be used.
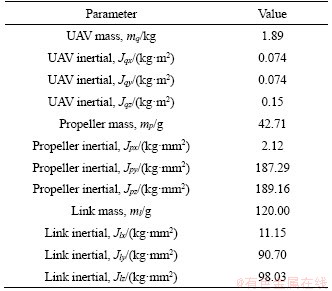
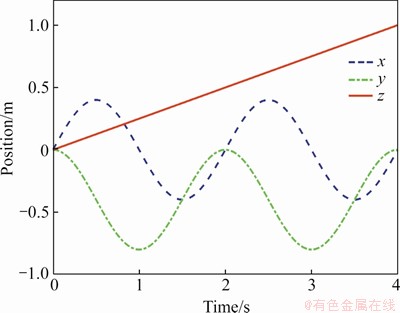
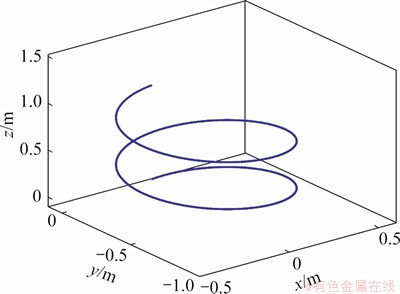
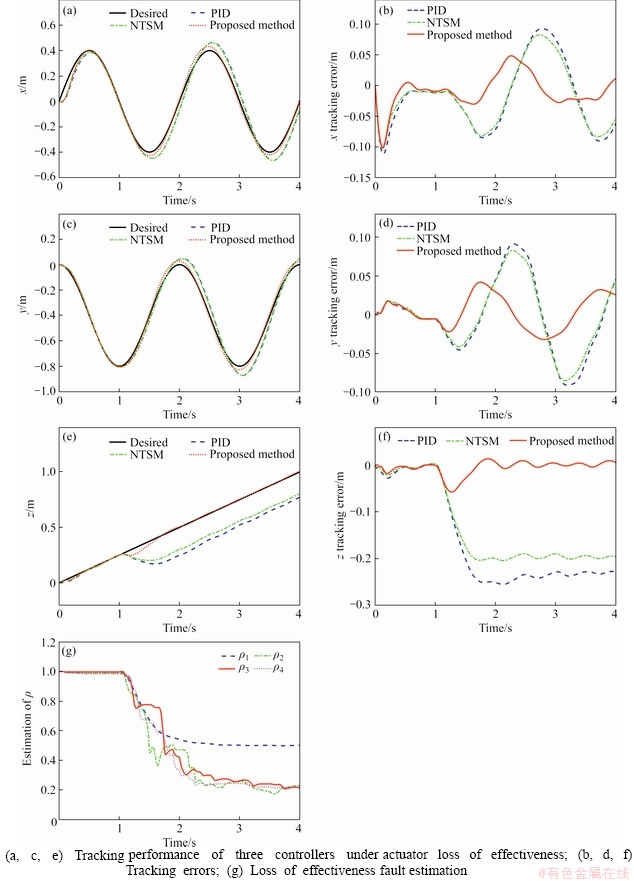
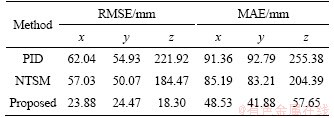
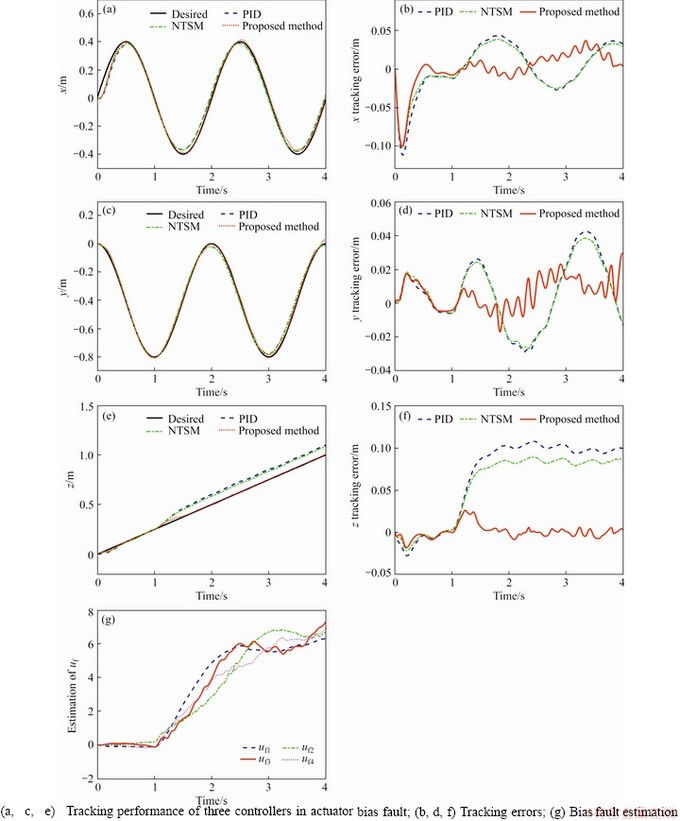
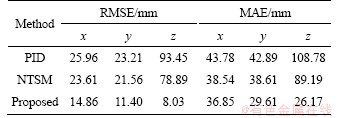
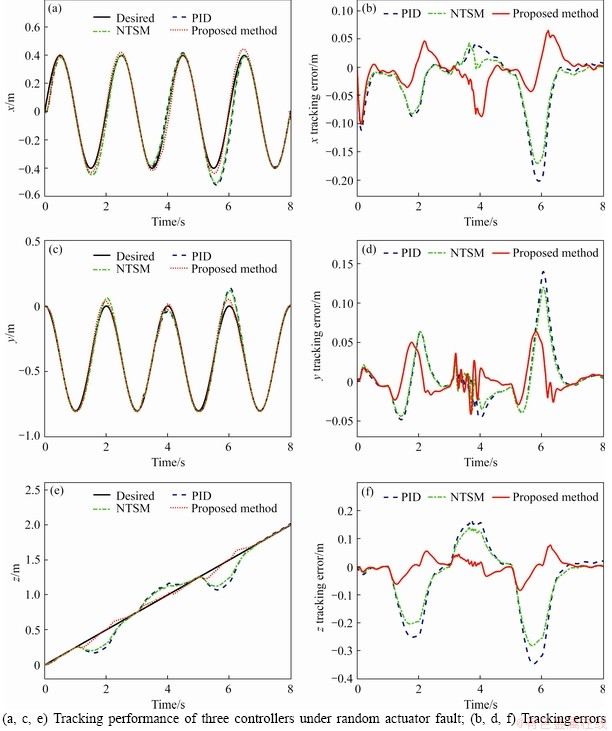
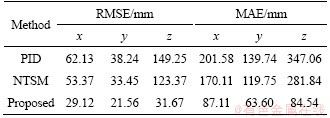
Lemma 1. If c1, c2, …, cn are positive numbers and 0 To simplify the expression, the following symbols are utilized in design of NTSM controller [22]. where The sliding surface of the attitude subsystem is defined as: where Combing Eqs. (16) and (20), the first time derivative of s can expressed as: Considering the second Lyapunov function V2: Using Eqs. (18) and (21), the first time derivative of V2 is: Regardless of external disturbance d1, with estimated actuator faults, the FTC of attitude subsystem is designed as: where Defining the third Lyapunov function V3: where When actuator fault parameters The first time derivative of V3 is: Substituting Eqs. (24) into (26), we have: Hence, the adaptation law of actuator faults is chosen as: Then, an ESO is adopted to estimate and compensate external disturbance d1, defining an extended state variable z3=d1, and its derivative where z1, z2, z3 are the output vectors of the ESO; e is the observation error; κ1, κ2, κ3are the observer gains. The nonlinear function where 0<ζ<1, v>0. The output variable z3 of the ESO is used as the estimated The remaining proof of stability is given in the appendix. 3.2 FTC scheme of position subsystem The FTC of position subsystem is similar to the FTC of attitude subsystem, defining the position tracking error, virtual control input and velocity tracking error, respectively. where The sliding surface of position subsystem is chosen as: A non-linear ESO is used to estimate and compensate the uncertainty d2. The adaptation law of actuator faults are designed as: Similar to Eq. (32), the thrust vector up is designed as The desired thrust U1d is calculated by projecting force vector up onto normal unit vector Rb3. The desired normal unit vector zb of the thrust is expressed as: i.e., If desired yaw angle ψd is given, fd, θd can be obtained by solving Eq. (43): 4 Simulations Several simulations are carried out on the aerial manipulator to validate the effectiveness of the proposed FTC scheme. The aerial manipulator consists of a quadrotor UAV and a two-link robot, the physical model of an aerial manipulator is built in Simulink by Simscape Multibody Toolbox [30]. The model of the aerial manipulator is shown in Figure 2. The quadrotor UAV system includes asymmetrical body-frame, four propellers and motors, the loading robotic manipulator consists of two identical links. The mass of aerial manipulator parts is uniformly distributed and the center of mass is at the geometric center. The physical parameters of each component of aerial manipulator are listed in Table 1. Figure 2 Model of aerial manipulator Table 1 Physical parameters of aerial manipulator The elliptical helix trajectory is used to demonstrate the effectiveness of the proposed controller, the desired trajectory is designed as follows, which are shown in Figures 3 and 4. pd=[0.4sin(πt), 0.4cos(πt)-0.4, 0.25t] m, ψd=0. The joint trajectory of two-link robot is sinusoidal curve q=π/3sin(2πt) rad, the motion of the robotic manipulator can be regarded as the external disturbance to validate the robustness of the proposed control scheme. Three cases of actuator faults are described to illustrate the proposed method. Case 1 assumes that actuator loss of effectiveness occurs at 1 s; Case 2 assumes that actuator bias fault occurs at 1 s; Case 3 assumes that actuator loss of effectiveness and bias fault occur at specified time after 1 s. The first two cases are used to validate the adaptive law and tracking performance under specific faults, the third case is designed to reveal the tracking performance of the proposed FTC strategy under random faults. Figure 3 Elliptical helix Figure 4 Elliptical helix in Cartesian space For Case 1: For Case 2: For Case 3: Three controllers, i.e., a conventional PID controller, a NTSM controller and a proposed controller are used to demonstrate the effectiveness of proposed FTC strategy. For the PID controller, the control parameters of position subsystem are kp=diag(80, 80, 80), kd=diag(26, 26, 26), ki=diag(3, 3, 3), the control parameters of the attitude subsystem are selected as kp=diag(220, 220, 450), kd=diag(9, 9, 20), ki=diag(6, 6, 8). For NTSM controller, control parameters of position subsystem are chosen as γ=diag(3, 3, 3), λ=diag(0.8, 0.8, 0.8), μ=diag(1.2, 1.2, 1.2), b1=diag(20, 20, 20), b2=diag(4, 4, 4), the control parameters of the attitude subsystem are chosen as γ=diag(25, 25, 25), λ=diag(0.8, 0.8, 0.8), μ=diag(1.2, 1.2, 1.2), b2=diag(10, 10, 10), b1=diag(300, 300, 300). For the proposed controller, the parameters of NTSM part are the same, the parameters of adaptive law in positon subsystem are δ=10, σ=8, the parameters of adaptive law in attitude subsystem are δ=5, σ=1. The parameters of ESO are κ1=diag(50, 50, 50), ζ2=diag(0.25), ζ1=0.5, v=0.3, κ3=diag(2000, 2000, 2000), κ2=diag(500, 500, 500). For Case 1, the actuator loss of effectiveness occurs at 1 s, the tracking performance of three controllers under actuator loss of effectivenessis shown in Figure 5. The root mean square error (RMSE) and maximum absolute error (MAE) of three controllers are listed in Table 2 (only collecting data after actuator faults occur). The tracking errors of NTSM controller are slightly lower than that of PID controller. To be specific, compared with PID controller, RMSE reduced by 8.07%, 8.85% and 16.87% respectively, and MAE reduced by 6.75%, 10.32% and 19.97% respectively. The data show the robustness of NTSM. However, for both controllers, as shown in Figure 5, the tracking errors increase rapidly and can not converge when actuator loss of effectiveness occurs. Therefore, the simple robust control strategy can not guarantee system stability of the aerial manipulator under actuator loss of effectiveness. Compared with PID controller and NTSM controller, the tracking errors of the proposed FTC strategy are reduced obviously, and the system can recover stability under actuator loss of effectiveness. To be specific, compared with PID controller, RMSE reduced by 61.51%, 55.45% and 91.75%, respectively, and the MAE reduced by 46.88%, 54.87% and 77.43%, respectively. As shown in Figure 5(g), the estimated actuator loss of effectiveness is close to the real value, the residual estimation error is mainly caused by modeling error and disturbance exerted by robot movement. Figure 5 Case 1: Table 2 Tracking errors of Case 1 For Case 2, the actuator bias fault occurs at 1 s, the tracking performance of three controllers under actuator bias fault is shown in Figure 6. Similar to Case 1, for the PID controller and the NTSM controller, the tracking errors are not convergent when actuator bias fault occurs. RMSE and MAE of three controllers are shown in Table 3. Tracking performance of NTSM controller is slightly superior to that of PID controller. To be specific, compared with PID controller, RMSE reduced by 9.05%, 7.11% and 15.58%, respectively, and MAE reduced by 11.97%, 9.98% and 18.01%, respectively. As shown in Figure 6, the tracking performance of the proposed FTC strategy is improved, and the system can recover stability after actuator bias fault occurs. To be specific, compared with PID controller, the RMSE reduced by 42.76%, 50.88%, 91.41%, respectively, and the MAE reduced by 15.83%, 30.96%, 75.94%, respectively. As shown in Figure 6(g), the estimated actuator bias fault is close to the real value after actuator fault occurs, the estimated residual is caused by modelling error and disturbance exerted by robot movement. For Case 3, in order to demonstrate the tracking performance of aerial manipulator under random actuator fault, the simulation time is increased to 8 s. The tracking performance of three controllers under random actuator fault is shown in Figure 7. RMSE and MAE of three controllers are shown in Table 4. The tracking performance of NTSM controller is slightly superior to than that of PID controller. Compared with PID controller and NTSM controller, the tracking errors of the proposed FTC strategy are reduced remarkably, and can recover stability quickly after actuator fault occurs. To be specific, compared with PID controller, RMSE reduced by 53.13%, 43.62% and 78.78%, respectively, and MAE reduced by 56.78%, 54.49% and 75.6%, respectively. The simulation results show the proposed FTC scheme has good performance under actuator loss of effectiveness and bias fault. 5 Conclusions In this paper, an active FTC scheme is proposed for aerial manipulators with actuator faults. The back-stepping design method is used as the control framework, then, the NTSM is designed to deal with the actuator faults and the ESO is adopted to compensate the complex coupling effects between the UAVs and the robotic manipulator and external disturbances. The proposed FTC method can guarantee the asymptotic stability of the closed-loop control system. Finally, several comparative simulations are carried out to illustrate the effectiveness of the proposed approach. In the future, we will carry out experimental validation of the proposed FTC scheme on our own aerial manipulator under actuator loss of effectiveness and bias fault. The gain parameters of ESO are selected to estimate the model error and disturbance by experiment test. Then, the gain parameters of NSTM and adaptive law are chosen by executing actuator fault experiment. With comparison results between simulation and experiment of FTC scheme, we will have a better understanding of the proposed FTC method in practice. The experiment results will offer a basis for improving proposed FTC scheme. Figure 6 Case 2: Table 3 Tracking errors of Case 2 Figure 7 Case 3: Table 4 Tracking errors of Case 3 Appendix The remaining proof of stability is given as follows: Substituting Eq. (32) into Eq. (27), combing Eqs. (28) and (29), we have: where Equation (46) can be rewritten as follows: where Using Lemma 1, Eq. (47) can be expressed as: If For Eq. (48), by similar analysis, if Combining Eqs. (49) and (50), sliding surface si will converge to the following region: When the sliding surface converges, the tracking error ei will also converges, and then the proof is completed. Contributors DING Ya-dong and WANG Yao-yao provided the concept of the topics. DING Ya-dong conducted the literature review and wrote the first draft of the manuscript. JIANG Su-rong and CHEN Bai edited the draft of manuscript. All authors replied to reviewers’ comments and revised the final version. Conflict of interest DING Ya-dong, WANG Yao-yao, JIANG Su-rong and CHEN Bai declare that they have no conflict of interest. References [1] NGUYEN H N, PARK S, PARK J, LEE D. A novel robotic platform for aerial manipulation using quadrotors as rotating thrust generators [J]. IEEE Transactions on Robotics, 2018, 34(2): 353-369. DOI:10.1109/TRO.2018.2791604. [2] LEE H, KIM H J. Estimation, control, and planning for autonomous aerial transportation [J]. IEEE Transactions on Industrial Electronics, 2017, 64(4): 3369-3379. DOI: 10.1109/TIE.2016.2598321. [3] FANNI M, KHALIFA A. A new 6-DOF quadrotor manipulation system: Design, kinematics, dynamics, and control [J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(3): 1315-1326. DOI: 10.1109/TMECH.2017.2681179. [4] DING Ya-dong, WANG Yao-yao, CHEN Bai. A practical time-delay control scheme for aerial manipulators [J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2021, 235(3): 371-388. DOI: 10.1177/0959651820946511. [5] ZHENG Feng-ying, ZHEN Zi-yang, GONG Hua-jun. Observer-based backstepping longitudinal control for carrier-based UAV with actuator faults [J]. Journal of Systems Engineering and Electronics, 2017, 28(2): 322-377. DOI: 10.21629/JSEE.2017.02.14. [6] CAO Lu, XIAO Bing, GOLESTANI M. Robust fixed-time attitude stabilization control of flexible spacecraft with actuator uncertainty [J]. Nonlinear Dynamics, 2020, 100(3): 2505-2519. DOI: 10.1007/s11071-020-05596-5. [7] XIAO Bing, CAO Lu, XU Sheng-yuan, LIU Liang. Robust tracking control of robot manipulators with actuator faults and joint velocity measurement uncertainty [J]. IEEE/ASME Transactions on Mechatronics, 2020, 25(3): 1354-1365. DOI: 10.1109/TMECH.2020.2975117. [8] HESS R A, WELLS S R. Sliding mode control applied to reconfigurable flight control design [J]. Journal of Guidance, Control, and Dynamics, 2003, 26(3): 452-462. DOI: 10.2514/2.5083. [9] VEILLETTE R J. Reliable linear-quadratic state-feedback control [J]. Automatica, 1995, 31(1): 137-143. DOI: 10.1016/0005-1098(94)E0045-J. [10] KIM D, KIM Y. Robust variable structure controller design for fault tolerant flight control [J]. Journal of Guidance, Control, and Dynamics, 2000, 23(3): 430-437. DOI: 10.2514/2.4577. [11] BAJPAI G, CHANG B C, LAU A. Reconfiguration of flight control systems for actuator failures [J]. IEEE Aerospace and Electronic Systems Magazine. 2001, 16(9): 29-33. DOI: 10.1109/62.949534. [12] YEN G G, HO L W. On-line multiple-model based fault diagnosis and accommodation [C]// Proceeding of the 2001 IEEE International Symposium on Intelligent Control (ISIC '01) (Cat No 01CH37206). 2001: 73-78. DOI: 10.1109/ ISIC.2001.971487. [13] KIM K S, LEE K J, KIM Y. Reconfigurable flight control system design using direct adaptive method [J]. Journal of Guidance, Control, and Dynamics, 2003, 26(4): 543-550. DOI: 10.2514/2.5103. [14] GAO Zhi-qiang, ANTSAKLIS P J. Stability of the pseudo-inverse method for reconfigurable control systems [J]. International Journal of Control, 1991, 53(3): 717-729. DOI: 10.1080/00207179108953643. [15] NAPOLITANO M R, AN Y, SEANOR B A. A fault tolerant flight control system for sensor and actuator failures using neural networks [J]. Aircraft Design, 2000, 3(2): 103-128. DOI: 10.1016/S1369-8869(00)00009-4. [16] SHTESSEL Y, BUFFINGTON J, BANDA S. Multiple timescale flight control using reconfigurable sliding modes [J]. Journal of Guidance, Control, and Dynamics, 1999, 22(6): 873-883. DOI: 10.2514/2.4465. [17] BESNARD L, SHTESSEL Y B, LANDRUM B. Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer [J]. Journal of the Franklin Institute, 2012, 349(2): 658-684. DOI: 10.1016/ j.jfranklin.2011.06.031. [18] STOUSTRUP J, GRIMBLE M J, NIEMANN H. Design of integrated systems for the control and detection of actuator/sensor faults [J]. Sensor Review, 1997, 17(2): 138-149. DOI: 10.1108/02602289710170311. [19] AMOOZGAR M H, CHAMSEDDINE A, ZHANG You-min. Experimental test of a two-stage Kalman filter for actuator fault detection and diagnosis of an unmanned quadrotor helicopter [J]. Journal of Intelligent & Robotic Systems, 2013, 70(1-4): 107-117. DOI: 10.1007/s10846-012-9757-7. [20] LI Jun-peng, YANG Ya-na, HUA Chang-chun, GUAN Xin-ping. Fixed-time backstepping control design for high-order strict-feedback non-linear systems via terminal sliding mode [J]. IET Control Theory & Applications, 2017, 11(8): 1184-1193. DOI: 10.1049/iet-cta.2016.1143. [21] SU Qing-yu, QUAN Wan-zhen, CAI Guo-wei, LI Jian. Improved adaptive backstepping sliding mode control for generator steam valves of non-linear power systems [J]. IET Control Theory & Applications, 2017, 11(9): 1414-1419. DOI: 10.1049/iet-cta.2016.1241. [22] YU Shuang-he, YU Xing-huo, SHIRINZADEH B, MAN Zhi-hong. Continuous finite-time control for robotic manipulators with terminal sliding mode [J]. Automatica, 2005, 41(11): 1957-1964. DOI: 10.1016/j.automatica. 2005.07.001. [23] WANG Yao-yao, LIU Lu-fang, WANG Dan, JU Feng, CHEN Bai. Time-delay control using a novel nonlinear adaptive law for accurate trajectory tracking of cable-driven robots [J]. IEEE Transactions on Industrial Informatics, 2020, 16(8): 5234-5243. DOI: 10.1109/TII.2019.2951741. [24] WANG Yao-yao, YAN Fei, CHEN Jia-wang, JU Feng, CHEN Bai. A new adaptive time-delay control scheme for cable-driven manipulators [J]. IEEE Transactions on Industrial Informatics, 2019, 15(6): 3469-3481. DOI: 10.1109/TII.2018.2876605. [25] WANG Yao-yao, LI Shi-zhen, WANG Dan, JU Feng, CHEN Bai, WU Hong-tao. Adaptive time-delay control for cable-driven manipulators with enhanced nonsingular fast terminal sliding mode [J]. IEEE Transactions on Industrial Electronics, 2021, 68(3): 2356-2367. DOI: 10.1109/ TIE.2020.2975473. [26] WANG Yao-yao, GU Lin-yi, XU Yi-hong, CAO Xiao-xu. Practical tracking control of robot manipulators with continuous fractional-order nonsingular terminal sliding mode [J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6194-6204. DOI: 10.1109/TIE.2016.2569454. [27] YIN Li-jian, XIA Yuan-qing, DENG Zhi-hong, HUO Bao-yu. Extended state observer-based attitude fault-tolerant control of rigid spacecraft [J]. International Journal of Systems Science, 2018, 49(12): 2525-2535. DOI: 10.1080/ 00207721.2018.1498556. [28] PUKDEBOON C. Extended state observer-based third-order sliding mode finite-time attitude tracking controller for rigid spacecraft [J]. Science China Information Sciences, 2018, 62(1): 1-16. DOI: 10.1007/s11432-017-9389-9. [29] DING Li, LI Xing-cheng, LI Qi-lin, CHAO Yuan. Nonlinear friction and dynamical identification for a robot manipulator with improved cuckoo search algorithm [J]. Journal of Robotics, 2018, 2018: 1-10. DOI: 10.1155/2018/8219123. [30] The Math Works [M]. Natwik, Massachusetts: Matlab User’s Guide, 1995. (Edited by ZHENG Yu-tong) 中文导读 执行器故障下飞行机械臂的主动容错控制 摘要:本文提出了一种基于非奇异终端滑模和扩展状态观测器的飞行机械臂主动容错控制方法。首先,采用反演技术作为闭环控制框架,保证系统的全局稳定性。其次,采用自适应非奇异终端滑模作为执行器故障下的鲁棒控制器。然后,利用扩展状态观测器对复杂的耦合效应和外部干扰进行估计和补偿。李雅普诺夫稳定性理论可以保证具有执行器故障和外部干扰的飞行机械臂系统的渐近稳定性。本文提出的主动容错控制方案综合考虑了执行器故障和建模误差,并结合执行器故障的自适应律,其性能优于传统的容错控制方法。最后,通过多个仿真对比,验证了所提出的主动容错控制方案的有效性。 关键词:飞行机械臂;反演技术;容错控制;非奇异终端滑模控制;扩展状态观测器 Foundation item: Project(51705243) supported by National Natural Science Foundation of China; Project(NS2020052) supported by the Fundamental Research Funds for the Central Universities, China; Project(GZKF-201915) supported by the Open Foundation of the State Key Laboratory of Fluid Power and Mechatronic Systems, China Received date: 2020-06-06; Accepted date: 2020-12-14 Corresponding author: WANG Yao-yao, PhD, Associate Professor; Tel: +86-25-84892503; E-mail: yywang_cmee@nuaa.edu.cn; ORCID: https://orcid.org/0000-0001-5237-378X; JIANG Su-rong, PhD, Lecture; Tel: +86-25-84892503; E-mail: jsrong@nuaa.edu.cn; ORCID: https://orcid.org/0000-0001-6893-406X (19)
(19)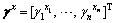 ,
, 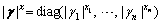 ,
,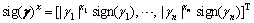

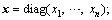 n is the number of dimension.
n is the number of dimension.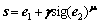 (20)
(20)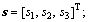

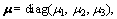
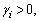
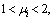 i=1, 2, 3 are design parameters.
i=1, 2, 3 are design parameters.
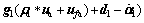 (21)
(21)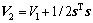 (22)
(22)
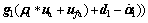 (23)
(23)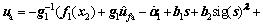
 (24)
(24) is the estimated value of ρa; the estimated error of ρa is
is the estimated value of ρa; the estimated error of ρa is 
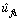 is the estimated value of
is the estimated value of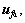 estimated error of
estimated error of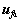 is
is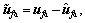
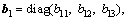
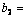
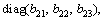
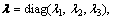

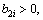 0< λi<1 for i=1, 2, 3.
0< λi<1 for i=1, 2, 3. (25)
(25)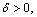
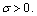
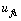 and
and 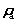 are constant, then
are constant, then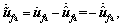
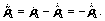
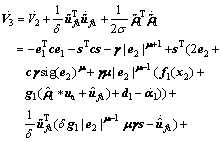
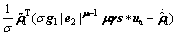 (26)
(26)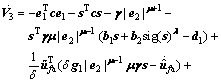
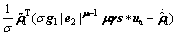 (27)
(27)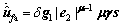 (28)
(28)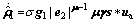 (29)
(29)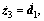 a non-linear ESO is constructed as:
a non-linear ESO is constructed as: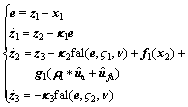 (30)
(30)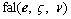 is defined as:
is defined as: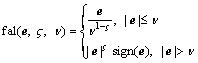 (31)
(31)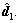 When the gain parameters of the ESO are selected properly, the estimated
When the gain parameters of the ESO are selected properly, the estimated is close to
is close to 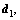 and the FTC of attitude subsystem is modified to:
and the FTC of attitude subsystem is modified to: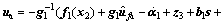
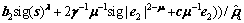 (32)
(32) (33)
(33)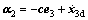 (34)
(34)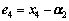 (35)
(35)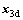 is the desired position input.
is the desired position input.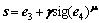 (36)
(36)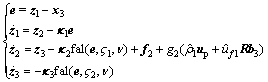 (37)
(37)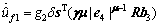 (38)
(38)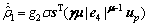 (39)
(39)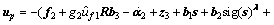
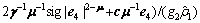 (40)
(40)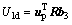 (41)
(41) (42)
(42)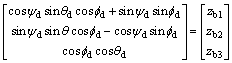 (43)
(43) (44)
(44) (45)
(45)

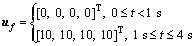



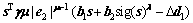 (46)
(46)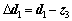 is the observation error.
is the observation error.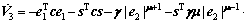
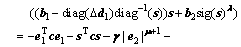
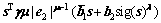 (47)
(47)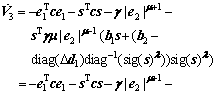
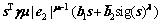 (48)
(48)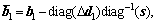
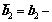
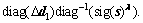

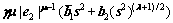 (49)
(49)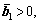 i.e.,
i.e., 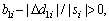 i=1, 2, 3, then
i=1, 2, 3, then  the control system is stable. Therefore, sliding surface si will converge to the following region:
the control system is stable. Therefore, sliding surface si will converge to the following region: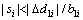 (50)
(50)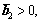 i.e.,
i.e.,  i=1, 2, 3, then
i=1, 2, 3, then 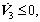 the control system is stable. We have:
the control system is stable. We have: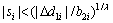 (51)
(51) (52)
(52)

