磨削面齿轮粗糙表面最小润滑膜厚分析
严宏志1,张龙赐1,何国旗1,2,胡威1
(1. 中南大学 高性能复杂制造国家重点实验室,湖南 长沙,410083;
2. 湖南工业大学 机械工程学院,湖南 株洲,412000)
摘要:根据齿轮啮合原理,推导传动接触轨迹点的方程。利用微分几何原理求出啮合点处两齿轮的主曲率。结合有限元分析方法,求得啮合过程中齿面的法向接触力。由齿面相对运动原理,计算正交面齿轮传动中的齿面卷吸速度。运用点接触Dowson-Higginson最小膜厚公式计算出光滑齿面啮合过程中的最小油膜厚度。基于磨削齿面形貌的分析,引入最小油膜厚度修正因子,计算出齿面不同形貌润滑状态下最小油膜厚度。研究结果表明:面齿轮从进入啮合到脱离啮合过程中,最小油膜厚度逐渐增大,单齿啮合与双齿啮合交界处出现拐点,其最大值出现在靠近齿根的啮合点处。在计算的粗糙度范围内,增大粗糙度使最小油膜厚度增大。磨削齿面在靠近齿根处的啮合点有最大表面方向参数,且使该点在不同粗糙度下最小油膜厚度的变化最小。本研究为面齿轮设计及其润滑失效分析提供重要依据。
关键词:磨削加工;面齿轮;表面形貌;油膜厚度;修正因子
中图分类号:TH117.2 文献标志码:A 文章编号:1672-7207(2013)12-4861-08
Minimum lubricant film thickness of rough surface in grinding face-gear
YAN Hongzhi1, ZHANG Longci1, HE Guoqi1, 2, HU Wei1
(1. State Key Laboratory of High Performance Complex Manufacturing,Central South University, Changsha 410083, China;
2. School of Mechanical Engineering, Hunan University of Technology, Zhuzhou 412000, China)
Abstract: Based on the face-gear generation process, the tooth surface curvature of face-gear was obtained, and the equation of the contact points on the face gear was deduced. According to differential geometry theory, the principal curvatures of the contact points on the pinion and the face gear were calculated. Using ABAQUS,the simulation results of normal contact force were got. The tooth surface relative velocity of orthogonal face-gear drive was achieved. Based on Dowson-Higginson equation, Minimum film thickness of smooth tooth surface in meshing process was obtained. According to the effect of grinding method to surface topography, the minimum film thickness correction factor is recommended, and minimum film thickness of lubrication in the tooth surfaces considering diverse rough surface was analyzed. From the beginning of meshing process to its disengagement, the minimum film thickness increases gradually. Its inflection point appears between the double teeth-meshing area and the single teeth-meshing area, and its maximum appears when the contact point is closes to the root of face gear. In the range of computing roughness, the minimum film thickness increases while surface roughness increases. The contact point near root in grinding wheel has maximum surface pattern parameter, and the minimum film thickness of this point has the least variation. This study provides important basis for the design and the lubricant deficiency analysis of face gear.
Key words: grinding machining; face-gear; surface topography; film thickness; correction factor
与螺旋锥齿轮相比,面齿轮应用于直升机主传动系统具有结构简单、质量轻、噪声小、传动重合度大、动力分流效果好、振动小等优点[1]。面齿轮传动被称为“21世纪旋翼机传动之希望所在”[2]。齿轮的表面形貌对齿轮润滑有直接影响,由此影响齿轮啮合噪声、振动与磨损[3]。一些国内外学者对粗糙齿面的润滑特性进行了相关研究。如英国Cardiff大学齿轮摩擦学研究小组采用有限元对两表面粗糙度的均方根值σ>0.41 μm的横向条纹粗糙表面的线接触混合弹流润滑问题进行了数值研究,求出与齿轮传动实际情况相近的齿面压力分布、油膜厚度和接触区表面应力分布[4-5]。冯桂萍等[6]对粗糙齿面啮合的热弹流润滑进行了研究,分析了一对轮齿从进入啮合到脱离啮合的整个啮合过程中最大主剪应力和平均油膜厚度的变化规律。畅通等[7]对考虑粗糙度的直齿圆柱齿轮的热混合润滑特性进行了分析。在一般粗糙表面润滑成膜机理与特征方面的研究更加丰富,但由于面齿轮设计制造技术的研究开展时间较短,关于面齿轮齿面表面形貌对其润滑特性的影响研究还未见报道。本文作者在分析面齿轮不同啮合点处卷吸速度、曲率半径、法向接触力变化的基础上,引入最小油膜修正因子,分析了具有磨削加工表面特征的面齿轮啮合过程中的最小油膜厚度,为面齿轮设计制造技术及其啮合性能分析提供依据。
1 面齿轮啮合接触特性分析
面齿轮粗糙齿面的润滑机制分析需基于如下过程。
1.1 齿面接触轨迹方程
面齿轮加工坐标系如图1所示,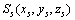 和
和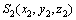 为随刀具和面齿轮一起转动的坐标系,
为随刀具和面齿轮一起转动的坐标系,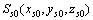 和
和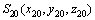 为刀具和面齿轮初始位置的固定坐标系,刀具转动角度为
为刀具和面齿轮初始位置的固定坐标系,刀具转动角度为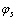 ,面齿轮转动角度为
,面齿轮转动角度为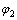 。将坐标系中所有刀具参数替换为小齿轮(与面齿轮啮合的圆柱齿轮)参数。得到随小齿轮转动的坐标系
。将坐标系中所有刀具参数替换为小齿轮(与面齿轮啮合的圆柱齿轮)参数。得到随小齿轮转动的坐标系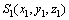 ,小齿轮初始位置固定的坐标系
,小齿轮初始位置固定的坐标系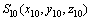 ,小齿轮转动角度为
,小齿轮转动角度为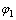 。根据面齿轮加工坐标系,以及刀具齿面、小齿轮齿面、面齿轮齿面的啮合关系,由坐标变换可得面齿轮在坐标系S2下的接触轨迹方程为[8]:
。根据面齿轮加工坐标系,以及刀具齿面、小齿轮齿面、面齿轮齿面的啮合关系,由坐标变换可得面齿轮在坐标系S2下的接触轨迹方程为[8]:
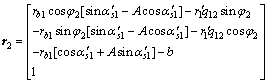 (1)
(1)
式中:rb1为小齿轮基圆半径;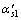 为刀具与圆柱齿轮的啮合角;
为刀具与圆柱齿轮的啮合角; ,
,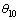 为小齿轮齿槽对称线与渐开线起始点的角度夹角;
为小齿轮齿槽对称线与渐开线起始点的角度夹角;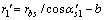 ,b为刀具和小齿轮中心距,rbs为刀具渐开线基圆半径;q12为小齿轮与面齿轮齿数比,
,b为刀具和小齿轮中心距,rbs为刀具渐开线基圆半径;q12为小齿轮与面齿轮齿数比,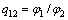 。面齿轮上的啮合轨迹为一条以
。面齿轮上的啮合轨迹为一条以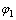 为参数的空间曲线。
为参数的空间曲线。
实例面齿轮副基本参数为:模数m=5,刀具齿数ns=20,小齿轮齿数n1=17,面齿轮齿数n2=100,分度圆压力角α=25°。r2的前3个分量对应啮合点的3个坐标,得啮合过程中面齿轮齿面上由齿顶向齿根方向上10个啮合点坐标,如表1所示,啮合点在面齿轮齿面位置如图2所示。
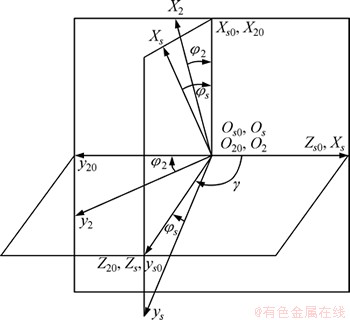
图1 面齿轮加工坐标系
Fig. 1 Coordinate system for face-gear Generation process
表1 啮合点坐标
Table 1 Coordinate of meshing point mm
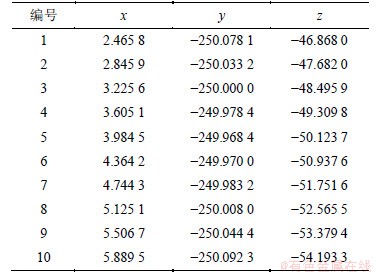
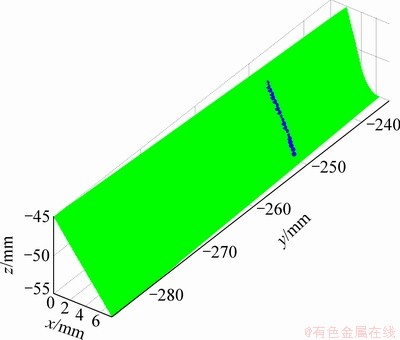
图2 面齿轮齿面啮合点
Fig. 2 Meshing point on face-gear
啮合点轨迹的切线方向即为齿面卷吸速度方向,啮合轨迹与磨削接触轨迹确定了面齿轮的表面方向 参数。
1.2 齿轮曲率分析
根据微分几何原理,设曲面方程用参数u和v表示为r=r(u,v),则曲面的法矢量n为:
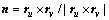 (2)
(2)
此曲面上点p(u,v)沿λ=du/dv方向的法曲率K可表示为:
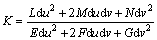 (3)
(3)
式中: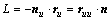 ;
; ;N=
;N=  ;
;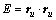 ;
;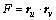 ;
;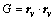 。
。
对于曲面上的固定点,E,F,G和L,M,N为常数,其法曲率存在的2个极值即为主曲率,记为K1和K2。主曲率满足下面方程[8]:
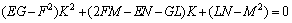 (4)
(4)
小齿轮轮廓为渐开线,利用上述基本原理可求得啮合点处主曲率为:
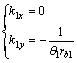 (5)
(5)
式中:θ1为小齿轮齿面参数;rb1为小齿轮基圆半径。
由面齿轮齿面向量和齿面法向量的表达式[8],求导可得曲率计算所需各个参数,结合面齿轮某一点的参数φs和θs,θs为刀具渐开线某点角度参数,可求得该点的2个主曲率k2x和k2y,所取10个啮合点对应主曲率如表2所示。
表2 啮合点主曲率
Table 2 Principal curvature of meshing point
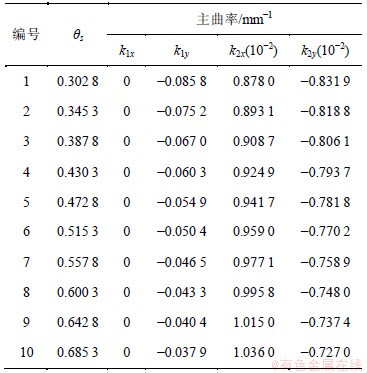
由主曲率可得综合曲率半径,从而求解10个啮合点最小润滑油膜膜厚公式中的椭圆参数。
1.3 齿面卷吸速度分析
齿面相对速度是指啮合点在运动坐标系内沿齿面的运动速度,它与啮合点轨迹相切,是面齿轮润滑计算的重要参数之一。设小齿轮和面齿轮上啮合点相对速度分别为v1和v2,由啮合线分别在两齿面上的轨迹方程可得到齿面相对速度,小齿轮的齿面相对速度为[9]:
 (6)
(6)
面齿轮的齿面相对速度为:
 (7)
(7)
式中: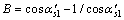 ;
; ;
; 。
。
齿面卷吸速度v为2个齿轮表面沿啮合点切线方向速度的一半,小齿轮转速为400 rad/s,得齿面卷吸速度如图3所示。由图3可知:面齿轮齿面卷吸速度随着小齿轮转动而逐渐增大。
面齿轮的润滑由啮合齿面的曲率、卷吸速度、轮齿承受的载荷等因素决定,与其他类型的齿轮传动相比,面齿轮在啮合时齿面卷吸速度很高,对润滑成膜有积极意义。
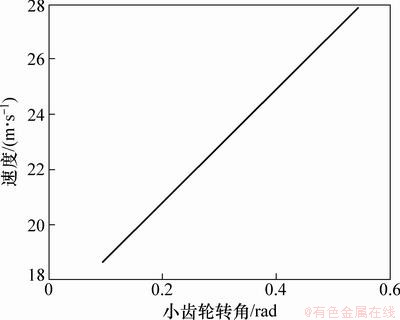
图3 齿面卷吸速度
Fig. 3 Entrainment velocity of tooth surface
2 面齿轮法向接触力有限元分析
采用圆柱齿轮驱动面齿轮的方法,在有限元ABAQUS分析软件中对面齿轮有限元模型进行加载啮合仿真,5齿有限元模型如图4所示。

图4 面齿轮啮合5齿有限元模型
Fig. 4 Finite element model of five meshing teeth
面齿轮所受阻力矩为500 N·m,2个齿轮选用相同材料,弹性模量E=2.06×1011 Pa,泊松比v=0.3,面齿轮啮合过程中接触面为曲面,通过接触压强来求法向载荷,以5齿有限元模型的中间齿第3齿为研究对象,其啮合过程中某一时刻接触区接触压强云图如图5所示。则此时法向接触力为:
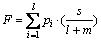 (8)
(8)
式中:pi为接触区某点的接触压强;s为接触面积;l为第3齿接触区节点数;m为第4齿接触区节点数。
设小齿轮与中间齿开始啮合时小齿轮转角为零,整个啮合过程中,中间齿法向接触力随小齿轮转角变化如图6所示。
面齿轮传动过程中,进入和脱离啮合均为双齿啮合。双齿啮合变单齿啮合时,齿面法向接触力急剧增大,并在一定范围内波动。
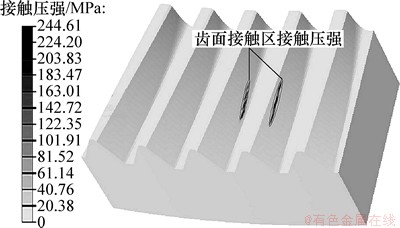
图5 齿面接触压强云图
Fig. 5 Clouds of contact pressure in tooth surface
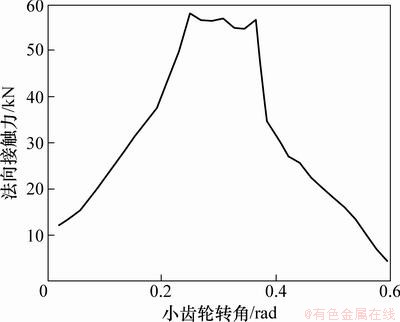
图6 中间齿啮合过程中法向接触力
Fig. 6 Normal contact force of middle tooth in engagement process
3 面齿轮磨削接触迹离散点分析
图7所示为面齿轮磨削加工坐标系。其中,插齿刀静坐标系为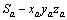 ,随动坐标系为
,随动坐标系为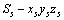 ,绕轴线
,绕轴线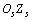 旋转,转速为
旋转,转速为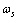 ,转角为
,转角为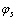 ;基蜗杆静坐标系为
;基蜗杆静坐标系为 ,随动坐标系为
,随动坐标系为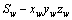 ,绕轴线
,绕轴线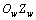 旋转,转速为
旋转,转速为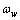 ,转角为
,转角为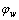 ;面齿轮静坐标系为
;面齿轮静坐标系为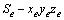 ,随动坐标系为
,随动坐标系为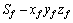 ,绕轴线
,绕轴线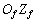 旋转,转速为
旋转,转速为 ,转角为
,转角为 。
。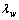 为砂轮的导程角,
为砂轮的导程角,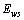 为基蜗杆到插齿刀轴线之间最短距离。
为基蜗杆到插齿刀轴线之间最短距离。
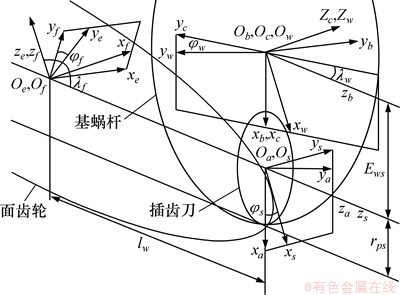
图7 面齿轮磨削加工坐标系
Fig. 7 Coordinate of grinding machining face-gear
利用加工面齿轮插齿刀齿面作为产形面,由包络原理可得到基蜗杆齿面方程。结合基蜗杆齿面与插齿刀齿面的包络条件,可得到基蜗杆齿面关于θs和φs双参数表达式为:
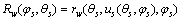 (9)
(9)
基蜗杆齿面经过坐标变换后,得到坐标系Sf中的基蜗杆齿面面族方程为:
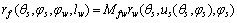 (10)
(10)
式中:Mfw为基蜗杆包络面齿轮的齐次变换矩阵;lw和φw为基蜗杆的包络运动参数。
基蜗杆包络面齿轮条件为:
 (11)
(11)
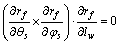 (12)
(12)
基蜗杆与面齿轮的瞬间接触点位置是由基蜗杆的转动参数φw和插齿刀轴线方向的运动参数lw决定的。联立式(10),(11)和(12),即得基蜗杆与面齿轮啮合接触点方程[10]。蜗杆头数nw=1,若蜗杆右旋,导程角λw=0.8°,面齿轮轴线与插齿刀轴线交角γ=90°,基蜗杆与面齿轮啮合的接触点如图8所示。
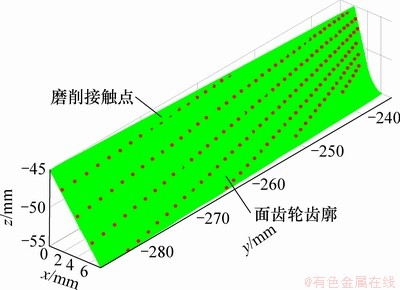
图8 基蜗杆与面齿轮啮合接触点
Fig. 8 Contact point between base worm and face-gear
4 光滑齿面面齿轮副最小油膜厚度
小齿轮和面齿轮之间的润滑为点接触润滑,它比线接触润滑问题复杂得多,发展缓慢[11]。Dowson和Higginson对各种载荷、速度和材料等参数下的弹流进行了广泛的数值计算,并在此基础上提出了符合实际使用情况的等温点接触弹流润滑的最小油膜厚度,点接触情况下的Dowson-Higginson最小膜厚公式为[12]:
 (13)
(13)
式中:Hmin为无量纲最小油膜厚度;U为速度参数;G为材料参数;W为载荷参数;k为椭圆参数。Hmin=hmin/Rx,hmin为最小油膜厚度;U=η0v/E′Rx,η0为动力黏度,v为齿面卷吸速度;G=α0E′;α0为润滑油黏压指数; ,F为法向接触力;k=1.03 (Ry/Rx)0.64,Rx=R1xR2x/(R1x+R2x),Ry=R1yR2y/(R1y+R2y),R1x,R1y和R2x,R2y为面齿轮在啮合点的主曲率半径,E′为综合弹性模量。
,F为法向接触力;k=1.03 (Ry/Rx)0.64,Rx=R1xR2x/(R1x+R2x),Ry=R1yR2y/(R1y+R2y),R1x,R1y和R2x,R2y为面齿轮在啮合点的主曲率半径,E′为综合弹性模量。
取动力黏度η0=0.075 N·s/m2,G=5 000,可得10点最小油膜厚度,面齿轮齿面沿齿顶向齿根方向啮合点最小油膜厚度的变化曲线如图9所示,面齿轮轮齿从进入啮合到脱离啮合过程中,最小油膜厚度逐渐增大,在齿根处出现最大值,小齿轮转角为0.25 rad时出现拐点,此时为啮合双齿变啮合单齿处。
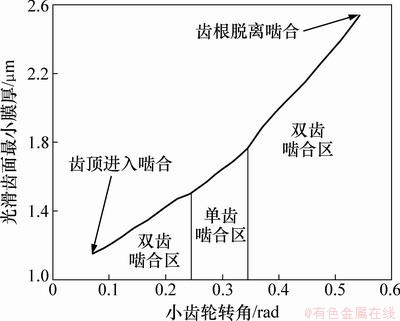
图9 面齿轮啮合过程中最小油膜厚度分布
Fig. 9 Distribution of minimum film thickness in meshing engagement
5 磨削后粗糙齿面最小油膜厚度
对面齿轮的磨削接触点和啮合点分别进行3次样条插值,得磨削接触轨迹和啮合轨迹如图10所示。面齿轮磨削齿面条纹方向与磨削轨迹方向一致,啮合轨迹为面齿轮传动时润滑油的流动方向。
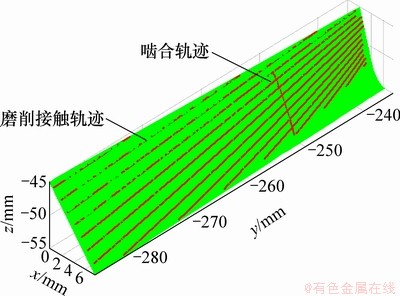
图10 磨削面齿轮表面方向图
Fig. 10 Grinding direction in face-gear
磨粒切削刃在砂轮表面呈随机分布状态,砂轮磨粒率为Vg,假设在砂轮内部任意切断的单位平面有Np颗磨粒,磨粒的平均直径为d,那么由1×d体积内磨粒数关系有[13]:
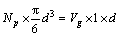 (14)
(14)
可得平均切削刃间隔为:
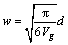 (15)
(15)
粒度号为M的磨粒平均直径d关系为[14]:
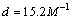 (16)
(16)
而磨粒率与砂轮组织号N关系为[15]:
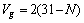 (17)
(17)
选取砂轮组织号N为6,M为100,结合式(15)和(16),得表面纹理示意图如图11所示,斜划线部分为磨削耕犁出的痕迹,旁边表面隆起形成一个高峰点,以面齿轮某个啮合点切线为y轴,x轴垂直于y轴,沿x轴和y轴分别取评定长度4 mm,求出2个方向高峰点个数,该点表面方向参数rc等于x和y方向高峰点数之比。
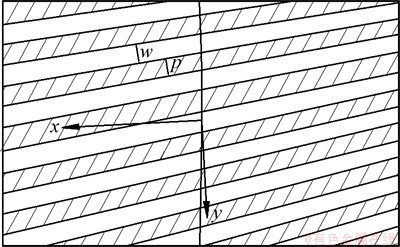
图11 齿面纹理示意图
Fig. 11 Sketch of texture in tooth surface
引入最小油膜厚度修正因子Cr,其为粗糙表面的最小润滑油膜厚度与不考虑表面形貌下的最小润滑子Cr的值[12]。膜厚比由下式求得:
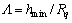 (18)
(18)
式中:Ra为综合粗糙度,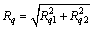 ,Ra1和Ra2为2个齿轮表面粗糙度均方根偏差。
,Ra1和Ra2为2个齿轮表面粗糙度均方根偏差。
对于服从随机高斯分布的粗糙表面,某齿轮的Rqi=1.25 Rai,设两齿轮粗糙度Ra相同,取值为0.6,0.4和0.2时,对应的膜厚比为Λ1,Λ2和Λ3,由插值法可求得10个啮合点不同表面方向参数与3种膜厚比下的最小油膜厚度修正因子Cr,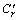 和
和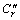 ,磨削面齿轮不同表面形貌的最小油膜厚度hmin1,hmin2和hmin3计算结果如表3所示。
,磨削面齿轮不同表面形貌的最小油膜厚度hmin1,hmin2和hmin3计算结果如表3所示。
图13所示为考虑表面方向参数,并且粗糙度为0.6,0.4和0.2时,磨削后面齿轮粗糙齿面从齿顶进入啮合到齿根退出啮合过程中最小油膜厚度随小齿轮转角的变化。
表3 不同表面形貌下最小油膜厚度计算结果
Table 3 Calculated value of minimum film thickness under different surface topographies
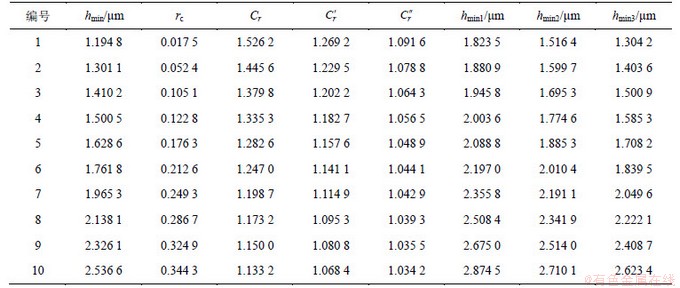
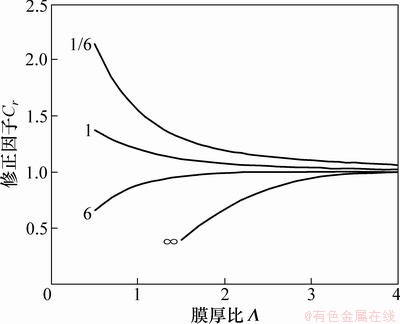
图12 粗糙表面对膜厚的影响
Fig. 12 Effects of rough surface on film thickness
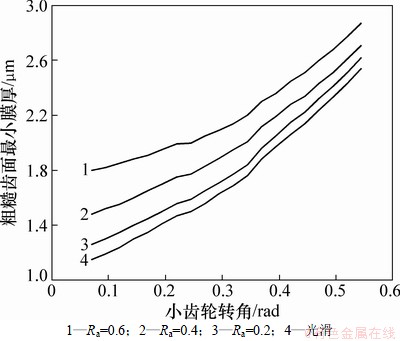
图13 粗糙齿面的最小油膜厚度
Fig. 13 Minimum film thicknesses of rough tooth surface
6 结论
(1) 随着啮合点由面齿轮齿顶向齿根移动,最小油膜厚度逐渐增大。计算的粗糙度范围内,增大粗糙度能够增大最小油膜厚度,但效果甚微,反而使润滑状态发生恶化,不利于齿轮的长期润滑使用寿命。
(2) 小齿轮转角为0.25 rad时,双齿啮合变单齿啮合,小齿轮转角为0.35 rad时,单齿啮合变双齿啮合,此两点接触力的急剧变化使油膜厚度变化曲线出现拐点。
(3) 磨削齿面形成的表面方向参数从面齿轮齿顶到齿根逐渐增大,在面齿轮靠近齿根处的啮合点有最大表面方向参数,不同粗糙度的情况下,靠近齿根的啮合点处最小油膜厚度较其他点变化最小。
参考文献:
[1] Litvin F L, Fuentes A, Handschuh R F, et a1. Face-gear drives with spur involute pinion:geometry generation by a worm, stress analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191(25/26): 2785-2813.
[2] Barone S, Borgianni L, Forte P. Evaluation of the effect of misalignment and profile modification in face gear drive by a finite element meshing simulation[J]. Journal of Mechanical Design, 2004, 126(5): 916-924.
[3] Amarnath M, Sujatha C, Swarnamani S. Expermental studies on the effects of reduction in gear tooth stiffness and lubricant film thickness in a spur geared system[J]. Tribology international, 2009, 42(2): 340-352
[4] Elcoate C D, Evans H P, Hughes T G, et al. Transient elastohydro-dynamic analysis of rough surface using a novel coupled differential deflection method[J]. Proceedings of the Institution of Mechanical Engineers, 2001, 215(4): 319-337.
[5] Snidle R W, Evans H P, Alanou M P, et al. Gearing tribology[C]//Dowson D. Proceedings of the 29th Leeds-Lyon Symposium on Tribology. Leeds, 2003: 575-588.
[6] 冯桂萍, 高创宽. 粗糙齿面啮合的热弹流润滑分析[J]. 太原理工大学学报, 2006, 37(1): 13-15.
FENG Guiping, GAO Chuangkuan. Thermal EHL analysis of rough teeth faces[J]. Journal of Taiyuan University of Technology, 2006, 37(1): 13-15.
[7] 畅通, 王优强. 考虑粗糙度的直齿圆柱齿轮热混合润滑分析[J]. 润滑与密封, 2009, 34(4): 35-39.
CHANG Tong, WANG Youqiang. Thermal mixed lubrication analyses of involute spur gear considering roughness[J]. Lubrication Engineering, 2009, 34(4): 35-39.
[8] 朱如鹏. 面齿轮传动的啮合特性研究[D]. 南京: 南京航空航天大学机电学院, 2000: 41-111.
ZHU Rupeng. Investigation on the meshing characteristics of face gear[D]. Nanjing: Nanjing University of Aeronautics and Astronautics. College of Mechanical and Electrical Engineering, 2000: 41-111.
[9] 李龙. 正交面齿轮传动的润滑分析[D]. 南京: 南京航空航天大学机电学院, 2007: 24-28.
LI Long. The analysis of elasto-hydrodynamics lubrication in face gear[D]. Nanjing: Nanjing University of Aeronautics and Astronautics. College of Mechanical and Electrical Engineering, 2007: 24-28.
[10] 高金忠. 面齿轮滚磨刀具设计与修整方法研究[D]. 南京: 南京航空航天大学机电学院, 2011: 20-30.
GAO Jingzhong. Research on structure design and dressing method of hobbing or grinding worm for manufacturing face gear[D]. Nanjing: Nanjing University of Aeronautics and Astronautics. College of Mechanical and Electrical Engineering, 2011: 20-30.
[11] 温诗铸, 黄平. 摩擦学原理[M]. 北京: 清华大学出版社, 2008: 66.
WENG Shizhu, HUANG Ping. Principles of tribology[M]. Beijing: Tsinghua University Press, 2008: 66.
[12] ZHU Dong, CHENG Shihua. Effect of surface roughness on the point contact EHL[J]. Tribology, 1988, 110(1): 32-37.
[13] 王德泉, 陈艳. 砂轮特性与磨削加工[M]. 北京: 中国标准出版社, 2001: 26.
WANG Dequan, CHEN Yan. Wheel characteristic and grinding machining[M]. Beijing: China Standard Press, 2001: 26.
[14] Syoji K. 磨削加工技术[M]. 郭隐彪, 王振忠, 译. 北京: 机械工业出版社, 2007: 22.
Syoji K. Grinding process technology[M]. GUO Yinbiao, WANG Zhenbiao, transl. Beijing: China Machine Press, 2001: 22.
[15] 许洪基, 陶燕光, 雷光. 齿轮手册[M]. 北京: 机械工业出版社, 2011: 171.
XU Hongji, TAO Yanguang, LEI guang. Gearing book[M]. Beijing: China Machine Press, 2011: 171.
(编辑 陈爱华)
收稿日期:2012-09-05;修回日期:2012-12-19
基金项目:国家重点基础研究发展计划(“973”计划)项目(2011CB706806)
通信作者:严宏志(1964-),男,湖南常德人,教授,从事高速高精数字制造理论与技术研究;电话:0731-88876612;E-mail:yhzcsu@163.com