DOI: 10.11817/j.issn.1672-7207.2018.04.008
基于Ease-off的螺旋锥齿轮齿面分区修形方法
严宏志1, 2,肖蒙1, 2,胡志安1, 2,艾伍轶1, 2,明兴祖3
(1. 中南大学 高性能复杂制造国家重点实验室,湖南 长沙,410083;
2. 中南大学 机电工程学院,湖南 长沙,410083;
3. 湖南工业大学 快速成型技术研究所,湖南 株洲,412007)
摘要:为预控双重螺旋法加工的螺旋锥齿轮的啮合性能,研究基于Ease-off的螺旋锥齿轮齿面修形方法。用大轮理论齿面展成得到小轮共轭齿面,基于预设的对称抛物线传动误差和接触迹,将齿面划分为小端、中间接触区、大端共3个区域,并基于局部共轭原理沿啮合线方向对3个区域进行3段抛物线修形,得到目标齿面;采用Ease-off齿面接触分析方法,对得到的目标齿面啮合性能进行分析。研究结果表明:传动误差的形状、幅值、接触迹线与接触印痕达到预置要求;分区修形方法为双重螺旋法加工的齿轮工作齿面、非工作齿面同步分区修形优化提供了新途径。
关键词:螺旋锥齿轮;Ease-off;分区修形;齿面接触
中图分类号:TH132.4 文献标志码:A 文章编号:1672-7207(2018)04-0824-07
A novel ease-off flank zoning modification method of spiral bevel gears
YAN Hongzhi1, 2, XIAO Meng1, 2, HU Zhian1, 2, AI Wuyi1, 2, MING Xingzu3
(1. State Key Laboratory for High Performance Complex Manufacturing,Central South University, Changsha 410083, China;
2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
3. Institution of Rapid Prototyping Technology, Hunan Industry University, Zhuzhou 412007, China)
Abstract: A novel ease-off flank zoning modification method was proposed to pro-control the meshing performance of spiral bevel gears manufactured by duplex helical method. The conjugate pinion tooth surface was modified to meet the preconditions, which was generated by gear theoretical tooth surface, and then the conjugate pinion tooth surface was divided into three regions, i.e., the toe, the middle and the heel. These regions’ modification with three segment parabolics were conducted along the contact path and the contact line. Ease-off tooth contact analysis methodology was used to analyze the target tooth surface meshing performance. The results show that the transmission error, contact path and contact line are the same as the pre-preconditions. The novel zoning modification method can be used for modification research of whole tooth surface of spiral bevel gears manufactured by duplex helical method.
Key words: spiral bevel gear; Ease-off; zoning modification; tooth contact
采用双重螺旋法加工齿轮具有高效、高速的特点,在一些发达国家普遍采用。采用双重螺旋法对加工齿轮齿面的优化设计具有重要意义。国内外研究者根据齿轮的啮合性能需求对齿面进行优化设计,如:ARGYRIS等[1-4]利用局部综合法预控参考点接触参数,实现了控制参考点附近的啮合性能,但无法对全齿面啮合性能进行控制;吴训成等[5]提出了齿面主动设计方法,通过预设传动误差和接触印痕进行齿面的一阶、二阶参数设计,但只针对单面法加工的齿面;田兴等[6]研究了少数齿非对称渐开线直齿轮的设计方法,通过此方法计算出达到最大重合度时的大、小轮最小齿数;Ease-off拓扑图反映了理论齿面偏离共轭齿面的程度,可直观反映出相配齿面的微观几何结构和啮合特性,苏进展等[7-11]提出基于Ease-off和敏感矩阵的弧齿锥齿轮优化设计方法,并对保证齿面的工作面的啮合性能进行了讨论;曹雪梅等[12-13]研究了满足高阶传动误差齿面拓扑结构设计方法,发现高阶传动误差计算齿面时常在齿根部分不收敛,且基于大轮齿面的预设接触轨迹并不能保证所求目标齿面接触迹线为直线的要求;杜进辅等[14]建立了对摆线齿准双曲面齿轮的主动设计方法,对双侧曲面采用类似的3段抛物线修形,其修形曲线不连续;王会良等[15]对斜齿轮齿面沿齿廓与齿向方向进行分段拓扑修形,将齿面划分为9个区域进行讨论,但根据齿廓与齿向进行齿面分区,不适用于螺旋锥齿轮。本文作者以实现双重螺旋法加工的全齿面分区修形优化为目标,以共轭齿面作为基准面,基于局部共轭原理,将齿面划分为3个区域,预设对称抛物线传动误差,对齿面进行沿啮合线方向的3段抛物线修形,得到1个符合要求的目标齿面,对工作齿面和非工作齿面进行算例验证。
1 完全共轭齿面
产形轮齿面与被加工齿轮的齿面是1对线接触完全共轭的齿面。将大轮齿面看作是产形轮齿面,小轮齿面看作是被加工齿面,即可以求解与大轮完全共轭的小轮齿面[12]。啮合坐标系见图1,其中,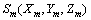 为固定坐标系,
为固定坐标系,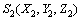 与大轮坐标系固联,
与大轮坐标系固联,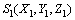 与小轮坐标系固联,Sf为辅助坐标系,E为偏置距,Σ为轴交角,φ1和φ2分别为小轮和大轮的啮合转角。
与小轮坐标系固联,Sf为辅助坐标系,E为偏置距,Σ为轴交角,φ1和φ2分别为小轮和大轮的啮合转角。
当小轮齿面与大轮齿面完全共轭时,大轮啮合转角φ2与小轮啮合转角φ1满足
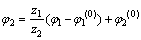 (1)
(1)
同时,两齿面啮合时啮合方程为
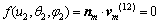 (2)
(2)
式中:φ1和φ2分别为小轮和大轮的啮合转角;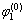 和
和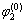 分别为小轮和大轮初始啮合角度;z1和z2分别为小轮和大轮齿数;
分别为小轮和大轮初始啮合角度;z1和z2分别为小轮和大轮齿数;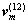 为相对速度。
为相对速度。
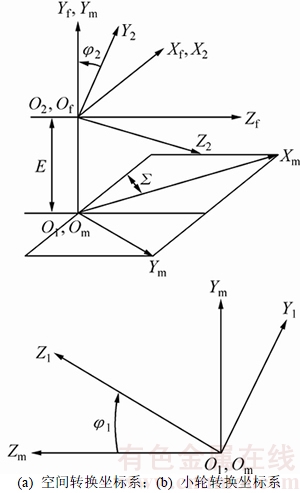
图1 啮合坐标系
Fig. 1 Mesh coordinate system
基于空间啮合理论和坐标变换,大轮齿面在坐标系S2中的位矢和法矢表达式为
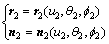 (3)
(3)
式中:u2和θ2为大轮刀具切削面的坐标参数;f2为加工大轮时的摇台转角。将大轮齿面看作产形轮齿面,小轮齿面看作被加工齿面,则与大轮齿面完全共轭的小轮齿面表达式为
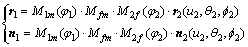 (4)
(4)
式中:Mij为坐标Si到坐标Sj的坐标变换矩阵。
2 满足预设啮合性能的齿面修形
2.1 预设的对称抛物线传动误差
由前面内容可以求出与大轮完全共轭的小轮齿面,但完全共轭的齿轮副对安装误差十分敏感,不具备可调性,因此,需要对完全共轭的齿面副进行修形,使齿轮副产生失配关系,变成局部共轭接触。
将传动误差曲线设计为抛物线,能够吸收由安装误差引起的线性误差,同时有利于降低振动和噪声[7],因此,本文预置传动误差曲线为开口向下左右对称的抛物线,如图2所示。图2中:横坐标φ1为小轮转角;纵坐标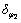 为传动误差;φ1L,φ1M和φ1N分别为啮入点L、参考点M和啮出点N的小轮转角;δT1为啮合转换点的传动误差;z1为小轮齿数;2π/z1为小轮单个啮合周期转角。
为传动误差;φ1L,φ1M和φ1N分别为啮入点L、参考点M和啮出点N的小轮转角;δT1为啮合转换点的传动误差;z1为小轮齿数;2π/z1为小轮单个啮合周期转角。
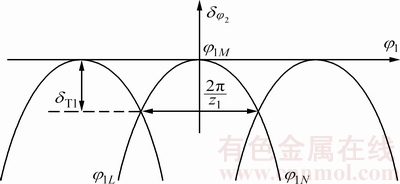
图2 对称抛物线形传动误差曲线
Fig. 2 Transmission error curve of symmetric parabolic
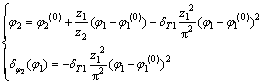 (5)
(5)
式中:φ2为大轮转角;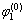 和
和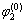 为2轮初始啮合位置;
为2轮初始啮合位置;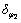 (φ1)为预置的抛物线形传动误差曲线函数;z2为大轮齿数。
(φ1)为预置的抛物线形传动误差曲线函数;z2为大轮齿数。
单独满足传动误差的共轭小轮齿面不能达到良好的啮合性能[13],需要对小轮继续进行基于预设接触迹及沿啮合线方向的修形。
2.2 预设的接触迹
接触迹线的形状、大小及位置直接影响齿轮副的运动、润滑特性以及传动效率和承载能力[14]。
将接触迹线设计为直线可以减小齿面对安装误差的敏感性。在大轮完全共轭齿面上预设接触迹线,如图3所示(其中,β为接触迹线与节锥线的夹角,α为瞬时接触椭圆长半轴)。
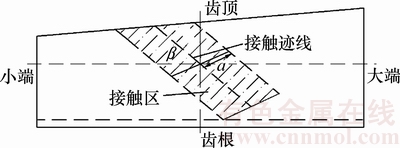
图3 接触迹线示意图
Fig. 3 Schematic diagram of contact line
2.3 齿面的网格划分
为确定齿面数据,需要对齿面进行离散化处理,在齿轮投影面上划分网格。在全齿面上沿齿长方向取m个点,沿齿高方向取n个点[16](如图4所示),计算投影面内网格点的坐标。图4中,O为设计交叉点,Zp为交叉点到节锥顶点的距离,Am为节锥顶点与M点的距离,δm为节锥角。
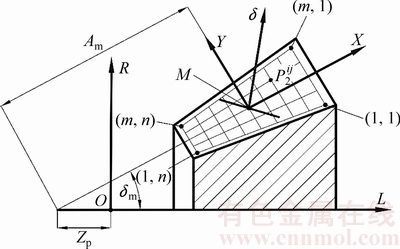
图4 齿面网格划分
Fig. 4 Mesh of tooth surface
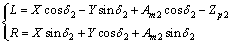 (6)
(6)
齿面上任一网格点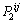 与大轮投影面内数据点满足方程[17]:
与大轮投影面内数据点满足方程[17]:
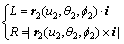 (7)
(7)
式中:i为在对应坐标系中大轮的旋转轴。
在O-LR坐标系中,设定的接触迹线满足方程:
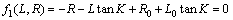 (8)
(8)
式中:L0和R0为参考点处的坐标;K为接触迹线方向角。
3 齿面分区修形
图5所示为齿面分区修形的示意图。将齿面分成小端、中间接触区和大端3部分,保证齿面连续可导。沿啮合线方向进行3段抛物线修形,小端、中间接触区和大端分别对应1段抛物线。
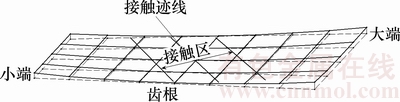
图5 齿面分区示意图
Fig. 5 Partition diagram of tooth surface
以啮合线与接触迹线的交点为坐标原点,齿面法线方向为y,指向轮齿大端的椭圆长轴方向为x方向,建立如图6所示的坐标系,修形曲线见图7。
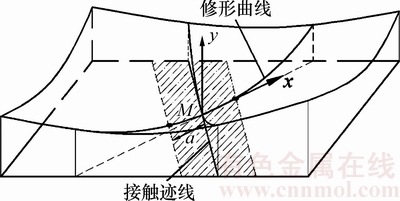
图6 多段抛物线修形示意图
Fig. 6 Schematic diagram of polyline modification curves
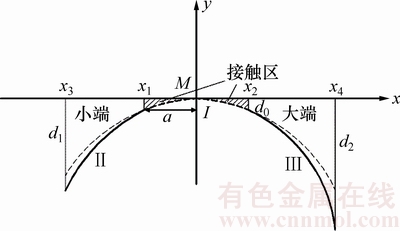
图7 修形曲线
Fig. 7 Modification curves
在设计接触区内,沿啮合线方向按照抛物线Ⅰ进行修形。在小端区域内,沿啮合线方向按照抛物线Ⅱ进行修形。在大端区域内,沿啮合线方向按照抛物线Ⅲ进行修形。啮合区外的修形量可以根据实际工况情况进行确定。
啮合线方向修形曲线方程表达式为
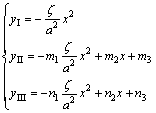 (9)
(9)
式中:a为预置的瞬时接触椭圆长半轴的长度;ζ为接触齿面间的弹性变形量[18],一般取ζ=0.00 635 mm。
要保证整个齿面连续可导,应该满足以下几个约束条件:
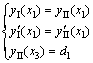 (10)
(10)
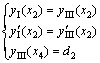 (11)
(11)
式中:x1和x2均等于预设的接触椭圆长半轴长度a;x3和x4分别为靠小端和大端齿面区域内沿x轴到接触迹线的最远距离;d1和d2分别为小端、大端的最大修形量。
则沿啮合线方向的法向修形量如下。
当-a≤x≤a时,
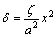 (12)
(12)
当-x3≤x<-a时,
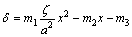 (13)
(13)
当a≤x<x4时,
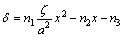 (14)
(14)
4 算例
以1对大轮采用成形法、小轮采用双重螺旋法加工的准双曲面齿轮副的工作面为例[19],大、小轮的基本参数见表1,大轮加工参数见表2,分区修形预设参数见表3。
图8和图9所示分别为满足对称抛物线修形的小轮凹凸两面差曲面的失配拓扑结构图。从图8和图9可以看出:对称抛物线传动误差对小轮齿面进行了内对角修形,小轮工作面大端修形量大于小端修形量,小轮非工作面小端修形量大于大端修形量。小轮齿面与大轮齿面为线接触,由于满足对称抛物线传动误差,齿面沿接触线方向产生了修正量。
将齿面分成小端、中间接触区和大端3部分,沿啮合线方向对3个区域进行对应的抛物线修形。图10~13所示分别为工作面、非工作面分区修形曲线及沿啮合线方向分区修形曲线,其中,图10和图12所示分别为工作面和非工作面的分区修形曲线;图11和图13所示分别为按照修形曲线沿啮合线修形后的齿面失配拓扑图。从图10~13可以看出:齿面沿啮合方向产生了修正量;小端和大端的最大修形量与预设值一致,齿面在外对角方向产生了修形。
表1 基本参数
Table 1 Basic parameters
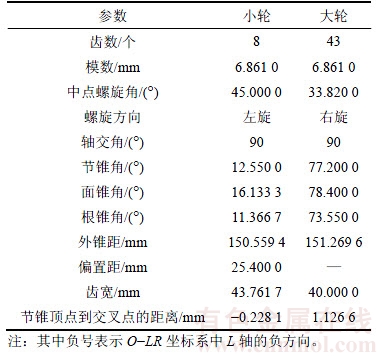
表2 大轮加工参数
Table 2 Process parameters of gear
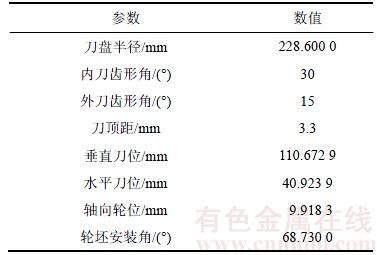
表3 预设参数
Table 3 Preset parameters
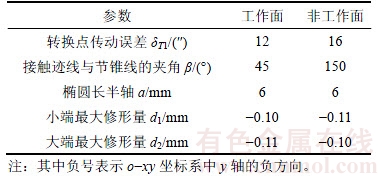
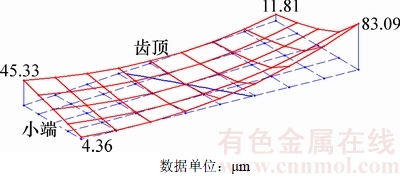
图8 满足对称抛物线传动误差的工作齿面
Fig. 8 Drive side based on symmetric parabolic transmission error
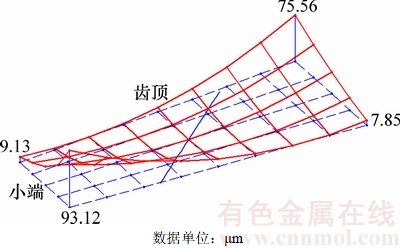
图9 满足对称抛物线传动误差的非工作齿面
Fig. 9 Coast side based on symmetric parabolic transmission error
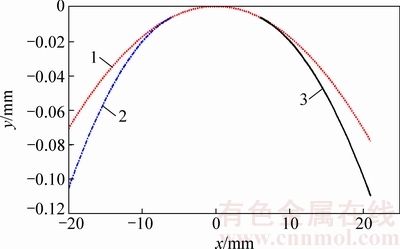
图10 工作面分区修形曲线
Fig. 10 Zoning modification curves of drive side
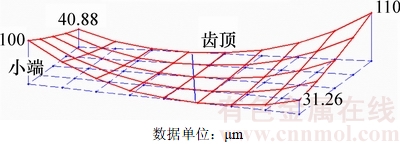
图11 工作面沿啮合线方向分区修形
Fig. 11 Drive side of zoning modification along contact line
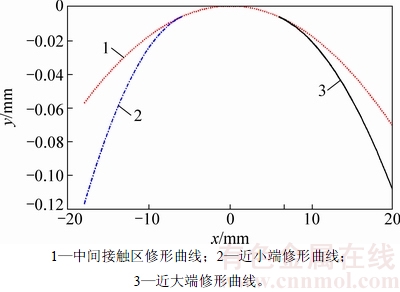
图12 非工作面分区修形曲线
Fig. 12 Zoning modification curves of coast side
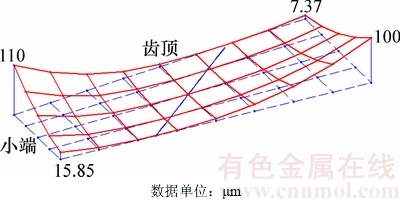
图13 非工作面沿啮合线方向分区修形
Fig. 13 Coast side of zoning modification along contact line
齿面经过对称抛物线修形及沿啮合线方向的分区修形后,产生满足预设要求的目标齿面,如图14和图15所示。从图14和图15可以看出:最终目标齿面齿面与大轮齿面为点接触,不仅沿接触迹线产生修正量,而且沿啮合线产生了修正量。
运用Ease-off齿面接触分析方法对得到的目标齿面进行啮合性能验证,可以得到目标齿面的接触区和传动误差曲线,如图16~19所示。
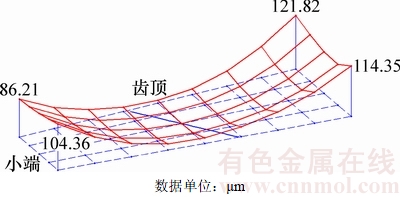
图14 最终工作齿面
Fig. 14 The final drive side

图15 最终非工作齿面
Fig. 15 The final coast side

图16 小轮工作面接触印痕
Fig. 16 Contact pattern of drive side
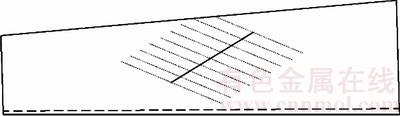
图17 小轮非工作面接触印痕
Fig. 17 Contact pattern of coast side
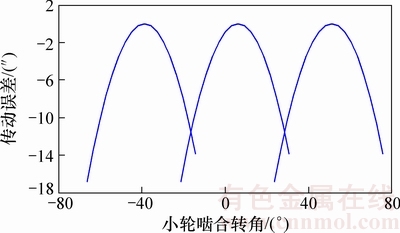
图18 小轮工作面传动误差曲线
Fig. 18 Transmission error of drive side
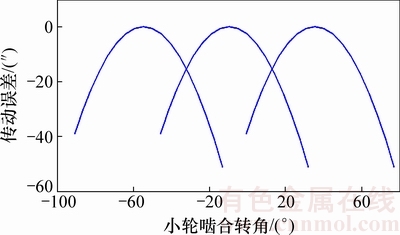
图19 小轮非工作面传动误差曲线
Fig. 19 Transmission errors of coast side
由图16~19可知:用大轮理论齿面展成得到了小轮共轭齿面并经过预设传动误差、接触迹线和沿啮合线方向的分区修形,得到的目标齿面的接触区、传动误差值与预置值基本相符;接触印痕位于齿面中部区域,接触区未发生畸变,工作面的传动误差转换点为12″,非工作面的传动误差转换点为15″,满足预置啮合性能的要求。
5 结论
1) 针对双重螺旋法加工的凹凸两面修形,用大轮理论齿面展成得到小轮共轭齿面,并进行满足预置传动误差、预置接触迹和齿面分区修形,得到合理的目标齿面的齿面设计方法,为齿面的修正和修形研究提供了参考。
2) 采用对称抛物线传动误差预置,将齿面划分为大端、小端和中间接触区共3个区域,并通过三段抛物线修形,在沿啮合线方向上产生了预设的修形量,从而得到了满足预设要求的目标齿面,实现了对满足预置啮合性能的理想齿面的控制,可为全齿面的分区优化研究提供参考。
参考文献:
[1] ARGYRIS J, FUENTES A, LITVIN F L. Computerized integrated approach for design and stress analysis of spiral bevel gears[J]. Computer Methods in Applied Mechanics & Engineering, 2002, 191(11/12): 1057-1095.
[2] LITVIN F L, WANG A G, HANDSCHUH R F. Computerized generation and simulation of meshing and contact of spiral bevel gears with improved geometry[J]. Computer Methods in Applied Mechanics & Engineering, 1998, 158(1/2): 35-64.
[3] LITVIN F L, FUENTES A, QI Fan, et al. Computerized design, simulation of meshing, and contact and stress analysis of face-milled formate generated spiral bevel gears[J]. Mechanism and Machine Theory, 2002, 37(5): 441-459.
[4] LITVIN F L, FUENTES A, HAYASAKA K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears[J]. Mechanism and Machine Theory, 2006, 41(1): 83-118.
[5] 吴训成, 毛世民, 吴序堂. 点啮合齿面主动设计研究[J]. 机械工程学报, 2000, 36(4): 70-72.
WU Xuncheng, MAO Shiming, WU Xutang. On function-oriented design of point contact surfaces[J]. Journal of Mechanical Engineering, 2000, 36(4): 70-72.
[6] 田兴, 李威. 基于少齿数的非对称渐开线齿轮主动设计[J]. 中南大学学报(自然科学版), 2013, 44(3): 955-962.
TIAN Xing, LI Wei. Direct design for asymmetric involute gear base on small teeth[J]. Journal of Central South University (Science and Technology), 2013, 44(3): 955-962.
[7] 苏进展, 贺朝霞. 弧齿锥齿轮齿面的高精度修形方法[J]. 华南理工大学学报(自然科学版), 2014, 42(4): 91-96.
SU Jinzhan, HE Zhaoxia. High-precision modification of tooth surface for spiral bevel gears[J]. Journal of South China University of Technology (Natural Science Edition), 2014, 42(4): 91-96.
[8] 苏进展, 方宗德. 弧齿锥齿轮低敏感性修形[J]. 航空动力学报, 2012, 27(8): 1895-1901.
SU Jinzhan, FANG Zongde. Low sensitivity modification for spiral bevel gears[J]. Journal of Aerospace Power, 2012, 27(8): 1895-1901.
[9] SHIH Y P. A novel ease-off flank modification methodology for spiral bevel and hypoid gears[J]. Mechanism and Machine Theory, 2010, 45(8): 1108-1124.
[10] ARTONI A, KOLIVAND M, KAHRAMAN A. An ease-off based optimization of the loaded transmission error of hypoid gears[J]. Journal of Mechanical Design, 2010, 132(1): 011010.
[11] ARTONI A, GABICCINI M, KOLIVAND M. Ease-off based compensation of tooth surface deviations for spiral bevel and hypoid gears: only the pinion needs corrections[J]. Mechanism and Machine Theory, 2013, 61(1): 84-101.
[12] 曹雪梅, 方宗德, 张金良, 等. 弧齿锥齿轮的齿面主动设计[J]. 机械工程学报, 2007, 43(8): 155-158.
CAO Xuemei, FANG Zongde, ZHANG Jinliang, et al. Function- oriented active tooth surface design of spiral bevel gears[J]. Journal of Mechanical Engineering, 2007, 43(8): 155-158.
[13] 曹雪梅, 邓效忠, 聂少武. 基于共轭齿面修正的航空弧齿锥齿轮高阶传动误差齿面拓扑结构设计[J]. 航空动力学报, 2015, 30(1): 195-200.
CAO Xuemei, DENG Xiaozhong, NIE Shaowu. Ease-off flank topography design for aviation spiral bevel with higher-order transmission errors by modification of conjugate flank[J]. Journal of Aerospace Power, 2015, 30(1): 195-200.
[14] 杜进辅, 方宗德, 张永振, 等. 摆线齿准双曲面齿轮齿面主动设计[J]. 国防科技大学学报, 2015, 37(6): 167-174.
DU Jinfu, FANG Zongde, ZHANG Yongzhen, et al. Active tooth surface design of cycloid hypoid gears[J]. Journal of National University of Defense Technology, 2015, 37(6): 167-174.
[15] 王会良, 邓效忠, 徐恺, 等. 考虑安装误差的拓扑修形斜齿轮承载接触分析[J]. 西北工业大学学报, 2014, 32(5): 781-786.
WANG Huiliang, DENG Xiaozhong, XU Gai, et al. Consider installation error topological modification of helical gear bearing and contact analysis[J]. Journal of Northwestern Polytechnical University, 2014, 32(5): 781-786.
[16] 唐进元, 聂金安, 王智泉. 螺旋锥齿轮HFT法加工的反调修正方法[J]. 中南大学学报(自然科学版), 2012, 43(6): 2142-2149.
TANG Jinyuan, NIE Jinan, WANG Zhiquan. Reverse correction of spiral bevel gear HFT method[J]. Journal of Central South University (Science and Technology), 2012, 43(6): 2142-2149.
[17] 聂少武. 基于完全共轭的摆线锥齿轮齿面失配设计及修正理论研究[D]. 西安: 西北工业大学机电学院, 2015: 55-56.
NIE Shaowu. Study on tooth flank mismatch design and modification theory based on fully conjugated cycloid bevel gears[D]. Xi’an: Northwestern Polytechnical University. School of Mechanical Engineering, 2015: 55-56.
[18] 曾韬. 弧齿锥齿轮设计与加工[M]. 哈尔滨: 哈尔滨工业大学出版社, 1989: 248-251.
ZENG Tao. Design and manufacture of spiral bevel and hypoid gears[M]. Harbin: Harbin Institute of Technology Press, 1989: 248-251.
[19] 张宇, 严宏志, 曾韬. 弧齿锥齿轮双重螺旋法切齿原理及齿面接触分析研究[J]. 机械工程学报, 2015, 51(21): 15-23.
ZHANG Yu, YAN Hongzhi, ZENG Tao. Cutting principle and tooth contact analysis of spiral bevel and hypoid gears generated by duplex helical method[J]. Journal of Mechanical Engineering, 2015, 51(21): 15-23.
(编辑 陈灿华)
收稿日期:2017-05-10;修回日期:2017-07-22
基金项目(Foundation item):国家自然科学基金资助项目(51575533, 51375161)(Projects(51575533, 51375161) supported by the Natural National Science Foundation of China)
通信作者:严宏志,博士,教授,从事复杂曲面数字制造理论与技术研究;E-mail:yhzcsu@163.com