文章编号：1004-0609(2013)S1-s0231-05

高速变形过程中工业纯钛的孪生强化效应

邓希光，惠松骁，叶文君，付艳艳

(北京有色金属研究总院 有色金属材料制备加工国家重点实验室，北京 100088)

摘  要：对工业纯钛Gr2的准静态(1×10^-3 s^-1)和动态(3×10³ s^-1和6×10³ s^-1)力学性能曲线进行测量，并通过等温变形曲线计算材料压缩变形时的应变硬化模量。结果表明：塑性应变低于0.2时，动态变形过程的应变硬化模量明显高于准静态变形过程的。通过孪生分数统计和变形组织观察发现，应变速率提高对应变硬化的强化效应源自于塑性变形初期(ε_p≤0.2)孪晶的大量形成，即孪生强化效应。然而，随着变形的持续进行，孪生强化效应会随着组织中二次孪晶的形成和位错切过孪晶界导致的晶界扭曲而逐渐减弱并消失。位错运动至孪晶界时，受到的阻力以及塞积和切过行为将是影响孪生强化效应的主要因素。

关键词：纯钛；孪生；高应变速率；应变硬化；临界分切应力

中图分类号：TG146.2　　     文献标志码：A

Twinning strength effect of CP titanium during high-strain-rate deformation

DENG Xi-guang, HUI Song-xiao, YE Wen-jun, FU Yan-yan

(State Key Laboratory of Non-ferrous Metals and Processing, General Research Institute for Non-ferrous Metals, Beijing 100088, China)

Abstract: The quasi-static (1×10^-3 s^-1) and dynamic (3×10³ s^-1 and 6×10³ s^-1) mechanical properties curves of commercial pure (CP) titanium Gr2 were obtained, and the strain hardening modulus was derived based on isothermal compression curves. The results show that within plastic strain of 0.2, the strain hardening modulus of dynamic deformation process is evidently higher than that of quasi-static process. The twin fraction measurement and microscopic observation of the deformed structure show that the enhancement of strain hardening in the dynamic process is closely related with the abundance of mechanical twinning. As the material deforms further, second order twinning forms, and twin boundary is distorted by dislocation, which leads to the fact that the twinning strengthen effect becomes weaker, and finally disappears. The interaction between dislocation and twin boundary is the influencing factor of the twinning strength effect.

Key words: pure titanium; twinning; high-strain-rate; strain hardening; critical shear stress

具有HCP结构的α-Ti及其合金具有比强度高，耐腐蚀性能好及综合力学性能优良等诸多优点，因而被广泛应用于航空航天、船舶及兵器工业等领域^[1]。但是该类材料在强冲击作用下进行高应变速率塑性变形时的绝热剪切敏感性较大，容易形成动态裂纹并导致破坏^[2]。众多研究人员从材料的宏观参数特性的角度分析，认为其主要原因如下：1) 塑性变形时的流变应力水平会随着随温度升高显著下降；2) 塑性变形时的应变硬化效果较差；3) 钛本身的热导率较低^[3]。其中，α-Ti的宏观应变硬化行为主要取决于两种微观塑性变形机制以及滑移和孪生之间的相互作用与协调^[4]。因此，塑性变形过程中的环境温度和应变速率会通过影响滑移和孪生行为改变α-Ti的宏观力学性能。

孙巧艳等^[5]通过测量工业纯钛在液氮中(-196 ℃)准静态变形时的屈服强度以及统计塑性变形各阶段的孪晶分数，发现变形温度的降低会显著提高材料的屈服强度，并在均匀塑性变形的初期阶段(ε_p=5.8%)使50%的晶粒发生孪生变形。若将此实验结果与SALEM等^[6]提出“HCP钛中变形孪晶的增殖能够提高应变硬化速率”的结论相结合，可以合理地推测低温下纯钛塑性变形初期阶段的应变硬化率会因变形孪晶的大量形成而提高。此推论预示着应变速率的提高也将影响纯钛变形组织的孪生行为，并改变材料的应变硬化效应，这是因为变形温度的降低和应变速率的提高都会使位错运动的阻力增大，从而使材料的宏观力学性能向着相同的方向变化^[7]。

DENG等^[8]在对工业纯钛准静态和动态变形组织中的孪生类型进行标定并结合应力状态进行统计分析后发现，孪生系的开动需要满足特定应力条件，且应变速率对其临界分切应力值无显著影响。因此，与准静态变形相对比，应变速率提高导致流变应力增大会改变组织中的孪晶分数和材料应变硬化行为。本文作者通过对比工业纯钛的动态和准静态应力应变曲线，统计变形过程中孪晶分数，由此探讨应变速率提高对孪生组织特征和宏观力学性能的影响，并对作用机制进行分析。

1  实验

本研究使用的材料是由宝鸡钛业根据ASTM标准B348-10生产的工业纯钛Gr2热轧棒材，其直径为30 mm。原始组织为晶粒尺寸30 μm的等轴组织，并含有少量退火孪晶。压缩变形试样为d5 mm×5 mm圆柱，加工轴向与原始棒材轴向平行。

室温下应变速率为1×10^-3 s^-1的准静态等温压缩在MTS万能试验机上进行。动态压缩在分离式霍普金森压杆(SHPB)上进行。为了消除试样高速变形时绝热温升引起的热软化效应，从而得到室温下动态变形过程的等温应力—应变曲线，在本研究中，采用对同一试样重复加载并逐步增大变形量的方法。每次加载间隔10 min，以便试样温度恢复至室温。由于SHPB无法像万能试验机一样压缩试样至特定变形量并卸载，因此，需要采用不同高度的限位环逐步控制动态变形量。

对变形组织进行观察前先将试样垂直于轴向切开，剖面采用砂纸逐级打磨至5000^#后在5%HClO₄+ 95% CH₃COOH(体积分数)溶液中电解抛光，然后由5%HF+15%HNO₃+80%H₂O(体积分数)溶液腐蚀出晶界。金相观察在Zeiss Axiovert 200 Mat光学显微镜上进行，孪晶形貌观察在JSM-7001F扫描电子显微镜上进行。

2  结果与分析

2.1       准静态及动态力学性能

图1所示为试样在4种不同变形条件下的真应力—塑性真应变关系曲线。其中由虚线1~4是对同一样品进行4次重复SHPB加载得到的曲线，其应变速率均约为3 000 s^-1。通过逐步降低限位环的高度，将每次变形的塑性应变控制在0.1左右。根据材料在绝热状态下的变形温升公式△T=β∫σ(ε)dε/(ρc)^[9]，可知每次加载的温升不超过50 ℃，而且加载间隔阶段的冷却过程可以恢复样品温度至室温。因此，绝热温升导致的材料热软化效应可忽略不计。若将前次加载后的终止状态视为下次加载的起始状态，可将曲线1~4按照加载顺序和变形量依次组合，再根据幂函数形式的Hollomon方程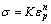拟合得到曲线5，并将其视为试样在室温下以3 000 s^-1变形时的等温应力—应变曲线。曲线6~7均为SHPB单次加载得到的曲线，其应变速率分别为3 000 s^-1和6 000 s^-1，变形后期的绝热温升可高达200 ℃，因此，将其视为绝热变形过程。除上述7组动态性能外，曲线8为万能试验机准静态压缩测得的应变速率1×10^-3 s^-1等温应力—应变曲线。

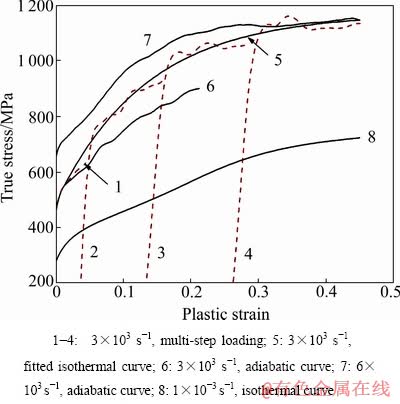
图1  试样的动态及准静态应力—应变曲线

Fig. 1  Dynamic and quasi-static stress—strain curves of samples

在这些曲线中只有等温变形曲线5和8不受绝热温升的热软化作用的影响，因此，相差3×10⁶倍的应变速率是导致其间差别的唯一因素。若关于塑性应变求解真应力的一阶导数可得到应变硬化模量，如图2所示，以此对比动态和准静态变形过程之间的应变硬化效应。当塑性应变低于0.2时，动态变形过程的应变硬化模量dσ/dε明显高于准静态变形过程，这说明在塑性变形前期，应变速率的提高能够强化纯钛的应变硬化效应。为探究产生此强化效应的原因，需对塑性变形各阶段的组织形貌进行显微观察。

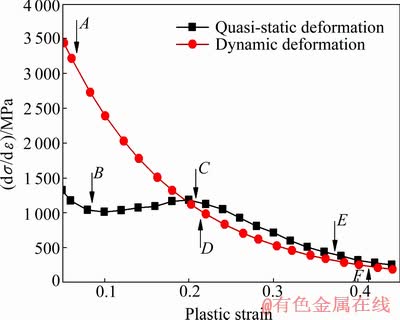
图2  动态及准静态塑性变形过程中工业纯钛Gr2应变硬化模量的变化曲线

Fig. 2  Strain hardening modulus curves of CP Ti Gr2 during dynamic and quasi-static deformation process

2.2  准静态及动态变形的孪晶形貌和分数变化

对图2中A和B点对应的变形样品进行光学显微观察，金相组织如图3所示，其中动态变形孪晶较窄，孪晶界平直，而且一个晶粒内部经常出现多个孪晶，这说明提高变形速率能够促进孪晶的形核，但是由于变形时间短，孪晶长大不明显。

为了定量反映变形过程中孪生晶粒数量的变化趋势，对同一样品不同视场的5幅金相照片进行测量，统计出特定塑性应变样品中孪晶分数的平均值、最大值和最小值，以此绘制孪晶分数曲线如图6所示。图中塑性应变小于0.1数据点的误差较大，原因在于此时单个晶粒中的孪晶数量较少，使得孪生晶粒和未发生孪生的晶粒间的晶界比较模糊，给测量带来一定困难。即便如此，统计结果还是能够比较准确地反映出孪晶分数的变化趋势。

图3  图2中A和B对应样品的变形组织的金相组织

Fig. 3  Metallographs of deformed structure corresponding to points A and B shown in Fig. 2

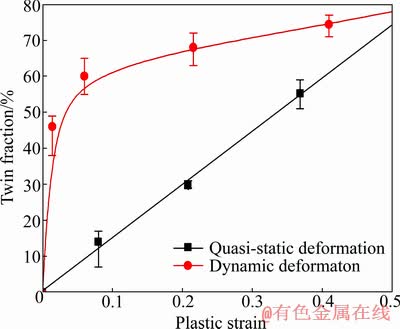
图4  Gr2工业纯钛在准静态和动态压缩过程中的孪晶分数

Fig. 4  Twin fraction of Gr2 CP Ti during dynamic and quasi-static compression processes

图4中对于未发生变形的样品，认为其孪晶分数为0，并将该状态作为曲线的起始点(坐标原点)。在准静态变形过程中，样品中发生孪生变形的晶粒数量随着宏观变形量的增大成线性趋势增多。然而对于动态变形过程，孪晶分数在0~0.1应变范围内急剧增加，随之以较平缓的速度逐渐增大，直至趋于饱和，该趋势与纯钛在低温-196 ℃拉伸变形时的孪晶分数演化规律基本一致^[7]。从整体来看，动态变形时孪生晶粒的体积分数高于准静态变形，尤其在0~0.2应变范围内，这说明提高应变速率对孪晶分数的影响主要发生在塑性变形的初期阶段，然而，当材料进一步变形至0.5时，两种应变速率下的孪晶分数均为75%左右。对比图2和4中应变0~0.2范围的数据可知，动态变形时，孪晶分数的急剧增加是导致其应变硬化模量较高的主要原因。此时孪晶的显微形貌如图5中的(a)和(b)所示，分别对应图2中的C和D指示的应变，此时孪晶界面较平直。当变形至图4中的E和F位置时，孪晶形貌如图5中的(c)和(d)所示，孪晶界发生扭曲并伴有二次孪晶的形成，而且动态变形组织(图5(d))中的孪晶扭曲更为严重，原始晶界已难以识别。这说明大量位错通过孪晶界改变了孪晶形貌，其形态的改变会影响孪生组织对材料的强化效果。图2中两条曲线在0.2~0.5范围内几乎重合，说明此时的孪生强化效应已经消失。

宏观应变速率的提高对应着微观位错运动速度的加快，其理论极限值为材料中弹性剪切波的传播速度^[10]。由于位错滑移时受到的晶格阻力与运动速度成正比，因此，与准静态相比动态塑性变形时材料内部的应力水平会因位错运动阻力的升高而增大。然而，应变速率提高对孪生的临界分切应力值并无显著影响，所以，在单向压应力作用下动态变形组织中将有更多的晶粒发生孪生变形，而且单个晶粒内的孪晶数量也较多。由此引入的大量孪晶界在塑性变形初期(ε_p≤0.2)会强化纯钛的应变硬化效应，即孪生强化效应。随着纯钛的继续变形，孪生强化效应会随着二次孪晶的形成和位错切过孪晶界导致的晶界扭曲而逐渐减弱并消失。由此可见，纯钛中不同类型的位错运动至不同类型孪晶界时的受到的阻力以及塞积和切过行为将是影响孪生强化效应的主要因素。

3  结论

1) 利用分离式霍普金森压杆加限位环的实验方法能够实现对压缩样品的多重加载，并拟合出材料在高应变速率下的等温变形曲线。

2) 塑性应变低于0.2时，动态变形过程的应变硬化模量明显高于准静态变形过程。应变速率提高对应变硬化的强化效应源自于塑性变形初期孪晶的大量形成。

3) 塑性应变高于0.2时，孪生强化效应会随着组织中二次孪晶的形成和位错切过孪晶界导致的晶界扭曲而逐渐减弱并消失。

图5  孪晶形组织的SEM像

Fig. 5  SEM images of deformed twin structure

REFERENCES

[1] LüTJERING G, WILLIAMS J C. Titanium [M]. Verlag Berlin Heidelberg: Springer, 2007.

[2] MURR L, RAMIREZ A, GAYTAN S. Microstructure evolution associated with adiabatic shear bands and shear band failure in ballistic plug formation in Ti-6Al-4V targets [J]. Materials Science and Engineering A, 2009, 516(1/2): 205-216.

[3] LIAO S C, DUFFY J. Adiabatic shear bands in a TI-6Al-4V titanium alloy [J]. Journal of the Mechanics and Physics of Solids, 1998, 46(11): 2201-2231.

[4] YOO M. Slip, twinning and fracture in hexagonal close-packed metals [J]. Metallurgical and Materials Transactions A, 1981, 12(3): 409-418.

[5] 孙巧艳, 朱蕊花, 刘翠萍, 于振涛. 工业纯钛机械孪晶演化及其对纯钛低温力学性能的影响[J]. 中国有色金属学报, 2006, 16(4): 592-598.

SUN Qiao-yan, ZHU Rui-hua, LIU Cui-ping, YU Zhen-tao. Twinning behavior and its effect on mechanical behavior of commercial titanium at cryogenic temperature [J]. The Chinese Journal of Nonferrous Metals, 2006, 16(4): 592-598.

[6] SALEM A A, KALIDINDI S R, DOHERTY R D. Strain hardening of titanium: Role of deformation twinning [J]. Acta Materialia, 2003, 51(14): 4225-4237.

[7] GRAY III G T. Influence of strain rate and temperature on the structure: Property behavior of high-purity titanium [J]. Le Journal de Physique IV, 1997, 7(C3): 423-428.

[8] DENG X G, HUI S X, YE W J, SONG X Y. Analysis of twinning behavior of pure Ti compressed at different strain rates by Schmid factor [J]. Materials Science and Engineering A, 2013, 575: 15-20.

[9] HODOWANY J, RAVICHANDRAN G, ROSAKIS A, ROSAKIS P. Partition of plastic work into heat and stored energy in metals [J]. Experimental Mechanics, 2000, 40(2): 113-1230

[10] PEIRS J, TIRRY W, AMIN-AHMADI B, et al. Microstructure of adiabatic shear bands in Ti6Al4V [J]. Materials Characterization, 2013, 75: 79-92.

(编辑  李艳红)

收稿日期：2013-07-28；修订日期：2013-10-10

通信作者：惠松骁，教授，博士；电话：010-82241172；E-mail: huisx@grinm.com