J. Cent. South Univ. (2017) 24: 2121-2133

DOI: https://doi.org/10.1007/s11771-017-3621-7

Visualization of pullout behaviour of geogrid in sand with emphasis on size effect of protrusive junctions

MIAO Chen-xi(苗晨曦)¹, ZHENG Jun-jie(郑俊杰)¹, ZHANG Rong-jun(章荣军)¹,

XIE Ming-xing(谢明星)¹, YIN Jian-hua(殷建华)²

1. Institute of Geotechnical and Underground Engineering, Huazhong University of Science and Technology,Wuhan 430074, China;

2. Department of Civil and Environmental Engineering, The Hong Kong Polytechnic University, Hung Hom,Kowloon, Hong Kong, China

Central South University Press and Springer-Verlag GmbH Germany 2017

Abstract: Geogrid has been extensively used in geotechnical engineering practice due to its effectiveness and economy. Deep insight into the interaction between the backfill soil and the geogrid is of great importance for proper design and construction of geogrid reinforced earth structures. Based on the calibrated model of sand and geogrid, a series of numerical pullout tests are conducted using PFC^3D under special considerations of particle angularity and aperture geometry of the geogrid. In this work, interface characteristics regarding the displacement and contact force developed among particles and the deformation and force distribution along the geogrid are all visualized with PFC^3D simulations so that new understanding on how geogrid-soil interaction develops under pullout loads can be obtained. Meanwhile, a new variable named fabric anisotropy coefficient is introduced to evaluate the inherent relationship between macroscopic strength and microscopic fabric anisotropy. A correlation analysis is adopted to compare the accuracy between the newly-proposed coefficient and the most commonly used one. Furthermore, additional pullout tests on geogrid with four different joint protrusion heights have been conducted to investigate what extent and how vertical reinforcement elements may result in reinforcement effects from perspectives of bearing resistance contribution, energy dissipation, as well as volumetric response. Numerical results show that both the magnitude and the directional variation of normal contact forces govern the development of macroscopic strength and the reinforcing effects of joint protrusion height can be attributed to the accelerated energy dissipation across the particle assembly and the intensive mobilization of the geogrid.

Key words: geogrid; pullout behaviour; discrete element method (DEM); joint protrusion; fabric anisotropy; energy dissipation

1 Introduction

Geogrid has received increasing popularity in geotechnical engineering practice such as reinforced soil retaining walls, geosynthetic-reinforced and pile- supported embankments, and reinforced sand cushions [1-3]. It is commonly accepted that the overall performance of geogrid-reinforced soil systems depends heavily on the interaction between the backfill soil and the reinforcing elements [4, 5]. Plenty of experimental and theoretical studies [6-10] as well as finite element (FE) simulations [11, 12] have been carried out to evaluate the macro performance of geogrid-reinforced soil systems. Nevertheless, outcomes regarding the micro mechanism of soil-geogrid interaction still remain limited, owing partially to the inherent limitations of experimental, theoretical and finite element methods in performing micro-scale investigation. The micro-scale mechanism of soil-geogrid interaction is fundamental for refining reasonable design guidelines for geogrid- reinforced soil systems. It is hence necessary to identify the soil-geogrid interaction mechanism from a micro- scale perspective.

In principle, the discrete element method (DEM), which is a particle-based method [13], tends to be more capable of providing insight into the soil-geogrid interaction mechanism from a micro-scale perspective [14]. DEM possesses particular advantages in capturing microscopic responses of granular material such as particle sliding and rolling that are very likely to show up in practical cases. Some researchers have attempted to utilise DEM to study the geogrid-reinforced soil performance and evaluate the geogrid-soil interface behaviour [15-18]. However, these studies focused mainly on interface features including soil mobilization and geogrid deformation, but not particularly on the quantitative correlation between the macro and micro indices. Moreover, the geogrids covered in these studies were conventional plane types, and thus the corresponding findings are possibly not applicable to some new types of geogrids such as the three- dimensional (3D) reinforcing elements with vertical inclusions, as conceptually proposed by ZHANG et al [19, 20]. It has been demonstrated experimentally that a 3D reinforcing element not only produces a higher apparent soil cohesion but also gives rise to a much higher angle of shearing resistance of geogrid-soil systems [19, 20]. In other words, the pullout behaviour of a 3D geogrid can be quite different from that of a conventional plane geogrid. Therefore, to popularize the application of 3D geogrid in practice, further investigation should be performed to identify its pullout behaviour.

This work aims to bridge the gaps mentioned above. The objective is to characterize the pullout behaviour of geogrids in granular soil, with particularly emphasis on the pullout behaviour of geogrids with joint protrusions. The specific work presented in this work is divided into three parts. The first part introduces the strategies and procedures to model the pullout process of geogrids with or without joint protrusions by the use of PFC^3D. The second part focuses on analyzing the pullout behaviour of a conventional tri-axial geogrid in granular material. An effort is also made in this part to reveal the inherent correlation between the pullout force (a macroscopic parameter) and the fabric evolution (a microscopic index). The final part compares the pullout behaviour of 3D geogrids with different joint protrusions against that of a conventional geogrid, to demonstrate the influence of vertical joint protrusions on the reinforcing efficacy. The findings obtained from this work are expected to be helpful in enhancing the application of 3D geogrids in practice.

2 DEM modelling of geogrid pullout tests

2.1 Problem description

DEM is used to simulate a geogrid pullout test on sand specimen in a testing box subjected to a confining pressure. The testing box is created using a parallelepiped bounded by six rigid walls. After a low confining pressure is reached, a piece of geogrid is placed at the mid-depth of the testing box following the arrangements presented by MIAO et al [21], as depicted in Fig. 1. To prevent restriction of aggregates between the first row of transverse ribs and the pullout outlet, a length of 20 mm transverse ribs in front of the geogrid are removed. Two vertical walls are introduced to replace the left side wall to form a slot for subsequent pulling. The width of the outlet is 2.75 mm, which is slightly larger than the thickness of geogrid ribs (1 mm).

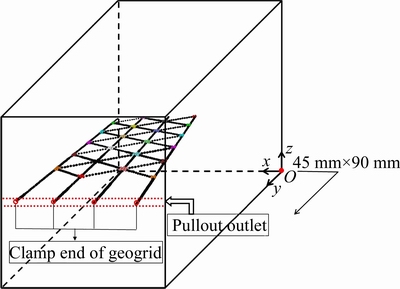
Fig. 1 Schematic diagram of test settings

2.2 Modelling of sand assembly

The sand used in this work is assumed to be the same as that used by ZHOU et al [22] and ZHENG et al [23]. The diameter of sand particles follows a uniform distribution ranging from 1.5 mm to 2 mm, and the initial porosity is 0.36. By matching the numerical modelling results and the data of laboratory tri-axial compression tests, ZHOU et al [22] have successfully calibrated a combination of microscopic parameters for the sand assembly. This combination of microscopic parameters is listed in Table 1, and will be used in the computation later.

Table 1 Input parameters for DEM modelling of sand assembly

As emphasized by LU et al [24] and YAN [25], sphere particles are not adequate for depicting the realistic mechanical features of sand; hence in this work the original sphere balls are transformed to quasi- elliptical ones, obeying mass and volume equivalent principle. Figure 2 illustrates the transforming algorithm; a quasi-elliptical particle is actually formed by three overlapping spheres. The dimensional relations between an original sphere ball and the corresponding quasi-elliptical particle are given by

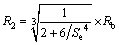                         (1)

                                   (2)

where R₁ and R₂ are the radii of the overlapped sphere balls shown in Fig. 2(b); R_b is the radius of the original sphere ball; S_e is the major-minor axis ratio of the quasi-elliptical particle, and S_e=2R₂/R₁. To approximately reflect the randomness of particle shape of the sand assembly, S_e is assumed to obey a uniform distribution within the interval of [1, 2]. Also, the quasi-elliptical particles are orientated randomly via a fish variable- urand, which is a random number obeying uniform distribution in the range [0.0, 1.0].

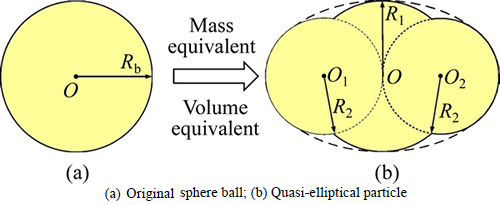
Fig. 2 Transforming process of a clump particle:

2.3 Modelling of geogrid

2.3.1 Plane tri-axial geogrid

A type of plane tri-axial geogrid with triangular apertures, as shown in Fig. 3, is considered in this work as a reference case. The mechanical behaviour and other information about this type of geogrid have been reported previously by MIAO et al [21]. In this work, the ribs and joints are connected by parallel bonds, the input microscopic parameters used in modelling are listed in Table 2.

Fig. 3 Modelling of geogrid with triangle apertures

2.3.2 3D geogrids with joint protrusions

ZHANG et al [19, 20] proposed a few new three-dimensional (3D) reinforcing geogrids featured by the presence of vertical inclusions such as joint protrusions. The laboratory experiments performed by YANG et al [2] also demonstrated that, in comparison with the conventional plane geogrids, a 3D geogrid is able to improve the working performance of the reinforced soil system by mobilizing evidently higher passive resistance against external load. Motivated by this observation, this work aims to make effort to explicitly figure out the influence of joint protrusions on the reinforcing efficacy. Therefore, besides the plane tri-axial geogrid, a group of 3D reinforcing geogrids with different sizes of joint protrusions are also considered in the following sections.

Table 2 Input parameters for DEM modelling of geogrid

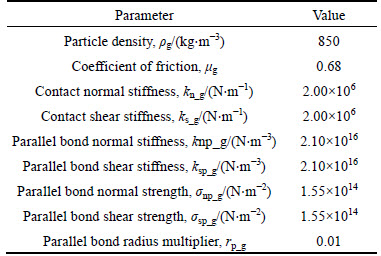
Figure 4 shows the DEM modelling strategies for the joint protrusions. Basically, joint protrusion is simulated by a clump of 3 overlapped balls, including a prime particle (the intermediate one, of which the diameter is expressed as d) and two identical subordinate particles. The two subordinate particles are constantly tangent to each other. In other words, the total height of a joint protrusion, h, is equal to 2 times the diameter of the two identical subordinate particles, d'. Particles consisting of the same joint protrusion are clumped to a rigid body. For each joint protrusion, only the prime particle is bonded to the rib particles, therefore, the geogid ribs do not directly interact with the subordinate particles of joint protrusions. Other input microscopic parameters involved in the modelling of 3D geogrids with joint protrusions are the same as those listed in Table 2.

Fig. 4 DEM modelling strategies for different sizes of joint protrusions:

2.4 Modelling procedures

The specific modelling procedures can be summarized as follows:

1) Enclose a simulation box (90 mm (L)×45 mm (W)×45 mm (H)) by six walls, and generate 41565 sphere balls in strict accordance with the prescribed porosity and particle size grading.

2) Transform the original sphere balls to quasi- elliptical clumps following the strategies introduced in Section 2.2, and cycle the assembly until the unbalanced contact force reaches an allowable level.

3) Apply a confining pressure of 10 kPa through adjusting the velocity of top and bottom walls.

4) Delete the aggregates that occupy the predefined region of geogrid particles, and install the geogrid particles.

5) Continue cycling and control the servo mechanism to obtain the prescribed normal stress.

6) Clear the displacement information of all the particles.

7) Initiate the pullout process by applying a constant velocity of 2×10^{-8 m/step on the end particles of longitudinal ribs. The magnitude of applied velocity is expected to accelerate the computational efficiency with an appropriate estimation of pullout resistance.}

8) Record the values of the key indices such as the pullout force, the energy term, and the tensile force, etc. at an interval of 0.15 mm, until the total displacement of the clamp end reaches 15 mm.

Figure 5 gives an overview of the initial stage of the pullout test specimen, note that for illustration purpose, the upper quarter of particles have been removed for easy visualisation of the geogrid. It can be found that, as expected, some aggregates are penetrated into the triangle apertures owing to the overburden surcharge. In addition, it is noted that the timestep is constantly assigned to be 1×10^-7 s/step in this work. This timestep is lower than the minimum value of all critical timesteps computed in different working conditions. Therefore the adjustment of timestep would ensure stable solutions for force-motion equations and facilitate further analysis.

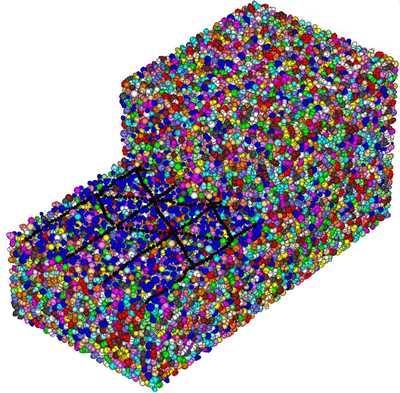
Fig. 5 PFC^3D model of a geogrid pullout test

3 Pullout behaviour of geogrids without joint protrusions

3.1 Pullout force

DEM simulations of pullout tests are conducted under five different normal stresses, i.e., 20 kPa, 50 kPa, 100 kPa, 200 kPa and 400 kPa. For a given normal stress and a given clamp end displacement, the pullout force can be determined by accumulating the unbalanced forces of the clamp end particles along the pull-out direction. Figure 6 shows the variation trends of pullout forces versus the clamp end displacement. As expected, the pullout force at each level of applied normal stress increases rapidly at first with the increase in clamp displacement, and finally tends to approach to a constant value. The clamp end displacement, beyond which the pullout force remains approximately constant or declined evidently, is referred to as the critical clamp end displacement in this work. Clearly, a higher normal stress not only gives rise to a much higher peak pullout force, but also produces an evidently higher critical clamp end displacement. Moreover, no obvious reduction in pullout force was observed within the prescribed maximum clamp end displacement (15 mm), implying that a relatively stable state could be reached providing that the embedded length of geogrid is sufficient and no transverse ribs are pulled out of the testing box.

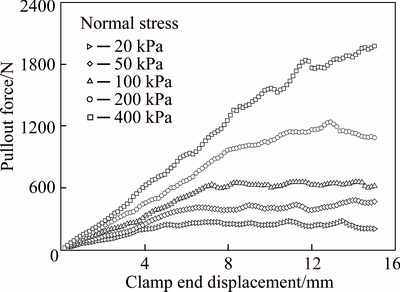
Fig. 6 Variation of pullout force versus clamp end displacement

3.2 Distributions of deformation and tensile force along geogrid

The case under a moderate normal stress of 100 kPa is adopted to represent the particle motion features during the pullout process of geogrid. Three typical clamp end displacements, namely 1.5 mm, 7.5 mm and 15.0 mm, are focused to analyze the deformation and tensile force distributions of geogrid. The top row of Fig. 7 shows the overall views of geogrid deformation at the three typical clamp end displacements. It can be seen that at a low level of clamp end displacement (e.g.1.5 mm), the geogrid apertures are able to maintain the original shapes. Nevertheless, with the increase in pullout force, transverse ribs deflect significantly because aggregates interlocked in the triangle apertures will restrict the geogrid from being pulled out.This phenomenon agrees well with the results reported by STAHL et al [26]. Furthermore, it is clear that the geogrid tends to shrink in the transverse direction, thus the actual aperture area during the pullout process decreases gradually in comparison with the original area.

In order to acquire the distribution regularity of tensile force along the geogrid, a subroutine is compiled in FISH language to output the coordinates of parallel bonds and the corresponding normal forces. Then, a continuous distribution of tensile force can be obtained using interpolation method; force distribution within the extruded section is not concerned because no interaction occurs there. Generally, tensile forces at different test stages distribute non-uniformly along the longitudinal direction. To be specific, a horizontal section, of which the length depends on the distance between the first row of transverse ribs and the frontal outlet, can be observed before a sudden reduction appears, implying that the modified segment without transverse ribs contributes little to the mobilization of pullout force and the applied external load is carried mainly by the first row of transverse ribs. This observation is consistent with the results presented by STAHL et al [26]. Due to the transverse shrinkage of geogrid and the decrease of effective aperture area, the magnitude of tensile force at a clamp end displacement of 15.0 mm (as shown in Fig. 7(c)) declined slightly in comparison with that at a clamp end displacement of 7.5 mm (as shown in Fig. 7(b)). The similar trend can also be found in the pullout force-displacement curve under a normal stress of 100 kPa (as shown in Fig. 6). On the whole, the overall trend of tensile force distribution, i.e. reducing gradually along the longitudinal direction and approaching to null at the terminal end, is in reasonable agreement with the analytical model proposed by SIEIRA et al [27]. As a matter of fact, the graphical analysis of geogrid behaviour, especially for the internal tensile force of geogrid which is difficult to be captured experimentally, provides an unique perspective to understand how the geogrid reacts during the pullout process.

3.3 Particle motion mobilized by geogrid pullout

Similarly, the case under a normal stress of 100 kPa is selected as an example. Particle motion features at the three typical clamp end displacements can be graphically visualized by plotting the displacement vectors of sand particles in scale, as shown in the left column of Fig. 8. Since the length of a displacement vector arrow is proportional to the magnitude, the gray level resulting from overlap of displacement vectors actually reflects the intensity of aggregate motion.

At the initial stage (u_clamp=1.5 mm), the frictional resistance, which is induced by relative particle motion, just needs to balance a small pullout force, so only particles in the very vicinity of geogrid are involved. As clamp end displacement and pullout force increase, the grey level in the whole region gradually deepens, and an evident grey level distinction can be observed between the near region adjacent to the geogrid and the far region. The near region forms a shearing band. When the clamp displacement comes to 15 mm, the thickness of shearing band (i.e. near region) reaches a maximum level.

Fig. 7 Deformation (a-c) and tensile force (a′-c′) distributions along geogrid under different clamp end displacements:

Fig. 8 Distribution of particle displacement vectors under different clamp end displacements ((a–c): Overall view; (a′–c′) Partial view):

Additionally, to better understand local particle motion characteristics around the stress boundary, the displacement vectors of sand particles beneath the upper wall are partially magnified, as shown in the right column of Fig. 8. It can be seen that, generally, the primary motion directions under the three typical clamp end displacements orientate downward, disorderly and upward, respectively. Since the normal stress is kept constant by the servo mechanism, this motion feature indicates that shearing dilation occurs in the assembly.

3.4 Distribution of contact forces and macro-micro correlation

3.4.1 Distribution of contact forces

Forces are transferred across the assembly via compression and sliding at contact points between ball-ball entities. The contact force at each contact point can be decomposed into normal and shear components relative to the contact plane. It is reported that the distribution and anisotropic evolution of the contact forces in normal direction mainly dominates the development of macroscopic shearing strength [28]. Therefore, the normal contact forces, f_n, are focused in the following analysis. The left column of Fig. 9 shows the distributions of normal contact forces at the three typical clamp end displacements. Note that the thickness of a short line shown in this figure stands for the magnitude of normal contact force at that point. On average, the distribution of f_n follows a similar trend with the tensile force distribution discussed earlier. With the progress of pullout process, the normal contact force gradually concentrates in the region of the first row of transverse ribs. Moreover, the orientation of f_n in the statistical analysis region tends to rotate anticlockwise since the outlet is set at the left side. This is consistent with the findings presented by DYER [29] and TRAN et al [14].

Through grouping the orientation of f_n that falls within predetermined angle intervals, BATHURST and ROTHENBURG [30, 31] [29, 30]proposed an approximate method to quantitatively assess the anisotropic features of normal contact force. The mathematical expression is:

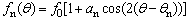               (3)

where f₀ is the mean value of normal contact forces in the region of interest; α_n is the magnitude of directional variation of f_n in each predefined angle interval; and θ_n is the rotational angle corresponding to the major principal direction of anisotropy, respectively. It should be noted that above fitting function is not suitable for a 3D analysis. Hence, normal force vectors in a 3D analysis should be projected to the yz plane first. The angle between the projected vector and the positive direction of z axis determines a certain interval in which the projected vector falls.

The above method is adopted in this work to statistically analyze the anisotropic features of normal contact forces during the geogrid pullout process. An interval of 10° is used following LAI et al [32]. The statistical analysis region of interest is defined by x[3.5, 41.5], y[y₁, y₂], z[25.0, 35.0] (unit: mm), where y₁ and y₂ denote the y-coordinates of the first and last row of transverse ribs, respectively. Note that y₁ and y₂ vary synchronously with the increase in clamp end displacement. The region of interest for statistical analysis is so chosen by referring to the displacement intensity in the upper part of the sand assembly, as depicted in the left column of Fig. 8. The right column of Fig. 9 presents the polar distribution of normal contact forces within the statistical analysis region during the pullout process. In this figure, the area of an irregular zone enclosed by broken lines reflects the average magnitude of f_n. It is explicit that the magnitude of f_n depends heavily on the pullout stage and differs significantly in different angle intervals. Furthermore, the major principal direction of anisotropy sharply rotates from approximately 0° at u_clamp=0 mm to 35.92° at u_clamp=1.5 mm, suggesting that force chain in the initial pullout stage is too weak to resist the horizontal pullout load. Whereas as the pullout process goes on, strong force network gradually develops, and the quantitative contact force indices, in terms of the degree of anisotropy α_n and the inclination of major principal direction θ_n, become less sensitive to the clamp end displacement, as shown in Figs. 9(b) and (c). In addition, the polar distribution of f_n changes from “peanut” shape in Fig. 9(b) to elliptical shape in Fig. 9(c), indicating that the directional variation of f_n declines along with the growth of f_n in the direction perpendicular to the major principal direction.

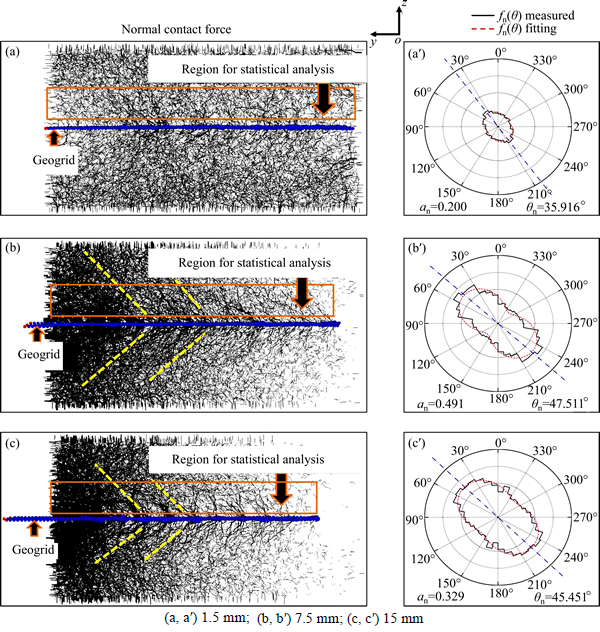
Fig. 9 Evolution of normal contact force (a-c) and fabric anisotropy (a′-c′) under different clamp end displacements:

It should be emphasized that in the above statistical analysis, the length of the projected vector in each angle interval constantly exceeds 0.75 times the original (3D) length. This means that the projection scheme is competent to reflect the actual 3D response of the assembly. In other words, this simplified statistical method can provide a reasonable insight into the nature of load transfer mechanism. Hence it will be used in the following sections to further clarify the correlation between macro and micro indices.

3.4.2 Correlation between macro and micro indices

SHI et al [28] proposed a correlation between the evolution of normal contact force and the shearing strength. This correlation merely depends on the degree of anisotropy α_n, regardless of the average magnitude of normal contact force. However, it should be noted that statistical indices with different magnitudes possibly share the same degree of anisotropy, as schematically shown in Fig. 10.

In fact, Eq. (3) indicates that the product of f₀ and α_n, rather than the α_n itself, is proportional to the fitted value. This suggests that a new variable R_n, defined by multiplying f₀ and α_n and termed fabric anisotropy coefficient, is possibly better in depicting the macroscopic behaviour (such as pullout force) originated from internal particle interaction. To prove this point, a comparison is drawn amongst the variation curves of pullout force (a macro index) and the two micro indices (α_n and R_n) with the increase in clamp end displacement. For easy reference, the variation curves of pullout force, α_n and R_n are normalized, respectively by the peak pullout force, maximum α_n and maximum R_n. The normalized results are shown in Fig. 11. It is observed that the variation trends of the three normalized curves are in good agreement before the pullout force reaches the peak value, while beyond the peak value point, neither α_n nor R_n matches the pullout force well. One possible reason is that a greater clamp end displacement will mobilize a larger scope of sand particles and it turns out that the main interaction zone exceeds the predefined statistical analysis region. Nevertheless, the correlation coefficient between normalized pullout force and normalized α_n is 0.864, while a much higher correlation coefficient of 0.948 can be reached if the magnitude of f_n is taken into consideration. Therefore, it is concluded that R_n is more appropriate to bridge the connection between microscopic fabric evolution and the pullout force at the clamp. This means that not only α_n but also the magnitude of f_n governs the development of macroscopic strength.

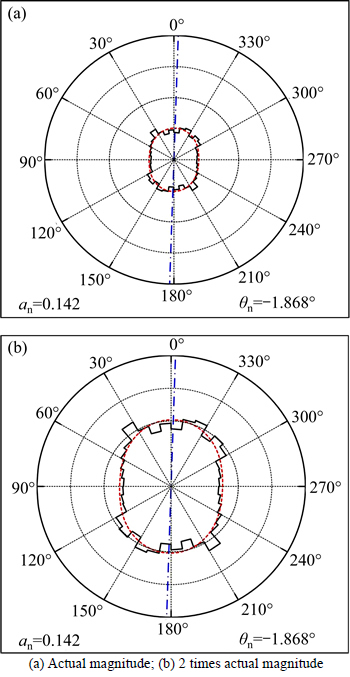
Fig. 10 Polar distribution of normal contact force at initial stage:

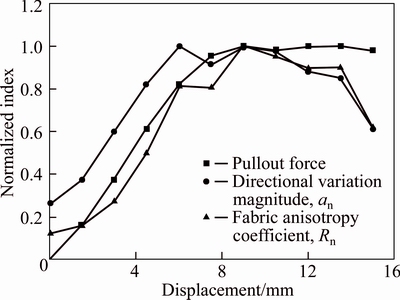
Fig. 11 Comparison amongst normalized variation curves of pullout force, α_n and R_n

4 Pullout behaviour of geogrids with joint protrusions

The results of the DEM simulations for the pullout tests of the five different 3D geogrids (referring back to Fig. 4) are discussed in the following sections to understand the influence of the size of joint protrusions on the pullout behaviour. The discussions are conducted in terms of pullout force, pullout resistance components, energy storage and dissipation as well as volumetric dilation.

4.1 Pullout force for 3D geogrids

Figure 12 plots the variations of the pullout forces for different 3D geogrids, the variation trend for each curve shown in this figure is approximately the same as that for the conventional plane tri-axial geogrid (referring to Fig. 6), namely increasing rapidly at first and finally approaching to a constant value. On the other hand, it is quite obvious that, for any given normal stresses and clamp end displacements, a 3D geogrid with larger joint protrusions constantly gives rise to an evidently higher pullout force, suggesting that the joint protrusions are able to enhance the pullout performance of geogrid in a substantial manner. The enhancement seems to be more significant under a relatively lower normal stress such as 100 kPa.

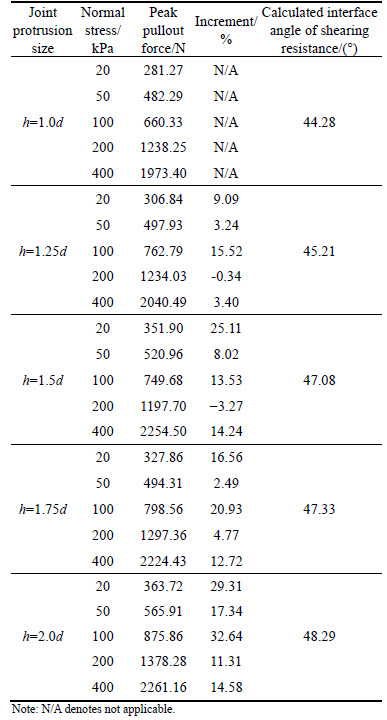
Further, the peak pullout forces during the entire pullout process for all the modelling cases are summarized in Table 3. The influence degree of joint protrusions can be quantified by the increasing peak pullout force, η, which can be determined as follows:

η=(F_pmax-F_pmax,0)/F_pmax,0                              (4)

where F_pmax,0 denotes the peak pullout force of the geogrid without joint protrusions (i.e. h=1.0d) under a given normal stress; and F_pmax denotes the peak pullout force of a 3D geogrid with joint protrusions under the same normal stress. The determined values of η for all modelling cases are given in Table 3. Take the case h=2.0d as an example, the value of η can even reach up to 32.64% when the normal stress is 100 kPa, demonstrating again that the introduction of joint protrusions is a promising way to improve the work performance of geogrid.

SUGIMOTO et al [12] presented a method to estimate the average shear stress τ_avg:

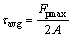                                (5)

where F_pmax is the peak value of pullout force and A is the gross area of geogrid embedded in soil. By using this equation, the average shear stress τ_avg for each 3D geogrid under each normal stress can be easily determined. If a straight line is used to fit the relation between the average shear stress τ_avg and the normal stress, the slope of the fitting line actually represents the angle of shearing resistance δ—a very important design parameter. The last column of Table 3 provides the values of δ for the geogrids with different sizes of joint protrusions. It can be seen that the obtained δ for all modelling cases is higher than the angle of shearing resistance of the sand used.This is owing to the resistance contributed by transverse ribs and the arching effect resulting from the stiffness difference between soil and geogrid, as confirmed by SUKSIRIPATTANAPONG et al [33]. More importantly, the angle of shearing resistance δ increases with the increase in the size of joint protrusions, signifying that a higher level of interaction can be potentially gained by an enhancement in joint height.

Fig. 12 Variation of pullout force for different 3D geogrids:

Table 3 Reinforcing efficacy in different modelling cases

4.2 Pullout resistance components

The preceding subsection has demonstrated the substantive influence of nodal protrusions on the work performance of geogrid. In this subsection, the cases under a normal stress of 100 kPa are adopted to reveal the microscopic mechanism that nodal protrusions affect the work performance.

It is generally acknowledged that the pullout force consists of two components: the frictional resistance on geogrid surface and the passive bearing resistance caused by transverse members. However, it is rather difficult to quantify the magnitudes of the two components neither experimentally nor analytically. Whereas in DEM, the frictional force relies on the prescribed friction coefficient between the two contacting entities [34], hence the frictional resistance can be eliminated if the friction coefficient of geogrid particles is set to 0. In this fictitious case, the pullout force is equal to the passive bearing resistance, and then the true magnitude of frictional resistance can be obtained by excluding the component of passive bearing resistance from the total pullout force in the actual case. Figure 13 shows the mobilization of the two pullout resistance components for the 3D geogrids with different sizes of joint protrusions. The results show that a substantive difference can be observed amongst resistance mobilization curves for different sizes of joint protrusions, particularly when the clamp end displacement exceeds 6 mm. When the joint height h increases from 1.0d to 2.0d, the passive bearing resistance mobilized at u_clamp=12 mm rises by 77.89% from 306.18 N to 544.62 N, while the friction resistance mobilized at the same clamp end displacement reduces by 6.78% from 323.18 N to 301.25 N, since evidently higher dilation appears with the increase of the joint height, as illustrated in Fig. 17. It turns out that the total pullout force increases by 34.40% from 629.36 N to 845.87 N. Comparatively, the passive bearing resistance plays a dominant role and accounts for 64.39% of the total increment of pullout force.

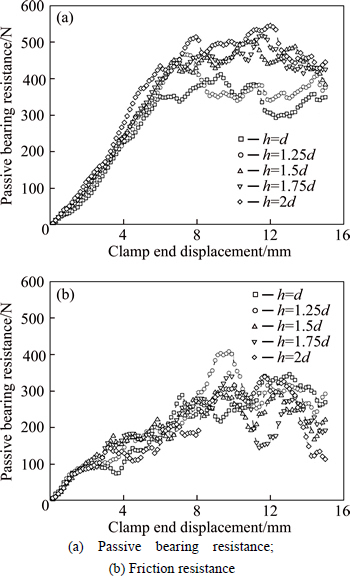
Fig. 13 Mobilization of pullout resistance components for different 3D geogrids:

4.3 Energy storage and dissipation

The evolution of energy storage and dissipation, which is important in understanding the inherent mechanical behaviour of granular materials [35, 36], is systematically examined in this subsection. PFC3D provides a total of 6 intrinsic energy terms including boundary work done by walls E_w, total accumulated body work E_b, total strain energy stored in the parallel bonds E_pb, energy dissipated by frictional sliding E_f, kinetic energy E_k, and strain energy stored at aggregate contacts E_s. Among them, the energy terms stored and dissipated in the particle system are of particular concern in this work. Specifically, these energy terms can be categorized into two groups, namely energy consumed (stored or dissipated) by particle assembly E_c (E_c=E_f+ E_s+E_k) and energy stored in the parallel bonds of geogrid E_pb.

All the energy terms of interest are traced and recorded for different modelling cases. It is found that the magnitudes of E_s and E_k are marginal in comparison with the magnitude of E_f, therefore E_s and E_k are omitted in analysis of E_c. Figure 14 presents the evolution of E_c during the pullout process. It can be observed that in each case E_c rises in a parabolic form. The rapid growth in the later stage can be ascribed to the sufficient mobilization of aggregates. Moreover, a geogrid with bigger joint protrusions exhibits a higher capacity of energy consumption. This is not surprising since particles in a larger region can be gradually mobilized.

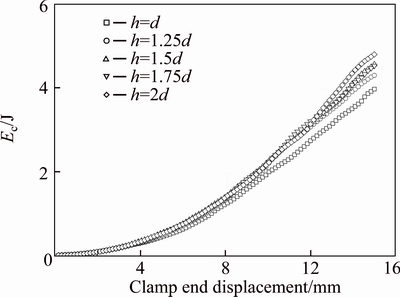
Fig. 14 Evolutions of E_c in different modelling cases

A comparison is further drawn between the magnitudes of E_c consumed in the modelling cases with and without considering the friction coefficient of geogrid particles. The comparison results is shown in Fig. 15. Note that in this figure the magnitude of E_c without considering the friction coefficient of geogrid particles is actually consumed merely by the passive bearing members. It is found that the energy consumed merely by passive bearing members accounts for nearly 60% of the total E_c, and the increment of E_c arising from the joint protrusions can be up to 20%.

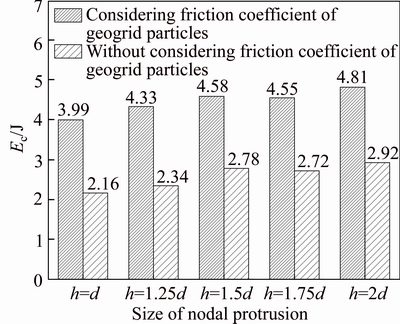
Fig. 15 Comparison between magnitudes of E_c with and without considering friction coefficient of geogrid particles (u_clamp=15 mm)

Another energy term E_pb is analyzed in Fig. 16 to demonstrate the mobilization of geogrid. As expected, the magnitude of energy stored in parallel bonds has a positive correlation with the height of joint protrusions. Also, it is noticed that E_pb follows approximately the same pace with the pullout force. In summary, the quantitative evaluation of energy terms enables deep insight into the contribution of the vertical reinforcing elements, and the effect of joint protrusions mainly includes 3 aspects: 1) accelerating the energy dissipation across the particle assembly; 2) promoting the contribution of passive bearing members; and 3) enhancing the mobilization of geogrid.

Fig. 16 Strain energy stored in parallel bonds of geogrid

4.4 Volumetric dilation

INDRARATNA et al [37, 38] successfully captured the volumetric change by recording the displacement of the top wall in a DEM simulation. Similarly, in this work the relative displacement between the top and bottom walls, of which the velocities are dynamically adjusted to guarantee a given normal stress, is recorded by a user-defined subroutine to evaluate the global volumetric change of the particle system. Figure 17 depicts the associated change of volume in different modelling cases. It is explicit that under an identical normal stress of 100 kPa, the volumetric dilation is significantly affected by the size of joint protrusions. Besides, the presence of joint protrusions reduces the critical clamp end displacement, at which the system transits from volumetric compression to volumetric dilation. This means that the presence of joint protrusions will promote the rearrangement and self-organization of aggregates to resist the external load.

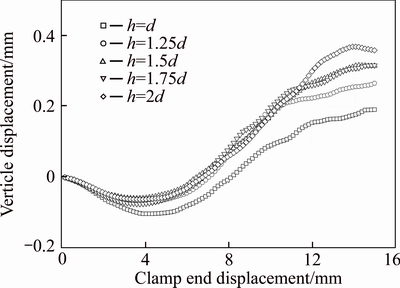
Fig. 17 Volumetric response of aggregates in different modelling cases

5 Conclusions

Based on the calibrated model of soil and geogrid, a series of DEM simulations of pullout test have been conducted to visualize the geogrid-soil interactions and promote the understanding of geogrid reinforcement mechanism under special consideration of joint protrusions. The main conclusions regarding the interface behaviour and the enhancing effect of joint protrusions can be summarized below:

1) The association between geogrid and soil is qualitatively detected by a combined observation of typical interface characteristics including deformation and force distribution in geogrid, displacement and contact force developed among particles, respectively. The mobilizations of soil and geogrid under three representative displacements could reflect that how geogrid-soil interaction develops under pullout loads.

2) More accurate connection between macroscopic strength development and microscopic fabric evolution is bridged as the introduction of fabric anisotropy coefficient R_n. Correlation analysis testifies that both the magnitude and the directional variation of normal contact force govern the development of macroscopic strength.

3) The partial enhancement in joint height significantly increases the interaction intensity and therefore is a promising way to improve the work performance of geogrid. Specific analysis at double scales reveals that the existence of joint protrusions promotes the contribution of bearing members and the rearrangement and self-organization of aggregates to resist the external load, as a result, the energy dissipation across the particle assembly is accelerated.

References

[1] ZHANG J, ZHENG J J, CHEN B G, YIN J H. Coupled mechanical and hydraulic modeling of a geosynthetic-reinforced and pile- supported embankment [J]. Computers and Geotechnics, 2013, 52: 28-37.

[2] YANG G, LIU H, LV P, ZHANG B. Geogrid-reinforced lime-treated cohesive soil retaining wall: Case study and implications [J]. Geotextiles and Geomembranes, 2012, 35: 112-118.

[3] HEERTEN G. Reduction of climate-damaging gases in geotechnical engineering practice using geosynthetics [J]. Geotextiles and Geomembranes, 2012, 30: 43-49.

[4] BHANDARI A, HAN J. Investigation of geotextile–soil interaction under a cyclic vertical load using the discrete element method [J]. Geotextiles and Geomembranes, 2010, 28(1): 33-43.

[5] WANG Z, RICHWIEN W. A study of soil-reinforcement interface friction [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(1): 92-94.

[6] PALMEIRA E M. Soil–geosynthetic interaction: Modelling and analysis [J]. Geotextiles and Geomembranes, 2009, 27(5): 368-390.

[7] TEIXEIRA S H, BUENO B S, ZORNBERG J G. Pullout resistance of individual longitudinal and transverse geogrid ribs [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(1): 37-50.

[8] SHINODA M, BATHURST R J. Lateral and axial deformation of PP, HDPE and PET geogrids under tensile load [J]. Geotextiles and Geomembranes, 2004, 22(4): 205-222.

[9] PALMEIRA E M. Bearing force mobilisation in pull-out tests on geogrids [J]. Geotextiles and Geomembranes, 2004, 22(6): 481-509.

[10] MCDOWELL G, HARIRECHE O, KONIETZKY H, BROWN S, THOM N. Discrete element modelling of geogrid-reinforced aggregates [J]. Proceedings of the ICE-Geotechnical Engineering, 2006, 159(1): 35-48.

[11] KHEDKAR M, MANDAL J. Pullout behaviour of cellular reinforcements [J]. Geotextiles and Geomembranes, 2009, 27(4): 262-271.

[12] SUGIMOTO M, ALAGIYAWANNA A. Pullout behavior of geogrid by test and numerical analysis [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(4): 361-371.

[13] CUNDALL P A, STRACK O D. A discrete numerical model for granular assemblies [J]. Geotechnique, 1979, 29(1): 47-65.

[14] TRAN V D H, MEGUID M A, CHOUINARD L E. A finite–discrete element framework for the 3D modeling of geogrid–soil interaction under pullout loading conditions [J]. Geotextiles and Geomembranes, 2013, 37: 1-9.

[15] WANG Z, JACOBS F, ZIEGLER M. Visualization of load transfer behaviour between geogrid and sand using PFC2D [J]. Geotextiles and Geomembranes, 2014, 42(2): 83-90.

[16] TONG L, WANG Y H. DEM simulations of shear modulus and damping ratio of sand with emphasis on the effects of particle number, particle shape, and aging [J]. Acta Geotechnica, 2014, 10(1): 117-130.

[17] NGO N T, INDRARATNA B, RUJIKIATKAMJORN C. DEM simulation of the behaviour of geogrid stabilised ballast fouled with coal [J]. Computers and Geotechnics, 2014, 55: 224-231.

[18] CHEN C, MCDOWELL G R, THOM N H. Discrete element modelling of cyclic loads of geogrid-reinforced ballast under confined and unconfined conditions [J]. Geotextiles and Geomembranes, 2012, 35: 76-86.

[19] ZHANG M X, ZHOU H, JAVADI A A, WANG Z W. Experimental and theoretical investigation of strength of soil reinforced with multi-layer horizontal–vertical orthogonal elements [J]. Geotextiles and Geomembranes. 2008, 26(1): 1-13.

[20] ZHANG M X, JAVADI A, MIN X. Triaxial tests of sand reinforced with 3D inclusions [J]. Geotextiles and Geomembranes, 2006, 24(4): 201-209.

[21] MIAO Chen-xi, ZHENG Jun-jie, CUI Ming-juan, XIE Ming-xing, ZHAO Jian-bin. Study of influence of joint protuberance on geogrid reinforcement performance by discrete element method [J]. Rock and Soil Mechanics, 2014, 35(4): 1181-1186. (in Chinese)

[22] ZHOU Jian, JIAN Qi-wei, ZHANG Jiao, GUO Jian-jun. Coupled 3D discrete-continuum numerical modeling of pile penetration in sand [J]. Journal of Zhejiang University: Science A, 2012, 13(1): 44-55.

[23] ZHENG Jun-jie, MIAO Chen-xi, XIE Ming-xing, ZHANG Jun. Interface properties and influence of particle size on geogrid reinforcement performance by DEM [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1423-1428. (in Chinese)

[24] LU M, MCDOWELL G R. The importance of modelling ballast particle shape in the discrete element method [J]. Granular Matter, 2006, 9(1, 2): 69-80.

[25] YAN W M. Fabric evolution in a numerical direct shear test [J]. Computers and Geotechnics, 2009, 36(4): 597-603.

[26] STAHL M, KONIETZKY H, TE KAMP L, JAS H. Discrete element simulation of geogrid-stabilised soil [J]. Acta Geotechnica, 2013, 9(6): 1073-1084.

[27] SIEIRA A C C F, GERSCOVICH D M S, A S F J. Displacement and load transfer mechanisms of geogrids under pullout condition [J]. Geotextiles and Geomembranes, 2009, 27(4): 241-253.

[28] SHI Dan-da, ZHOU Jian, LIU Wen-bai, DENG Yi-bing. Exploring macro-and micro-scale responses of sand in direct shear tests by numerical simulations using non-circular particles [J]. Chinese Journal of Geotechnical Engineering, 2010, 32(10): 1557-1565. (in Chinese)

[29] DYER M. Observation of the stress distribution in crushed glass with applications to soil reinforcement [D]. Oxford: University of Oxford, 1985.

[30] BATHURST R J, ROTHENBURG L. Observations on stress-force-fabric relationships in idealized granular materials [J]. Mechanics of Materials, 1990, 9(1): 65-80.

[31] ROTHENBURG L, BATHURST R J. Analytical study of induced anisotropy in idealized granular materials [J]. Geotechnique, 1989, 39(4): 601-614.

[32] LAI H J, ZHENG J J, ZHANG J, ZHANG R J, CUI L. DEM analysis of “soil”-arching within geogrid-reinforced and unreinforced pile-supported embankments [J]. Computers and Geotechnics, 2014, 61(9): 13-23.

[33] SUKSIRIPATTANAPONG C, HORPIBULSUK S, CHINKULKIJNIWAT A, CHAI J C. Pullout resistance of bearing reinforcement embedded in coarse-grained soils [J]. Geotextiles and Geomembranes, 2013, 36: 44-54.

[34] Itasca. Particle flow code in three dimensions (PFC3D) [M]. Minnesota: Itasca Consulting Group Inc, 2008.

[35] WANG J F, YAN H B. DEM analysis of energy dissipation in crushable soils [J]. Soils and Foundations, 2012, 52(4): 644-657.

[36] ZHANG W C, WANG J F , JIANG M J. DEM-aided discovery of the relationship between energy dissipation and shear band formation considering the effects of particle rolling resistance [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(9): 1512-1527.

[37] INDRARATNA B, NGO N T, RUJIKIATKAMJORN C. Behavior of geogrid-reinforced ballast under various levels of fouling [J]. Geotextiles and Geomembranes, 2011, 29(3): 313-322.

[38] INDRARATNA B, NGO N T, RUJIKIATKAMJORN C, VINOD J S. Behavior of fresh and fouled railway ballast subjected to direct shear testing: Discrete element simulation [J]. International Journal of Geomechanics, 2014, 14(1): 34-44.

(Edited by FANG Jing-hua)

Cite this article as: MIAO Chen-xi, ZHENG Jun-jie, ZHANG Rong-jun, XIE Ming-xing, YIN Jian-hua. Visualization of pullout behaviour of geogrid in sand with emphasis on size effect of protrusive junctions [J]. Journal of Central South University, 2017, 24(9): 2121–2133. DOI:https://doi.org/10.1007/s11771-017-3621-7.

Foundation item: Projects(51278216, 51478201) supported by the National Natural Science Foundation of China

Received date: 2015-10-11; Accepted date: 2016-03-29

Corresponding author: ZHENG Jun-jie, Professor, PhD; Tel: +86–27–87557024; E-mail: zhengjj@hust.edu.cn