DOI: 10.11817/j.issn.1672-7207.2019.01.005
平面磨削条件下温度阈值对残余应力形成的影响
温俊1, 2,唐进元1, 2,郑金超1, 2
(1. 中南大学 高性能复杂制造国家重点实验室,湖南 长沙,410083;
2. 中南大学 机电工程学院,湖南 长沙,410083)
摘要:考虑平面磨削条件下的热力耦合作用,研究磨削温度阈值对残余应力形成的影响。基于热弹塑性理论,构建预测磨削热产生残余应力的计算模型;加载椭圆移动热源,使用COMSOL有限元软件进行热-弹塑性多物理场耦合计算,得到磨削区域温度场分布与不同磨削参数对工件表层产生初始塑性应变的影响,从而定量分析磨削温度与磨削残余应力间的相互关系;通过平面磨削实验测得磨削工件表面温度场及磨削后工件表层残余应力,并与数值计算结果进行对比分析。研究结果表明:磨削温度计算值与实测值相对误差在5%以内;磨削温度产生的初始塑性应变对最终残余应力场有较大影响;在一定磨削参数下,可以确定形成初始热塑性应变及残余拉应力的磨削温度阈值。
关键词:磨削温度;残余应力;热力耦合;磨削温度阈值
中图分类号:TH123.4 文献标志码:A 文章编号:1672-7207(2019)01-0530-10
Influence of plane grinding temperature threshold on formation of residual stress
WEN Jun1, 2, TANG Jinyuan1, 2, ZHENG Jinchao1, 2
(1. State Key Laboratory for High Performance Complex Manufacturing, Central South University, Changsha 410083, China;
2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
Abstract: With consideration of the thermo-mechanical coupling under the condition of plane grinding, the effect of grinding temperature threshold on the formation of residual stress was studied. Based on the thermo-elastoplasticity theory, a calculation model for predicting the residual stress generated by grinding heat was constructed. The elliptical moving heat source was loaded, and the thermo-mechanical multiphysics coupling calculation was performed using COMSOL finite element software. The temperature field distribution in the grinding region and the influence of the parameters on the initial plastic strain of the workpiece surface was obtained, and the relationship between the grinding temperature and the residual stress of grinding was quantitatively analyzed. The surface temperature field of the workpiece and the residual stress of the workpiece surface after grinding were measured by plane grinding experiment, and they were compared with the numerical calculation results. The results show that the error between the calculated and measured values of the grinding temperature is less than 5%, and the initial plastic strain generated by the grinding temperature has great influence on the final residual stress field. With certain grinding parameters, the grinding temperature threshold for initial thermoplasticity strain and residual tensile stress can be determined.
Key words: grinding temperature; residual stress; thermal-mechanical coupling; grinding temperature threshold
磨削加工常作为加工过程中的最后一道工序,往往对工件表面质量有决定性作用。在磨削过程中,磨削区域形成高强度热源,大量磨削热传入工件中。磨削热产生的残余应力一般为残余拉应力,这对工件使用性能有很大影响[1-2]。残余拉应力的大小、变化梯度和分布范围会影响零件表层疲劳强度、零件的抗腐蚀性能以及使零件表面产生微观裂纹等[3]。磨削后工件表层残余应力的形成主要受热应力、机械应力以及材料相变应力三者耦合作用影响[4-5]。在某些磨削条件下,可以不考虑材料相变应力对残余应力的作用,认为磨削中残余应力主要由磨削力及磨削温度产生,通常机械力对工件造成挤压变形,磨削后在表层形成残余压应力;而磨削热则形成拉应力[6]。为了研究这两者之间的相互联系,有必要对残余拉应力产生的磨削温度临界值进行定量计算,通过改变磨削参数,控制磨削力热,进一步控制磨削表层残余应力组成及残余应力层深度。在稳态磨削条件下,最大等效应力受磨削温度影响,根据不同工件材料参数,当磨削温度达到临界值时,材料开始产生塑性屈服和热塑性变形,而热塑性变形是磨削后产生残余拉应力的主要原因[7]。目前,国内对这方面的研究较少,定量计算产生残余应力的磨削温度阈值及严格推导计算弹塑性材料固体内由于热源移动产生的应力场理论模型更少。移动热源最早的理论模型是BLOK[8]提出来的,用于计算上、下相互滑移面间的接触温度;之后,JAEGER[9]提出了详细描述半无限大到无限大区域内的带状移动热源温度场的解析模型,并提出了计算移动热源接触表面最高温度的理论;LI等[10]根据磨削过程中磨粒分布高度,定义了磨粒与工件接触阶段,建立了不同磨削阶段磨粒点热源模型,并与磨削温度实验结果进行对比验证,从微观角度解释了磨削温度场的形成;POMBO等[11]研究了磨削接触弧长对磨削温度场的影响,并通过实验进行了验证,给出了较合理的磨削接触弧长计算公式。与温度场研究不同的是,弹塑性材料固体内热源移动产生应力场的理论模型还很缺乏,MISHRA等[12]通过耦合准静态温度场并应用有限元分布在弹塑性体内仿真,计算得出带状热源在半无限大空间内表面残余应力的分布情况,而MISHRA等[12]计算的模型并没有计算冷却到室温时工件的残余应力场,因此,这样得到的残余应力并不完善。HAMDI等[13]在磨削残余应力计算中加入了机械力及相变引起的应力场变化,SHAH等[14-16]也讨论了机械力及相变应力在残余应力中的作用。任敬心等[17]讨论了GH33A高温合金的磨削温度与残余应力间的联系,并通过实验分析了不同磨削条件下磨削温度对残余应力的影响及不同磨削参数下工件表层残余应力和应力层深度;HAMDI等[13]分析了温度引起残余应力变化的条件,但未考虑热力耦合作用对残余应力的影响,也没有通过实验进行分析验证。为此,本文作者通过研究椭圆分布移动热源,经计算得出磨削工件温度场;使用埋入式热电偶对磨削温度进行测量,得到磨削区域温度场,并与计算结果进行对比,分析得到椭圆分布热源能有效仿真磨削区域温度场。在温度场基础上,运用热弹塑性理论讨论热塑性变形的温度阈值;通过热力耦合作用,运用有限元计算磨削温度及磨削力对工件表层残余应力的影响,分析在一定磨削工况下,产生残余拉应力的磨削温度阈值;对实验工件表面残余应力进行测量,验证产生残余拉应力磨削温度阈值的准确性。
1 理论模型
1.1 模型参数
图1所示为平面磨削过程示意图,其中,vs为砂轮磨削工件表面转速,vw为工件相对砂轮的进给速度,аp为切削深度,lb为砂轮宽度,lw为工件长度,hw为工件高度,bw为工件宽度,qt为磨削产生的热源强度。若忽略磨削过程中材料去除量,则磨削表面可以近似看作是1个压力及热源分布在工件上移动,沿长度和宽度方向都是有限的区域,平均压力为真实接触区域法向磨削力,而平均热源强度为单位时间内磨削区域产生的热量。热流密度通常在磨削接触弧长内呈三角形分布或椭圆分布。本文使用椭圆热流密度分布,图2所示为砂轮工件接触区域示意图。工件材料采用12CrNi4A航空齿轮钢,砂轮选用CBN砂轮,其物理学参数如表1所示。
为了求解移动热源在半无限大的空间内产生的温度和应力,将砂轮看作在表面上以速度vw移动的带状热源,热源的长度为砂轮和工件的接触长度lc,工件砂轮间几何接触长度lc可以近似为
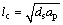 (1)
(1)
式中:ds为砂轮直径,mm;аp为砂轮切削深度,mm。
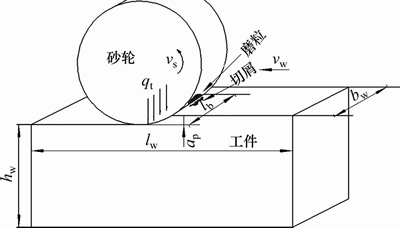
图1 磨削过程示意图
Fig. 1 Schematic diagram of grinding process
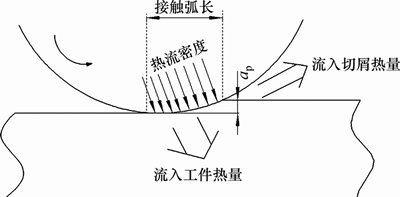
图2 砂轮与工件接触区域示意图
Fig. 2 Schematic diagram of wheel and workpiece contact area
Peclet数是用于反映热源移动速度与热传导参数间关系的量纲一参数,它决定了热量耗散的速度[18],用P表示Peclet数。
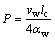 (2)
(2)
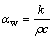 (3)
(3)
式中:αw为热扩散系数;k为导热系数,W/(m·K);ρ为密度,kg/m3;c为比热容,J/(kg·K)。
在热流密度分布理论方面,一些研究者认为由传统的热流密度分布不能得出精确的磨削温度场分布,因为在温度上升阶段,磨削区域在一个很短的时间内达到峰值温度,由传统矩形热源分布并不能有效得出磨削过程中温度上升的趋势。本文考虑磨削过程中砂轮与工件间的接触形式,结合赫兹接触压力分布中圆柱与平面接触呈椭圆形分布的情况,选择与实际磨削情况更贴近的椭圆热流密度分布,其表达式见式(4)。在有限元计算中,热源以速度vw在工件表面移动,接触弧长为lc;q(x)为椭圆热源在接触弧长上的热流密度,在x=0时,q(x)达到最大值;在x=a时,q(x)=0,a=1/2lc,如图3所示。
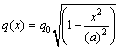 (4)
(4)
 (5)
(5)
式中:q0为椭圆热流密度的最大值;Q为流入工件的热源强度,W/mm2。
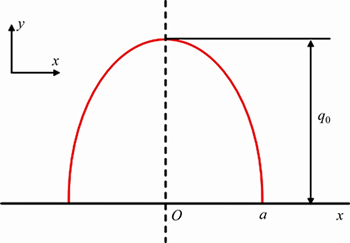
图3 椭圆热流密度分布模型
Fig. 3 Distribution model of elliptical heat flux
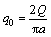 (6)
(6)
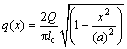 (7)
(7)
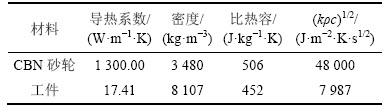
用于仿真计算的砂轮和工件材料物理学参数及磨削过程中的参数见表1。
表1 砂轮和工件热力学参数
Table 1 Thermodynamic parameter of wheel and work-piece
1.2 平面磨削温度场解析方程
根据CHOI[4]的研究成果可得出如下二维瞬态热传导方程:
 (8)
(8)
工件与环境换热边界条件为
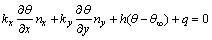 (9)
(9)
式中:kx为沿x方向上的热传导系数,W/(m·K);ky为沿y方向上的热传导系数,W/(m·K)。假设对流传导只沿着上表面传递,由此可以用有限元求得移动热源沿表面移动过程中的温度历程[19]。
1.3 基于应力应变场的残余应力计算
热弹塑性材料应力应变的计算模型由文献[20-21]得出。总应变增量(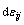 )为材料弹性增量(
)为材料弹性增量( )、塑性增量(
)、塑性增量( )和热变形增量(
)和热变形增量( )的总和,即
)的总和,即
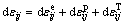 (10)
(10)
以上各量将在有限元中计算,残余应力的有限元计算过程分为2步:1) 假设磨削过程为准静态过程,计算温度场及应力应变场在磨削过程中的分布情况;2) 根据步骤1)计算得到的准静态结果,仿真最终冷却后工件表面的应力应变场,得到工件表层残余应力场分布。在这2步中,都应用了热力耦合机制,先是由热源移动计算温度分布,然后计算工件材料应力应变。方程(1)~(10)为平面磨削热力耦合残余应力计算理论模型,为提高计算效率,借助有限元软件COMSOL进行数值求解。
2 基于COMSOL的残余应力仿真计算与分析
2.1 有限元网格划分
网格的密度取决于加载在工件上的载荷及边界条件。在磨削过程中,由于磨削区域存在瞬时高温及温度梯度,越靠近表面,温度梯度越大。在计算应力应变场时,由于存在弹塑性变形温度,网格精度不够或者网格划分不合理都会导致网格产生畸变,导致非线性不收敛问题。在近表面处需要选用足够细密的网格,在温度梯度变化小的区域则选用粗略网格,以提高计算速度。
在本次计算中,假设工件为1个2D半无限大平面,高为0.03 m,宽为0.06 m;有限元网格由三角形网格和四边形网格组合而成,单元总数超过24 000个,其中最小单元网格尺寸为10-4 m,如图4所示。
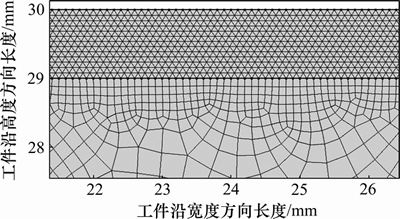
图4 工件表层网格划分
Fig. 4 Meshing of work-piece surface
2.2 初始和边界条件
工件及室温的初始时刻(t=0 s)温度设置为θ=25 ℃。在磨削接触区域和下表面以外的表面给定1个线性对流传导项:
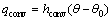 (11)
(11)
式中:hconv为对流传导系数,W/(m2·K);θ为半无限大工件温度,℃;θ0为周围环境温度,℃。
这里的冷却媒质为空气对流,下表面热流流出量认为趋近于0 W/mm2。
2.3 加载热源
热源项的加载通常认为是可以移动的分布热源,该热源沿着工件上表面移动,忽略材料去除对热源的影响。经典的热源模型有JAEGER[9]提出的矩形热源以及所衍生的三角形热源。WANG等[22-23]利用热电偶测试磨削区域温度,发现在磨削区域在短时间达到温度峰值,认为由三角形热源所计算的温度场更加符合磨削实际。SHAH等[14]结合赫兹压力和热流密度分布理论,假设接触区域摩擦因数均匀一致,利用滚压滑移接触方法即1个圆柱体和1个平面间的Hertz接触压力分布建模,接触区域为1个椭圆形,所以,认为热源形状为椭圆分布的假设是可行的。图5所示为热源在工件上移动的原理示意图。

图5 热源及工件表面对流
Fig. 5 Heat source and work-piece surface convection
2.4 基于热力耦合的残余应力分析
与计算温度场不同的是,在加入热弹塑性变形后,单元节点位移变形,材料的形变需要根据网格节点上高斯点的序列排序。为了保证整体完整性,计算中采用网格自适应,通过几何形变控制网格单元节点变化,保证计算过程中非线性收敛[12]。
砂轮在工件表面移动时,热源强度设定在砂轮和工件脱离接触时变为0 W/mm2,这样避免了重复计算。当边界条件设置的对流换热系数不同时,工件材料在磨削后表面温度下降速率也有所不同,本文的磨削条件为干磨削,未使用磨削液,工件表面温度冷却速率较慢,经计算,当冷却时间为5 min时,工件材料表面温度趋近于室温,工件内部温度差在2 ℃以内,不会对最终工件表面残余应力造成影响,残余应力更贴近实际磨削残余应力。增加冷却时间不会对计算结果造成影响,反而会增加计算时间,降低计算效率;若冷却时间设置太低,则会由于工件表面温度未与室温平衡,在工件内部存在温度梯度,造成残存热应力,导致最终工件表面残余应力计算结果存在误差。因此,设置工件冷却时间为5 min,材料内部应力接近磨削后残余的应力。
2.4.1 温度场分布
在磨削时长t=2 s时计算得到的温度(曲线沿着水平线方向延伸)以及温度在磨削深度(y/a=2y/lc)方向上的变化如图6所示。从图6可见:在热源强度及Peclet数为固定值时,在磨削深度方向上随着深度增加,温度峰值逐渐降低,越靠近表面,温度变化梯度越大,与BLOK[24]的分析方法得到的结果对比具有较好的一致性。在磨削过程中,表面温度在磨削时长t=2 s时的分布曲线及不同热源强度(Q)输入下温度场分布如图7所示。从图7可见:随着加载的热源强度逐渐降低,砂轮和工件接触区域的峰值温度也随之降低。
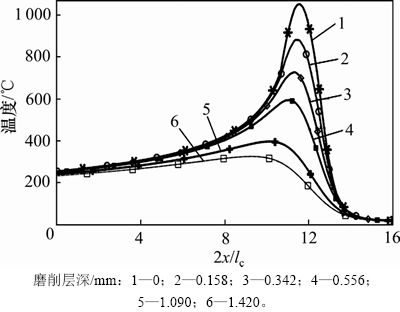
图6 工件不同深度温度分布
Fig. 6 Work-piece temperature distribution in different depths
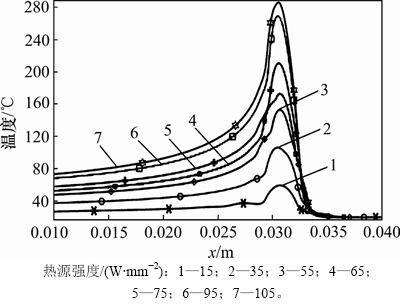
图7 不同热源下工件表面温度分布
Fig. 7 Surface temperature distribution under different heat sources
改变热源移动的量纲一参数P,工件表面的峰值温度与P的关系如图8所示。从图8可以看出:随着工件进给速度增大,磨削区域最高温度逐渐降低;工件进给速度越大,磨削温度越低。
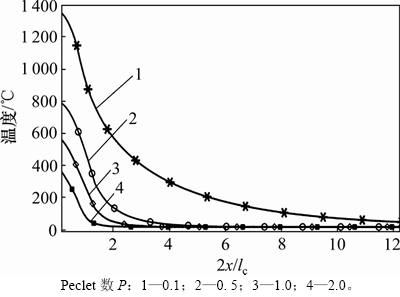
图8 不同工件移动速度表面温度分布
Fig. 8 Surface temperature distribution of work-piece under different feed speeds
2.4.2 工件弹塑性应力应变
移动热源在弹塑性固体中产生的瞬时应力以及冷却后的残余应力都需要借助有限元计算程序来实现。在材料属性中,假设工件材料为各向同性。
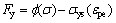 (12)
(12)
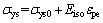 (13)
(13)
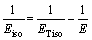 (14)
(14)
式中:Fy为材料屈服函数;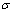 为应力;
为应力;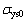 为初始屈服应力;
为初始屈服应力;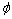 为加权函数;εpe为等效塑性应变;Eiso为各向同性硬化模量;E为弹性模量;ETiso为各向同性切线模量。
为加权函数;εpe为等效塑性应变;Eiso为各向同性硬化模量;E为弹性模量;ETiso为各向同性切线模量。
式(12)中屈服应力σys(εpe)取决于等效塑性应变εpe。由式(12)~(14)可以给出材料在塑性阶段塑性硬化对工件残余应力的影响。
当磨削时长t=2 s时,瞬时应力σx在工件表面上的分布情况见图9(a)。从图9(a)可见:随着热源在工件表面移动,在砂轮与工件接触区域产生瞬时压应力,热源流过的区域变为拉应力;随着温度降低,拉应力也缓慢降低。图9(b)所示为瞬时应力σx在磨削时间t= 2 s时沿垂直工件表面深度方向的变化情况。从图9(b)可见:随着深度增加,在表层以下开始,工件产生的瞬时应力σx的位置在水平方向上(x轴)滞后于热源位置,且随着深度增加,瞬时拉压应力下降。
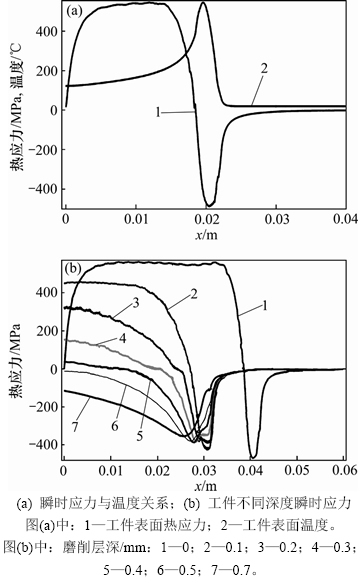
图9 热源移动过程中热应力变化
Fig. 9 Thermal stress changes during heat source movement
为了研究塑性开始产生时的温度阈值,将热源强度Q由大到小逐渐减小,得到工件材料内产生塑性变形的区域,如图10所示。从图10可见:随着热源强度Q减小,工件内产生等效塑性应变越来越小;当热源强度Q=55 W/mm2时,工件几乎不产生塑性变形,也就是说,热源强度为55 W/mm2和P=2为材料发生临界弹塑性变形的条件,由此可以得出影响工件开始产生热塑性形变的磨削条件曲线,如图11所示。根据有限元计算,当P从1~4之间变动时,材料产生临界热塑性变形对应的磨削区域最高温度在170~190 ℃之间波动。
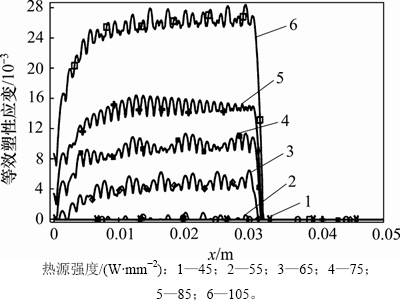
图10 等效热塑性应变
Fig. 10 Equivalent heat plastic strain
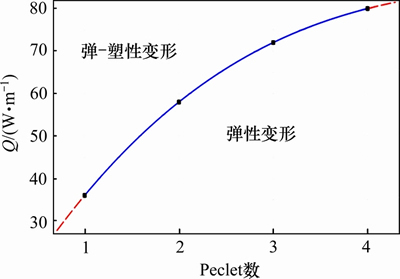
图11 初始热塑性应变与磨削条件的关系
Fig. 11 Relationship between onset heat plastic strain and grinding conditions
3 实验验证
3.1 温度磨削实验
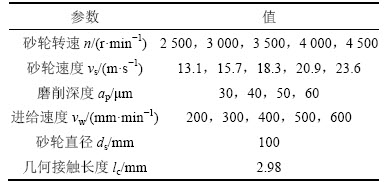
测量磨削温度最直接的方法是用热电偶测量磨削区温度,也就是将热电偶埋于表面下一定深度,通过缠有屏蔽线的热电偶延长线引入数据采集卡借口,利用采集软件进行数据采集,采样频率为250 kHz。当砂轮磨削到热电偶所在高度时,可以采集到磨削区最高温度,其原理如图12所示(测力仪为KISTLER 9257B,采样频率为30 kHz)。砂轮选用CBN砂轮,砂轮粒度为0.125 mm,具体参数见表1。在实验过程中不使用磨削液,即采用干磨削。磨削实验参数见表2。
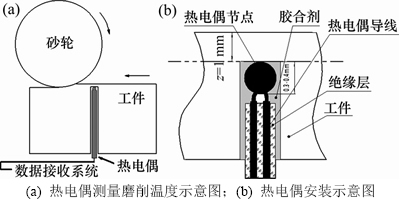
图12 热电偶测量温度原理图
Fig. 12 Schematic diagram of thermocouple temperature measurement
表2 干磨削状态下磨削工况参数
Table 2 Grinding parameters on dry grinding
3.2 残余应力测量
采用X线衍射法测量残余应力,该方法是目前测量残余应力最方便且高效的一种实验方法。此外,应用X线衍射法测量工件时不破坏工件,既能保证工件表层残余应力场的完整性,又能提高测试精度。所采用的残余应力测试仪器为PROTO公司的iXRD-300W便携式残余应力分析仪,该仪器满足最新的欧盟标准EN15305—2008和美国标准ASTM E915-10。采用完整应力方程和椭圆拟合方法,每点都能同时给出正应力和剪切应力。测量采用的衍射光栅直径为1 mm。残余应力测试点如图13所示。在工件表面取12个点,沿磨削方向进行测量。

图13 工件残余应力测量点位置
Fig. 13 Measuring positions of residual stress of work-piece
3.3 磨削温度计算值与实验室对比
当аp=30 μm,vw=200 mm/min时,磨削区域温度变化曲线如图14所示。从图14(a)可见:椭圆热源数值仿真结果与热电偶测量结果在磨削区域中温度上升阶段有良好的一致性;在温度下降过程中,磨削区域温度下降速度要小于仿真时的温度下降速度,这是由于在实验过程中,热电偶节点处被胶水包围,胶水热传导系数相对金属要小很多。在计算过程中,为了接近实际,在砂轮磨削过热电偶后,将热电偶附近材料热导率改为胶水热导率,其计算结果如图14(b)所示。从图14(b)可见:磨削区域温度下降速度与计算速度较吻合,磨削温度最大相对误差在5%以内。由以上分析可知:使用有限元仿真计算能准确得出磨削区域的温度变化历程。
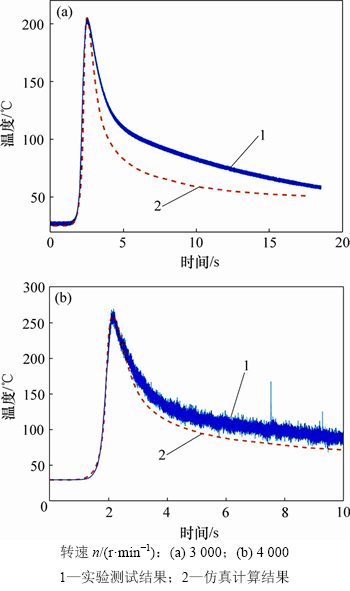
图14 аp=30 μm,vw=200 mm/min时,磨削区域温度变化曲线
Fig. 14 Temperature changed curves in grinding area when аp=30 μm and vw=200 mm/min
3.4 残余应力实验值与计算值对比
3.4.1 工件残余应力测量
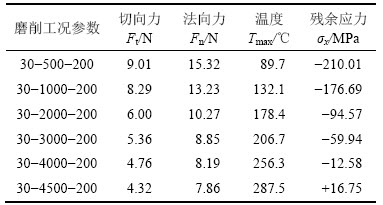
磨削后残余应力在表层有较大分散度,且在测量过程中存在误差干扰,通常测量误差在±20 MPa以内。为了减小误差,取工件上12个点进行测量,得出工件表层平均残余应力。本文中,测量工件上每个点的残余应力误差较小,误差范围在±10 MPa以内。在不同磨削参数下,磨削温度、磨削力及残余应力见表3,磨削工况参数编号如30-500-200表示磨削深度(аp)为30 μm,转速(n)为500 r/min,进给速度(vw)为200 mm/min(其余类推)。磨削力使用KISTLER 9257B进行测量。
表3 不同磨削参数下磨削力、磨削温度及残余应力
Table 3 Grinding force, grinding temperature and residual stress of different grinding parameters
3.4.2 热力耦合工件残余应力的计算
计算残余应力的热力耦合关系流程如图15所示。工件表层残余应力测量值与计算值对比见图16。从图16可见:工件表层残余应力测量值与计算值相对误差在±10 MPa内,表明通过磨削力及磨削热耦合作用下计算得到的工件表层残余应力能有效仿真实际磨削加工中工件表层残余应力。
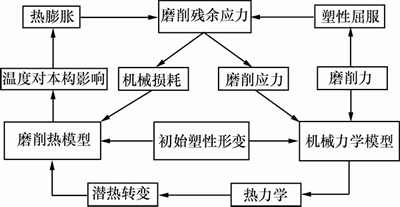
图15 计算残余应力的热力耦合关系图
Fig. 15 Diagram of thermal-mechanical couple impact on calculate residual stress
不同磨削参数下磨削表层残余应力计算值与实测值及磨削区域最高温度见表4。由于磨削表层残余应力主要是由磨削过程中磨削热产生的热应力及磨削力引起,磨削热使工件表层产生拉应力,而磨削机械力主要使工件表层产生压应力[4],当磨削区域温度达到一定值时,热应力对残余应力的影响大于机械力对残余应力的影响,使工件表层呈现残余拉应力。从表4可见:采用有限元计算得到的残余应力远远低于实测值,这是由于磨削过程中工件材料内部应力未达到初始屈服应力,机械力作用对残余应力作用影响较小。等温机械切削要使工件材料产生磨削初始塑性应变需要达到材料的初始屈服极限,而磨削过程中产生的应力由砂轮与工件接触产生的机械应力及热应力组成,在磨削温度未达到热塑性应变临界温度时,工件材料热膨胀产生弹性应变,耦合机械力后,机械力对工件残余应力场影响较小;当磨削温度超过热塑性应变临界温度时,工件产生塑性应变,机械力耦合塑性应变场,机械力对最终工件残余应力场产生较大作用。
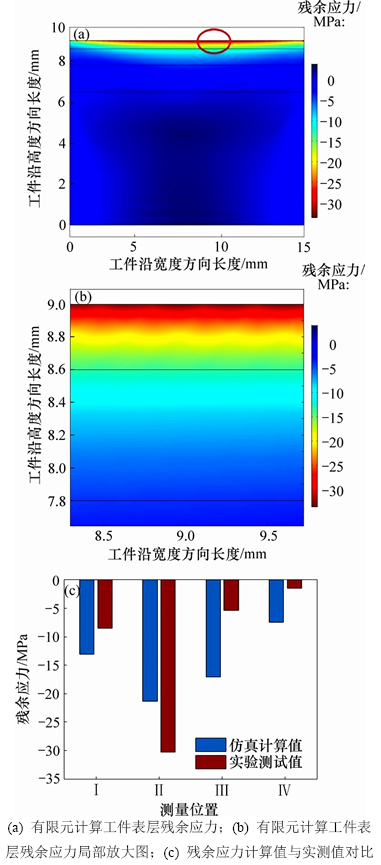
图16 n=4 000 r/min,аp=30 μm,vw=200 mm/min时,工件表层残余应力计算值与实测值对比
Fig. 16 Comparison of calculated value of residual stress and measured value when n=4 000 r/min, аp=30 μm and vw=200 mm/min
表4 不同磨削参数工件表层残余应力及磨削区域温度
Table 4 Surface residual stress and grinding zone temperature of different grinding parameters
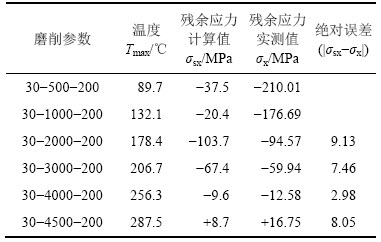
从表4还可见:在计算磨削残余应力中,由磨削温度产生的初始塑性应变对最终残余应力场有较大影响;在磨削区域最高温度达到170 ℃以上时,工件材料开始产生热塑性应变,在热力耦合作用下,工件表层残余应力计算值与实测值误差在±10 MPa之内。
通过实验研究及有限元对磨削表层残余应力的计算可以发现:当磨削参数一定时,仅改变砂轮转速便可以得出产生磨削残余拉应力的磨削温度阈值为275~285 ℃;在有限元中计算过程中,当温度达到178 ℃时,材料开始发生热塑性应变;当磨削区域温度为178.4 ℃时,实测残余应力与计算值的误差在允许范围之内;当磨削区域温度达170~190 ℃时,材料开始产生热塑性应变。
4 结论
1) 提出磨削过程中产生残余应力的温度阈值概念,给出残余应力产生的磨削参数临界条件计算方法,得到定量研究磨削过程中残余应力温度阈值计算公式。
2) 在磨削过程中,热应力随热源移动,沿深度方向拉应力逐渐减小,在2y/lc =0.4时开始产生压应力;磨削温度随工件磨削速度增大而增大,在170~190 ℃时开始产生塑性变形,此温度为产生残余拉应力的临界温度。
3) 通过埋热电偶测量实验磨削温度,得到了磨削过程中砂轮与工件接触区域磨削温度,有限元仿真结果与实验结果相对误差在5%以内,表明通过椭圆热源分布模型能较好的模拟磨削区域温度场。
4) 运用X线衍射仪对残余应力进行测量,得到工件表层残余应力;通过热力耦合方法所得工件表层磨削残余应力的计算结果与实测值相对误差在±10 MPa以内,表明使用有限元软件能有效计算磨削表层残余应力。在一定磨削参数下,平面磨削中产生残余拉应力的磨削区域温度阈值为275~285 ℃;在磨削过程中,12CrNi4A材料产生初始热塑性应变的温度为170~190 ℃。
参考文献:
[1] MISHRA A, PRASAD T. Residual stresses due to a moving heat source[J]. International Journal of Mechanical Sciences, 1985, 27(9): 571-581.
[2] BRINKSMEIER E, CAMMETT J T, K NIG W, et al. Residual stresses-measurement and causes in machining processes[J]. CIRP Annals: Manufacturing Technology, 1982, 31(2): 491-510.
NIG W, et al. Residual stresses-measurement and causes in machining processes[J]. CIRP Annals: Manufacturing Technology, 1982, 31(2): 491-510.
[3] DING Wenfeng, ZHANG Liangchi, LI Zheng, et al. Review on grinding-induced residual stresses in metallic materials[J]. International Journal of Advanced Manufacturing Technology, 2017, 88(9/10/11/12): 2939-2968.
[4] CHOI Y. A comparative study of residual stress distribution induced by hard machining versus grinding[J]. Tribology Letters, 2009, 36(3): 277-284.
[5] ZHANG Jianhua, GE Peiqi, JEN T C, et al. Experimental and numerical studies of AISI1020 steel in grind-hardening[J]. International Journal of Heat & Mass Transfer, 2009, 52(3/4): 787-795.
[6] AZARHOUSHANG B, DANESHI A, LEE D H. Evaluation of thermal damages and residual stresses in dry grinding by structured wheels[J]. Journal of Cleaner Production, 2017, 142(4): 1922-1930.
[7] GROVE T, LUCAS H, DENKENA B. Residual stresses in grinding of forming tools with toric grinding pins[J]. Procedia Cirp, 2018, 78: 354-357.
[8] BLOK H. Theoretical study of temperature rise at surfaces of actural contact under oiliness lubricating conditions[C]// Proceedings of the General Discussions on Lubrication. London, 1937: 222-35.
[9] JAEGER J C. Moving sources of heat and the temperature of sliding contacts[J]. Proceedings of the Royal Society of New South Wales, 1942, 76: 203-224.
[10] LI Haonan, AXINTE D. On a stochastically grain-discretized model for 2D/3D temperature mapping prediction in grinding[J]. International Journal of Machine Tools & Manufacture, 2017, 116: 60-76.
[11] POMBO I, S NCHEZ J A, ORTEGA N, et al. Contact length estimation in grinding using thermocouple measurement and numerical simulation[J]. International Journal of Advanced Manufacturing Technology, 2012, 59(1/2/3/4): 83-91.
NCHEZ J A, ORTEGA N, et al. Contact length estimation in grinding using thermocouple measurement and numerical simulation[J]. International Journal of Advanced Manufacturing Technology, 2012, 59(1/2/3/4): 83-91.
[12] MISHRA A, PRASAD T. Residual stresses due to a moving heat source[J]. International Journal of Mechanical Sciences, 1985, 27(9): 571-581.
[13] HAMDI H, ZAHOUANI H, BERGHEAU J M. Residual stresses computation in a grinding process[J]. Journal of Materials Processing Technology, 2004, 147(3): 277-285.
[14] SHAH S M, N LIAS D, ZAIN-UL-ABDEIN M, et al. Numerical simulation of grinding induced phase transformation and residual stresses in AISI-52100 steel[J]. Finite Elements in Analysis & Design, 2012, 61(6): 1-11.
LIAS D, ZAIN-UL-ABDEIN M, et al. Numerical simulation of grinding induced phase transformation and residual stresses in AISI-52100 steel[J]. Finite Elements in Analysis & Design, 2012, 61(6): 1-11.
[15] 张修铭, 刘莉娟, 修世超, 等. 基于热-力耦合磨削表层残余应力的仿真分析[J]. 东北大学学报(自然科学版), 2014, 35(12): 1758-1762.
ZHANG Xiuming, LIU Lijuan, XIU Shichao, et al. Simulation analysis of surface residual stress based on thermal-mechanical coupling[J]. Journal of Northeastern University(Science and Technology), 2014, 35(12): 1758-1762.
[16] CHEN Jianbin, FANG Qihong, ZHANG Liangchi. Investigate on distribution and scatter of surface residual stress in ultra-high speed grinding[J]. International Journal of Advanced Manufacturing Technology, 2014, 75(1/2/3/4): 615-627.
[17] 任敬心, 孟庆国, 陈景蕙. GH33A高温合金的磨削温度与残余应力[J]. 航空制造技术, 1995(1): 3-7.
REN Jingxin, MENG Qingguo, CHEN Jinghui. Grinding temperature and residual stress of GH33A superalloy[J]. Aviation Manufacturing Technology, 1995(1): 3-7.
[18] HOU Z B, KOMANDURI R. General solutions for stationary/moving plane heat source problems in manufacturing and tribology[J]. International Journal of Heat & Mass Transfer, 2000, 43(10): 1679-1698.
[19] ROWE W B. Thermal analysis of high efficiency deep grinding[J]. International Journal of Machine Tools & Manufacture, 2001, 41(1): 1-19.
[20] BATHE K J, KHOSHGOFTAAR M R. Finite element formulation and solution of nonlinear heat transfer[J]. Nuclear Engineering & Design, 1979, 51(3): 389-401.
[21] JONSSON M, JOSEFSON B L. Experimentally determinzed transient and residual stress in a butt-welded pipe[J]. The Journal of Strain Analysis for Engineering Design, 1988, 23(1): 25-31.
[22] WANG K F, CHANDRASEKAR S, YANG H T Y. An efficient 2D finite element procedure for the quenching analysis with phase change[J]. Journal of Engineering for Industry, 1993, 115(1): 121238.
[23] LEFEBVRE A, VIEVILLE P, LIPINSKI P, et al. Numerical analysis of grinding temperature measurement by the foil/workpiece thermocouple method[J]. International Journal of Machine Tools & Manufacture, 2006, 46(14): 1716-1726.
[24] BLOK H. The dissipation of frictional heat[J]. Applied Scientific Research, 1955, 5(2/3): 151-181.
(编辑 陈灿华)
收稿日期:2018-03-10;修回日期:2018-05-22
基金项目(Foundation item):国家自然科学基金资助项目(51535012,U1604255);湖南省重点研发计划项目(2016JC2001) (Projects(51535012, U1604255) supported by the National Natural Science Foundation of China; Project(2016JC2001) supported by Key Research and Development Program of Hunan Province)
通信作者:唐进元,博士,教授,从事复杂齿面制造、超声磨削表面完整性研究;E-mail: jytangcsu@163.com