Coupling effect of evaporation and condensation processes of organic Rankine cycle for geothermal power generation improvement
来源期刊:中南大学学报(英文版)2019年第12期
论文作者:李太禄 杨华 孟楠
文章页码:3372 - 3387
Key words:Organic Rankine cycle; geothermal power generation; coupling effect of evaporation and condensation; exergy analysis
Abstract: Organic Rankine cycle (ORC) is widely used for the low grade geothermal power generation. However, a large amount of irreversible loss results in poor technical and economic performance due to its poor matching between the heat source/sink and the working medium in the condenser and the evaporator. The condensing temperature, cooling water temperature difference and pinch point temperature difference are often fixed according to engineering experience. In order to optimize the ORC system comprehensively, the coupling effect of evaporation and condensation process was proposed in this paper. Based on the laws of thermodynamics, the energy analysis, exergy analysis and entropy analysis were adopted to investigate the ORC performance including net output power, thermal efficiency, exergy efficiency, thermal conductivity, irreversible loss, etc., using geothermal water at a temperature of 120℃ as the heat source and isobutane as the working fluid. The results show that there exists a pair of optimal evaporating temperature and condensing temperatures to maximize the system performance. The net power output and the system comprehensive performance achieve their highest values at the same evaporating temperature, but the system comprehensive performance corresponds to a lower condensing temperature than the net power output.
Cite this article as: YANG Hua, MENG Nan, LI Tai-lu. Coupling effect of evaporation and condensation processes of organic Rankine cycle for geothermal power generation improvement [J]. Journal of Central South University, 2019, 26(12): 3372-3387. DOI: https://doi.org/10.1007/s11771-019-4260-y.

J. Cent. South Univ. (2019) 26: 3372-3387
DOI: https://doi.org/10.1007/s11771-019-4260-y

YANG Hua(杨华), MENG Nan(孟楠), LI Tai-lu(李太禄)
School of Energy and Environmental Engineering, Hebei University of Technology,Tianjin 300401, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: Organic Rankine cycle (ORC) is widely used for the low grade geothermal power generation. However, a large amount of irreversible loss results in poor technical and economic performance due to its poor matching between the heat source/sink and the working medium in the condenser and the evaporator. The condensing temperature, cooling water temperature difference and pinch point temperature difference are often fixed according to engineering experience. In order to optimize the ORC system comprehensively, the coupling effect of evaporation and condensation process was proposed in this paper. Based on the laws of thermodynamics, the energy analysis, exergy analysis and entropy analysis were adopted to investigate the ORC performance including net output power, thermal efficiency, exergy efficiency, thermal conductivity, irreversible loss, etc., using geothermal water at a temperature of 120℃ as the heat source and isobutane as the working fluid. The results show that there exists a pair of optimal evaporating temperature and condensing temperatures to maximize the system performance. The net power output and the system comprehensive performance achieve their highest values at the same evaporating temperature, but the system comprehensive performance corresponds to a lower condensing temperature than the net power output.
Key words: Organic Rankine cycle; geothermal power generation; coupling effect of evaporation and condensation; exergy analysis
Cite this article as: YANG Hua, MENG Nan, LI Tai-lu. Coupling effect of evaporation and condensation processes of organic Rankine cycle for geothermal power generation improvement [J]. Journal of Central South University, 2019, 26(12): 3372-3387. DOI: https://doi.org/10.1007/s11771-019-4260-y.
1 Introduction
At present, the worsening climate and serious environmental pollution in the world make it urgent to change the energy structure and improve the use of energy [1, 2]. Due to the huge reserves of medium and low temperature heat energy in the world, it is widely distributed, including solar energy, ocean temperature difference energy, geothermal energy and industrial waste heat. Therefore, converting low-grade waste heat into convenient and flexible high-grade electric energy without consuming other fossil fuels is an effective way to improve energy efficiency and reduce environmental pollution [3]. As one of the promising technologies for power generation, the ORC is often selected [4-6]. PILI et al [7] argued that the organic Rankine cycle is useful in recovering available waste heat for power generation at medium temperature, but it must be traded off between reducing environmental impact and investment costs. CAVAZZINI et al [8] believed that organic Rankine cycle (ORC) provides a valuable alternative for the recovery of waste heat from internal combustion engines (ICE) in transport systems, thus saving fuel and reducing emissions.
In recent years, a large number of researchers have studied the ORC power generation performances driven by different heat sources [9, 10]. SUN et al [11] deduced and optimized the performance analysis function and exergy efficiency of the ORC in the ocean thermal energy conversion process. USTAOGLU et al [12] studied the power generation performance of the ORC system with industrial waste heat as the heat source. The recovery capacity of the ORC exhaust gas was evaluated, and the energy and energy properties of the isentropic and dry fluid were analyzed under different conditions. NI et al [13] proposed that power generation by coupling ORC with solar energy could reduce fossil fuel consumption and CO2 emissions. However, the intensity of solar radiation varies throughout the day, so the cloud blockage of the sun has a great impact on the normal operation of the ORC system. It can be seen that the most renewable energy sources are intermittent and non-programmable, failing to provide consistently stable heat supply, and there is no guarantee matching between the high energy production cycle and its needs [14]. Therefore, a lot of renewable resources are limited by their nature, but geothermal heat is the most reliable and stable. The medium-low temperature geothermal energy with temperature changes between 50 and 350 °C can be directly used in power plants for power generation. Due to the abundant and extensive geothermal reserves in the world, this resource has received great attention [15]. In recent years, more researchers have begun to use geothermal heat as a heat source to optimize the ORC system [16, 17].
The research on ORC technology mainly focuses on several main aspects such as system structure, parameter optimization and working quality matching analysis. In terms of structural optimization of the system, based on the ORC system configuration, MAGO et al [18] studied the exergetic loss of the ORC system and found that the enthalpy loss of the evaporator is far greater than the exergetic loss of other systems, accounting for about 77% of the system enthalpy loss. Subsequently, MAGO et al [19] proposed a regenerative organic Rankine cycle (RORC) based on ORC system, and compared the two. It was concluded that RORC could increase the specific enthalpy of working fluid at the entrance of evaporator so that the thermal efficiency of RORC was higher than that of ORC. However, TCHANCHE et al [20] found that the installation of regenerator did not play a significant role in isentropic refrigerants by analyzing the performance of different circulating refrigerants in ORC and RORC systems. Later, LI et al [21, 22] optimized RORC and proposed parallel double- evaporator regenerative organic Rankine cycle (PDRORC) and series double-evaporator regenerative organic Rankine cycle (SDRORC) on the basis of RORC. WANG et al [23] proposed a new combined power cooling system which combines organic Rankine cycle (ORC) with vapor compression refrigeration cycle (VCRC). The comparative study of the system form and cycle parameter optimization analysis of the three methods shows that SDORC has a higher degree of improvement in power generation performance than RORC and PDORC. While THIERRY et al [24] found that although the multi-stage configuration is effective, it is limited in cost compared with single-stage cycle through the optimization process of multi-stage organic Rankine cycle with mixture as working fluid. The multi-stage evaporation of ORC not only improves the evaporation efficiency of the system, but also deteriorates the expansion and condensation process of the system. Therefore, we mainly analyze and optimize the single-stage ORC system in this paper.
During the operation of the ORC power generation system, the matching between the working medium and the cold-heat source, the physical properties of the working medium are closely related to the operating efficiency and safety of the system. SALEH et al [25] conducted theoretical cycle performance analysis on the thermodynamic properties of 31 pure working fluids of ORC system based on the first law of thermodynamics and the second law, and found that the working temperature with relatively lower critical temperature is more excellent, for example, R143a and R152a. For the impact of ORC working fluids leakage, the use of lower GWP fluids can produce 50%-84% reductions [26]. LI et al [27] found that R601a and R601 can be used to replace R123 for power generation when geothermal water is below 110 °C. ALJUNDI [28] and YARI [29] found that hydrocarbons would be a potential working fluid for ORC thermoelectric conversion systems driven by low temperature heat sources compared to traditional organic working fluids. Then XU et al [30] showed that cyclohexane is most feasible in medium-low temperature geothermal power generation by comparing 11 kinds of working fluids. Subsequently, in order to better match the working fluid with the heat source and the evaporator, the researchers began to optimize the ORC using the zeotropic mixture working fluids. LIU et al [31] found that the ORC using R600a/R601 was 4%-7% higher than the ORC using pure R600a, and found that there is an optimum working fluid mole fraction when the cooling water temperature increases more than the condensation temperature slip [32].
For optimization of system parameters, HU et al [33] found that the heat transfer coefficient in a brazed plate heat exchanger (BPHE) for organic Rankine cycle (ORC) is highly sensitive to heat flux and mass flow of working fluid. SUN et al [34] optimized the pinch point temperature difference (PPTD) between the evaporator of system and found that the leveling power cost (LCOE) and dynamic payback period (PBP) of the ORC are minimized when the evaporator PPTD is about 7 °C. OZDIL et al [35] studied the influence of different water phase calculation components on the system performance on the basis of optimizing the system PPTD. It was found that the net output power of the system gradually increased with the dryness of the inlet water of the evaporator. ZHAO et al [36] believed that the back pressure of the ORC system engine increased and the output power gradually decreased as the cooling water inlet temperature increased. XU et al [37] considered that evaporation and condensation temperatures had a great influence on the thermal performance and net output power of regenerated organic Rankine cycle (RORC). It was also found that the condensation temperature has a more significant effect on the thermal performance of RORC because it affected the inlet liquid parameters of the ejector.
From previous studies, it can be seen that in order to reduce the irreversible loss of the ORC system and improve the power generation performance and thermal efficiency, most of these researchers focus on the matching of evaporation side and heat source, or isolate the condenser from the evaporator for analysis which does not allow the system to be fully optimized. However, as the part that affects the thermal efficiency and exergetic efficiency of the ORC system, the evaporator and condenser need to be coupled. For this reason, the evaporation-condensation coupling effect is proposed to analyze the optimal operation of the ORC system. While studying system parameters, structure, and matching between working fluids and systems, the selection of objective functions is also important for system. In this paper, the evaporating- condensing coupling effect is used to analyze Wnet, ηth, ηex, I, KA, VFR, SP, fobj. From this, the optimal evaporating-condensing coupling temperature, the cooling water temperature difference and the pinch point temperature difference can be obtained to improve the thermodynamic and economic performance of the ORC system.
2 Analysis of an ORC system
Figure 1 shows that the ORC system is composed of main components such as evaporator, condenser, steam turbine, and working fluid pump. The cycle mechanism of the medium-low temperature thermoelectric conversion ORC system is similar to the cycle mechanism of the Rankine cycle. The main working flow is as follows: The low-temperature and low-pressure organic working fluid flows into the evaporator after being pressurized by the working fluid pump (Figure 1, state point 5; Figure 2 process 4-5), and undergoes a phase change after being heat-exchanged with the heat source reversely flowing through the evaporator (Figure 1, state point 1; Figure 2 process 6-1), so that the low-temperature and low-pressure liquid organic working fluid becomes saturated gaseous organic working fluid (Figure 2, state point 1). After that, it enters the steam turbine to expand and does work (Figure 1, state point 2; Figure 2 process 1-2), at this time, the heat energy carried by the working fluid is converted into shaft power to drive the steam turbine to work to generate electricity. After the work, the low pressure working fluid flowed from the steam turbine into the condenser, and converted into a saturated liquid organic medium by heat exchange with the cooling water flowing backwards through the condenser (Figure 1, state point 4; Figure 2 process 2-4), then it again flowed into the working fluid pump to complete one cycle (Figure 1, state point 5; Figure 2 process 4-5).
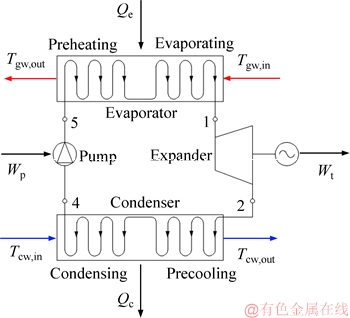
Figure 1 Schematic diagram of ORC system
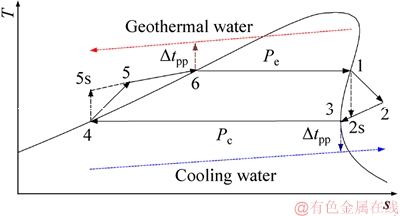
Figure 2 T-s schematic diagram of an ORC system
3 Mathematical model
3.1 Assumptions
According to the first law of thermodynamics and the second law, the mathematical model of each part of the system is established. To facilitate the establishment of the mathematical model and to simplify the analysis, the following assumptions are made:
1) The three systems of cold and heat sources and the various components of the system operate in steady state;
2) The pinch point temperature difference is the same at the heat source and the cold source;
3) Changes in kinetic and potential energy of organic working fluids in the system are ignored;
4) The pressure drop and friction loss of organic working fluids in evaporators, condensers and pipes, as well as heat losses in pipes are ignored;
5) Energy loss during mixing of organic media in steam turbines is ignored.
3.2 Governing equation
The mathematical model equations for each part of the ORC system are as follows:
Evaporator:
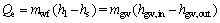 (1)
(1)
where Q, m and h denote the thermal load, the mass flow rate and the specific enthalpy; subscripts e, wf and gw stand for the evaporator, the working fluid and the geothermal water respectively; the subscripts in and out denote the inlet and outlet of evaporator.
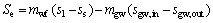 (2)
(2)
where △s and s mean the entropy production and the specific entropy.
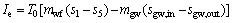 (3)
(3)
where I and T0 stand for the irreversible loss and the ambient temperature, respectively.
Pre-heating section:
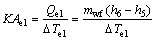 (4)
(4)
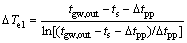 (5)
(5)
Evaporating section:
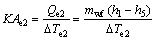 (6)
(6)
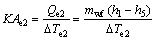 (7)
(7)
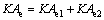 (8)
(8)
where subscripts e1 and e2 stand for the pre-heating and evaporating; KA stands for the thermal conductivity; △T and △tpp stand for the average temperature difference of heat exchanger and the pinch point temperature difference, respectively.
Turbine:
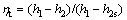 (9)
(9)
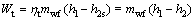 (10)
(10)
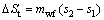 (11)
(11)
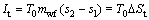 (12)
(12)
where η and W mean the efficiency and the power, respectively; t stands for turbine.
Condenser:
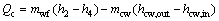 (13)
(13)
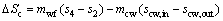 (14)
(14)
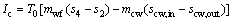 (15)
(15)
where subscripts c and cw stand for the condenser and cooling water, respectively.
Pre-cooling section:
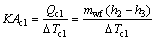 (16)
(16)
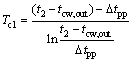 (17)
(17)
Condensing section:
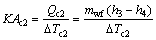 (18)
(18)
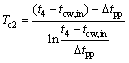 (19)
(19)
 (20)
(20)
where subscripts c1 and c2 stand for the pre-cooling and condensing.
Working fluid pump:
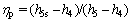 (21)
(21)
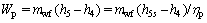 (22)
(22)
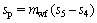 (23)
(23)
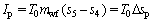 (24)
(24)
where subscript p stands for the working fluid pump.
Geothermal water pump:
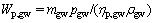 (25)
(25)
The energy consumption of heat source absorbed by geothermal drive wells is neglected here, while the process of geothermal water from wellhead to the use point of the system is pressurized by geothermal pump.
Cooling water pump:
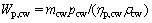 (26)
(26)
where p, η and ρ stand for pressure, efficiency and density, subscript p stands for pump.
The mass flow of organic working fluid:
 (27)
(27)
The mass flow of cooling water:
 (28)
(28)
Net power output:
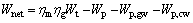 (29)
(29)
where Wnet is the net power output; ηm and ηg are the mechanical efficiency and power generation efficiency of the turbine, respectively.
Thermal efficiency:
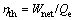 (30)
(30)
Exergetic efficiency:
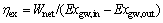 (31)
(31)
Total entropy production:
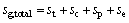
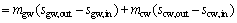 (32)
(32)
Total irreversible loss:
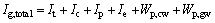 (33)
(33)
Total thermal conductance:
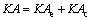 (34)
(34)
4 Validation
The correctness of the thermodynamic model is verified by comparison with the actual ORC device parameters of the geothermal power plant in the oil field [33]. The initial parameters are set to be the same as the geothermal power plant, and then the thermodynamic parameters are simulated. It can be seen from Table 1 that the theoretical simulation is in good agreement with the actual geothermal power generation data. The actual net output power of the power plant is 270 kW, the thermal efficiency is 3.96%, and the simulation results of net output power and thermal efficiency are increased by about 5.2% compared with the experiment; the VFR in the simulation results is about 13.7% higher than the actual power plant. The net output power, thermal efficiency and VFR of the system in the simulation results are higher than those in the actual power plant because the pressure drop and friction loss of organic working fluids in evaporator, condenser and pipeline, as well as the heat loss in pipeline are neglected in the theoretical model. Furthermore, the pure vacation of the working fluid in the theoretical model is set at 100%, while the purity of the working fluid in the actual geothermal power plant is 95%. Thereby, the reliability of the thermodynamic model can be verified.
Table 1 Validation of numerical model with previous published data [33] of an ORC

Table 2 Thermodynamic properties of isobutene

5 Results and discussion
5.1 Impact of cooling water temperature difference
For ORC, the simulation process combined with the mathematical model of the system can be obtained that the evaporation temperature is an independent variable which is the basic parameter of the entire system. On the other hand, the influence of inlet and outlet temperature difference of cooling water as well as the condensing temperature and the pinch point temperature difference on the power generation performance is discussed, the evaporating-condensing coupling effects are analyzed to get the best operating conditions of the system. In this section, isobutane is used as the working medium, and the optimal te and △tcw are studied at a fixed heat source inlet temperature tgw of 120 °C, the condensing temperature tc of 35 °C and the pinch point temperature difference Δtpp is 10 °C.
Figure 3 shows the effect of the evaporation temperature and the temperature difference of the cooling water on the net power output of the system at tgw,in=120 °C, tc=35 °C. Clearly, the net power output of the ORC system increases first and then decreases with the evaporation temperature, and there is an optimal evaporation temperature to maximize the net power output. From Eq. (29), we can see that the net power output Wnet is related with the turbine output power of the system Wt, the power consumed by the working medium pump Wp, the power consumed by the cooling pump Wp,cw, and the power consumed by the hot water pump Wp,hw. Since the value of power output of the turbine is much larger than that of cold and hot water pumps and working fluid pumps, the net output power Wnet is approximately consistent with the output power of steam turbines Wt. From Eq. (10), the output power of the turbine Wt is related to the mass flow rate of the working medium mwf and the specific enthalpy drop of the working fluid at the inlet and outlet of the steam turbine. With the increase of the evaporation temperature, the mass flow rate of the working fluid in the ORC system is reduced, but its specific enthalpy drop is increased. Therefore, when the evaporation temperature is 76 °C, the product of the two parameters reaches the maximum value; According to Eqs. (26) and (28), the power consumed by the cooling water pump Wp,cw is proportional to the mass flow rate of the cooling water mcw, which is inversely proportional to the temperature difference of the cooling water △tcw under the same cooling load. When the temperature difference of the cooling water △tcw reaches the maximum, as Δtcw=10 °C, the power consumed by the cooling water pump Wp,cw is the smallest; the net power output Wnet reaches the maximum. Therefore, the net power output of the system changes from 10.43 to 12.33 kW, when the evaporation temperature te is 76 °C and the temperature difference of cooling water △tcw is 10 °C, the net power output has a maximum value of 12.33 kW.
Figure 4 illustrates that thermal efficiency ηth changes with evaporating temperature te and temperature difference of cooling water △tcw. It can be seen that the thermal efficiency ηth increases with the evaporation temperature te and reaches a maximum at the evaporation temperature of 106 °C. From Eq. (30), we can see that the thermal efficiency ηth is proportional to the net output power Wnet of the system and inversely proportional to the heat transferred from the heat source to the working fluid Qe. It is known that the condensation temperature tc is fixed, when the evaporation temperature increases, the net output power Wnet of the system increases due to the enthalpy difference between the inlet and outlet of the working fluid pump increases, and the heat transferred from the heat source to the working medium Qe decreases due to the increase of the enthalpy at the inlet of the evaporator. Therefore, the thermal efficiency ηth of the system gradually increases. According to Eqs. (26), (28) and (30), the power consumption of the cooling water pump Wp,cw decreases with the increase of the temperature difference of the cooling water △tcw, so that the net output power of the system Wnet increased, therefore, the thermal efficiency ηth is gradually increases and when the temperature difference of the cooling water △tcw is 10 °C, the maximum value is reached. In summary, the thermal efficiency ηth of the system changes from 5.1% to 16.6%, and the optimum condition for thermal efficiency ηth is 16.6% at te=106 °C and Δtcw=10 °C.
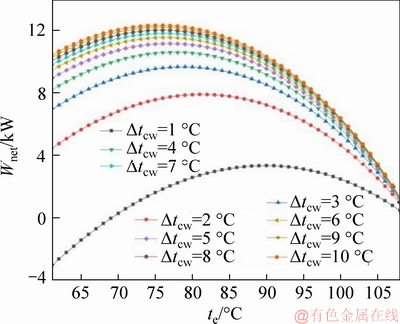
Figure 3 Net power output with evaporating temperature and temperature difference of cooling water at a fixed condensing temperature of 35 °C
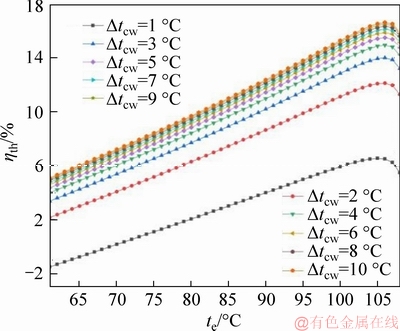
Figure 4 Thermal efficiency with evaporating temperature and temperature difference of cooling water at a fixed condensing temperature of 35 °C
Figure 5 shows the exergetic efficiency ηex with evaporating temperature te and temperature difference of cooling water △tcw at tc=35 °C. As the evaporation temperature te increases, the exergetic efficiency ηex tends to increase first and then decrease and reaches the maximum when the evaporation temperature te is 99 °C. From Eq. (30), we can see the same rules as the thermal efficiency ηth that is proportional to the net output power Wnet of the system and inversely proportional to the heat transferred from the heat source to the working fluid Qe. However, the exergetic efficiency ηex of the system is not only inversely proportional to the heat obtained from the heat source, but also related to the heat loss between the heat source and the environment during the heat exchange process. Therefore, there is a turning point in the exergetic efficiency ηex of the ORC. According to Eqs. (26), (28) and (31), the same as the law of thermal efficiency ηth, when the temperature difference of the cooling water △tcw reaches the maximum, as Δtcw=10 °C, the exergetic efficiency reaches the maximum. In conclusion, the exergetic efficiency ηex of the system changes from 21.4% to 34.5%, when the evaporation temperature te is 99 °C and the cooling water temperature difference Δtcw is 10 °C, the thermal efficiency ηex reaches the best value of 34.5%.
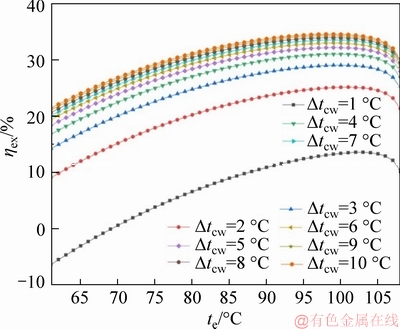
Figure 5 Exergetic efficiency with evaporating temperature and temperature difference of cooling water at a fixed condensing temperature of 35 °C
Figure 6 depicts when the heat source temperature tgw,in is 120 °C and the condensing temperature tc is 35 °C, the irreversible loss of the system Ig,total changes with the evaporation temperature te. Clearly, as the evaporation temperature te increases, the irreversible loss Ig,total tends to be decreased. It can be seen from Eq. (33) that the irreversible loss Ig,total is composed of four parts: the irreversible loss of the evaporator Ie, the irreversible loss of the steam turbine It, the irreversible loss of the condenser Ic and the irreversible loss of the working fluid pump Ip. According to Eqs. (3), (12), (15) and (24), the irreversible loss of each part of the system is proportional to the mass flow of the working fluid mwf. Since the mass flow of the working fluid mwf gradually decreases with the increase of the evaporation temperature, the irreversible loss Ig,total gradually decreases. Therefore, when the evaporation temperature te is maximum, te=109 °C, the irreversible loss Ig,total is minimum. From Eqs. (26) and (28), we can see that the power consumed by the cooling water pump Wp,cw is inversely proportional to the temperature difference of the cooling water △tcw. According to Eq. (33), when the temperature difference of the cooling water △tcw increases, the cooling pump consumes more power, so the irreversible loss Ig,total increases and it is minimum when △tcw=10 °C. In summary,the irreversible loss of the system changes Ig,total from 28.03 to 1.26 kW, and the minimum irreversible loss Ig,total condition is 1.26 kW at te=109 °C and Δtcw=10 °C.
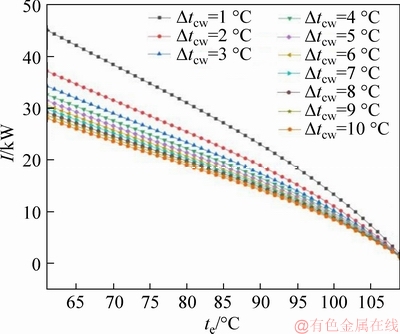
Figure 6 Irreversible loss of the system with evaporating temperature and temperature difference of cooling water at a fixed condensing temperature of 35℃
Figure 7 illustrates that with the increase of evaporation temperature (te), the thermal conductivity of the ORC system KA shows a decreasing trend. The thermal conductivity KA consists of the evaporator thermal conductivity (KA)e and the condenser thermal conductivity (KA)c defined in Eq. (34). Combining Eqs. (4) and (6), we can see that the thermal conductivity KA of the system is proportional to the amount of heat transfer Qe and inversely proportional to the logarithmic mean temperature difference △T. Among them, as te increases, the mass flow rate mwf of the ORC system is reduced, so that the heat transfer Qe between the heat source and the working medium is also reduced, resulting in a decrease in the thermal conductivity of the system KA. From Eqs. (18), (19), it can be seen that the temperature difference of the cooling water △tcw is proportional to the logarithmic mean temperature difference △T and inversely proportional to the thermal conductivity (KA)c of the condenser. Therefore, when the temperature difference of the cooling △tcw water is 10 °C, the thermal conductivity KA of the system is the largest. In conclusion, as the temperature difference of the cooling water △tcw increases, the range of thermal conductivity KA changes from 35.45 to 61.86 kW/°C and reaches an optimum value of 61.86 kW/°C under the condition of △te=109 °C and △tcw=10 °C.
In this work, the volumetric flow ratio (VFR, Rvf) and size parameter (SP, Ps) of turbine are used as indicators to evaluate the cost of the turbine in the system. The definitions of Rvf and Ps are as follows:
Rvf=Vout/Vin (35)
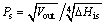 (36)
(36)
where V and ΔH are the volume flow and specific enthalpy difference, subscripts in and out stand for steam turbine inlet and outlet, subscript is stand for isentropic process.
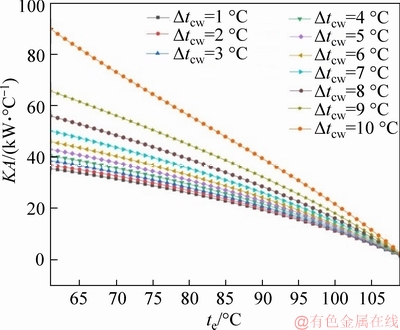
Figure 7 Thermal conductivity of system with evaporating temperature and temperature difference of cooling water at fixed condensing temperature of 35 °C
Figure 8 shows that with the increase of evaporation temperature te, the expansion ratio Rvf and the size parameters Ps of the turbine show an increasing and decreasing trend, respectively. It can be seen from Eq. (35) that the expansion ratio of the system is related to the volume flow of the working fluid at the inlet Vin and outlet Vout of the steam turbine, that is related to the evaporation temperature te and the condensation temperature tc. Therefore, when the condensation temperature tc is constant, the expansion ratio of the turbine with the evaporation temperature te increases. From Eq. (36), the size parameters of turbine is related to the volumetric flow rate of the working fluid at the outlet of the steam turbine Vout and its specific enthalpy difference ΔHis in the inlet and outlet of the turbine under the isentropic process. The enthalpy at the inlet of the evaporator h5 increases with the evaporation temperature te which is the main reason for the increase of the size parameter of the turbine in the ORC system. Therefore, when the evaporation temperature te is 109 °C, the expansion ratio and size parameter of the steam turbine are the maximum value of 6.42 and minimum value of 0.04 m, respectively.
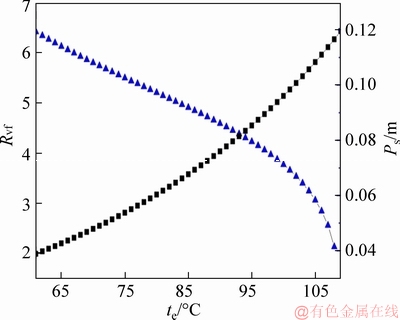
Figure 8 Expansion ratio and size parameter of turbine with evaporating temperature and temperature difference of cooling water at fixed condensing temperature of 35 °C
Combined with the research status at home and abroad, it can be seen that the research on the ORC system mainly focuses on improving the operating efficiency of various components of the system. In the above contents, the net output power Wnet, thermal efficiency ηth and exergetic efficiency ηex of the system are taken as objective functions respectively to compare and analyze the system. However, there is no recognized objective function for measuring the comprehensive performance of the ORC system. Based on this, a new objective function fobj is proposed to measure the economic performance of the ORC system. Among them, the net output power Wnet of the system represents the return rate of the system, while the parameter heat conductivity represents the input cost of the heat exchanger components, and the expansion ratio and size parameters of the steam turbine represent the input cost of the steam turbine in the system. Therefore, the larger the objective function is, the better the comprehensive performance of the system will be. The formula is as follows:
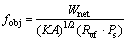 (37)
(37)
Figure 9 illustrates that the overall trend of the objective function fobj is generally consistent with the net output power Wnet of the system, that is, it increases first and then decreases with the evaporation temperature te, and there is an optimal evaporation temperature te to maximize the objective fobj. It also has the same trend with the temperature difference of the cooling water △tcw. Overall, the objective function fobj achieves an optimum value at te=83 °C, △tcw=5 °C, while the net output power Wnet is at te=76 °C, △tcw=10 °C to an optimum value. It can be seen that the net output power Wnet does not represent the comprehensive performance of the system.

Figure 9 Objective function with evaporating temperature and temperature difference of cooling water at a fixed condensing temperature of 35 °C
5.2 Impact of condensing temperature
This section focuses on the optimum evaporating temperature te and condensing temperature tc when the heat source temperature tgw is fixed at 120 °C, the cooling water temperature difference △tcw and the pinch temperature difference △tpp are 10 °C, respectively. It is used to discuss the evaporating-condensing coupling effect and to make the system in optimal operating conditions.
Figure 10 depicts the variation of the net output power Wnet of the system with evaporation temperature te and condensation temperature tc. It can be seen from the figure that the net output power Wnet increases first and then decreases with the evaporation temperature te, and reaches the optimum value when te=76 °C, which is the same as the change rule in the previous section. When the evaporation temperature te is constant, the net output power Wnet of the system increases as the condensation temperature tc decreases. It can be seen from Eqs. (10) and (29) that when the condensing temperature tc is reduced, the mass flow rate of the working medium mwf remains but the enthalpy difference of the steam turbine inlet and outlet increases, so that the net output power Wnet of the system is uniformly increased. Therefore, as the condensing temperature tc decreases, the optimal net output power Wnet of the system changes from 8.65 to 12.33 kW, and the best net output power Wnet of the system is under the conditions of te=76 °C, tc=35 °C.
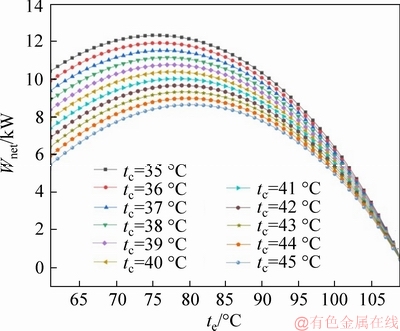
Figure 10 Net power output with evaporating temperature and condensing temperature at cooling water temperature difference of 10 °C
Figure 11 shows that thermal efficiency ηth gradually increases with evaporation temperature te. When the condensing temperature tc is fixed, with the increase of evaporation temperature te, the net output power Wnet of the system and the heat exchange between the heat source and working fluid Qe increase and decrease, respectively, by Eq.(30) it can be seen that the thermal efficiency ηth gradually increases. When the evaporation temperature te is constant and the condensation temperature tc is gradually decreased. It is known that the net output power Wnet of the system gradually increases and the heat exchange between the working medium and the heat source Qe does not change, resulting in a gradual increase in thermal efficiency ηth. When the evaporation temperature te reaches the optimum value, the thermal efficiency ηth of the system increases from 12.94% to 16.62% with the condensation temperature tc. In conclusion, the thermal efficiency ηth achieves the best value under the condition of te=106 °C, tc=35 °C.
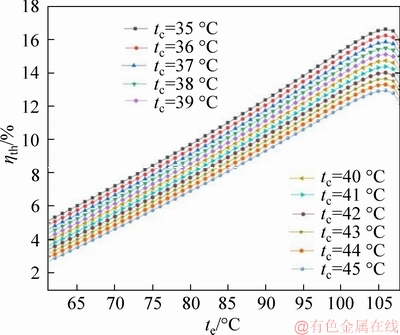
Figure 11 Thermal efficiency with evaporating temperature and condensing temperature at cooling water temperature difference of 10 °C
Figure 12 shows that the exergetic efficiency ηex of the system varies with evaporation temperature te which is the same as described in the previous section. As the evaporation temperature increases, the exergetic efficiency ηex tends to increase first and then decrease, and reaches the maximum when the evaporation temperature te is 99 °C. When the evaporation temperature te is fixed, the exergetic efficiency ηex of the system increases with decreasing condensation temperature tc. It can be proved by Eq. (31) that the net output power Wnet increases uniformly as the condensation temperature tc decreases, resulting in a uniform increase in the exergetic efficiency ηex of the system. Therefore, as the condensing temperature tc decreases, the optimal exergetic efficiency ηex of the system changes from 28.53 to 34.52 kW, and the best exergetic ηex efficiency of the system is under the conditions of te=99 °C, tc=35 °C.
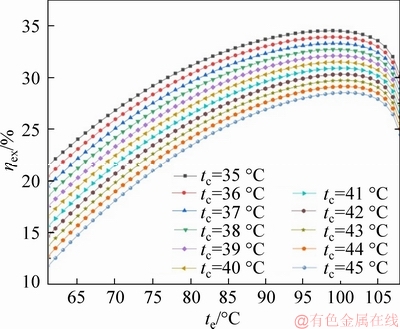
Figure 12 Exergetic efficiency with evaporating temperature and condensing temperature at cooling water temperature difference of 10 °C
From the previous part, it can be concluded that the optimal value of the objective function fobj is the largest when the temperature difference of the cooling water is 5 °C. Therefore, it can be seen from Figure 13 that under this condition the objective function fobj used to measure the overall performance of the ORC system increases first and then decreases with evaporation temperature teand reaches its optimum value at an evaporation temperature te of 85 °C. It can also be seen from the Figure 13 that as the condensing temperature tc increases, the objective function fobj value becomes larger and larger and reaches the maximum value at 44 °C. Therefore, under the condition of te=85 °C, tc=40 °C, △tpp=10 °C, the objective function fobj achieves an optimum value of 2.85.
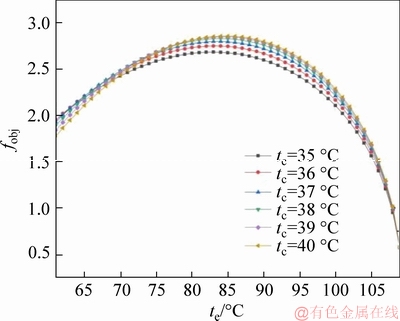
Figure 13 Objective function with evaporating temperature and condensing temperature at cooling water temperature difference is 5 °C
5.3 Impact of pinch point temperature difference
In the case of a certain heat source temperature tgw, in addition to the evaporation temperature te, the condensation temperature tc and the temperature difference of the cooling water △tcw will affect the performance of the ORC system, the pinch point temperature difference △tpp is also a very important factor. In this part, the influence of pinch point temperature difference △tpp on system performance is mainly studied at tc=35 °C, △tcw =10 °C.
Figure 14 illustrates that the pinch temperature difference △tpp is inversely proportional to the net output power Wnet of the system. According to Eq. (27), the net output power Wnet of the system is higher and higher because of the decrease of the pinch point temperature difference △tpp leads to an increase in the mass flow rate of the working medium mwf. It can be seen that the maximum value of net output power Wnet increases from 12.33 to 15.88 kW, and get the best value under the condition of te=81 °C, △tpp =1 °C.

Figure 14 Net power output with evaporating temperature and pinch point temperature difference at a fixed condensing temperature of 35 °C
According to Figure 15, the variation of the comprehensive performance of the ORC system with the temperature difference of the pinch point △tpp can be seen. The objective function fobj increases first and then decreases with the decrease of the temperature difference of the pinch point △tpp, and reaches the optimum value at △tpp=3 °C. Therefore, it can be seen that the ORC system achieves the best performance when the evaporation temperature te is 88 °C and the pinch point temperature difference △tpp is 3 °C. The variation of the maximum value of the objective function fobj with the condensing temperature tc and the cooling water temperature difference △tcw under this condition is shown in Table 3.
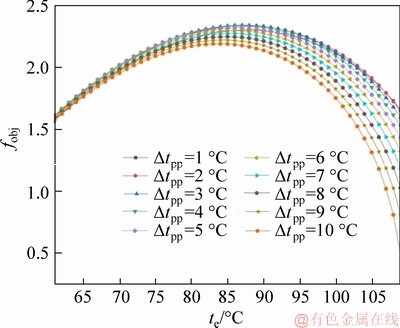
Figure 15 Objective function with evaporating temperature and pinch point temperature difference at a fixed condensing temperature of 40 °C
It can be seen from Table 3 and Figure 13 that when the pinch point temperature difference △tpp is 3 °C, the temperature difference of the cooling water △tcw is 10 °C, and the value of the objective function fobj is the largest at tc=38 °C, △tcw=10 °C, but less than the objective function fobj when the temperature difference of the cooling water △tcw is fixed at 5 °C. Therefore, the operating condition for achieving the optimization of the objective function fobj is te=85 °C, △tcw=5 °C, tc=40 °C.
The values of the parameters under the optimal conditions of net power output and comprehensive performance of the system are shown in Tables 4 and 5, respectively.
5.3 Comparison of optimum working conditions among different working fluids
In order to prove the universal applicability of the simulation results, the working conditions of different alkane refrigerants at the best net output power and comprehensive performance of the system are compared based on the coupling effect of condensation and evaporation. The comparison results and the values of each parameter are listed in Tables 6 and 7. It can be seen from the table that the working conditions of each alkane working fluid are basically the same when it achieves the best net output power and the best comprehensive performance. Only the evaporation temperature is slightly different, the net output power of each working fluid is the largest when the evaporation temperature is from 75 to 81 °C, and the comprehensive performance of the system corresponding to each working fluid is the best when the evaporation temperature is from 85 to 88 °C.
Table 3 Maximum objective function at te=88 °C
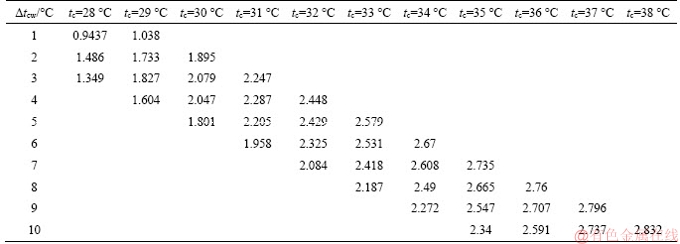
Table 4 System parameter values under optimal net power output

Table 5 System parameter values under optimal comprehensive performance

Table 6 System parameters corresponding to different working fluids under optimal net power output

Table7 System parameters corresponding to different working fluids under optimal comprehensive performance
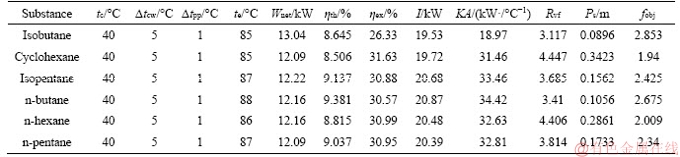
It can also be seen that the performance of isobutane is the best of all alkanes, regardless of the net output power or comprehensive performance of the system. Therefore, isobutane is recommended as the circulating working fluid of the system.
6 Conclusions
The organic Rankine cycle (ORC) is an efficient technology for low-medium geothermal power generation. The coupling effects between the evaporation and condensation processes are investigated. The main research conclusions are summarized as follows:
1) There exists a pair of evaporation temperature (81 °C) and condensation temperature (35 °C) to maximize the net power output(15.88 kW).
2) The working conditions corresponding to the optimal net power output and the optimal comprehensive system performance are different at the same evaporating temperature but different condensing temperatures. The condensing temperature for the optimal comprehensive system performance is 5 °C lower than that for the optimal net power output.
3) For each thermodynamic parameter, thermal efficiency, exergy efficiency and thermal conductivity vary with condensation temperature, cooling water temperature difference and pinch point temperature difference are basically the same, but with evaporation temperature change law is quite different. Among them, thermal efficiency and exergy efficiency are proportional to evaporation temperature, but the irreversible loss and thermal conductivity are inversely proportional to it.
4) The size parameters and expansion ratio of steam turbines vary inversely with evaporation temperature, so the matching of size parameters and expansion ratio has a great influence on the comprehensive performance of the system.
5) Overall, the cooling water temperature difference is proportional to the net output power, but the pinch point temperature difference is inversely proportional to the net output power. Therefore, a high cooling water temperature difference and a low pinch point temperature difference corresponds to high net power output. However, considering the comprehensive performance, the optimal cooling water temperature difference is 5 °C, and the pinch point temperature difference is 10 °C.
Nomenclatures
A
Area, m2
c
Specific heat, kJ/kg
Ex
Exergy, kW
h
Specific enthalpy, kJ/kg
I
Irreversibility rate, kW
K
Heat transfer coefficient, W/(m2·°C)
M
Molar mass, kg/kmol
m
Mass flow rate, kg/s
P
Pressure, MPa
Q
Heat transfer rate, kW
s
Specific entropy, kJ/(kg·°C)
T
Temperature, K
t
Temperature, °C
U
Intrinsic energy, kJ
W
Power, kW
ΔP
Pressure difference, Pa
fobj
Objective function
Greek symbols
η
Efficiency, %
ρ
Density, kg/m3
Ф
Entransy dissipation, kW/K
Subscripts
c
Condenser
cri
Critical
cw
Cooling water
e
Evaporator
ex
Exergetic
g
Generator
gw
Geothermal water
net
Net output
m
Mechanical
opt
Optimal
p
Pump
pp
Pinch point
s
Isentropic
t
Turbine
th
Thermal
wf
Working fluid
0
Environment
1, 2, 3, 4,
5, 6, 2s, 5s
State points
Acronyms
BPHE
Brazed plate heat exchanger
ICE
Internal combustion engines
LCOE
Leveling electricity of cost
ORC
Organic Rankine cycle
PBP
Payback period
PDRORC
Parallel double-evaporator regenerative
organic Rankine cycle
PPTD
Pinch point temperature difference
PTORC
Parallel two-stage organic Rankine cycle
RORC
Regenerative organic Rankine cycle
SP
Size parameters
SDRORC
Series double-evaporator regenerative organic Rankine cycle
STORC
Series two-stage organic Rankine cycle
VFR
Volumetric flow ratio
References
[1] GONZALEZ J E, MONCEF K. Handbook of integrated and sustainable buildings equipment and systems, volume I: Energy systems [M]. American Society of Mechanical Engineers, 2017.
[2] LI Gang, HWANG Y, RADERMACHER R. Cold thermal energy storage materials and applications toward sustainability [M]// Energy Solutions to Combat Global Warming. Springer, Cham, 2017.
[3] LI Gang, ZHENG Xue-fei. Thermal energy storage system integration forms for a sustainable future [J]. Renewable and Sustainable Energy Reviews, 2016, 62: 736-757.
[4] LIU Ke-tao, ZHU Jia-ling, HU Kai-yong, WU Xiu-jie. Analysis on optimal working fluid flow rate and unstable power generation for miniaturized ORC systems [J]. Journal of Central South University, 2016, 23(5): 1224-1231.
[5] LIU, Chang-wei, GAO Tie-yu. Off-design performance analysis of basic ORC, ORC using zeotropic mixtures and composition-adjustable ORC under optimal control strategy [J]. Energy, 2019, 171: 95-108.
[6] KONG R, DEETHAYAT T, ASANAKHAM A, VORAYOS N, KIATSIRIROAT T. Thermodynamic performance analysis of a R245fa organic Rankine cycle (ORC) with different kinds of heat sources at evaporator [J]. Case Studies in Thermal Engineering, 2019, 13: 100385.
[7] PILI R, ROMAGNOLI A, SPLIETHOFF H, WIELAND C. Techno-economic analysis of waste heat recovery with ORC from fluctuating industrial sources [J]. Energy Procedia, 2017, 129: 503-510.
[8] CAVAZZINI G, dal TOSO P. Techno-economic feasibility study of the integration of a commercial small-scale ORC in a real case study [J]. Energy Conversion and Management, 2015, 99: 161-175.
[9] LI Gang. Organic Rankine cycle performance evaluation and thermoeconomic assessment with various applications part I: Energy and exergy performance evaluation [J]. Renewable and Sustainable Energy Reviews, 2016, 53: 477-499.
[10] LI Gang. Organic Rankine cycle performance evaluation and thermoeconomic assessment with various applications part II: economic assessment aspect [J]. Renewable and Sustainable Energy Reviews, 2016, 64: 490-505.
[11] SUN Fa-ming, IKEGAMI Y, JIA B, ARIMA H. Optimization design and exergy analysis of organic Rankine cycle in ocean thermal energy conversion [J]. Applied Ocean Research, 2012, 35: 38-46.
[12] USTAOGLU A, ALPTEKIN M, AKAY M E. Thermal and exergetic approach to wet type rotary kiln process and evaluation of waste heat powered ORC (Organic Rankine cycle) [J]. Applied Thermal Engineering, 2017, 112: 281-295.
[13] NI Jia-xin, ZHAO Li, ZHANG Zheng-tao, ZHANG Ying, ZHANG Jian-yuan, DENG Shuai, MA Ming-lu. Dynamic performance investigation of organic Rankine cycle driven by solar energy under cloudy condition [J]. Energy, 2018, 147: 122-141.
[14] TAFONE A, BORRI E, COMODI G, van den BROEK M, ROMAGNOLI A. Preliminary assessment of waste heat recovery solution (ORC) to enhance the performance of liquid air energy storage system [J]. Energy Procedia, 2017, 142: 3609-3616.
[15] BINA S M, JALILINASRABADY S, FUJII H. Energy, economic and environmental (3E) aspects of internal heat exchanger for ORC geothermal power plants [J]. Energy, 2017, 140: 1096-1106.
[16] van ERDEWEGHE S, van BAEL J, LAENEN B, D'HAESELEER W. Feasibility study of a low-temperature geothermal power plant for multiple economic scenarios [J]. Energy, 2018, 155: 1004-1012.
[17] BIANCHI M, BRANCHINI L, de PASCALE A, MELINO F, OTTAVIANO S, PERETTO A, TORRICELLI N, ZAMPIERI G. Performance and operation of micro-ORC energy system using geothermal heat source [J]. Energy Procedia, 2018, 148: 384-391.
[18] MAGO P J, SRINIVASAN K K, CHAMRA L M, SOMAYAJI C. An examination of exergy destruction in organic Rankine cycles [J]. International Journal of Energy Research, 2008, 32(10): 926-938.
[19] MAGO P J, CHAMRA L M, SRINIVASAN K, SOMAYAJI C. An examination of regenerative organic Rankine cycles using dry fluids [J]. Applied Thermal Engineering, 2008, 28(8, 9): 998-1007.
[20] TCHANCHE B F, LAMBRINOS G, FRANGOUDAKIS A, PAPADAKIS G. Exergy analysis of micro-organic Rankine power cycles for a small scale solar driven reverse osmosis desalination system [J]. Applied Energy, 2010, 87(4): 1295-1306.
[21] LI Tai-lu, ZHANG Zhi-gang, LU Jian, YANG Jun-lan, HU Yu-jie. Two-stage evaporation strategy to improve system performance for organic Rankine cycle [J]. Applied Energy, 2015, 150: 323-334.
[22] LI Tai-lu, YUAN Zhen-he, LI Wei, YANG Jun-lan, ZHU Jia-ling. Strengthening mechanisms of two-stage evaporation strategy on system performance for organic Rankine cycle [J]. Energy, 2016, 101: 532-540.
[23] WANG Zhi-qi, ZHOU Qi-yu, XIA Xiao-xia, LIU Bin, ZHANG Xin. Performance comparison and analysis of a combined power and cooling system based on organic Rankine cycle [J]. Journal of Central South University, 2017, 24(2): 353-359.
[24] THIERRY D M, FLORES-TLACUAHUAC A, GROSSMANN I E. Simultaneous optimal design of multi- stage organic Rankine cycles and working fluid mixtures for low-temperature heat sources [J]. Computers & Chemical Engineering, 2016, 89: 106-126.
[25] SALEH B, KOGLBAUER G, WENDLAND M, FISCHER J. Working fluids for low-temperature organic Rankine cycles [J]. Energy, 2007, 32(7): 1210-1221.
[26] LI Gang. Organic Rankine cycle environmental impact investigation under various working fluids and heat domains concerning refrigerant leakage rates [J]. International Journal of Environmental Science and Technology, 2019, 16(1): 431-450.
[27] LI Tai-lu, ZHU Jia-ling, ZHANG Wei. Performance analysis and improvement of geothermal binary cycle power plant in oilfield [J]. Journal of Central South University, 2013, 20(2): 457-465.
[28] ALJUNDI I H. Effect of dry hydrocarbons and critical point temperature on the efficiencies of organic Rankine cycle [J]. Renewable Energy, 2011, 36(4): 1196-1202.
[29] YARI M. Performance analysis of the different organic Rankine cycles (ORCs) using dry fluids [J]. International Journal of Exergy, 2009, 6(3): 323-342.
[30] XU Peng, LU Jian, LI Tai-lu, ZHU Jia-ling. Thermodynamic optimization and fluid selection of organic Rankine cycle driven by a latent heat source [J]. Journal of Central South University, 2017, 24(12): 2829-2841.
[31] LIU Qiang, SHEN Ai-jing, DUAN Yuan-yuan. Parametric optimization and performance analyses of geothermal organic Rankine cycles using R600a/R601a mixtures as working fluids [J]. Applied Energy, 2015, 148: 410-420.
[32] LIU Qiang, DUAN Yuan-yuan, YANG Zhen. Effect of condensation temperature glide on the performance of organic Rankine cycles with zeotropic mixture working fluids [J]. Applied Energy, 2014, 115: 394-404.
[33] HU Kai-yong, ZHU Jia-ling, LI Tai-lu, ZHANG Wei. Experimental investigation on characteristics of evaporator vaporization and pressure drops in an Organic Rankine Cycle (ORC) [J]. Energy Procedia, 2015, 75: 1631-1638.
[34] SUN Jie, LIU Qiang, DUAN Yuan-yuan. Effects of evaporator pinch point temperature difference on thermo- economic performance of geothermal organic Rankine cycle systems [J]. Geothermics, 2018, 75: 249-258.
[35] OZDIL N F T, SEGMEN M R, TANTEKIN A. Thermodynamic analysis of an Organic Rankine Cycle (ORC) based on industrial data [J]. Applied Thermal Engineering, 2015, 91: 43-52.
[36] ZHAO Meng, WEI Ming-shan, SONG Pan-pan, LIU Zhen, WANG Zhi-xiang. Effects of the ORC operating conditions on the engine performance for an Engine-ORC combined system [J]. Energy Procedia, 2017, 105: 662-667.
[37] XU Rong-ji, HE Ya-Ling. A vapor injector-based novel regenerative organic Rankine cycle [J]. Applied Thermal Engineering, 2011, 31(6, 7): 1238-1243.
(Edited by FANG Jing-hua)
中文导读
蒸发与冷凝耦合效应对有机朗肯循环地热发电性能的提高
摘要:有机朗肯循环(ORC)被广泛应用于低品位地热发电中,但是由于冷凝器和蒸发器中的热源/散热器与工质的匹配性差导致了大量的不可逆损失,严重影响了系统的技术经济性能。并且冷凝温度,冷却水温差,窄点温差通常根据工程经验被设为固定值。为了将ORC系统进行全面系统的优化,本文提出了蒸发冷凝过程的耦合效应,基于热力学定律,采用能量分析,火用分析和熵分析对温度为120 °C的地热水作为热源,异丁烷作为工作流体的ORC性能各项参数进行优化研究。结果表明,存在一组最佳蒸发温度和冷凝温度使系统性能得到最大限度地提高;净功率输出和系统综合性能在相同蒸发温度下达到最佳值,但系统达到最佳综合性能时对应的冷凝温度要低于达到最佳净输出功率时所对应的冷凝温度。
关键词:有机朗肯循环;地热发电;蒸发冷凝耦合效应;火用分析
Foundation item: Project(2018YFB1501805) supported by the National Key Research and Development Program of China; Project(51406130) supported by the National Natural Science Foundation of China; Project(201604-504) supported by the Key Laboratory of Efficient Utilization of Low and Medium Grade Energy (Tianjin University), China
Received date: 2018-10-24; Accepted date: 2019-01-31
Corresponding author: LI Tai-lu, PhD, Associate Professor; Tel: +86-22-60435787; E-mail: litailu19821028@163.com; ORCID: 0000- 0001-5458-3078

