J. Cent. South Univ. (2012) 19: 1909-1920 

DOI: 10.1007/s11771-012-1225-9

Local adaptive transmit power assignment strategy for wireless sensor networks

ZHAO Xue-jian(赵学健)¹, ZHUANG Yi(庄毅)², WANG Jin(王进)³

1. College of Internet of Things, Nanjing University of Posts and Telecommunications, Nanjing 210003, China;

2. College of Computer Science and Technology,

Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;

3. College of Computer and Software, Nanjing University of Information Science and Technology,Nanjing 210044, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: A distributed local adaptive transmit power assignment (LA-TPA) strategy was proposed to construct a topology with better performance according to the environment and application scenario and prolong the network lifetime. It takes the path loss exponent and the energy control coefficient into consideration with the aim to accentuate the minimum covering district of each node more accurately and precisely according to various network application scenarios. Besides, a self-healing scheme that enhances the robustness of the network was provided. It makes the topology tolerate more dead nodes than existing algorithms. Simulation was done under OMNeT++ platform and the results show that the LA-TPA strategy is more effective in constructing a well-performance network topology based on various application scenarios and can prolong the network lifetime significantly.

Key words: wireless sensor network; topology control; transmit power assignment; range assignment; path loss exponent; energy control coefficient; robustness; network lifetime

1 Introduction

In recent years, the availability of sensor nodes that are smaller, cheaper and more intelligent has enabled the deployment of densely distributed wireless sensor networks (WSNs) for a wide range of applications such as remote environmental monitoring, disaster surveillance, target tracking, healthcare and smart home [1-2]. Sensor nodes are resource stressed units, which means computation capability, storage capacity, communication range and available energy are limited [3].

As far, different techniques have been suggested to address the scarce resource problem, ranging from efficient hardware design [4] to appropriate placing of communicating nodes in the networks [5]. One of the most well-known approaches to this problem, which has been a subject of intensive research in recent years, is called topology control (TC). Most TC algorithms aim at building a reduced topology that will save energy while preserving network connectivity and area coverage [6]. Accordingly, the sparser the reduced topology is, the better the algorithm is. However, energy-efficient is not always the primary metric for all application domains. For instance, in body sensor networks (BSNs) used for human health monitoring, the critical data must be sent to control nodes in time. Otherwise, the patient may be delayed to be cured. Therefore, delay has become the primary metric in BSNs. Besides, if the topology is too sparse, there is a danger of network partitioning and high end-to-end delays.

In order to effectively alleviate the problems mentioned above, a distributed local adaptive transmit power assignment (LA-TPA) strategy is proposed. LA-TPA strategy consists of a target topology construction phase and a self-healing phase which are designed according to the characteristics of working progress of WSNs. The target topology construction phase is designed to construct a topology with better performance according to the environment and application scenario after the deployment of the network. The self-healing phase is designed to adjust the network topology adaptively in order to prolong the network lifetime when some nodes exhaust their energy or a fresh batch of nodes is deployed.

2 Related work

Power control algorithms can be classified into two categories: Homogeneous critical transmitting range (CTR) and non-homogeneous range assignment (RA). In the former case, all the nodes must use the same transmit power; in non-homogeneous TC algorithms, nodes are allowed to choose different transmit powers. PENROSE [7-8] proved that the CTR for connectivity equals the length of the longest edge of the Euclidean minimum spanning tree (EMST) and gives the CTR for connectivity in two- and three-dimensional networks in case of arbitrary node distribution and normal node distribution. SANTI and BLOUGH [9] reported the values of the CTR for connectivity by simulation. When the transmitting range is set to the CTR, the probability of generating a connected graph equals 0.99. In Ref. [10], the RA problem was firstly studied and the optimal solution to the RA problem which can be found in polynomial time in one-dimensional case is proposed. CLEMENTI et al [11] proved that the problem remains NP-hard in case of two-dimensional networks. Later on, the NP-hardness of finding the optimal solution to RA in three-dimensional networks has been proved in Ref. [10]. In recent years, the growing importance of TC has inspired some efforts to study the power control techniques. ALTHAUS et al [12] presented an exact branch and cut algorithm for solving weak symmetric version of RA problem based on an integer linear program formulation. In Ref. [13], LI et al introduced the local minimum spanning tree (LMST) protocol which is composed of three phases: Information exchange, topology construction and determination of transmit power. In Ref. [14], a fault-tolerant local spanning subgraph (FLSS) protocol is presented. LI and HOU [14] proved that FLSS preserves k-connectivity, and it minimizes the transmitting range of nodes in the network over all localized algorithms. In cone-based topology control (CBTC) protocol [15], a node must retain connections to at least one neighbor in every direction, where parameter ρ determines the granularity of every direction. In Ref. [16], the DistRNG protocol was proposed, and it is a distributed implementation of the computation of the relative neighborhood graph (RNG). In Ref. [17], a lightweight neighbor-based TC algorithm called XTC was presented. This algorithm computes a topology that contains only bidirectional links and preserves worst-case connectivity. In Ref. [18], solutions were proposed for the k-fault tolerant power assignment problem such that the total power consumption is minimized and any pairwise sensor node is k-vertex connected. INDRANIL et al [19] presented a distributed algorithm for assigning minimum possible power to all the nodes in static wireless sensor networks and extended the algorithm to networks having mobile nodes. In Ref. [20], ANEJA et al studied the strong minimum energy topology design problem in wireless sensor networks to assign transmission power to each sensor node such that the induced directed graph topology is strongly connected and the total energy consumption is minimized. In Ref. [21], LIU et al proposed a localized energy-efficient topology control algorithm for wireless sensor networks with power control capability in network nodes in order to prolong network lifetime. In Ref. [22], LI et al proposed three heuristics to adjust the limited transmission power for each sensor node to find a power assignment to reserve strong connectivity and achieve minimum energy cost in wireless sensor networks. In Ref. [23], a simple distributed topology control algorithm named step topology control (STC) was proposed. In STC, a node u removes the edge (u, v) if and only if there is a path with three or fewer hops between node u and node v. The algorithm which reduces energy consumption while preserving the connectivity can reduce energy cost by adjusting the power level.

Although there are many power control algorithms used for TC, designing a robust TC algorithm suitable for various application scenarios is still a challenging issue. Consequently, a distributed local adaptive power control algorithm used for TC is proposed in this work. Our contribution lies in the following three aspects. Firstly, the impact of path loss exponent α and energy control coefficient λ on the minimum covering district is analyzed. Thus, path loss exponent of the environment is introduced to characterize the minimum covering district more accurately. And energy control coefficient is introduced to characterize the minimum covering district properly according to the application scenario. Secondly, a topology maintenance scheme is proposed in LA-TPA algorithm by adjusting the energy control coefficient adaptively. Thirdly, LA-TPA strategy is described in detail and properties of LA-TPA are proved. Besides, the performance of LA-TPA strategy is verified by simulations results.

3 Preliminaries and basic idea

For the sake of convenience, the preliminary definitions and basic idea of LA-TPA strategy will be described. Firstly, some reasonable assumptions are given as follows:

1) Sensor nodes are uniformly and randomly distributed in a rectangle district;

2) Locations are available to the nodes;

3) All sensor nodes have the same maximum transmit power p_max and all sensor nodes can adjust the transmit power continuously;

4) The pass loss exponent is a constant decided by the environment after the deployment of the sensor nodes;

5) The network is well connected if all sensor nodes use maximum transmit power.

3.1 Preliminary definitions

In this work, the network topology is represented by a graph G=(V(G), E(G)), where V(G) and E(G) are the node set and edge set, respectively.

Definition 1: Transmit power assignment problem

N nodes are randomly distributed in a rectangle district. Transmit power assignment problem is to determine the transmit power p_i (i∈[1, N]) for every node adaptively to maintain the network connected for a long time to the fullest extent while some network performance metrics like network capacity and latency are met.

Definition 2: Original topology graph (G_o)

When all the nodes in the network use the maximum transmit power, the network topology is called original topology graph.

Definition 3: Target topology graph (G_t)

When each node in the network is assigned a proper transmit power by a specific algorithm, the network topology is called target topology graph. Target topology graph is represented by G with the algorithm name as a subscript.

Definition 4: Physical neighbor set (N_p(u))

Definition 5: Logical neighbor set (N_L(u))

Definition 6: Relay node set (R(u, v))

For a particular algorithm, R(u, v)=N_L(u)∪N_L(v).

Definition 7: Relay district (D(u, v))

Relay district is the minimum area that can cover all the nodes in R(u, v).

Definition 8: Minimum covering district (D_min(u))

According to a particular algorithm, for , if the path from node u to node v is, and , …, , then the district that just can cover all the second nodes on the paths is called minimum covering district of node u.

3.2 Basic idea

WSNs usually reveal the presence of several distinct phases with particular characteristics: The birth phase, the working life phase and the death phase. The birth phase corresponds to the progressive arrival of nodes during the network deployment. Each node diffuses “Hello” message to indicate its presence and then a logical structure is established according to a self-organization scheme in this phase. The phase of working life begins as soon as the logical structure is stabilized and finishes when there are too many modifications in the network due to a new massive deployment of nodes or because of the death of nodes. The last phase then begins until the network cannot function properly.

The goal of TC is not only to construct a target topology with better performance according to the environment and the application scenario after the birth phase but also to maintain the network function properly as long as possible with desired property when a few of nodes exhaust their energy or new nodes are deployed during the working life phase.

What is a target topology with better performance? SANTI [24] has concluded from the energy consumption and the network capacity point of view that, it is better to communicate using short, multi-hop paths between the sender and destination. This means that minimizing the transmit power of the nodes is an effective manner to reduce energy consumption and increase network capacity. As shown in Fig. 1, node v is a physical neighbor of node u. And nodes w₁, w_i (2≤i≤m), v are in the minimum covering district of node u, w_i-1(2≤i≤m), w_m, respectively. Then, it is more energy-efficient and capacity-efficient for node u to transmit a packet to node v through the path (u, w₁, w₂, …, w_m, v) (m≥0) than to transmit a packet directly. However, in different application scenarios, energy and capacity are not always the primary metrics. Consequently, transmit power assignment, i.e. determining the minimum covering district with desired property for each node is the first problem that must be tacked by LA-TPA strategy.

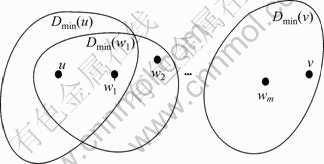
Fig. 1 Minimum covering district

The other problem that must be handled by LA-TPA strategy is how to adjust the minimum covering district dynamically during the working life phase of WSNs. As shown in Fig. 2, the dashed circles centered by node u and node v are the minimum covering districts of node u and node v, respectively. And the solid circles centered by node u and node v are the maximum covering districts of node u and node v, respectively. The left cluster, the right cluster and the isolated node w₂ are connected by a relay node w₁ initially. When node w₁ is dead, in order to maintain the network function properly, the transmit power of node u and node v must increase adaptively to cover node w₂ as an intermediate node.

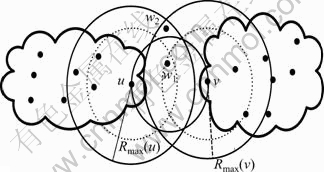
Fig. 2 Self-healing scheme of LA-TPA

In order to deal with the problems mentioned above, the Gabriel graph (GG) [25] model and relative neighborhood graph (RNG) model [26] are studied. In fact, GG model and RNG model are two special cases of β-Skeleton when the β values are 1 and 2, respectively. When GG model is used, the link between node u and node v will be pruned if there is a node w in the corresponding area of β-Skeleton (β=1). This means that the β-Skeleton area (β=1) is the relay district of (u, v). Similarly, when RNG model is used, the relay district of (u, v) becomes the β-Skeleton area (β=2). It can be seen that RNG model, GG model and their generalizations are all static models. They cannot construct better performance topologies for various applications. In order to construct a topology with better performance for a specific application, we must strike a balance between energy efficient and other performance metrics, such as delay and reliability.

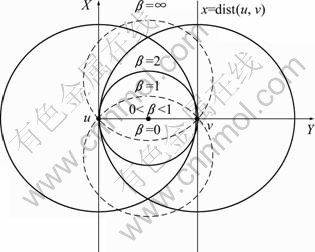
Fig. 3 β-Skeleton

4 LA-TPA strategy

The LA-TPA strategy is described in detail firstly. Then, the properties of LA-TPA strategy are proved. Finally, an analysis is given on the pass loss exponent α and energy control coefficient λ.

4.1 Description

LA-TPA strategy contains a target topology construction phase and a self-healing phase according to the characteristics of working progress of WSNs. The goal of target topology construction phase is a topology with better network performance according to the environment and the application scenario. The self-healing phase is designed to adjust the topology adaptively when some nodes exhaust their energy or new nodes are deployed.

The LA-TPA strategy works in a completely distributed manner. During the whole lifetime of the network, one of the functions of sink node is to start the topology algorithm by broadcasting a “Top” message. Another important function of sink node is to verify the desired network performance, such as delay. If the desired network performance metrics in specific application scenario are not satisfied, the sink node will adjust the topology in time by broadcasting a “Retop” message. The “Top” message should contain the initial path loss exponent and energy control coefficient and the adjustment of energy control coefficient is included in the “Retop” message. The pseudocode of the sink node is shown in Algorithm 1.

Algorithm 1: Target topology construction algorithm for sink node

For sensor nodes in the network, the operations are identical. In the topology construction phase, the algorithm should response to the following six events as Algorithm 2 shows. For the sake of simplicity, we take node u as an example.

1) Deployment finish event

When all the nodes are deployed, they will be initialized by a “Top” message from the sink node. Then, each node in the network, such as node u, will broadcast a “Hello” message using the maximum transmit power P_max. The node ID and location should be contained in the “Hello” message. As a result, the “Hello” message should be received successfully by all the nodes in N_p(u).

2) “Hello” message receive event

Upon receiving the “Hello” message from a neighbor node v, node u will compute W_u,v (energy consumption of the link) and store it in the memory. In addition, node v is inserted to  in ascending order of W to create a total order of all its physical neighbor nodes.

3) Neighbor discovery finish event

The neighbor discovery finish event is triggered by a preset timer D_t. When the timer expires, it means that the node has received the “Hello” messages from all its physical neighbors. Then, the node should broadcast the total order to all its physical neighbor nodes.

4) Total order receive event

Upon receiving the total order  from node v, node u will store it in the memory. When the node has received the total orders from all neighbor nodes, node u will select nodes from its physical neighbor set to form the logical neighbor set. For this purpose, node u traverses  in descending order. For example, when node v is considered, it will be included in N_L(u) if there is no node w meeting the following conditions:,  and  Otherwise, the node v will be included in N_L(u).

5) Target topology construction event

When the timer C_t represents the target topology construction event expires, node u will select a transmit power level which can just cover all the nodes in N_L(u).

6) Topology reconstruction event

Upon receiving a “Retop” message from the sink node, it means that the desired network performance is not satisfied. Consequently, the topology will be reconstructed until meeting the requirements.

Algorithm 2: Target topology construction algorithm for sensor nodes

Algorithm 3 presents the pseudocode of self-healing phase. In the self-healing phase, the nodes in the network just need to process the topology adjustment event represented by a self-message adjust. The topology adjustment event is usually caused by death of old nodes or deployment of fresh nodes. Sometimes, mobility of the nodes can lead to an adjustment of network topology too. When the topology adjustment event happens, the node should set a random back-off time t. If the node receives a “Connect” message before the back-off time expires, it accepts the connection invitation and then continues previous work. Otherwise, the node adjusts λ with a step of 0.1 and re-determines its logical neighbor set. This is repeated until the preset conditions are satisfied. Finally, the node broadcasts a “Connect” message to its logical neighbors.

Algorithm 3: Self-healing algorithm for sensor nodes

4.2 Properties

Theorem 1: Connectivity

The target topology G_LA-TPA is connected if and only if the original topology G_o is connected.

Proof: According to the definitions of target topology and original topology, G_o=(V_o, E_o), G_LA-TPA=(V_LA-TPA, E_LA-TPA) and V_o=V_LA-TPA, E_oE_LA-TPA. Consequently, if G_o is not connected, G_LA-TPA must be disconnected. In order to prove the sufficiency of this, we assume for contradiction that G_LA-TPA contains at least one pair of non-connected nodes which is connected in G_o. Without loss of generality, we assume (u, v) is the non-connected node pair with the minimum Euclidean distance. Obviously, the nodes u and v must be connected directly by edge (u, v) in G_o. However, they are disconnected in G_LA-TPA, i.e. v∈N_L(u). This means that when node v is considered by node u based on the LA-TPA strategy, there is a node w∈ and, i.e. node u and node w are connected by edge (u, w). Similarly, we can infer that node v and node w are also connected by edge (v, w). In conclusion, node u and node v are connected by node w, which contradicts with the assumption that node u and node v are not connected in G_LA-TPA.

Theorem 2: Symmetry

The edges in G_LA-TPA are symmetric, i.e. a node u includes node v in N_L(u) if and only if the node v includes node u in N_L(v).

Proof: Two assumptions are given beforehand. Assumption 1: ; Assumption 2: . On the basis of assumption 1, there must exist at least a node w∈ according to LA-TPA algorithm. Consequently, we can infer that node u belongs to , which contradicts with Assumption 2. The symmetry is derived.

Theorem 3: Planarity

When λ=1, G_LA-TPA is planar, i.e. it contains no two intersecting edges.

Proof: Suppose that for the sake of contradiction the two edges (u, v) and (w, x) intersect in G_LA-TPA. Consequently, at least one angel is no less than π/2 in quadrangle uwvx. Without loss of generality, let the angel adjacent to node u, i.e. Since, we can infer and .When node w is considered by node x, it will be included in N_L(x), which is a contradiction with the assumption that the edge (w, x) is in G_LA-TPA.

Theorem 4: Adaptivity

If there is no three nodes on a straight line, G_LA-TPA is the same as G_o when λ=2^1-α.

Proof: On the basis of previous analysis, if , the node w must be at the midpoint of (u, v). However, there is no three nodes lying on a straight line, thus for any pair of nodes in the network, for example (u, v), there is no node w satisfyingConsequently, according to the LA-TPA strategy, for  , i.e. . It is equivalent to .

Theorem 5: Bounded degree

If λ=2, G_LA-TPA has degree of at most 6, i.e. no two adjacent edges in G_LA-TPA enclose an angle less than π/3.

Proof: Assume for contradiction that there exist edges (u, v) and (u, w) enclosing an angle α<π/3 at node u in G_LA-TPA. Without loss of generality, let d(u, w)<  d(v, u), i.e., then the angle β at node w is bigger than the angle χ at node v. According to the fact that triangles always contain 180°, we can deduce that β>π/3. Consequently, β>α and d(u, w). Since λ=2, according to the algorithm, it follows that v includes u in, which contradicts with the assumption that the edge (u, v) is in G_LA-TPA.

Theorem 6: Sparseness

If λ₁<λ₂, G_LA-TPA(λ₂) is more sparse than G_LA-TPA(λ₁), i.e. E(G_LA-TPA(λ₂))E(G_LA-TPA(λ₁)).

Proof: Suppose that for the sake of contradiction there is an edge (u, v)∈E(G_LA-TPA(λ₂) but not included in E(G_LA-TPA(λ₁)). Then, according to the LA-TPA algorithm, there must be a node w satisfying and , then we can deduce that  . It contradicts with the condition  of the theorem.

Corollary 1: For  in the network, the relay district is  for LA-TPA1, and the relay district is for LA-TPA2. If then.

Proof: Forin the network, if there is a node w in satisfying the conditions of LA-TPA algorithm, it is in  undoubtedly. Consequently, if the edge (u, v) is pruned in LA-TPA1, it must be pruned in LA-TPA2, too. On the contrary, if there is a node w in satisfying the conditions of LA-TPA algorithm, it is not always in  undoubtedly. That is to say, if the edge is pruned in LA-TPA2, it can be preserved in LA-TPA1. In conclusion, we can prove that.

4.3 Parameter analysis

WSNs usually work in distinct environments, such as forests, plains and downtown areas with a path loss exponent varying from 1.6 to 6 [1]. The impact of pass loss exponent on the relay district is shown in Fig. 4. Suppose that node u and node v are placed at (0, 0) and (2, 0), respectively, and the relay district D(u, v) of α in the first quadrant is the area surrounded by the corresponding curve and X-axis. We can see that the relay district D(u, v) increases with the path loss exponent α. This means that the path loss exponent α has an influence on the target topology according to Corollary 1. Consequently, in order to characterize the relay district and minimum covering district more accurately and precisely, pass loss exponent of the environment should be tested previously and assigned to every node in an offline way.

Fig. 4 Impact of pass loss exponent α on relay district

Figure 5 describes the impact of energy control coefficient λ on the relay district (the pass loss exponent α is set to be 2). Similarly, suppose that node u and node v are placed at (0, 0) and (2, 0), respectively, and the relay district D(u, v) of λ in the first quadrant is the area surrounded by the corresponding curve and X-axis. We can see that the relay district D(u, v) increases with the energy control coefficient λ. According to Theorem 6, in order to get a sparse network topology to reduce conflicts and increase network throughput, the energy control coefficient is the larger the better. However, the target topology also needs to meet other performance metrics, such as delay. Consequently, we should choice a proper energy control coefficient according to the application scenario. During the working life phase, when some nodes begin to die because of energy depletion or outside attacks, the energy control coefficient λ should decrease gradually in a distribute manner to maintain the network connected for a long time. On the contrary, when new nodes are detected, the energy control coefficient λ should be adjusted larger adaptively to pursue a topology with better network performance.

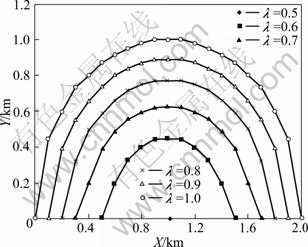
Fig. 5 Impact of energy control coefficient λ on relay district

The minimum value of λ is determined by the pass loss exponent. It is known by simple knowledge of geometry that the energy control coefficient λ will attain the minimum value if the relay node locates on the midpoint of the two communication nodes. And the minimum value of λ is . The maximum value of λ is 2 when node w is selected as a relay node of (u, v) and .

5 Simulation analysis

A series of experiments are carried out to evaluate the performance of LA-TPA algorithm on OMNeT++ platform. In all simulations, the nodes are randomly distributed in an 800 m×500 m rectangular area. The number of the sensor nodes varies from 50 to 100. The transmitting range of the sensor nodes corresponding to the maximum transmit power is 200 m when the pass loss exponent is 2.

As we know, topology control algorithms have an influence on the network throughput, interference, life cycle and some other indicators; however, these indicators are also concerned with routing protocols, MAC protocols and so on, which cannot be measured simply from the perspective of topology control. Consequently, the average node degree, the average local path hop and the average transmit power are used to evaluate the performance of the topology control algorithms. In fact, the average node degree is the average number of nodes in the logical neighbor set. It can reflect the severity of the signal conflict of the network, which has an influence on the throughput of the network. The average local path hop is the average hop count for a node to transmit a packet to the sink node (ID=0). It can not only reflect the energy consumption for a node to transmit a packet to the sink node, but also affects the transmit delay of the packet. It can be said that the topology with a smaller average local path hop has a better network performance. The average transmit power is vital for the energy efficiency and network capacity. It is measured by its corresponding transmit range in this work. In addition, all data displayed are averages of 100 repeated simulations.

5.1 Impact of pass loss exponent

In the first group of experiments, the impact of pass loss exponent in the LA-TPA algorithm is verified. The pass loss exponent is set to be 1.6, 2, 3, 4, 5 and 6 separately. The topologies constructed by the LA-TPA algorithm when there are 80 nodes in the rectangular area are shown in Fig. 6. It is known that the relay district becomes smaller and smaller when the pass loss exponent decreases. Thus, the topology constructed by the LA-TPA algorithm should be sparser and sparser according to Corollary 1. Figure 6 has proved this intuitively.

Figure 7 shows the impact of pass loss exponent on the average node degree, the average local path hop and the average transmit power. When the pass loss exponent varies from 1.6 to 6, the ranges of the average      node degree, the average local path hop and the average transmit power are [2.45, 4.23], [5.88, 9.39] and [75, 112], respectively, if there are 80 nodes in the rectangular area. Consequently, in order to characterize the relay district according to the real environment more accurately, the pass loss exponent should be tested in the real environment where the network will be deployed and assigned to every node in an offline way previously.

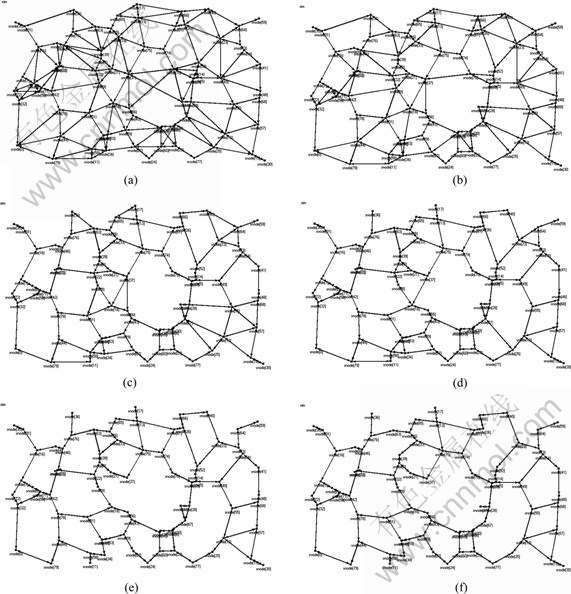
Fig. 6 Topologies constructed by LA-TPA strategy (α∈[1.6, 6], λ=1): (a) G_LA-TPA (α=1.6, λ=1); (b) G_LA-TPA (α=2, λ=1);           (c) G_LA-TPA (α=3, λ=1); (d) G_LA-TPA (α=4, λ=1); (e) G_LA-TPA (α=5, λ=1); (f) G_LA-TPA (α=6, λ=1)

5.2 Impact of energy control coefficient

Another group of experiments are carried out to test the role of energy control coefficient in the LA-TPA algorithm. In this group of experiments, the pass loss exponent is set to be 3 previously. And the energy control coefficient varies from 0.5 to 1.6. Figure 8 shows the topologies constructed by the LA-TPA algorithm when there are 80 nodes in the rectangular area. Similarly, the relay district becomes smaller and smaller when the energy control coefficient decreases. Consequently, the topology constructed by the LA-TPA algorithm should be denser and denser according to Corollary 1 when the energy control coefficient varies from 1.6 to 0.5.

Fig. 7 Impact of pass loss exponent: (a) On average node degree; (b) On average local path hop; (c) On average transmit power

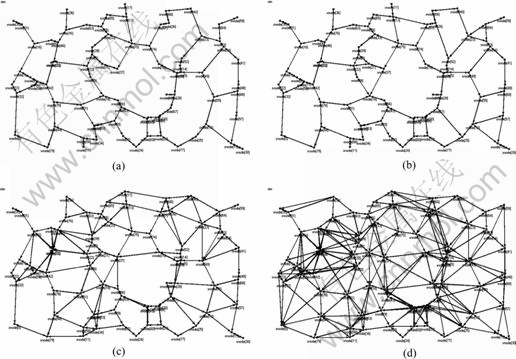
Fig. 8 Topologies constructed by LA-TPA strategy (α=3, λ∈[0.5, 2]): (a) G_LA-TPA (α=3, λ=1.6); (b) G_LA-TPA (α=3, λ=1.2);         (c) G_LA-TPA (α=3, λ=0.8); (d) G_LA-TPA (α=3, λ=0.5)

Figure 9 describes the influence of energy control coefficient when the number of nodes varies from 50 to 100. When the energy control coefficient varies from 0.5 to 1.6, the range of the average node degree, the average local path hop and the average transmit power are [2.4, 6.8], [4.31, 9.38] and [75.27, 143.8], respectively, if there are 80 nodes in the rectangular area. In contrast with   Fig. 7, it can be seen that the influence of energy control coefficient is more significant than the influence of the pass loss exponent. Thus, in order to prolong the lifetime of the network, it is an effective way to adjust the energy control coefficient locally in a distributed way.

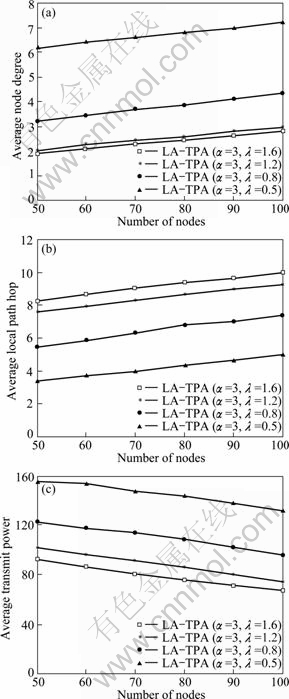
Fig. 9 Impact of energy control coefficient: (a) On average node degree; (b) On average local path hop; (c) On average transmit power

5.3 Comparison to other protocols

In order to demonstrate the performance of the proposed algorithm, a simulation-based comparative study of the LA-TPA, XTC and STC algorithms was conducted. STC algorithm is added as another comparison object here because it also takes the pass loss exponent into consideration. In this group of experiments, the pass loss exponent and the energy control coefficient are set to be 3 and 1.6 previously. Figure 10 shows    the target topologies constructed by the three algorithms mentioned above when there are 80 nodes in the rectangular area.

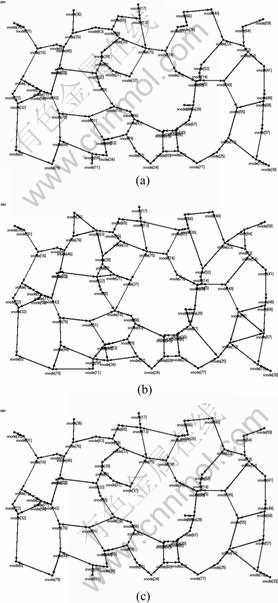
Fig. 10 Topologies constructed by LA-TPA strategy, XTC algorithm and STC algorithm: (a) G_LA-TPA (α=3, λ=1.6);     (b) G_XTC; (c) G_STC

Figure 11 shows the average node degree, the average local path hop and the average transmit power of the three algorithms mentioned above when the number of the nodes deployed in the rectangular area varies from 50 to 100. It can be seen that the performance metrics of the target topologies constructed by the three algorithms just have a small deviation. Consequently, in order to demonstrate the superiority of the proposed algorithm, a comparison of an additional significant performance metrics, that is, maximum number of death nodes, is given. In this group of experiments, one of the nodes in the network is killed per second. Therefore, the network will be disconnected sooner or later. The maximum number of death nodes is the threshold when the network becomes isolated just recently.

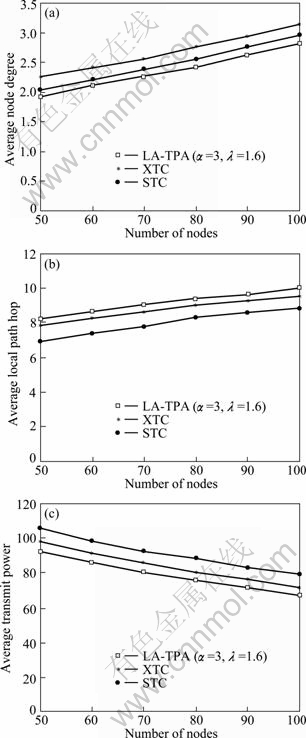
Fig. 11 Comparison of three algorithms: (a) Average node degree; (b) Average local path hop; (c) Average transmit power

The maximum number of dead nodes of the three algorithms is shown in Fig. 12. It can be seen that the LA-TPA algorithm can tolerate more death nodes than XTC and STC algorithms when the number of nodes in the network varies from 50 to 100. Moreover, the maximum number of dead nodes corresponding to the LA-TPA algorithm increases more sharply than the other two algorithms. The maximum number of dead nodes corresponding to the LA-TPA is about 60 when there are 100 nodes in the network, which is much larger than 20 and 18 corresponding to the STC and XTC, respectively. Consequently, it is believed that the LA-TPA can prolong the lifetime of the network effectively.

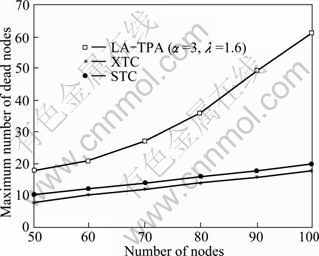
Fig. 12 Comparison of maximum number of dead nodes

6 Conclusions

1) The impact of path loss exponent and energy control coefficient on the minimum covering district is significant. Thus, a novel distributed local adaptive transmit power assignment strategy LA-TPA considering these two factors is proposed to construct topologies for various application scenarios. Simulation results show that the topologies constructed by the LA-TPA strategy can meet diverse performance metrics.

2) The energy control coefficient is still used to adjust the transmit power locally when a few of the nodes exhaust their energy or new nodes are deployed. Simulation results show that the proposed algorithm can attain a target topology as better as existing excellent topology algorithms, such as XTC and STC. More importantly, it can tolerate more dead nodes than these two algorithms. This means that it can prolong the lifetime of the network effectively.

References

[1] AKYILDIZ I F, SU W, SANKARASUBRAMANIAM Y, CAYIRCI E. Wireless sensor networks: A survey [J]. Computer Network, 2002, 38(4): 393-422.

[2] JENNIFER Y, BISWANATH M, DIPAK G. Wireless sensor network survey [J]. Computer Networks, 2008, 52(12): 2292-2330.

[3] SUNIL J, PRABHAT R. A Survey: Topology control for wireless sensor networks [C]// IEEE International Conference on Signal Processing, Communications and Networking. Chennai: IEEE Press, 2008: 422-427.

[4] HEMPSTEAD M, TRIPATHI N, MAURO P, WEI G Y, BROOKS D. An ultra low power system architecture for sensor network applications [C]// Proceeding of the 32nd International Symposium on Computer Architecture. Madison, WI: IEEE Computer Society Press, 2005: 208-219.

[5] LIU H, ROEDER T, WALSH K, BARR R, SIRER E G. Design and implementation of a single system image operating system for ad hoc networks [C]// 3rd International Conference on Mobile Systems, Applications, and Services. Seattle, WA: USENIX Association Press, 2005: 149-162.

[6] SAJJAD Z, AMIR N, NASSER Y. Efficient construction of network topology to conserve energy in wireless Ad hoc networks [J]. Computer Communications, 2008, 31(1): 160-173.

[7] PENROSE M D. A strong law for the longest edge of the minimal spanning tree [J]. The Annals of Applied Probability, 1999, 27(1): 340-361.

[8] PENROSE M D. On k-connectivity for a geometric random graph [J]. Random Structures and Algorithms, 1999, 15(2): 145-164.

[9] SANTI P, BLOUGH D M. The critical transmitting range for connectivity in sparse wireless ad hoc networks [J]. IEEE Transactions on Mobile Computing, 2005, 2(1): 25-39.

[10] KIROUSIS L, KRANAKIS E, KRIZANC D, PELC A. Power consumption in packet radio networks [J]. Theoretical Computer Science, 2000, 243(1/2): 289-305.

[11] CLEMENTI A, PENNA P, SILVESTRI R. Hardness results for the power range assignment problem in packet radio networks [C]// 2nd International Workshop on Approximation Algorithm for Combinatorial Optimization Problems (RANDO APPRO 99). Berkeley, CA: Springer Press, 1999: 197-208.

[12] ALTHAUS E, CALINESCU G,ANDOIU I, PRASAD S, TCHERVENSKI N, ELIKOVSKY A. Power efficient range assignment in ad hoc wireless networks [C]// IEEE WCNC2003. New Orleans, LA: IEEE Press, 2003: 1889-1894.

[13] LI N, HOU J C, SHA L. Design and analysis of an MST-based topology control algorithm [J]. IEEE Transactions on Wireless Communications, 2005, 4(3): 1195-1206.

[14] LI N, HOU J C. Flss: A fault-tolerant topology control algorithm for wireless networks [C]// Proc of the 10th Annual International Conference on Mobile Computing and Networking, MobiCom’04. New York: ACM Press, 2004: 275-286.

[15] LI N, HALPERN J Y, BAHL P. A cone-based distributed topology control algorithm for wireless multi-hop networks [J]. IEEE Transactions on Networking, 2005, 13(1): 147-159.

[16] BORBASH S A, JENNING E H. Distributed topology control algorithm for multihop wireless networks [C]// Proc IEEE International Joint Conference on Neural Networks. Honolulu, HI: IEEE Press, 2002: 355-360.

[17] ROGER W, AARON Z. XTC: A practical topology control algorithm for ad hoc and sensor networks [C]// 18th International Parallel and Distributed Processing Symposium. New Mexico, 2004: 216-223.

[18] LIU Li, LI Lian, HU Bin. Algorithms for k-fault tolerant power assignments in wireless sensor networks [J]. Science China Information Sciences, 2010, 53(12): 2527-2537.

[19] INDRANIL S, LOKESH K S, SUBHAS K G, RANJEET K P. Distributed fault-tolerant topology control in wireless multi-hop networks [J]. Wireless Networks, 2010, 16(6): 1511-1524.

[20] ANEJA Y P, CHANDRASEKARAN R, XIANGYONG L, NAIR K P K. A branch-and-cut algorithm for the strong minimum energy topology in wireless sensor networks [J]. European Journal of Operational Research, 2010, 204(3): 604-612.

[21] LIU Hai-tao, ZHANG Bao-xian, ZHENG Jun, HUSSEIN T M. An energy-efficient localized topology control algorithm for wireless ad hoc and sensor networks [J]. International Journal of Communication Systems, 2008, 21(11): 1205-1220.

[22] LI De-ying, DU Hong-wei, LIU Lin, HUANG S C. Joint topology control and power conservation for wireless sensor networks using transmit power adjustment [C]// 14th Annual International Conference on Computing and Combinatorics. Dalian, China: Springer Press, 2008: 541-550.

[23] HARISH S, THOMAS G. A new distributed topology control algorithm for wireless environments with non-uniform path loss and multipath propagation [J]. Ad hoc Networks, 2010, 8(3): 280-294.

[24] SANTI P. Topology control in wireless Ad hoc and sensor networks [J]. ACM Computing Surveys, 2005, 37(2): 164-194.

[25] NARAYANASWAMY S, KAWADIA V, SREENIVAS R S, KUMAR P R. Power control in ad hoc networks: Theory, architecture, algorithm and implementation of the COMPOW protocol [C]// Proc of the European Wireless Conf. Florence: Springer Press, 2002: 156-162.

[26] TOUSSAINT G T. The relative neighborhood graph of a finite planar set [J]. Pattern Recognition, 1980, 12(4): 261-268.

(Edited by YANG Bing)

Foundation item: Projects(61101104, 61100213) supported by the National Natural Science Foundation of China; Project(NY211050) supported by Fund of Nanjing University of Posts and Telecommunications, China

Received date: 2011-03-01; Accepted date: 2012-03-28

Corresponding author: ZHAO Xue-jian, PhD; Tel: +86-25-83192013; E-mail: zhaoxj@njupt.edu.cn